管道修复用涤纶/苎麻非织造复合材料拉伸强度

伏立松， 张淑洁， 王 瑞,2， 杨兆薇， 荆梦轲

(1. 天津工业大学 纺织科学与工程学院， 天津 300387；2. 天津工业大学 先进纺织复合材料教育部重点实验室， 天津 300387)

许多在役的大管径、非压力排污或排水管道因老化等因素会出现严重的裂缝、腐蚀穿孔、渗漏等受损现象，直接或间接地造成了巨大的经济损失[1]。为降低经济损失和保护水资源，迫切需要对受损的排水或排污管道进行修复。采用管状涤纶非织造复合材料作为内衬管的翻衬修复法具有不开挖、不影响交通、不破坏环境等优势[2]。目前，国内管状涤纶非织造复合材料翻衬修复受损排污或排水管道才刚刚起步，还没有相关的施工规范和工程质量验收标准。国外此方面的研究主要侧重于修复工艺、修复设备[3]，也制定出了一系列的标准可供参考，如ASTM F1743-17《采用现场固化热固性树脂管 (CIPP) 的现场拉制装置修复现有管线和管道的标准实施规程》、ASTM F1216-16《通过树脂浸渍管的倒置和硫化修复现有管线和管道的标准规程》等，但较少从理论上对管状涤纶非织造复合材料进行系统的设计与研究。

近几十年，石油资源的日益枯竭使得合成纤维的价格不断上涨，人们迫切地需要用天然纤维来部分取代或完全取代合成纤维[4]。其中，苎麻纤维具有高比强度和高比模量等性能，能够携带更多的树脂与旧管内壁黏接，与树脂结合的界面性能相比纯涤纶非织造材料有所改善[5]，因此有相关学者制备了涤纶/苎麻复合材料用于非开挖修复受损的管道。闫丹等[6]采用三因素回归旋转设计方法制备涤纶/苎麻非织造复合材料，对比了实际制备与混杂理论下的涤纶/苎麻非织造复合材料的拉伸强度，发现实际拉伸强度与理论拉伸强度存在较大的误差。罗凯等[7-8]对修复管径较小的燃气、给水等压力管道的涤纶/苎麻机织物复合材料进行微观形貌、接触角、纤维抽拔、黏结强度等研究，发现涤纶/苎麻机织物复合材料在翻衬施工中可以携带更多树脂与管壁黏合，解决管道内壁塌陷的问题。以上研究偏重于混杂纤维复合材料的性能特点，很少讨论纤维混杂设计对涤纶/苎麻复合材料的拉伸强度产生的影响。

针对这些问题，本文利用复合材料混合定律和胡克定律建立了涤纶/苎麻非织造复合材料的理论临界体积分数和拉伸强度的计算公式，制备了不同体积分数的涤纶/苎麻非织造复合材料，对其拉伸强度进行测试，得到临界体积分数与拉伸强度的实验值，找出与理论临界体积分数及理论拉伸强度的相关性，从而证明涤纶/苎麻非织造复合材料的理论临界体积分数和拉伸强度计算公式的可靠性，为翻衬修复排污或排水管道的管状混杂纤维非织造复合材料的强度设计提供理论方法。

1 混杂理论

1.1 理论临界体积分数

将涤纶与苎麻混杂制成的非织造复合材料简化成为单层复合材料板问题，如图1所示。

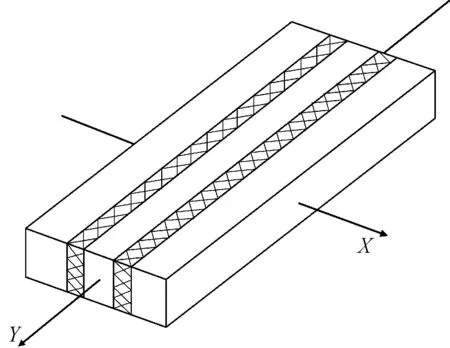
图1 单层复合材料板模型Fig.1 single-layer composite board model

根据复合材料的混合定律[9]可知，复合材料的拉伸强度：

σcu=σfVf+σmVm

(1)

(2)

式中：Vf为纤维体积分数，%；Vm为基体体积分数(基体的体积分数为Vm=1-Vf)，%；σcu为复合材料拉伸强度，MPa；σf为纤维拉伸强度，MPa；σm为基体拉伸强度，MPa，λ为基体体积含量，%。

涤纶/苎麻非织造复合材料的强度设计要满足管道工作内压引起的纵、横向应力[10]。

(3)

(4)

式中：σj、σw为涤纶/苎麻非织造复合材料的纵、横向应力，MPa；P为管道工作内压，MPa；D为管道内径，mm；h为管道壁厚，mm。

设单向涤纶/苎麻非织造复合材料板宽度为单位1，涤纶与苎麻纤维层的纤维网厚度为d1、d2，基体厚度为dm，基体厚度dm与纤维体积分数有关，则有：

(5)

式中，V1为涤纶层占纤维层总体积的体积分数，%。

结合式(2)和(5)，涤纶、苎麻纤维层的纤维网厚度与基体厚度的关系为

dm=λ(d1+d2)

(6)

涤纶/苎麻非织造复合材料沿纤维方向Y单向拉伸，在拉伸载荷F作用下发生断裂，得其平衡方程：

F=σ1d1×1+σ2d2×1+σmdm×1

(7)

式中：σ1为涤纶层拉伸应力，MPa；σ2为苎麻纤维层拉伸应力，MPa。

由胡克定律[9]得涤纶/苎麻非织造复合材料拉伸断裂应变[10]ε：

σ1=E1εσ2=E2εσm=Emε

(8)

式中：E1为涤纶层拉伸模量，MPa；E2为苎麻纤维层拉伸模量，MPa；Em为基体拉伸模量，MPa。

结合式(7)和(8)，推导出涤纶、苎麻纤维层的拉伸应力：

(9)

设涤纶纤维层、苎麻纤维层、基体的断裂应变分别为ε1a、ε2a和εma，且满足：ε1a<ε2a<εma，若当拉伸载荷F增加到Fa时，涤纶层首先断裂，即当F=Fa时，ε1=ε1a，σ1=σ1a，σ1a为涤纶层拉伸强度。根据式(9)，涤纶层断裂的平衡方程为

(10)

式中：涤纶层断裂后，苎麻纤维层和基体承担拉伸载荷Fa。此时涤纶/苎麻非织造复合材料的平衡方程为

Fa=σ2d2×1+σmdm×1

(11)

若在拉伸载荷Fa作用下，苎麻纤维层也到达断裂状态，即ε2=ε2a，σ2=σ2a，此时涤纶/苎麻非织造复合材料不会发生二次断裂。根据式(9)，苎麻纤维层断裂的平衡方程为

(12)

将式(6)代入式(10)和式(12)，涤纶、苎麻纤维层断裂的平衡方程为

(13)

翻衬修复受损大管径、非压力排污或排水管道的涤纶/苎麻非织造复合材料不允许发生二次断裂[11-12]。根据式(13)，涤纶/苎麻非织造复合材料不发生二次断裂的临界体积分数V1*为

(14)

1.2 理论拉伸强度

翻衬修复受损大管径、非压力排污或排水管道的涤纶/苎麻非织造复合材料的拉伸断裂情况可分为2种[6, 11]:

(15)

结合式(2)、(6)和式(15)，推导出简化后的涤纶/苎麻非织造复合材料拉伸强度：

(16)

(17)

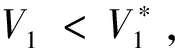
(18)

2 实验部分

2.1 实验材料及设备

实验材料：苎麻纤维规格为 6.3 dtex×90 mm(安徽雨燕麻业有限公司)；涤纶规格为 1.56 dtex×38 mm(天津利尔达化纤制品厂)；R400-2 内衬环氧树脂(天津合成材料工业研究所有限公司)，路博润 58887 热塑性聚氨酯(苏州希珍塑化有限公司)。

实验设备：电子天平(瑞安市英衡电器有限公司)，YG141型织物厚度测试仪(深圳市海滨仪器有限公司)，XFH型小和毛机(青岛市胶南针织机械厂)，CUARNICARD型罗拉式梳理机(西班牙SABADELL)，SCZ-1150型针刺机(常熟无纺机械设备厂)，Y/TD71-45 A 型塑料制品液压机(天津市液压厂)，INSTRON 5969型万能强力机(美国INSTRON)，Hitachi TM3030型台式扫描电镜(日本日立公司)。

2.2 涤纶/苎麻非织造复合材料的制备

涤纶与苎麻纤维以0、10%、20%、30%、40%、60%、80%、100%的体积分数混杂[13]，在小和毛机上混和开松，梳理机上成网，针刺机上以定量 600 g/m2、针刺密度为240刺/cm2的条件针刺，制成涤纶/苎麻非织造材料。温度180 ℃，压力4～6 MPa下液压机熔融聚氨酯，压力0.8～1.2 MPa下与涤纶/苎麻非织造材料复合16～20 s。定量 1 500 g/m2的环氧树脂来手糊覆膜后的涤纶/苎麻非织造材料，于室温下固化，制成涤纶/苎麻非织造复合材料。

2.3 测试方法

2.3.1 拉伸性能测试

为翻衬修复受损的大管径、非压力排污或排水管道，选用高强度、高模量的涤纶、苎麻纤维。参考ASTM D3379-75《高模量单丝材料拉伸强度和弹性模量测试方法》测试涤纶、苎麻纤维的拉伸强度和拉伸模量。随机地在纤维束上截取一段，抽出单根纤维，施加一定的张力，使单根纤维横向拉直紧绷在纸框上，单根纤维的两端用胶黏剂粘好，干燥后将纸框垂直固定于万能强力仪的上下夹具中，调试好仪器，剪断纸框；单根纤维的测定长度为20 mm，拉伸速度为10 mm/min；测试30组，取平均值，为涤纶、苎麻纤维的拉伸强度和拉伸模量。

按照GB/T 1447—2005《纤维增强塑料拉伸性能试验方法》测试涤纶/苎麻非织造复合材料的拉伸强度。拉伸试样规格约为250 mm×25 mm(长×宽)，纵横向各5个；采用美国INSTRON生产的万能强力仪进行测试，拉伸试样夹持距为150 mm，加载速度为5 mm/min。

2.3.2 形貌观察

采用Hitachi TM3030型台式扫描电镜，观察涤纶/苎麻非织造复合材料的纵横向断裂面微观形貌。

3 结果与讨论

3.1 理论临界体积分数

由于非织造材料的纤维取向多元，混杂效应的随机性比较大[14-15]，则采用单根涤纶、苎麻纤维的拉伸强度和拉伸模量模拟涤纶、苎麻纤维层的拉伸强度和拉伸模量，得到涤纶与苎麻纤维的临界体积分数和涤纶/苎麻非织造复合材料的理论拉伸性能的变化规律。测试并计算后得到的涤纶拉伸强度σ1a为0.63 GPa，拉伸模量E1为 13.17 GPa；苎麻纤维的拉伸强度σ2a为0.48 GPa，拉伸模量E2为7.86 GPa；环氧树脂的拉伸模量Em为2.96 GPa。假设纤维总体积含量Vf为0.6[13]，将以上数据代入式(14)中，通过计算可得高强涤纶与苎麻纤维的临界体积分数为17.7%。根据式(16)～(18)可知，当高强涤纶体积分数不低于17.7%时，此时翻衬修复受损大管径、非压力排污或排水管道的涤纶/苎麻非织造复合材料理论上不发生二次断裂。

3.2 理论拉伸强度

根据上述的高强涤纶与苎麻纤维的相关性能数据，结合式(16)～(18)，可得到不同涤纶纤维体积分数的涤纶/苎麻非织造复合材料的理论拉伸强度，如图2所示。

图2 不同涤纶体积分数的涤纶/苎麻非织造复合材料的理论拉伸强度Fig.2 Theoretical tensile strength of polyester/ramie nonwoven composites with different volume fractions of polyester fiber

从图2中可看出，涤纶/苎麻非织造复合材料的理论拉伸强度与涤纶纤维体积分数呈线性关系。当涤纶体积分数小于17.7%时，涤纶/苎麻非织造复合材料的理论拉伸强度随着涤纶体积分数的增加而降低；当涤纶体积分数大于17.7%，涤纶/苎麻非织造复合材料的理论拉伸强度随着涤纶体积分数的增加而增大；当涤纶体积分数等于17.7%，涤纶/苎麻非织造复合材料的理论拉伸强度最小。

3.3 结果验证

3.3.1 涤纶/苎麻非织造复合材料拉伸强度

表1示出不同涤纶体积分数的涤纶/苎麻非织造复合材料拉伸强度的测试结果。可知：涤纶体积分数为20%的涤纶/苎麻非织造复合材料的拉伸强度是涤纶体积分数为0、10%、20%、30%、40%、60%、80%和100% 8个组别中的最小值，为42.69 MPa，从而表明临界体积分数在涤纶体积分数20%附近。实验得到的临界体积分数在20%附近，与理论的临界体积分数17.7%区别不大。结果表明，建立的新型涤纶/苎麻非织造复合材料临界体积分数的计算公式具有较高的实用性。

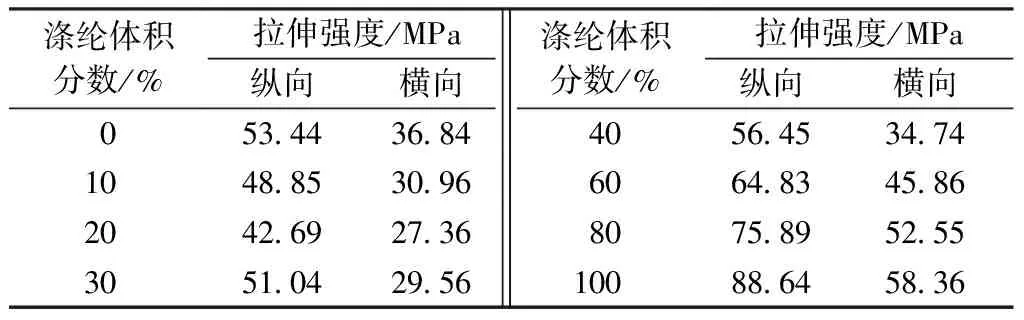
表1 不同涤纶体积分数的涤纶/苎麻非织造复合材料的拉伸强度Tab.1 Tensile strength of polyester/ramie nonwoven composites with different volume fractions of polyester fiber

3.3.2 实验值与理论值对比与分析

由表1发现：涤纶/苎麻非织造复合材料的实验拉伸强度与理论拉伸强度的变化规律一致，即涤纶纤维体积分数未到达临界体积分数时，涤纶/苎麻非织造复合材料的拉伸强度随涤纶体积分数的增加而减小，到达临界体积分数之后，随涤纶体积分数的增加而增大，与不同涤纶体积分数对涤纶/苎麻非织造复合材料的理论拉伸强度的影响结论相同。

与此同时发现，涤纶/苎麻非织造复合材料拉伸强度的实验值低于理论值。出现这一情况是因为在理论值计算当中将单根苎麻、涤纶的拉伸强度和拉伸模量模拟苎麻、涤纶层的拉伸强度和拉伸模量，未考虑苎麻、涤纶层的实际加工[16]。此外，树脂浸润纤维不全面也是导致同组其他涤纶/苎麻非织造复合材料的拉伸强度实验值低于理论值原因之一。

3.3.3 临界体积分数

为使翻衬修复受损大管径、非压力排污或排水管道的涤纶/苎麻非织造复合材料不发生二次断裂，进一步研究实验得到的临界体积分数，即涤纶体积分数约为20%。图3示出涤纶体积分数为20%附近的涤纶/苎麻非织造复合材料的拉伸强度。可知，涤纶体积分数为18%的涤纶/苎麻非织造复合材料的拉伸强度值最小，为41.57 MPa。涤纶体积分数为16%、18%、20%、22%和24%的5个组别中拉伸强度相差不大，表明临界体积分数在涤纶体积分数18%附近。同时考虑实际操作的便利，以及防止涤纶/苎麻非织造复合材料发生二次断裂现象，将临界体积分数设为涤纶体积分数20%更为合理。

图3 涤纶体积分数为20%附近的复合材料拉伸强度Fig.3 Tensile strength of composites near 20% of volume fraction of polyester fiber

3.4 复合材料的微观结构表征

图4示出涤纶/苎麻非织造复合材料的纵横向断裂面形貌。

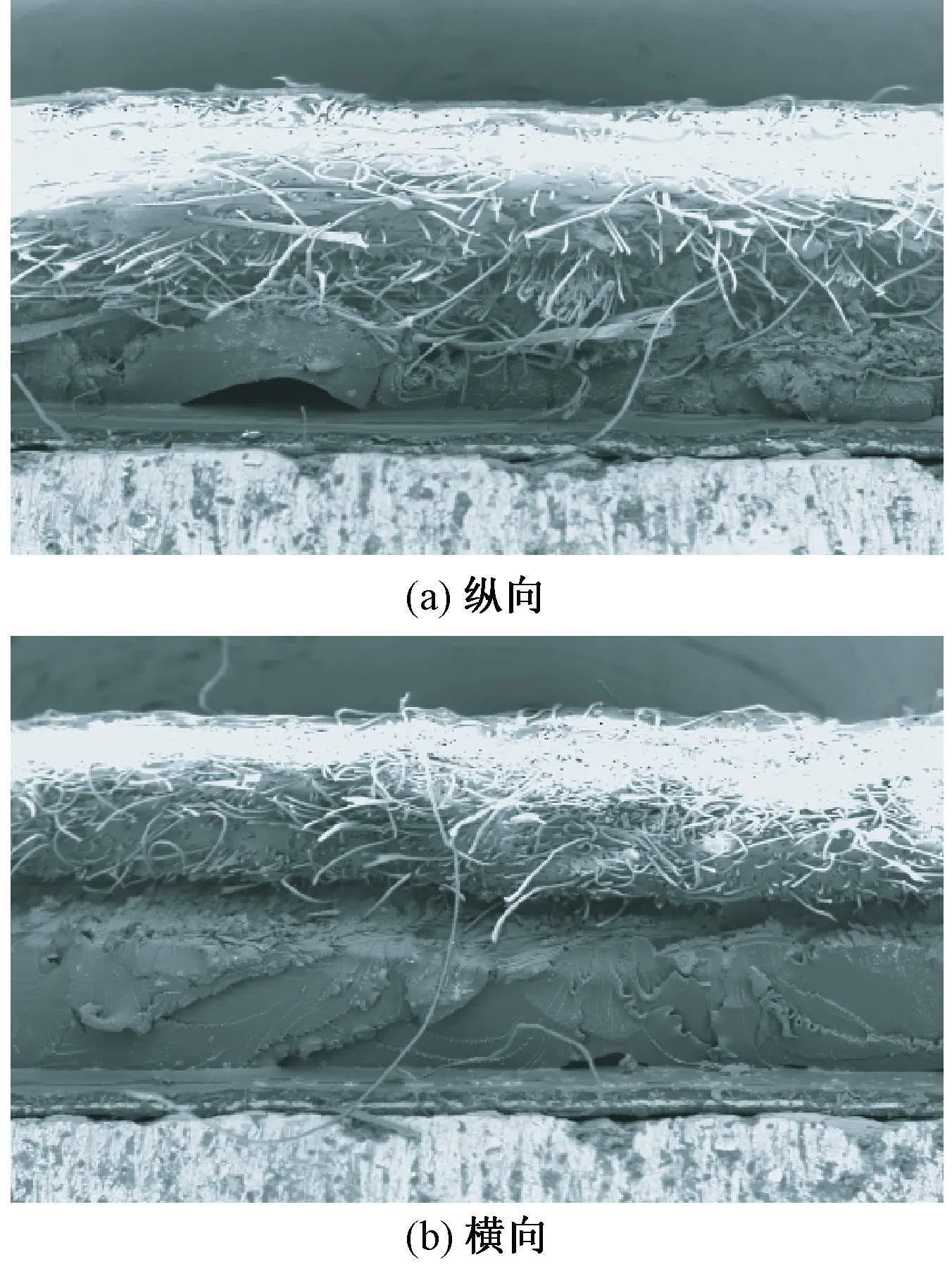
图4 涤纶/苎麻非织造复合材料的纵横向断裂面形貌(×50)Fig.4 Longitudinal(a) and transverse(b) fracture morphology of polyester/ramie nonwoven composites(×50)

在拉伸实验的过程中，涤纶/苎麻非织造复合材料表面的树脂层首先产生裂纹，然后裂纹随着拉伸强度的增加而逐渐增生扩散，并在很短的时间内复合材料发生断裂。在涤纶和苎麻混杂的纤维层断裂后，纤维从树脂基体中抽拔出，可以观察出断口表面凹凸不平，纤维断头较多，表明大多数的涤纶、苎麻纤维承受了载荷。这种以裂纹沿纤维束扩展而拉断的破坏模式与理论中假设的苎麻、涤纶层的拉伸断裂破坏模式一致，证明涤纶/苎麻非织造复合材料的理论临界体积分数和拉伸强度计算公式的可行性。

4 结 论

针对管道修复用涤纶/苎麻非织造复合材料在翻衬施工中易出现承压不足等问题，提出利用复合材料混合定律和胡克定律建立涤纶/苎麻非织造复合材料的理论临界体积分数和拉伸强度计算方法。

1)管道修复用涤纶/苎麻非织造复合材料的理论临界体积分数为17.7%，此时的理论拉伸强度最小。

2)管道修复用涤纶/苎麻非织造复合材料实验得到的临界体积分数为20%，理论与实际的临界体积分数区别不大，表明临界体积分数的计算公式具有一定实用性；然而由于苎麻、涤纶层的实际加工，及树脂浸润纤维不全面等误差原因，导致同组其他涤纶/苎麻非织造复合材料的拉伸强度实验值比理论拉伸强度低。

3)管道修复用涤纶/苎麻非织造复合材料实验得到的拉伸强度的变化规律与理论一致。即涤纶体积分数未到达临界体积分数时，拉伸强度随涤纶体积分数的增加而减小，到达临界体积分数之后，随涤纶纤维体积分数的增加而增大。

FZXB