盾构法T接隧道结构受力足尺试验研究
朱瑶宏, 高一民, 董子博, 柳 献, *
(1. 宁波大学建筑工程与环境学院, 浙江 宁波 315211; 2. 同济大学地下建筑与工程系, 上海 200092; 3. 宁波用躬科技有限公司, 浙江 宁波 315000)
0 引言
目前联络通道的施工方法包括明挖法、冷冻法以及机械法等,其中明挖法目前采用的较少,冷冻法是目前使用较多的工法[1-2],且有较为成熟的理论研究[3-4]。机械法联络通道在国外的应用较多: 德国汉堡第四易北河隧道安全通道,墨西哥Emisor Oriente隧道旁出支线。在国内的应用主要包括:香港屯门至赤鱲角连接路横通道[5],南京地铁盾构区间隧道联络通道施工。明挖法只能适用于地面较为开阔的环境;冻结法的工期一般较长,造价也较高[6]; 而采用机械法施作的联络通效率较高,但是相应的危险性也较高。本文主要以此进行研究。
国内外对此也从试验和数值等方面进行了研究。2007年,F.Y. Hsiao等[7]进行了岩土中隧道开洞的研究,提出了不同岩土等级对隧道开洞后主隧道响应的影响。2010年,P.Mayer等[8]研究了利用超前导管进行冻结法修建联络通道过程中的工法并利用有限元软件进行了相关的分析,这一工法中也采用了复合钢管片。2013年,A.Strauss等[9]进行了主隧道开挖联络通道的现场研究,在冻结法和支撑的帮助下,主隧道和内部设立的支撑应变量较小。2015年,P.Spyridis等[10]进行了开洞的二维和三维分析,通过开洞大小、约束条件等对这一问题进行了研究。2016年,LI等[11]计算了地铁车站隧道与施工隧道交叉口隧道衬砌变形及力学特性。2016年,A.Georg等[12]在岩体中利用TBM修建联络通道的过程中进行了相关检测,而且本工程隧道管片采用了复合管片。国内外对开洞的分析从岩石到软土,现场和数值都有较多的分析[13-16],但是有关室内试验的研究较少。
本试验依托宁波地铁联络通道施工新技术——盾构法施作联络通道的施工方法进行研究。通过研究隧道开洞过程,确定工况的变化以及测量结构的响应;通过模拟该施工过程中的出洞过程而设计的7环整环试验,可以得到各衬砌环结构在既定荷载条件下的结构裂缝、结构收敛变形、纵缝张开、环缝张开及错台、结构内力等指标。试验得到了切削主隧道衬砌结构这一过程中的响应,以期为后续工法开洞分析提供依据。
1 试验方案
1.1 加载系统
试验加载系统一共可以加载7环管片,每环包括24个加载点,每个加载点为可进行3种控制的液压千斤顶系统。加载装置如图1所示。
3种控制方法分别为荷载控制、位移控制以及荷载-位移曲线控制。荷载控制即加载至额定荷载,位移控制即控制千斤顶伸缩至固定位移值,荷载-位移曲线控制即根据土的基床系数和千斤顶位移确定此时的荷载值。

图1 加载装置
1.2 加载试件
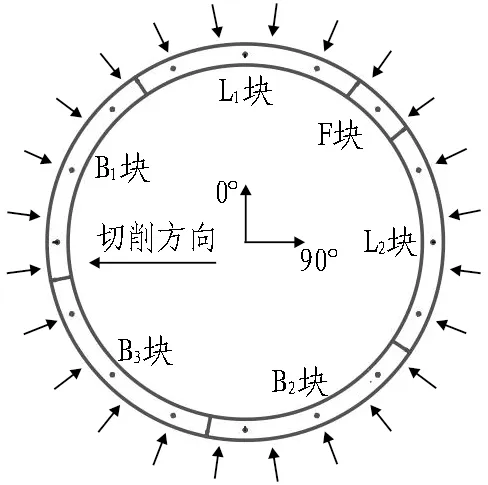
本试验的试件采用宁波地铁原型管片,衬砌环外径6 200 mm,内径5 500 mm,管片厚350 mm,4环标准环宽1 200 mm,3环特殊环宽1 500 mm。管片采用C50混凝土与HRB400钢筋,全环由1块封顶块(F,中心位置为45°)、2块邻接块(L1、L2)、3块标准块(B1、B2、B3)组成,封顶块弧度为20°,其余分块占据弧度为68°。特殊环的B1、B3块除开洞位置外其余部位采用钢管片。开洞位置为可切削混凝土,开洞位置为270°正中,开洞大小为盾构刀盘直径(3 290 mm,略大于联络通道直径3 150 mm)。纵向环间凹凸榫的刚度为70~100 kN/mm。管片的构造如图2所示。

图2 管片结构示意图
试验采用的7环管片,中间3环是盾构切削的管片,第4环为切削环,切削完成后洞口位置全部被切削掉;第3环和第5环为半切削环,切削结束后只有一半的管片被切削掉;其余4环为普通环。其中中间3环采用通缝拼装,其余4环采用错缝拼装。拼装方式和角度如图3和图4所示。试验中采用可主动施加预顶力的内支撑来保证隧道的整体稳定性,内支撑体系如图5所示。

(a) 试验正视图
(b) 试验左视图(选取第4环)
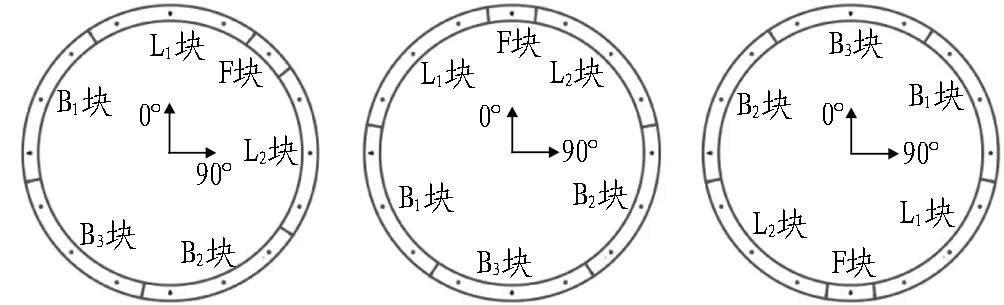
(a) 3/4/5环拼装示意图 (b) 2/7环拼装示意图 (c) 1/6环拼装示意图

图5 内支撑体系示意图
1.3 测试方案
为探究新型衬砌结构在设计状态下的结构响应,试验中测量和测试的内容包括结构收敛变形、纵缝张开及错台、环缝张开、主筋应变、混凝土应变、内支撑应变等。
1.4 荷载设计
试验根据3号线埋深14 m,侧压力系数取0.71,基床系数采用18 MPa/m。顶管机顶力维持在1 000~2 000 kN,最大顶力为2 000 kN。试验采用如下方式加载。
1)按照实际埋深设计,采用荷载控制的加载方式,各组千斤顶同步加载,分别按照设计荷载的0.20、0.40、0.60、0.70、0.80、0.85、0.90、0.95、1.00倍分9步加载至设计荷载;再将底部千斤顶修改为位移控制,将腰部千斤顶修改为荷载-位移曲线控制的加载方式模拟被动土压力。
2)内支撑结构分级加载至预定支撑力工况。按照10%分10级逐步加载,每根顶撑最终额定值为700 kN,每根前后撑最终额定值为50 kN。
3)模拟盾构正常切削,盾构开始切削管片,直至切削环破洞结束。
4)切削结束后将内支撑的撑力进行卸载,模拟切削完成后等待水土荷载稳定后进行内支撑卸载的过程。卸载过程采用预撑工况的加载表反向进行卸载。
2 试验过程
2.1 加载过程
试验过程选取第4环、第5环和第6环的顶底收敛变形进行描述,如图6所示。设计荷载加载至第9级后切削环、半切削环和普通环同步顶底收敛接近15 mm(图中特征点①);在保压后进行最后一级加载,各环顶底收敛增加至17 mm左右(图中特征点②);根据荷载位移曲线,在将腰部改为荷载位移控制后顶底收敛迅速减小至15 mm左右(图中特征点③)。施加顶撑的预顶力分为2级加载,2次均匀施加预顶力都使顶底收敛减少1 mm左右(图中特征点④和特征点⑤);在盾构切削管片后顶底收敛缓慢增加,切削盾构最大顶力达到1 700 kN(图中特征点⑥);在切削过程中将顶撑进行部分卸载,可以看到切削环的顶底收敛迅速增大1 mm(图中特征点⑦)。在切削完成后(见图7)进行内支撑顶撑的卸力,各环顶底收敛均匀增加2 mm左右,较初始工况,拆撑工况切削环的顶底收敛增大1 mm左右,其余增加不大(图中特征点⑧)。

图6 各环收敛变形曲线

图7 切削结束后内弧面示意图
2.2 加载过程中的结构性能
针对加载过程中各环的收敛变形,选择特殊工况对各环的结构性能进行研究。分别选取: 图6中特征点③,土体改为被动土压力的初始工况;图6中特征点⑤,内支撑施加顶撑撑力后的预撑工况;图6中特征点⑧,盾构始发结束后的工况;图6中特征点⑨,切削结束后内支撑卸力后的工况,为拆撑工况。
2.2.1 收敛变形
在整个切削过程中底部千斤顶采取位移控制,用来被动抵消其余各位置的千斤顶荷载,各环的底部收敛变化均较小,位移均在0.1 mm以内。所以顶底收敛与顶部向下的位移基本相同。
切削环在各工况下的收敛变形如图8所示。在设计荷载下,初始工况顶底收敛变形值为17 mm左右,腰部270°收敛变形值为-9 mm,腰部90°收敛变形值为-8 mm;预撑工况下,顶部收敛变形值减小至15 mm左右,腰部收敛变形值各减小至-8 mm和-7 mm;在盾构始发工况下,切削环腰部270°收敛变形值增加至-10 mm。盾构始发工况下,切削环在切削侧(325°)的接缝张开量增加2 mm。错台的现象与张开相似,切削侧(325°)的管片向内错台1~2 mm;拆撑工况下,切削环顶部收敛变形值增加至19.5 mm,腰部90°与270°收敛变形值增加至-11 mm和-9 mm。
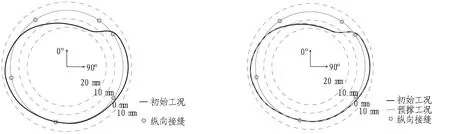
(a) 切削环初始工况收敛 (b) 切削环预撑工况收敛
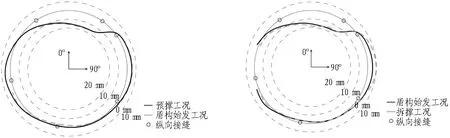
(c) 盾构始发工况收敛 (d) 拆撑工况收敛
半切削环收敛变形采用第3环为例,在各工况下的收敛变形如图9所示。在设计荷载下,初始工况顶底收敛变形值为16 mm左右,腰部270°收敛变形值为-8 mm,腰部90°收敛变形值为-8 mm; 预撑工况下,顶部收敛变形值减至14 mm,腰部收敛变形值均减少至-7 mm; 在盾构始发工况下,半切削环收敛变形几乎没有变化; 拆撑工况下,半切削环顶部收敛变形值增加至18 mm,腰部90°与270°收敛变形值增加至-10 mm;半切削环的接缝张开几乎没有变化。
普通环收敛变形采用第2环为例,在各工况下的收敛变形如图10所示。在设计荷载下,初始工况顶底收敛变形值为16 mm,腰部270°收敛变形值为-8 mm,腰部90°收敛变形值为-7 mm;预撑工况下,顶部收敛变形值减小至14 mm,腰部收敛变形值分别减小至-7 mm和-6 mm;在盾构始发工况下,普通环收敛变形几乎没有变化;拆撑工况下,普通环顶部收敛变形值增加至17 mm,腰部90°与270°收敛变形值分别增加至-9 mm和-8 mm;普通环的接缝张开量几乎没有变化。

(a) 半切削环初始工况收敛 (b) 半切削环预撑工况收敛
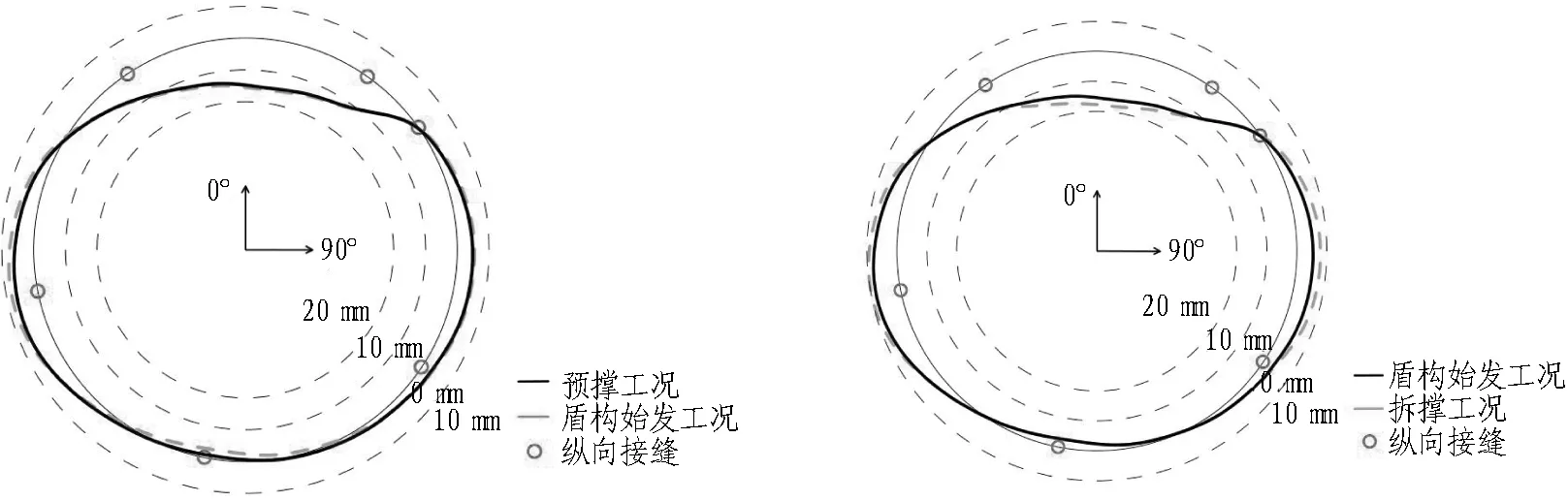
(c) 半切削环盾构始发工况收敛 (d) 半切削环拆撑工况收敛

(a) 普通环初始工况收敛 (b) 普通环预撑工况收敛
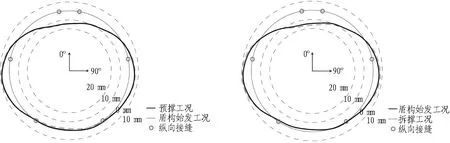
(c) 普通环盾构始发工况收敛 (d) 普通环拆撑工况收敛
除了各环的收敛变形,还测量了环间的环缝张开。各环环间环缝的张开量均在2 mm以内,中间3环顶底腰部的张开在最后3个工况中变化均不大,整体性较好。
2.2.2 结构内力
结构内力拟采用2个工况之间对比的方式进行绘制描述。切削环内力如图11所示。
切削环初始工况顶部正弯矩和腰部负弯矩大约为180 kN·m,顶底位置轴力最小,腰部轴力最大。顶底初始轴力在1 400 kN左右,腰部初始轴力在1 600 kN左右。在预撑工况下,可以看到由于腰部的外荷载增大,顶部弯矩减小至180 kN·m,腰部弯矩下降20 kN·m左右;预撑工况下腰部轴力减少400 kN,顶部轴力几乎不变。盾构始发工况下顶部弯矩靠近切削侧(270°)开始减小,减小30 kN·m左右,靠近靠背侧(90°)的弯矩增大10 kN·m左右;顶部轴力减小300 kN左右,从横鸭蛋形向喇叭形过渡,轴力整体变化不大。在内支撑进行卸力后,顶部弯矩增大30 kN·m左右,腰部弯矩增大10 kN·m左右;顶底和腰部轴力均增大200 kN左右。

(a) 切削环初始弯矩图(单位: kN·m) (b) 切削环初始轴力图(单位: kN)

(c) 切削环预撑工况弯矩图(单位: kN·m) (d) 切削环预撑工况轴力图(单位: kN)
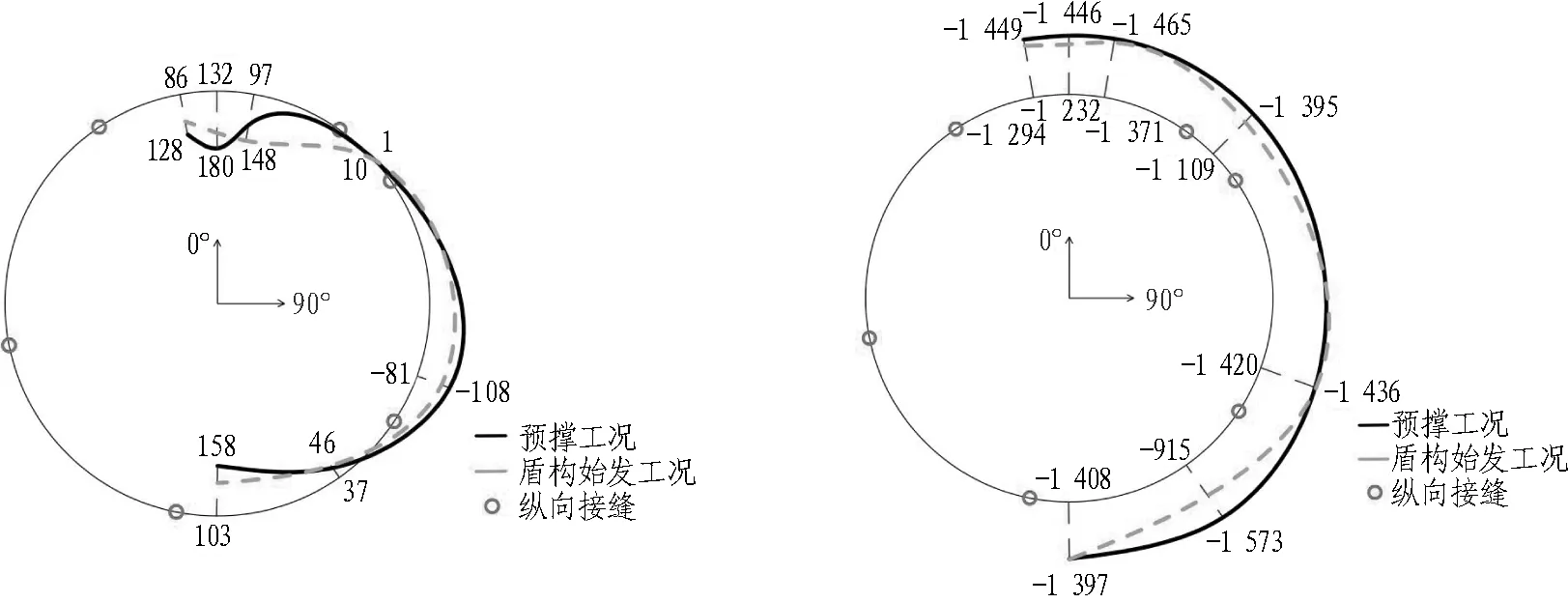
(e) 切削环盾构始发工况弯矩图(单位: kN·m) (f) 切削环盾构始发工况轴力图 (单位: kN)

(g) 切削环拆撑工况弯矩图(单位: kN·m) (h) 切削环拆撑工况轴力图(单位: kN)
半切削环的内力分布如图12所示,由于对称性这里选取了半切削环第3环的内力进行分析。
半切削环初始工况顶部正弯矩和腰部负弯矩为180 kN·m左右,顶底位置轴力最小,腰部轴力最大。顶底初始轴力在1 400 kN左右,腰部初始轴力在1 600 kN左右。在预撑工况下,由于腰部的外荷载增大,顶部弯矩减小至160 kN·m,腰部弯矩下降20 kN·m左右。预撑工况下腰部轴力减少400 kN,顶部轴力几乎不变,与切削环几乎相同。盾构始发工况下顶部弯矩靠近切削侧(270°)的开始减小,减小10 kN·m左右,较切削环的减少量小;在切削结束后,半切削环的弯矩变化不大,轴力整体变化也不大。在内支撑进行卸力后,顶部弯矩增大30 kN·m左右,腰部弯矩增大50 kN·m左右,顶底和腰部轴力均增大200 kN左右。
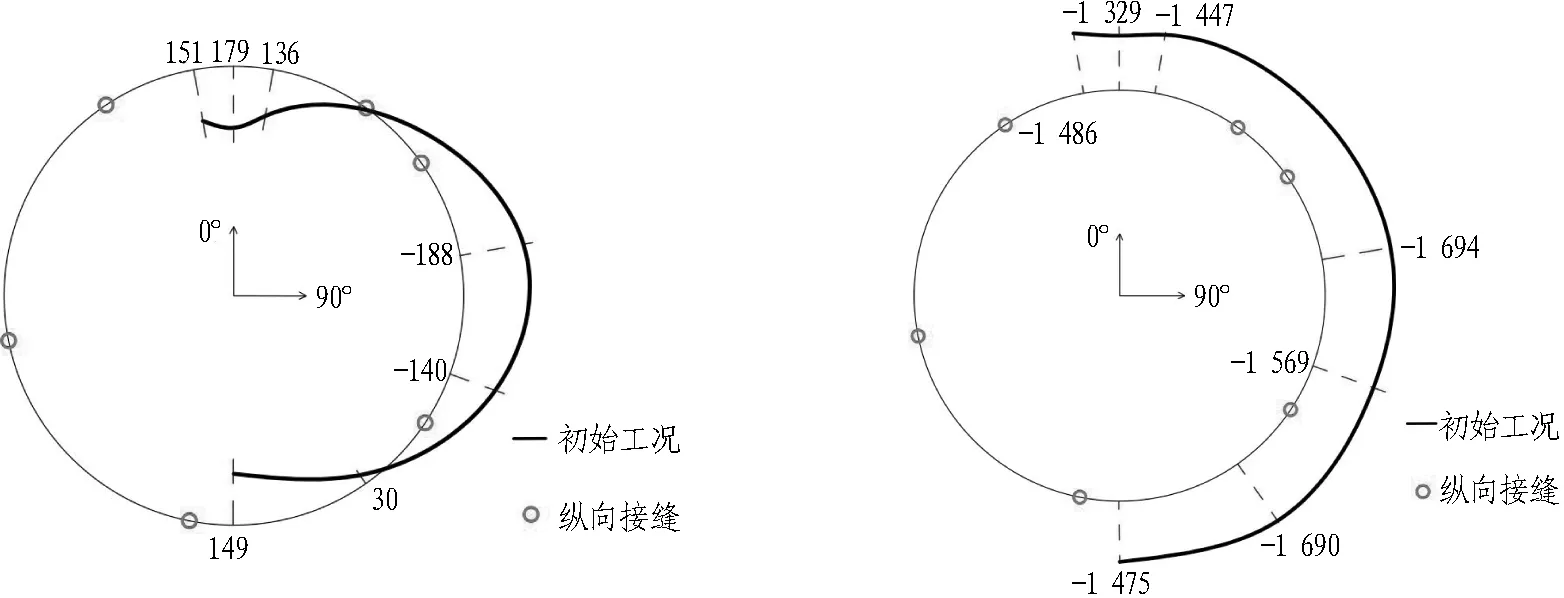
(a) 半切削环初始工况弯矩图(单位: kN·m) (b) 半切削环初始工况轴力图(单位: kN)

(c) 半切削环预撑工况弯矩图(单位: kN·m) (d) 半切削环预撑工况轴力图(单位: kN)

(e) 半切削环盾构始发工况弯矩图(单位: kN·m) (f) 半切削环盾构始发工况轴力图(单位: kN)

(g) 半切削环拆撑工况弯矩图(单位: kN·m) (h) 半切削环拆撑工况轴力图(单位: kN)
由于对称性,选取了普通环第2环的内力进行分析,普通环的内力分布如图13所示。初始工况下,普通环顶部正弯矩和腰部负弯矩约为140 kN·m,顶底位置轴力最小,腰部轴力最大;顶底初始轴力在1 100 kN左右,腰部初始轴力在1 200 kN左右。在预撑工况下,由于腰部的外荷载增大,顶部弯矩减小至135 kN·m,腰部弯矩下降10 kN·m左右;腰部轴力减少100 kN,顶部轴力几乎不变,与切削环几乎相同。盾构始发工况下顶部弯矩增加5 kN·m,腰部(90°)弯矩增大20 kN·m左右,轴力整体变化较小。在内支撑进行卸力后,顶部弯矩增大5 kN·m左右,腰部弯矩增大20 kN·m左右;顶底和腰部轴力均增大200 kN左右。
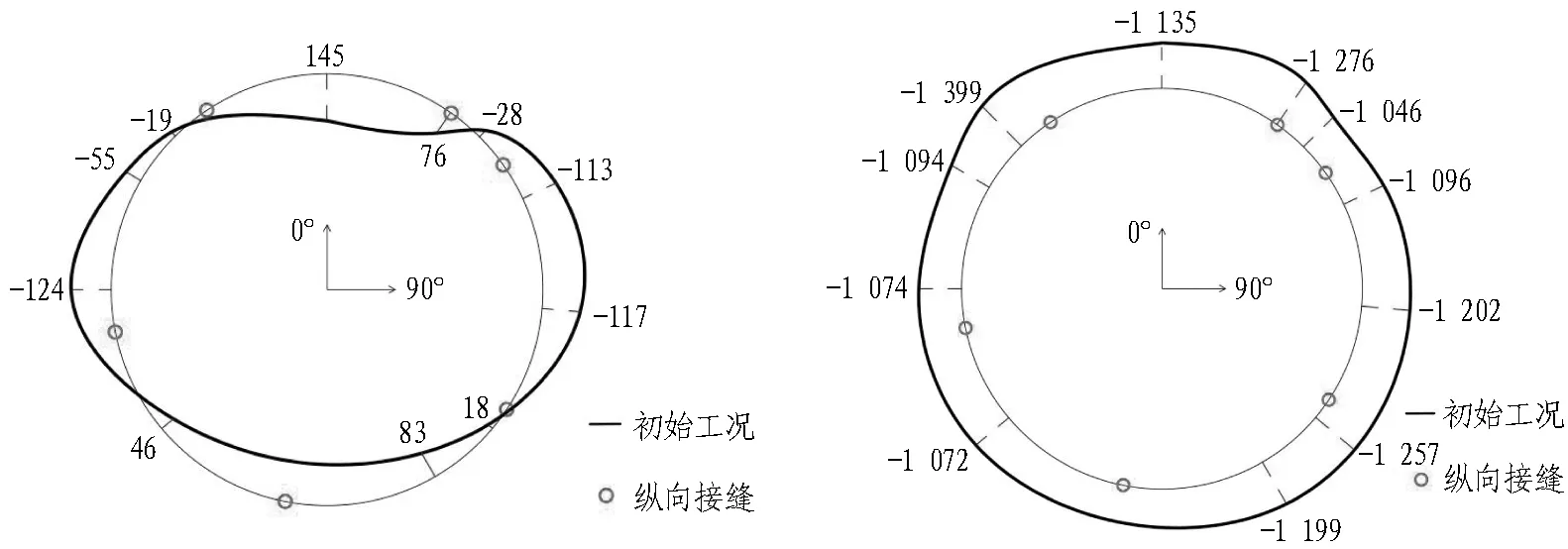
(a) 普通环初始工况弯矩图(单位: kN·m) (b) 普通环初始工况轴力图(单位: kN)
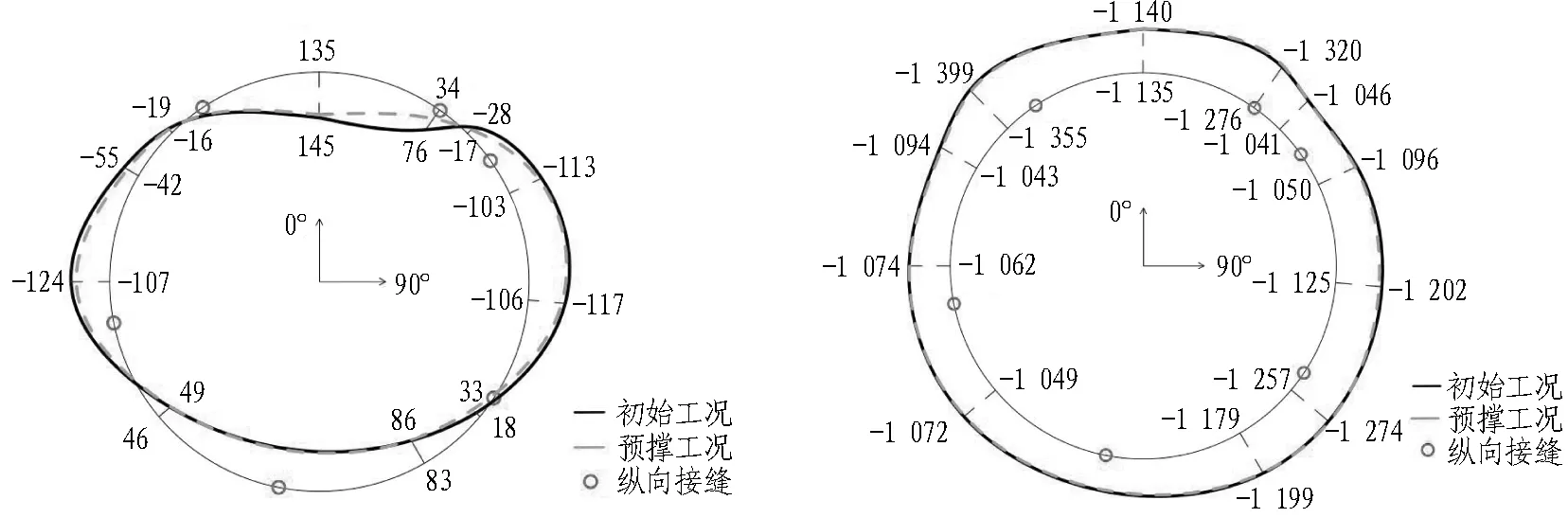
(c) 普通环预撑工况弯矩图(单位: kN·m) (d) 普通环预撑工况轴力图(单位: kN)

(e) 普通环盾构始发工况弯矩图(单位: kN·m) (f) 普通环盾构始发工况轴力图(单位: kN)

(g) 普通环拆撑工况弯矩图(单位: kN·m) (h) 普通环拆撑工况轴力图(单位: kN)
2.3 内支撑结构响应
试验还测试了内支撑系统后撑的受力情况: 后撑内侧中心线的纵向应变在始发工况前基本在50 με以下,在盾构始发的情况下应变达到100 με左右;在拆撑工况后,应变又恢复到50 με以下,整体应力值较小;在环向方向上,整个后撑的应变变化不明显,环向上的弯曲不明显。由实测数据可得,内支撑环向和纵向的弯曲都不明显。
3 破洞效应探究
通过收敛变形和内力的变化规律,从初始工况、预撑工况、盾构始发工况与拆撑工况4个工况总结破洞效应。
1)在没有切削的初始工况下,各环之间的收敛以及内力是基本相似的,模拟了在实际地层中隧道的受力情况。
2)在预撑工况下,可以看到整体各环的收敛变形与内力变化一致,包括没有收到预撑直接影响的第7环收敛也有相类似的收敛变形。环间作用较好,基本可以协调变形。
3)在盾构始发工况下,切削环的切削侧(270°)发生2 mm向外的收敛变形,其余位置由于内支撑结构的作用变化不大。靠近切削侧(270°)的内力发生较大的变化,其弯矩增大,靠近靠背侧(90°)弯矩减少,半切削环相应位置的弯矩也有部分变化。最终切削完成后,半切削环的内力变化类似于切削环的内力变化,幅度较小,普通环几乎没有内力变化。这一过程中,结构体系发生变化,主要是切削环靠近切削侧(270°)内力变化较大,其余变化较少。
4)在拆撑工况下,切削环的顶部弯矩迅速增大,腰部弯矩也增大。半切削环受此影响也产生了相同的效应,变化方向相同,直至稳定。普通环的变化趋势相同,数值较小。
5)隧道破洞拆撑后整体收敛变形较为稳定,变化在5 mm以内,主隧道结构内力变化维持在80 kN·m以内。
综上所述: 环间作用较强的隧道局部破洞的过程中,越靠近切削侧(270°)的内力变化越明显,远离切削侧的各环变形与内力(0°~180°)基本协调;各个工况下只有切削环的切削侧(270°)在盾构始发工况下有较大的内力变化,其余位置的其余工况基本为协调变化,包括拆撑工况下的切削环。
4 结论与建议
通过对宁波地铁3号线盾构法联络通道1∶1模型试验的研究,研究7环管片在中间环破洞后的整体隧道响应,可得到以下结论。
1)隧道局部破洞以后整体隧道的裂缝较小,整体性完好,各环监测部位内力也较小,该工法是安全的。
2)在整个试验过程中,在没有考虑联络通道结构对结构支撑作用的前提下环间作用较好,7环的变形与内力虽然有差异,但基本是相互协调的。主要发生的不平衡荷载在于盾构始发阶段切削过程中切削环切削部位单独受力,切削部位对称位置是较为均匀的受力状态。建议在实际工程中严格控制盾构的顶进力,使切削侧的内力变化在可控范围内。
3)所有试验环变形和内力变化最大的工况是拆撑工况,由于整体性,切削环顶底收敛只比其余环大0.5~1 mm。内力顶部弯矩的增加和腰部弯矩的增加与半切削环基本相似,相差较小;环间传力基本集中在中间3环,其余4环的影响较小;普通环几乎没有内力的变化。建议在实际工程中重点关注监测切削位置中间3环的变形与内力,其余各环的变化较小,可进行一般性监测。
4)在切削过程中,由于内支撑刚度较大,各环的收敛变形与内力变化均较小,环间传力现象不明显。相比较而言,拆撑工况是所有工况中环间传递最为明显的工况,建议可以通过修改内支撑结构体系,使全过程环间传力较为均匀。
通过本文进行的盾构法联络通道施工方法的足尺模拟试验,探寻了多环管片开洞后的安全性问题,明确了内力重分布发生的主要位置和传力过程发生的主要工况。一方面验证了足尺试验模拟施工过程的可行性,今后新工法的推广可以采用类似的模拟方法;另一方面本试验为类似条件下推广该工法提供了理论支持。但是在本文的研究中,没有考虑联络通道本身结构对主隧道结构的影响,本质上联络通道本身结构的存在是有利于结构受力的,更有利于环间传力,在后续研究中,应该考虑这一影响;同时,对于盾构法联络通道进洞过程还需进一步研究。

