思维导图在突破中考代数几何综合题中的探索和运用

罗宇珊

【摘要】  中考代数几何综合题，历来是拉开分值关键题目，难度非常大。传统的思路和方案，教学成果并不突出。本文运用思维导图的教学方式，探索采用形象化、网络化、结构化的思维模式，在代数几何综合题中帮助学生找出界点，分类讨论方面取得一定的成效，从而实现高分突破。

【关键词】  思维导图 初三数学复习 代数几何综合 界点

【中图分类号】  G633.6               【文献标识码】  A     【文章编号】  1992-7711（2020）04-134-02

思维导图，是一种利用图像进行思考的辅助工具，可以比较形象化地帮助学生快速梳理和把握知识点之间联系，有利于学生构建完整的知识网络体系，帮助其记忆与理解，培养学生创新思维，快速提高学生的学习质效。

中考代数几何综合题，是中考试卷中的最后一道大题。其分值达到9分，往往成为学生拉开分值的关键题目。对于学生冲刺中考数学高分，甚至是满分，起着非常关键的作用。笔者在多年的教学实践中，巧妙探索引入思维导图方法，帮助学生构建形象化、网络化的知识架构，提高了学生解决几何综合体的能力和水平，收到了不错的教学效果。以2019年6月的中考成绩为例，笔者所任教的两个班级学生数学成绩优秀率为94.35%，高分人数21人（共89人参加考试）从而印证了日常教学中思维导图的训练对学生实现高分突破方面，取得了较好的成效。现分三个方面阐述如下。

一、代数几何综合题的题型特点及思维导图方法的解题优势

代数几何综合题是中数数学中覆盖面最广、综合性最强的题型，对于提高学生分析能力和综合素养发挥着重要作用。一般来讲，其题型设计主要是把代数中的数学公式、函数，几何中的三角形、四边形等图形变换，以及几何数学解题方法等内容，有机地结合在一起，进行开放性、关联性问题研讨，从而培养学生发散性思维。不难看出，常规的学习方法及解题思路，难以有效将复杂、广泛的知识内容，有机融合、熟练应用，以至于此类题目往往成为日常教学及解题的重点和难点，师生投入精力大但收效不尽如人意。

思维导图方法，其特点是迅速为学生构建完整知识网络体系，让学生在脑海中，对整个数学知识体系和建构有个形象认识和宏观把握。可以让学生更加直观地记忆各个知识点的内容及相关之间的逻辑关系，很好地克服代数几何综合体解题中的难点和困难。从实际教学效果来看，也有效印证了这一点。师生教学互动中，不少学生反映，考场上时间紧张，面对代数几何综合题，往往难以快速把握解题要领，可谓事倍功半。采用思维导图教学方法后，感觉脑海里逐渐形成了一张比较清晰全面的知识关联架构图，考试过程中熟练灵活应用，很快助力自己找到解题的方向和重点，如有神助。

二、日常教学中，培养学生思维导图解题思路的方案和步骤

常言说，“工欲善其事必先利其器”。要想在解题中熟练应用好思维导图思路，首先要辅导学生构建数学关键知识点网络，让学生对整个数学知识点有个全面的认知和把握。

笔者在实际教学中，先辅导学生从代数与几何两大方面，通过回忆关键知识点，自主构建绘制思维导图，让知识要点、逻辑关系在学生脑海中变动鲜活、生动、直观。具体来讲，代数方面主要是分一次函数、二次函数、反比例函数、三角函数等维度构建思维导图;几何方面，是通过三角形、四边形等图形相关的线段位置关系的判断、数量关系或者面积的计算等维度构建思维导图。

日常教学中，将绘制、完善过程与中考复习过程有机统一，帮助学生不断加深对知识点和逻辑关系的理解把握，增强记忆效果，从而达到高效复习和提高解题能力的目的。

三、分三种题型，阐述思维导图在解题中的具体应用

代数几何综合的类型大致可以分为动点型、动线类及动图类等三种类型的探究题。现介绍分析解题过程如下。

（一）动点型探究题解题应用，思路更清晰。

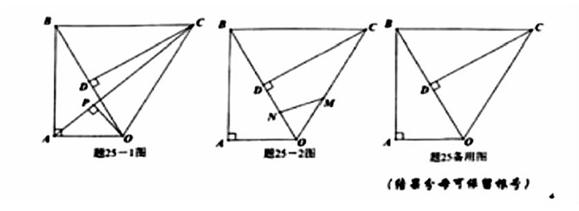
例题：广东省2018年中考数学卷第25题

本题大致题意：Rt△OAB，顺时针旋转60°得到下图。第一问直接求出∠OBC度数，第二问通过连接AC，作OP⊥AC，求OP的长度。第三问则是一个双动点，求函数解析式及最值的问题。

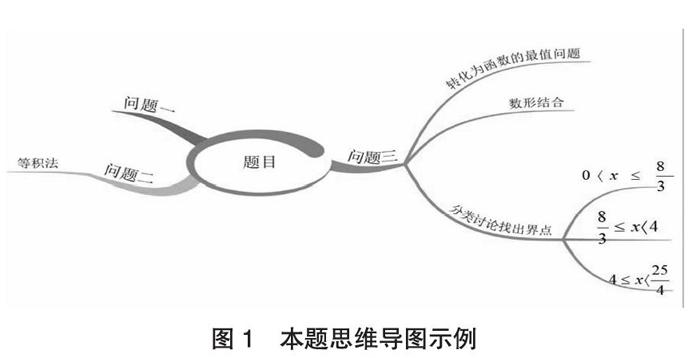
此题中，先找到此题涉及的知识点：“旋转图形的性质、求三角形第三边上的高、函数的最值问题”，第一和第二问题都比较简单，难点在第三问题。如何突破难点，关键在于找到运动过程的界点，当0≤x≤8/3时N、M分别在OB和OC上，此时由M向OB边上作垂线段即是三角形的高，可用三角函数表示出高的长度，以及表示出底，便可以表示出面積。当8/3≤x<4时，即M点运动到BC上而N点还在OB上的时候，同样的方法表示出高的长度。当4≤x25/4<时，即M、N两点均运动到BC上时，此时三角形的高为AB，而表示出底即可以表示出面积。

运动过程确定后，就可以利用思维导图的形式展开思路。这样的思路让解题过程更清晰，书写时也不容易出现思路中断或思维混乱的情况。根据思维导图的思路很容易写出规范的解题步骤。

图1 本题思维导图示例

（二）动线型探究题解题应用，分析更全面

例题：广东省2016年中考数学卷第25题

本题大致题意：正方形ABCD的一边BC在其所在的直线上平移得到的新线段，通过连接相应的点，作垂直等得到如下的图形。该题同样设置三个问题：（1）直接判断四边形APQD是什么四边形？

（2）判断两条线段的数量关系和位置关系，并加以证明。（3）在平移变换过程中，求函数的解析式及最值问题。

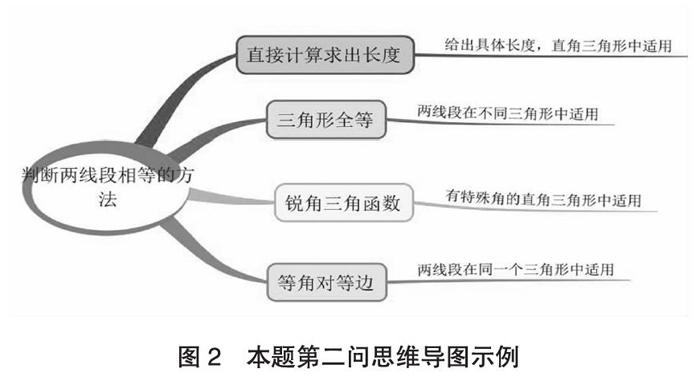
此题中，第一问大多数学生可以轻松回答。第二问中判断两条线段的数量和位置关系，考生通过看图，便可以猜出相等于与垂直。但是如何去证明呢？我们可以通过简单的思维导图加以分析找到方法。通过简单分析，便可找到本题可通过△ABO与△PQO全等证明OA、OP两条线段相等，从而由全等三角形对应角相等，轻松证明∠AOP为直角。

图2 本题第二问思维导图示例

第三问，是本题的失分点，也是本题难点。而本题给出的两个图形其实已经提醒学生，本问中线段PQ运动方向可以向左与向右，那么，分类讨论成为解决本问的关键，下面，借助思维导图，对第三问进行分析。

图3 本题第三问思维导图示例

（三）动图型探究题解题应用，难点易突破

例题：2013年广东省中考数学卷第25题

本题大致题意：一副直角三角板现固定其中一块三角板ABC，将三角板DEF沿射线BA方向平行移动有关数学问题。如图所示，设置了以下三个问题：（1）如图②，求∠EMC的度数;（2）如图③，当EF经过点C时，求FC的长;（3）求函数的解析式已经自变量取值范围的问题。

此题中，阅读量较大，学生得分率较低，出现问题的主要原因是：题目新颖，畏难心理？学生花费时间多，找不到突破口。但是事实上，中考最后一道代数几何综合的题目，都是会分为三小问，其中第一问通常情况下都是比较简单，绝大部分的学生是可以解决的。

本题第一问，可以直接利用三角形的外角和定理快速解决，只是，如何在考场上紧张紧迫的时间内，迅速想到本题所考察的知识点，还是要依仗平日里的积累和思维训练。为此，我们在平日里的教学以及中考的复习中，需要坚持引导学生画思维导图，目的就是在考场上能对问题作出快速而正确地反应。

本题第二问中，求CF的长度，我们可以在脑海里呈现出求直角三角形中线段方法的思维导图：一、勾股定理，二、三角函数，三、等积法……这样便可迅速通过阅读题目，找到本题的解题方法：利用三角函数求解。

本题第三问，即为本题的拉分题，考生可以通过分析整个运动过程，画出思维导图。利用这种方法既容易找到突破口解决问题，又可以缩短解题的时间。

图4 本题第三问思维导图示例

综上所述，采取思维导图解题，可收事半功倍之效。学生在升中考试前复习中，可以翻看温习自己构建的思维导图，不断强化理解和巩固记忆。力争做到，让思维导图中的知识架构和逻辑关系，入脑入心，转化為自身潜意识的一部分。如此，在进入考场后，熟练掌握和灵活应用脑海中的思维导图，可以帮助学生迅速理清思路，抓住要领、实现快速解题，从而取得优异的成绩。思维导图方式，只要学生平时能够多加练习、多加运用，熟能生巧，掌握规律，考场上就会感觉如有神助，取得意想不到的收获。

[ 参  考  文  献 ]

[1]李晓鹏.中学生思维导图学习法光明日报出版社.

[2]广东省初中毕业生学业考试试卷（2013年、2016年、2018年）.

[3]《万唯中考试题研究》.