整体建构中考复习，强化结构思维水平

张勇

【摘要】  单元复习课的设计应该注重整体教学，设置适宜的问题或活动，加深学生对所学内容系统性的认识，明晰知识间的联系以及研究思路与方法，提升学生的思维水平。

【关键词】  整体 系统 单元复习 平行四边形

【中图分类号】  G633.6                       【文献标识码】  A 【文章编号】  1992-7711（2020）05-108-03

缘起

教材的整体设计呈现不同知识之间的关联。一些知识之间存在着实质性的联系，这种联系体现在相同的内容领域，也体现在不同的内容领域。帮助学生理解实质性联系，是数学教学的重要任务。在九年级复习期间，如何借助结构性的问题帮助学生从整体的视角更好地建构知识体系，深刻理解知识间的内在联系就显得尤为重要。

基于上述思考，笔者对单元整体复习展开了研究。一方面通过结构性的问题和数学活动帮助学生把单元知识的巩固和应用形成整体的认知结构，另一方面把教材中的点状知识关联成网状知识结构，把相关联的其它单元知识进行重构和拓展。让学生在复习课中收获解决一类问题的一般性思维策略和方式、方法。笔者以平行四边形单元复习为例，从整体的视角阐述在复习课中如何有效提高学生的认知水平，从而实现提升学生的数学素养和思维能力的目标。

教学设计

一、内容和内容解析

1.内容

平行四边形及矩形、菱形、正方形的定义、性质及判定.以及运用这些内容解决问题。

2.内容解析

该单元是在学生复习了三角形的相关知识（其中包括特殊三角形直角三角形、等腰三角形）、全等三角形和轴对称知识的基础上，进一步复习四边形的知识。

三角形的学习基本路径为定义、性质、判定、应用，从一般到特殊。这些学习经验为后续平行四边形等内容的复习奠定了基础，提供了“一般观念”的示范作用.

平行四边形是边的大小关系、位置关系、角的大小关系，对角线的关系特殊化而得到的特殊四边形。而矩形、菱形、正方形亦是边角对角线特殊化的平行四边形类比三角形的复习建构路径，通过一系列思维活动过程，再一次呈现“一类几何图形特例研究的一般套路”。

基于以上分析，本单元的教学重点是：平行四边形、矩形、菱形、正方形的定义、性质及判定，以及这些内容之间的联系。系统化建构知识体系。

二、目标和目标解析

1.通过探究活动回顾平行四边形及矩形、菱形、正方形的定义、判断、性质，以及它们之间的关系。

2.能运用性质和判定进行推理论证和定量计算。

3.能运用相似三角形、勾股定理、面积法等方法，解决特殊四边形相关的定量问题;通過解决特殊四边形的定量问题，感受相似三角形、勾股定理、面积法是通法。

4.能通过探究活动，体会平行四边形及矩形、菱形、正方形的研究思路、研究内容、研究方法。

5.经历构建知识体系的过程，总结归纳一类几何图形特例研究的一般套路。

基于以上分析，本单元的教学难点是：联系三角形的知识结构体系，建构四边形知识结构体系，并能把四边形问题化归为三角形问题来解决，促进学生系统地思考问题。

三、教学过程

1.学情前测

（1）已知平行四边形相邻两条边的长度之比为3：2，周长为20cm.则它各条边长为 _________ .

（2）矩形具有而平行四边形不一定具有的性质是（    ）

A.对角相等 B.对边相等C.对角线相等 D.对角线互相平分

（3）已知菱形的周长为4，两条对角线的和为6，则菱形的面积为 _________ .

（设计意图：根据最近发展区理论，教学应该尽可能地从学生的认知水平出发，重视学生已有的经验展开课堂活动。在本节专题复习课之前，学生已经学习过平行四边形及矩形、菱形、正方形的定义、性质、判定，这些都是本节复习课的重点知识。笔者所教学的是杭州某公办学校九年级班级，实际掌握情况中仅第2题出现3人答案错误，1人空白。因此，通过前测的设计，从数学内部旧知的角度评估学生的掌握情况。）

2.激活旧知

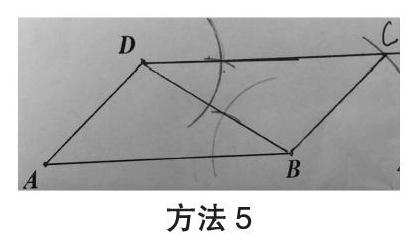
活动1：利用直尺和圆规画出以AB，AD为边的平行四边形。（要求保留作图痕迹）

追问：你的作图依据是什么？

师生活动：学生呈现不同画法，并通过推理论证自己的画法。

方法1                                         方法2

方法3                                     方法4

（设计意图：设计开放的数学活动，给学生提供了体验式的活动经验，调动学生参与积极性。同伴分享的过程又给了学生借鉴学习的机会。以此作为问题驱动，通过思考、证明、讨论、分享这些活动，积累思维活动的经验，发展学生的学习内驱力，从而达到旧知的复习以及新知的联系。学生的不同生成激活了学生对平行四边形定义、性质、判定做的认识。引导学生按研究路径进行知识梳理）

3.联系建构

问题：我们复习了三角形相关知识，是按照怎样的路径研究的？

师生活动：学生回忆三角形的研究路径——定义、性质、全等关系。特殊三角形的研究路径——定义、性质、判定等。

追问1：回忆三角形性质、判定的研究视角，类比三角形的研究视角从不同视角（边、角、对角线）回忆平行四边形的定义、性质、判定。

师生活动：学生梳理平行四边形的定义、性质和判定。

追问2：矩形、菱形、正方形分别是把平行四边形的什么元素特殊化而来的？

（设计意图：对几何图形的研究按照从一般到特殊的思路进行，比如直角三角形，它是一般三角形从角特殊化得到的.等腰三角形，它是从边特殊化得到的。通过类比三角形构建研究思路，用相似的思路研究不同的问题.引导学生自主构建知识体系、深化理解。）

4.化归本原

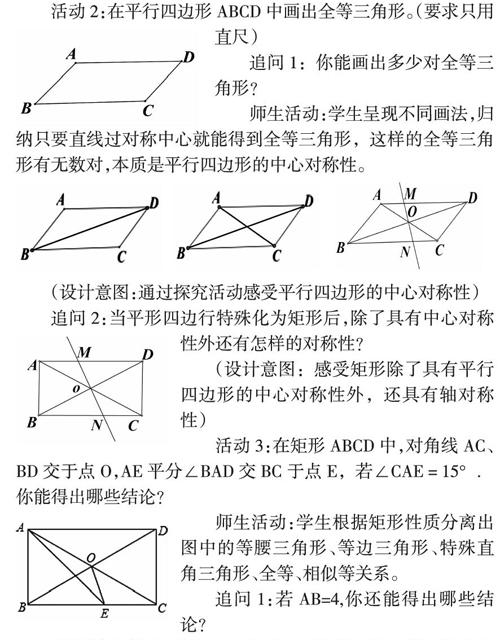
活动2：在平行四边形ABCD中画出全等三角形。（要求只用直尺）

追问1：你能画出多少对全等三角形？

师生活动：学生呈现不同画法，归纳只要直线过对称中心就能得到全等三角形，这样的全等三角形有无数对，本质是平行四边形的中心对称性。

（设计意图：通过探究活动感受平行四边形的中心对称性）

追问2：当平形四边行特殊化为矩形后，除了具有中心对称性外还有怎样的对称性？

（设计意图：感受矩形除了具有平行四边形的中心对称性外，还具有轴对称性）

活动3：在矩形ABCD中，对角线AC、BD交于点O，AE平分∠BAD交BC于点E，若∠CAE=15°.你能得出哪些结论？

师生活动：学生根据矩形性质分离出图中的等腰三角形、等边三角形、特殊直角三角形、全等、相似等关系。

追问1：若AB=4，你还能得出哪些结论？

师生活动：学生回答，互相补充。归纳得出图中所有线段均可求，所有的角均可求，所有图形的周长面积均可求，线段比、面积比也可通过不同方法求解。

追问2：在求解的过程中你用了什么方法？

师生活动：小组内交流归纳如下

类型1：求线段类的方法：相似（全等）三角形、勾股定理、三角函数、面积法

类型2：求角度类的方法：相似（全等）三角形、三角函数。

类型3：求面积类的方法：相似（全等）三角形、割补法

追问3：试着自己提出问题，并解答。

师生活动：改变题目的条件，例AB=4改为AB=3，BC=4等。

（设计意图：从定性到定量，既利用性质推理论证又通过解决矩形的定量问题，感受四边形问题通常是化归为三角形问题来解决，而相似三角形、勾股定理、面积法等方法是解决问题的通法。）

活动4：如图，正方形ABCD，AD=4，请按如下要求作图：取BC的中点E，连结AC与DE相交于点N，F为AB上一点，连结DF交AC于点M，当△AFM和△CEN相似时，求AF的長。

师生活动：分类讨论，归纳每一种情况所用方法，进一步感受正方形性质的丰富。

（设计意图：正方形是特殊平行四边形中具有代表性的一类，正方形既是轴对称图形，又是旋转对称图形。通过探究活动感受正方形的对称性，并利用对称性解决问题.）

反思

1.整体立意，系统建构

三角形的研究，经历了一般到特殊的图形研究的过程。研究三角形的视角：边、角、三线，这也是研究三角形的基本思路和方法。有了这样的研究经验和基础，站在系统的高度，设置恰当问题引导学生类比三角形的研究，正迁移研究方法和思路展开对四边形的研究。感知平行四边形是四边形特殊化而来，进一步特殊化得到矩形、菱形，再进一步特殊化得到正方形这样的过程。

体验从边、角、对角线的视角来研究特殊四边形的基本思路和方法，凸显系统化，整体性。学生学会的不是单一的知识，也不是解决某一个问题的具体方法，而是解决一类问题的一般性思维策略和研究几何图形问题的方式和方法.因此，这是从“具体方法”到“思维策略”的提升。

2.加强直观，思维可视

通过画图操作、探究等活动，用数学实验的方式加强对图形的感觉、认识、分析、推理。引发学生的思考，调动已有知识和活动经验，来寻求解决问题的思路。动手动脑的过程，让学生经历从实验到论证的过程，经历从合情推理到演绎推理的过程。利于学生的思维从直观到抽象，从感性到理性的飞跃，发展学生问题解决的能力。

画图呈现的过程也是思维可视化的过程。说明作图依据的过程是演绎推理的过程。只有学生参与了主动实践、观察、思考的过程，才能有所发现，提出问题，才能有效地落实四基四能。

3.过程开放，拓展提升

每位学生独立完成画图的过程。呈现不同的画法和说明依据的过程，让学生表达思考的过程，经历了从操作到思辨到逻辑推理的过程，发展了逻辑思维能力和数学语言表达能力。拓展了思维空间，激发了学生从不同角度思考问题，发展思维的灵活性。

不同方法的呈现既促进学生同伴间的互相借鉴，又引发学生主动整理知识，自发完善结构体系。开放的问题设计，有利于面向全体，让每个层次的学生都有参与的可能，都有参与的空间，思考的空间，提升的空间。

4.转化化归，回归本质

巧妙利用问题串在知识的横向联系和知识体系的纵向联系中引导学生去体验感受。尤其是知识的纵向联系上，笔者通过活动3，活动4让学生充分感受特殊平行四边形的定量探究问题是通过转化为三角形，迁移应用三角形知识来解决问题。模型思想、分类讨论、转化化归思想、方程思想等数学思想方法的归纳总结，帮助学生有效提升数学学科素养。

[ 参  考  文  献 ]

[1]义务教育数学课程标准（2011版）.

[2]陈锋，薛莺认知引领关联探究重构拓展——单元整体复习课的备课经历和思考中学数学参考（中旬）2019（6）.