基于AC-CNN模型的过程故障识别

衷路生，吴春磊

(华东交通大学 电气与自动化工程学院，江西 南昌 330013)

0 引 言

近年来，计算机技术的不断发展，传统数据驱动的故障诊断方法已经无法适应新时期工业“大数据”特性的故障诊断需求[1,2]。然而深度学习模型在工业界使用率不断提高，并且在许多传统的识别任务上识别准确率和效率也得到了大幅度提升[3,4]。在传统故障诊断方法中，文献[5]提出了基于过程监控和故障诊断(PM-FD)的基本数据驱动方法，其提出的多种测试方法能够处理流程中具有较宽操作范围的过程变量的动态问题并且在非高斯测量噪声的情况下，PM-FD的能力也表现优异。文献[6]提出了基于随机优化的变量选择方案来进行识别，其过程中最小化测试数据的累积误差和所选变量的数量，从而减少故障检测时间。文献[7]提出了基于EM聚类的无监督局部多层感知器模型。所提出的方法可以区分不同的已知故障类别，但不能同时诊断多个故障。另外，贝叶斯[8]和深度置信网络[9](DBN)的故障诊断方法，故障识别率低，仍然具有一定的局限性。上述几种方法虽都一定程度上改善故障诊断对TE过程的性能，但是对故障变量特征提取效率低，同时分类故障数量较少且故障识别率仍然较低等问题。

为了提高故障识别的正确率和可靠性，本研究提出一种具有非对称卷积核(asymmetric convolutions)的CNN的工业过程故障识别方法，借鉴文献[10]的思想，引入非对称卷积核模型对重构后的输入故障变量进行充分的特征提取，结合标准的CNN建立AC-CNN模型来识别在线的各类故障测试集样本，得到各类故障测试集样本的识别率和训练时间。最后，进行TE[11](Tennessee Eastman)过程的数值仿真实验，对比标准CNN故障模型及已有文献的故障识别率，验证了该方法在工业过程故障识别中的有效性和优越性。

1 基于非对称卷积核的CNN的故障识别模型

本节提出非对称卷积核模型，并结合标准的CNN网络模型建立AC-CNN故障识别模型；最后，实现故障的精确识别。

1.1 标准的卷积神经网络(CNN)故障识别模型

CNN由特征提取和分类两部分组成。特征提取，包含输入层、卷积层、池化层，其中卷积层和池化层是网络中逐层堆叠的特征提取器。分类包含全连接层和输出层。其中完全连接的图层接收最后一个池化层获得的特征作为输入并执行分类任务。

假设输入层接收待分类n×n的故障数据，然后，卷积层检测输入的局部特征并将它们存储为特征映射。如图1所示，输入层和卷积层之间的连接由卷积核m×m建立。卷积核是一个权重矩形矩阵，其大小远小于输入。特征图包含的每个节点都连接到由卷积核定义的特定输入区域。

图1 数据重构

1.1.1 卷积层输出

卷积核沿水平和垂直轴横跨输入区域，则用卷积核m×m对n×n的工况故障数据Xnew进行步幅S1卷积运算后得到的神经元输出为

y=σ(x*k+b)

(1)

(2)

其中，k(u,v) 表示卷积核k第u行、第v列对应的元素，x(g,g) 的意义同k(g,g)。b∈R是偏置项参数。式(1)、式(2)中的非线性函数σ(·) 有多种类型，比如：σ(t)=tanh(t)， sigmoid函数σ(t)=(1+e-t)-1， relu函数σ(t)=max(0,t) 等，本文主要采用sigmoid函数。

1.1.2 池化层输出

池化层通常位于卷积层之后，主要通过选择位置特征不变来压缩特征映射，并且利用池化层来提取池化块内像素的最大值(max-pooling)、平均值(mean-pooling)。其中通过最大池化和平均池化处理卷积层输出Cp得到输出如式(3)、式(4)所示，当采用步幅S2的最大池化层和平均池化时，可得

Sq(i,j)=max{Cp(S2i-u,S2j-v)},i,j=1,…,Cp/S2

(3)

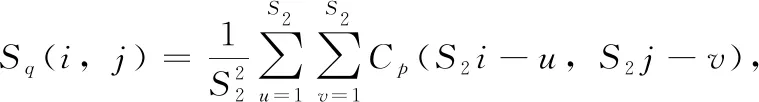
(4)

其中， (u,v) 表示卷积核第u行、第v列对应的元素，Cp表示第p个特征图卷积输出，Sq表示第q个特征图池化输出。

1.1.3 构造目标函数

(5)

1.2 非对称卷积核模型

卷积核是卷积神经网络(CNN)的基础和重要组成部分。对工业过程一维的故障变量数据构建卷积核，先采用将其转换为二维数据如图1所示，然后，为生成的类似矩形图像形状属性配置卷积核，提出非对称卷积核模型(asymmetric convolutions)。与传统CNN使用对称(如 2×2 卷积)核不同，所提出的非对称(2×1)的核形状，以更好地配置二维输入特征数据的几何变化。具体过程如图1所示。

由图1可知图中K为观测变量，每个变量有N个观测值，按照数据重构的方法对观测变量进行二维重构得K1Kb=J1Jd(I(J1Jd>I)或KaKb=JcJd(I(JcJd=I)， 即将二维的数据变成三维矩阵J×I×N。

1.2.1 采用非对称卷积核减少权重参数的个数

如图2(a)所示，在卷积过程中，标准卷积核K1虽然拥有建模矩形形状的能力，但是K1卷积一维数据时，会消耗4个权重参数去建模2个像素的输入特征，并且如果输入特征更加细长或者离散，会浪费更多的权重参数导致建模效率下降。如图2(b)所示，2×2的对称卷积核可以转换得到一个新的非对称(2×1)的卷积核形状。K2卷积一维数据时，只需通过消耗2个权重参数去充分建模2个像素的输入特征，大幅度提高建模效率。

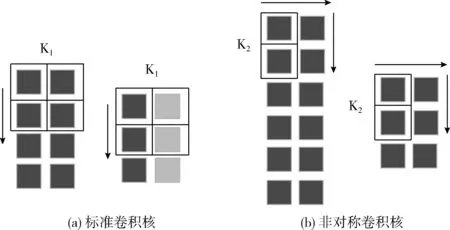
图2 不同卷积核的卷积过程

1.2.2 采用非对称卷积核减少卷积层总参数量

假设对于13×4×100的重构后不规则故障数据 (13×4表示数据维数，100是通道数)，期望利用卷积神经网络得到200个通道的输出，卷积核参数(大小2×2，步幅1，填充1)，采用图3(a)、图3(b)两种卷积模型架构(图中括号内数字表示输出通道数)，其参数量分别为：图3(a)的一般卷积方法：卷积层参数量：100×2×2×200=80000。图3(b)的非对称卷积(卷积核为2×1)方法，卷积层总的参数量：100×2×1×200=40000。

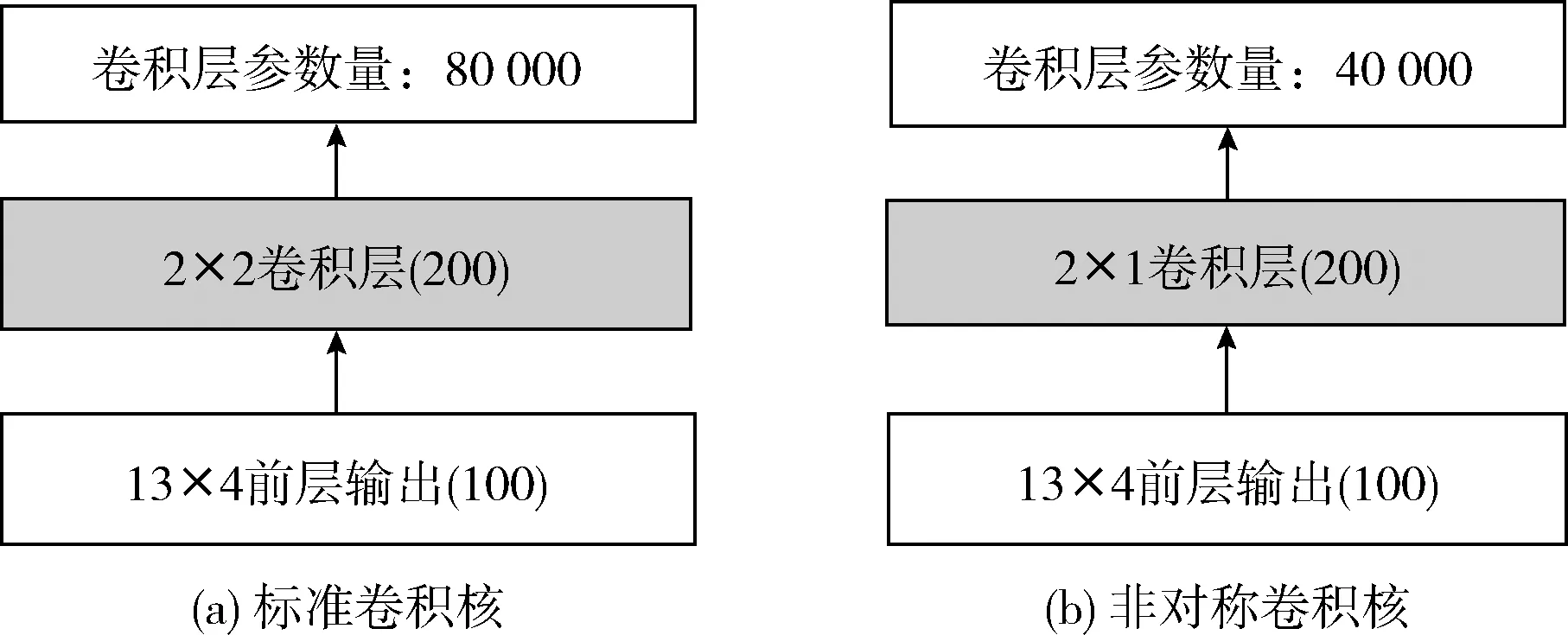
图3 卷积核模型架构

由图3(a)、图3(b)可知：通过设计合适的非对称卷积层输出通道，卷积层总的参数量由80 000降至40 000，大幅度减少了模型参数量。通过不同卷积核模型架构对故障1(关于故障1的详细说明见第2小节的“仿真分析”部分)进行训练并识别，得到的每个epoch平均时间见表1。

表1 不同模型架构的训练时间

综上所述，采用非对称卷积核即减少权重参数的个数也减少卷积层总参数量，并由表1可以看出，提高了训练效率。

1.3 AC-CNN的故障识别模型建立

利用非对称卷积核的CNN模型(AC-CNN)对工况故障识别过程如下。

1.3.1 离线数据训练

步骤1 从故障数据样本集X中随机选取训练集，然后对训练集进行数据预处理得到二维数据X2D∈RP×Q×N其中P、Q为二维数据尺寸，N为样本个数；

步骤2 初始化AC-CNN网络各层的权值、阈值以及学习率，并给出网络的目标输出向量(标签)；

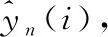
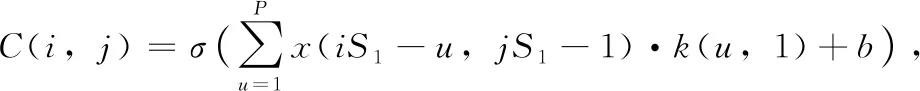
(6)

图4 非对称卷积输出过程

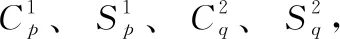
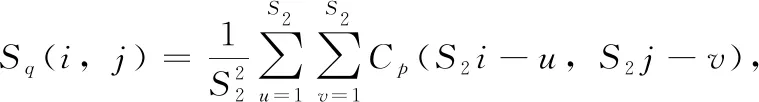
(7)

其中， (u,v) 表示卷积核第u行、第v列对应的元素，Cp表示第p个特征图卷积输出，Sq表示第q个特征图池化输出，S2为运行步幅。

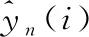
步骤6 由网络的误差反向传播过程计算各权值的调整量Δkn,m、 ΔW和阈值的调整量Δbm、 Δb如下所示；

(1)全连接层的权系数矩阵的偏导数ΔW(i,j) 和偏置项参数的偏导数Δb(i) 如式(8)、式(10)所示

(8)

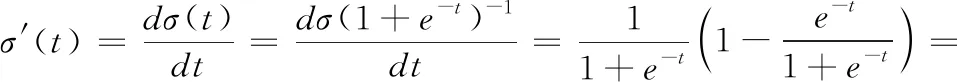
(9)

由式(8)和式(9)可得

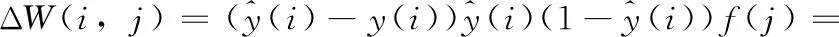
(10)

同理可得全连接层偏置项参数的偏导数Δb(i) 为式(11)所示

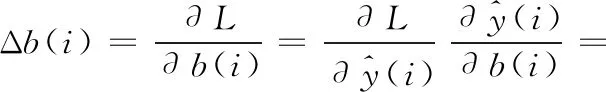
(11)

(2)卷积核矩阵kn,m的偏导数Δkn,m如式(20)所示。其中一个卷积核偏导，为此，在计算积核矩阵kn,m的偏导数之前，先计算矩阵拉直连接、池化层涉及的偏导数

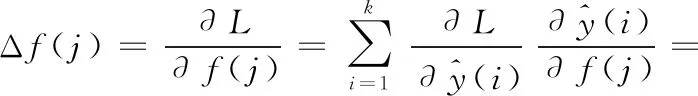
(12)

即由式(12)可得

(13)

又由全连接层的矩阵拉直连接可得，对于h个池化层输出矩阵拉直，连接成一维列向量，记为

f=F({Sm4}m4=1,…,h),f∈Rr×1

(14)

式中：r为全连接层输出的维数。

基于获得的式(13)得到的Δf以及根据式(14)的逆向过程可得到h个池化层矩阵的偏导数

{ΔSm4}m4=1,…,h=F-1(Δf)

(15)

由于池化层没有模型参数，因此根据平均池化原理，利用 {ΔSm4}m4=1,…,h可将误差传播到卷积层输出位置，即

ΔCm3(i,j)=ΔSm4(i,j)

(16)

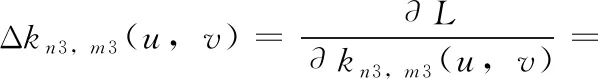
(17)

为了把式(17)的卷积运算统一到卷积定义框架下，分别令

ΔCm3,σ(i,j)=ΔCm3(i,j)Cm3(i,j)(1-Cm3(i,j))

(18)

xn3,rot180(u-i,v-j)=xn3(i-u,j-v)

(19)

则由式(17)、式(18)、式(19)得

Δkn,m=xn,rot180(u-i,v-j)*ΔCn,σ(i,j)

(20)

其中，式(19)中算子rot180表示对矩阵元素旋转180度，式(20)中ΔCn,σ(i,j) 为卷积层误差。

(3)卷积层偏置项参数bm的偏导数Δbm如式(22)所示，其中一个偏置的导数为Δbm3

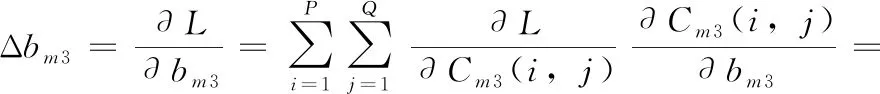
(21)

则卷积层偏置项参数bm的偏导数

(22)

步骤7 获得模型参数的偏导数之后，更新权值和阈值如式(23)所示

(23)

式中：η为学习率，W、b为全连接层权重和偏置项参数，bm、kn,m为卷积层偏置项参数和卷积核矩阵；

步骤8 当经过M次迭代后，判断指标是否满足精度要求，若不满足，则返回步骤3，继续迭代；若满足，训练结束。

1.3.2 在线数据测试

步骤1 从故障数据样本集X中去除训练集后剩余样本作为测试集，然后对测试集进行数据预处理得到二维图像数据XT2D；

步骤2 将XT2D输入已经训练好的AC-CNN网络，从输入层经过逐级的变换得到输出向量，然后对输出向量和测试故障标签数据分别应用max函数，比较两个max函数的输出结果，统计出结果相同的个数，将其与测试集样本个数求百分比即为故障识别率，验证网络的有效性；

步骤3 采集工业过程中实时运行状态下的样本数据并对数据做预处理；

步骤4 将预处理后的实时运行数据输入已经训练好和测试良好的CNN网络，得出各类故障状态的概率，哪种状态概率越大，则可以快速准确地判定运行过程中的故障类型。

2 仿真分析

为了说明提出的基于非对称卷积核的CNN的工业过程识别方法的性能，本节在TE平台进行数值仿真实验分析，利用训练后的AC-CNN模型来识别测试集样本故障类别，得到各类故障测试集样本的识别率；最终实现故障识别。

2.1 AC-CNN网络模型参数的设置

TE仿真平台是一个开放的、具有挑战性的化工模型仿真平台，具体过程请参见文献[12]，如图5所示。其中TE过程包括12个操作变量和41个测量[12,13]，本文采用两种选择方式：选取52个变量和49个变量，据此采取将故障变量转换成二维图像的处理方法得到13×4矩形图像和 7×7 方形图像。在模拟故障工况时，分别进行了48 h的运行模拟，每隔3 min采样一次，采集21种故障运行时的960个样本，故障均在样本点161时引入，则选取后800个样本作为训练集和测试集，其中随机选取750个样本作为训练集，剩余50个样本或采集在线运行的数据作为测试集，利用训练得到的AC-CNN模型，进一步对测试集进行故障识别。

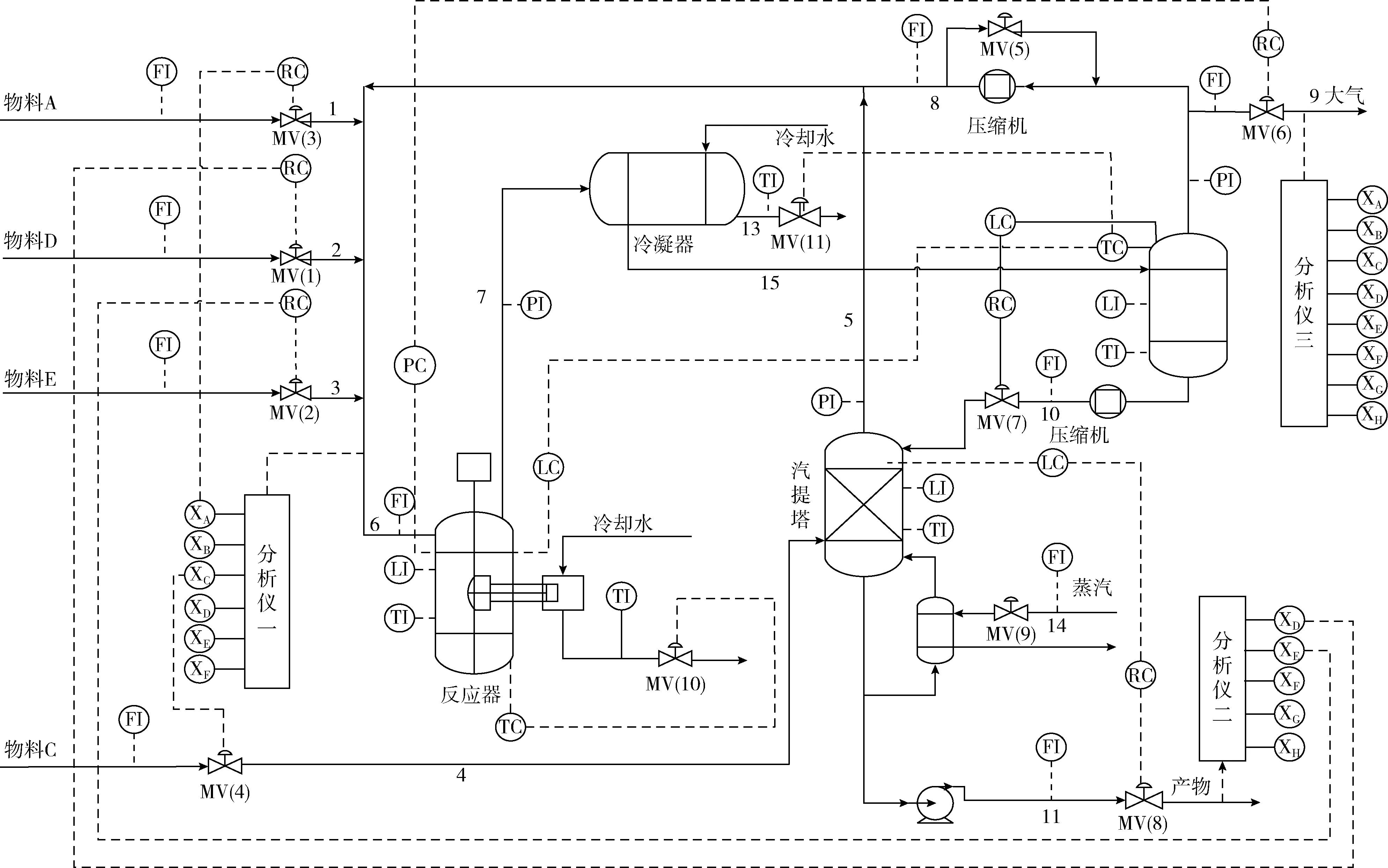
图5 TE过程的流程

为了体现故障变量与卷积核匹配的重要性，本文提出4种深度卷积神经网络模型，其网络模型见表2，然后选择表2中识别率最高的AC-CNN模型作为最终的网络模型。模型训练涉及的参数主要包含输入层故障变量重构情况、每个卷积层的滤波器数量和卷积核尺寸。

表2 深度卷积神经网络模型

表2的4种深度学习模型的训练还有学习率和批量大小需要进行优化。学习率表示深度学习模型的连接权重的更新速度，本文学习率的取值范围是(0,1)。批量大小是用于一次权值更新的训练数据量，数值越低，权值更新越频繁，并且模型训练需要更多时间。考虑到预处理后的训练数据集的大小为750×4×21=63000，本文将批处理大小设置为100,50和20(对应于每个训练迭代权值更新频率分别为630,1260和3150)，同时记录每次训练迭代的模型训练性能。模型训练的结果表明，4种模型的学习率为0.9，批量大小取为50，各模型具体结构见表2。

2.2 故障识别结果

根据建立的AC-CNN和已有的标准CNN模型，依据表2的各网络模型参数，得到模型1和模型4对故障1的训练误差结果如图6所示，即AC-CNN模型和标准CNN模型的训练误差。

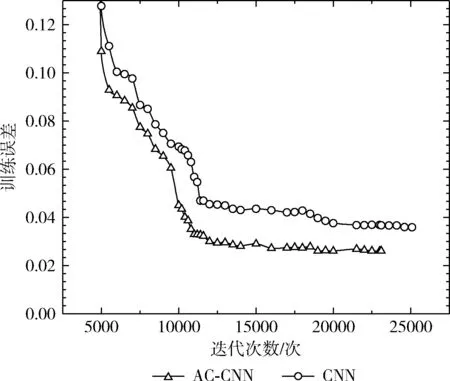
图6 模型训练误差

由图6可知：AC-CNN模型迭代结束到23 000次时的训练误差比标准的CNN模型的对应值低了约1%。

利用63 000个训练集样本建立表2的深度学习模型，然后用1050个测试集来评估所建立的深度学习模型，进而得到4种模型对于21种故障测试正确率(识别率)以及训练时间见表3。其中模型4(AC-CNN模型)的故障识别率的混合矩阵如图7所示。

表3 各模型故障识别率

由表3可见模型4即AC-CNN模型21种故障的平均识别率达到88.67%，另外，从表3也可以看出本模型的故障平均识别率比其它3种模型分别高出4.86%、5.05%、5.81%，且AC-CNN模型(模型4)每个epoch平均训练时间较其它3种模型分别缩短了0.129 s、0.243 s、0.329 s，又由图7的AC-CNN模型的21种故障识别率的混合矩阵也可看出，本文提出的故障诊断模型使各类故障的识别性能和效率得到了显著提高。

图7 AC-CNN模型的故障识别率的混合矩阵

为了更好地理解AC-CNN模型，对实验结果利用可视化技术，通过可视化随机选取11类故障的测试集所有样本，在原始数据、CNN与AC-CNN模型全连接层的特征表达经过t-SNE[14]降成3维后的分布，如图8所示。

由图8可以看出，工况采样数据经过AC-CNN模型操作之后，各类故障己经可以很好的区分，这表明AC-CNN区分故障信号的能力很强，第7类与第8类故障在CNN模型分类后的依然特征表达线性不可分，但随着AC-CNN模型使用之后，两类故障的特征表达线性可分，这说明AC-CNN模型的增强了非线性表达能力。综上， AC-CNN通过非对称卷积使用，将不可分的特征映射到非线性可分空间，也验证了AC-CNN模型非对称卷积核的设计思想的合理性和优越性。

对比已有文献故障识别率得出不同故障诊断方法的性能比较见表4：(a)基于PM-FD模型[5]；(b)基于PCA的优化变量选择模型[6]；(c)基于EM聚类的监督式局部神经网络模型[7]；(d)基于多模过程的贝叶斯模型[8]；(e)基于深度置信网络模型[9]；(f)基于AC-CNN模型(本文提出的)。具体表现如图9所示。

所有21种故障的故障识别结果见表3，平均故障识别率为88.67%。取前20种故障与文献中的故障诊断模型(见表4)相比，本文提出的故障诊断模型的性能得到了显着提高，特别是Fault13和Fault15。根据表4，Fault13的故障识别率达到98%，尤其在故障15被认为是最难识别的故障之一，在之前的文献报告中的故障识别率都低于30%，而在本文提出的方法，故障15的识别率可以达到70%。另外，由图9和图7可以看出Fault15 和Fault16两种故

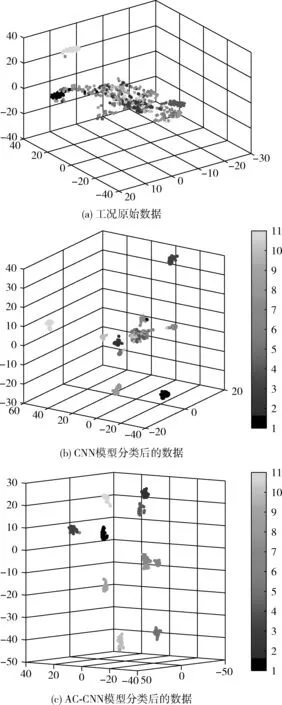
图8 数据经过t-S NE可视化之后的分布

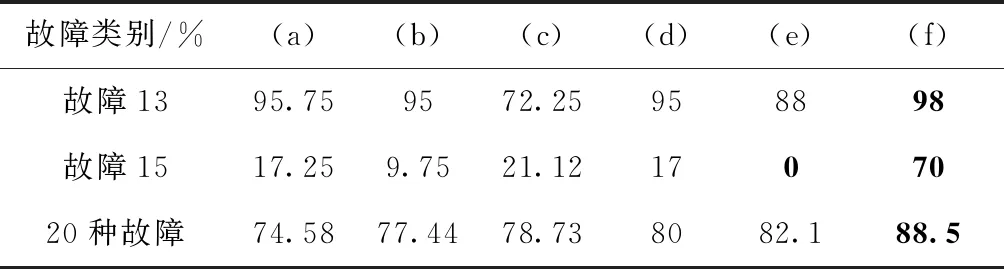
故障类别/%(a)(b)(c)(d)(e)(f)故障1395.759572.25958898故障1517.259.7521.121707020种故障74.5877.4478.738082.188.5

障特征相近，而已有文献的抽象方法是基于空间域中开发，对故障变量没有充分提取，本文从时域出发，对数据进行预处理，通过非对称卷积核配置重构变量充分提取故障特征，从而可以看出，在这两种故障标签偏离正常状态比其它故障要轻得多情况下，本模型的故障识别能力依然有较好的表现。

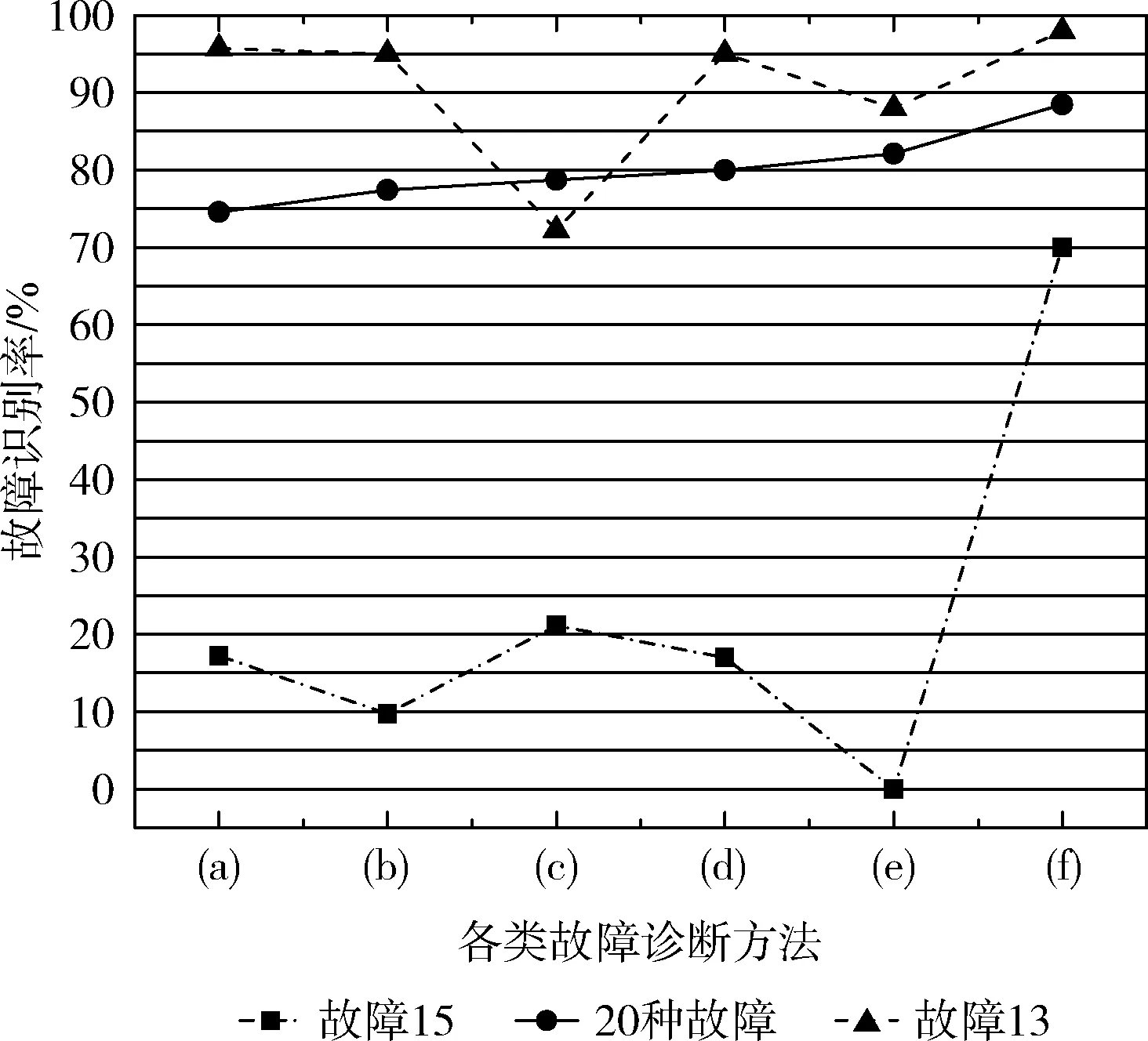
图9 故障识别率对比

3 结束语

针对复杂工业过程中故障变量特征，并同时识别多类故障，提高识别性能，本文提出了一种具有AC架构的CNN模型。研究了基于对称卷积核的CNN改进得到非对称卷积核的AC-CNN模型，根据4种模型的故障诊断结果生成全面的故障识别结果。其中改进的基于AC-CNN的故障识别模型在TE过程中的应用表现出色，明显优于其它3种模型的平均故障诊断率和训练时间，而在20种被广泛研究的故障中，与其它故障诊断方法报告的平均故障识别率相比，也表现突出，大幅度降低了计算复杂度并提高了识别率。TE过程实验结果表明：所构造的基于AC-CNN的故障识别模型优于已有的故障识别模型，在故障发生时，能实时准确判断出的故障类型，大大降低了复杂工业过程中的故障诊断成本。

尝试通过调整超参数和模型部分结构，探索AC-CNN模型其它工业故障实时分类标注问题的应用，是笔者下一步的工作。