一种全局参数估计的水下主动偏振去雾算法

于洪志，孙春生，胡艺铭

（海军工程大学 兵器工程学院，湖北 武汉 430033）

引言

水下光学成像具有重要的应用价值，但也具有挑战性[1]。受水体及水中粒子等散射介质影响，在水下拍摄的图像存在目标模糊及对比度低等问题，难以对图像进行利用和分析[2]。

根据文献[3]和文献[4]，人们主要将对比度作为判断图像质量的依据。关于获得高对比度水下图像的技术大体可分为两类：一类是基于数字图像处理技术，主要是水下图像增强[5-7]与水下图像复原[8-10]；另一类是基于成像系统，主要是水下距离选通系统[11]、水下结构光成像系统[12]等。受海洋动物利用偏振信息来改善视觉[13]的启发，水下偏振成像技术作为一种解决问题的新思路被提出来。近几十年的相关研究表明，通过偏振技术可以抑制成像中的后向散射光，并通过成像算法的后处理进一步克服后向散射光对图像质量的影响。

Schechner 将大气中的偏振去雾算法思想[14]应用到水下，该方法[2]采用被动光源进行水下目标成像，利用偏振差分成像得到复原图像，算法过程简单、处理耗时短、易于实现，但模型中的全局参量通过人机交互选取一个常量来代替。Treibitz[4]重建了在主动光照明条件下的水下偏振成像模型，该算法在不同海域中获取的正交偏振图像的后处理中进行了验证，均取得了较好的实验效果，但算法中将后向散射光的偏振度视为常量，导致复原的水下图像有可能出现明暗不均的情况。Li[15]在Schechner 的研究基础上加入图像增强作为预处理，依然得到了理想的水下去雾图像，但仍没有考虑后向散射光偏振度为全局变量这一因素。此外，还有采用圆偏振照明的水下偏振成像去雾技术[16]。

为解决现有算法中对参数估计不佳的问题，依据实际课题背景，本文采用主动偏振光进行照明，首先对正交的偏振图像进行图像增强预处理，通过分析水下主动偏振成像模型，推导出后向散射光偏振度特征参量，利用多项式拟合函数估算出全局变量的后向散射光偏振度，再迭代求解出相对于最优图像质量的目标反射光偏振度，最终得到水下去雾图像。通过实际的水下偏振成像实验进行验证，结果表明，本文算法与现有算法相比，可提高图像对比度，丰富图像信息，为水下目标探测和识别提供支持。

1 水下主动偏振成像模型

在水下成像时，探测器接收到的辐射信号有2 个来源。第1 个是场景目标的辐射，其辐射在水中被吸收和散射减弱，称为目标反射光；第2 个是环境照明，环境光经过水中粒子的多次散射照射到探测器上，称为后向散射光[1]。水下图像的数学表达式为

式中：I(x,y)为水下成像系统获得的图像；S(x,y)为目标反射光，该信号实际由2 个分量组成，分别为直接透射光和前向散射光；B(x,y)为后向散射光。

目标反射光包含了水下目标受到水体吸收前的辐射信息（即为直接透射光），又包含了直接透射光向前传播时与介质互相作用而产生的前向散射光，吸收和前向散射均使得图像模糊。前向散射光在水下近距离成像时对图像质量影响较小，因此本文忽略前向散射光的因素。后向散射光是由主动照明光与介质发生多次散射作用而形成的背景光，如图1 所示。由于主动光源照度的不均匀性，后向散射光实际是不均匀的。如前所述，对比度影响着图像质量，导致对比度下降的主要原因是后向散射光，因此水下去雾算法就是克服后向散射光引起的“影响”。

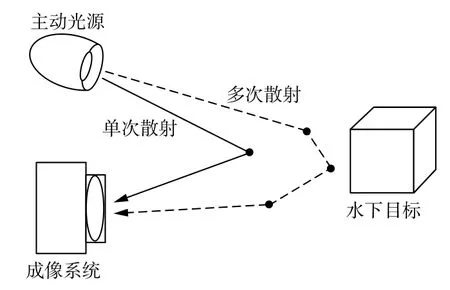
图1 散射过程示意图Fig.1 Schematic diagram of scattering process

利用偏振成像系统，得到光强度最大和最小时的2 幅偏振正交图像，其强度分别记为Imax(x,y)和Imin(x,y)，则由式（1）可推得：

式中：Smax(x,y)和Bmax(x,y)为偏振成像系统接收到目标场景“最亮”时的目标反射光和后向散射光的强度。同理：

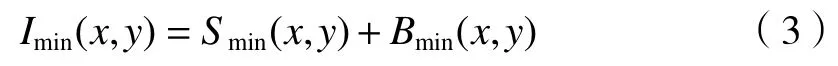
根据米氏散射规律，后向散射光为部分偏振光，因此后向散射光偏振度为

对目标反射光作为非偏振光还是部分偏振光，以往有不同的看法，文献[2]和[3]认为随着传输距离的增加，目标反射光偏振态的影响在图像中的比重降低；文献[17]认为对于一些退偏度低的目标，其目标反射光的偏振态不能忽略。此模型考虑了这两种情况，因此目标反射光偏振度为

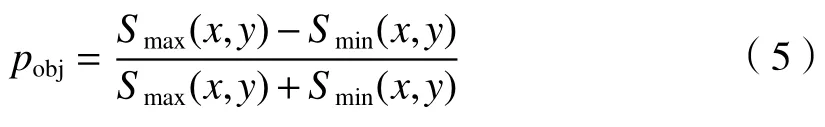
下面为表达方便，省略了坐标量（x，y）。由（2）式和（3）式可得到总光强I为

由（2）式～（5）式可得到：

最后，联立（6）式和（7）式，求解得到目标反射光分量S和后向散射光分量B：

经过理论推导可知，在给定后向散射光偏振度pscat和目标反射光偏振度pobj的情况下，就可从2 张正交偏振图像中分离出后向散射光分量，目标反射光分量S即为复原图像。

2 预处理与全局变量的估计

2.1 偏振图像的预处理

本步骤借鉴文献[15]的算法思想，对正交偏振图像进行预处理，旨在拉伸正交偏振图像的直方图。首先，通过直方图拉伸处理偏振图像Imin(x,y)。直方图拉伸的数学表达式如下

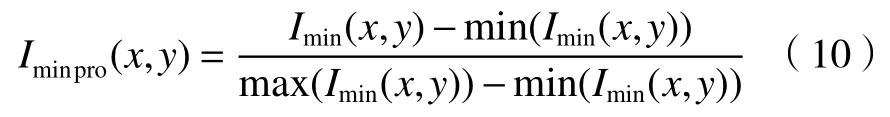
式中：Iminpro(x,y)是经过处理后的偏振图像；Imin(x,y)是原图像；min(Imin(x,y))是原图像中灰度值最小的像素点；max(Imin(x,y))是原图像中灰度值最大的像素点。根据偏振度定义，正交偏振图像的偏振度为

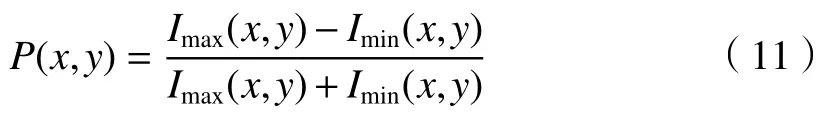
根据公式（11），正交偏振图像之间的偏振关系可以通过偏振度P(x,y)表示为

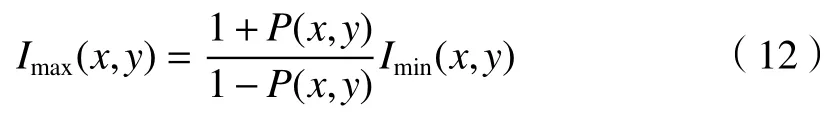
因此，根据公式（10）和（12）得到Imax(x,y)的拉伸图像：

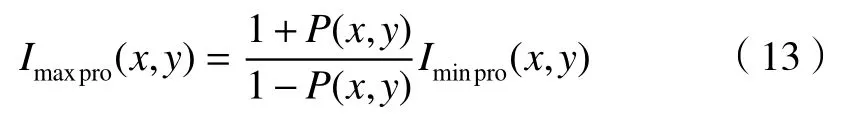
通过直方图拉伸处理的2 张正交偏振图像的偏振度与2 张原始正交偏振图像的偏振度相同，如果直接拉伸2 张正交偏振图像的直方图，则该偏振特性无法保证。此外，由于混浊水体介质的退偏性大，“最暗”的图像Imin(x,y)比“最亮”的图像Imax(x,y)受到更少（除光学系统遮蔽外）的后向散射光的影响，目标反射光信息在Imin(x,y)里占比更大，因此，可以认为直接对偏振图像Imin(x,y)进行处理更为有效。

2.2 全局变量pscat 的估计

现行算法对后向散射光偏振度的估计是基于手动所选的区域值，近似地将后向散射光偏振度作为常量来处理。为提高去雾算法的稳定性，避免复原图像出现明暗不均的现象，本文重新分析了后向散射光偏振度，将其视为全局变量，并利用二元多项式函数进行数据拟合，拟合过程是基于最小二乘法。

不同物体具有不同的偏振特性，如石块的退偏性较强，金属的退偏性较弱[18-19]。当目标反射光的偏振特性不可忽略时，无法直接利用偏振图像估算目标处后向散射光偏振度，但可以依托于目标周围区域的后向散射光偏振度的数据，通过二元多项式函数来估算目标处的后向散射光偏振度的值。实验表明，后向散射光偏振度pscat受主动光源的影响，在整张图像上确实是有变化的，如图2 所示。因此本文将后向散射光偏振度作为全局变量来处理是合理的。

图2 偏振度图Fig.2 Schematic diagram of polarization degree

将偏振图像的后向散射光偏振度值设为关于（x，y）的二元多项式函数，以图像左下角为原点建立三维坐标系，像素点分别为x轴和y轴，偏振度值为z轴，则二元多项式拟合函数数学表达式为

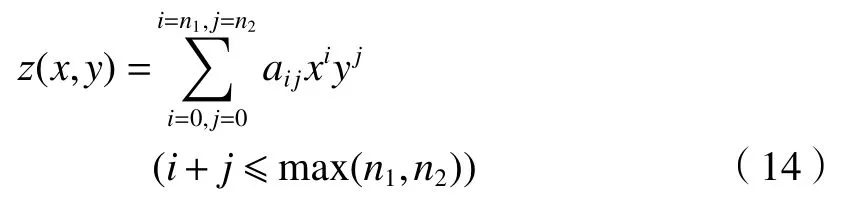
式中：n1为x的最高阶数；n2为y的最高阶数。将（14）式展开推导，即：

以上线性方程组写成矩阵形式：

因为方程组无解，要找到一组所设的二元多项式系数a00,a10,···,an10,a01,···,a0n2,ai j，使平方偏差

最小。经推导，二元多项式系数所满足的代数方程为

因此，系数最优解为

由此得到二元多项式拟合函数，可估算出全局变量的后向散射光偏振度。

关于x与y阶数的确定，以决定系数R2为依据进行迭代求得。决定系数R2可用来判断拟合函数的解释力，其正常取值范围为0～1，决定系数越接近1，表明拟合函数的解释能力越强，即对数据拟合也越好。决定系数R2定义为回归平方和SSreg与总平方和SStot的比值，数学表达式为

z假设后向散射光偏振度中包括z1,···,zn，共n个观察值，相对应的拟合值分别为f1,···,fn，则平均观察值为（20）式中回归平方和SSreg为，总平方和SStot为

2.3 目标反射光偏振度pobj 的确定

本文将目标反射光也视为部分偏振光。通过水下主动偏振成像模型可知，目标反射光的偏振度为

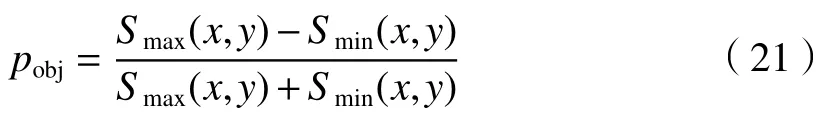
由（8）式可知，目标反射光偏振度pobj对目标反射光分量S的影响比重较小，将目标反射光偏振度作为全局变量处理意义不大，而且会增加算法的复杂性。为适应实际应用的要求，通过迭代法选取一个相对于水下图像质量的最优pobj值。为此，采用图像增强测量值[15,17,20]（the value of measure of enhancement，EME）来量化图像质量。EME 的数学表达式为

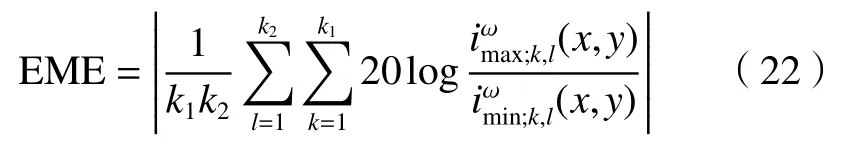
式中，数字图像按像素被划分成k1×k2个单位块，其二维序号为（k，l），为序号为（k，l）的ω块中的最大灰度值和最小灰度值。通过迭代搜索来求取EME 最大化的目标反射光偏振度pobj，继而得到图像质量最优的去雾图像。

3 实验结果与分析

在实际的水下场景中进行成像实验，验证算法的可行性，实验装置如图3 所示。光源为连续光谱LED 光源，光束发散角为35°～37°，波长范围为435 nm～656 nm，照明装置内置线偏振片。成像系统是Teledyne DALSA 公司的Genie Nano M2450 偏振相机，相机的传感器是Sony 公司的IMX250MZR CMOS 单色传感器，该相机可输出一张同时包含4 个偏振方向（0°；45°；90°；135°）的灰度图像，输出图像的分辨率为2 464×2 056 像素。实验中，在PMMA 水箱中将清水和牛奶混合，使水浑浊以达到改变水体介质的目的。实验目标为目标靶（材料如表1 所示）和钢索，如图4 所示。

图3 实验装置示意图（俯视视角）Fig.3 Schematic diagram of experimental device (top view)

表1 目标靶对应位置材料Table 1 Target corresponding position materials

图4 实验目标Fig.4 Experimental target

将PMMA 水槽（1 180 mm×580 mm×310 mm）注满清水，在清水中加入1 000 μL 染料墨水和4 000 μL全脂牛奶改变水体介质。实验过程中，主动光为唯一光源，避免其他杂散光干扰。调整光源和相机，使得相机0°偏振传感器方向获得的结果“最亮”。拍摄实验目标，成像系统获得一张含有正交偏振关系的原始合成图像，如图5 所示。子图像中，偏振方向0°的图像为光强度最大的图像Imax，偏振方向90°的图像为光强度最小的图像Imin。在该水体条件下，原始图像的对比度低，图像中目标靶及钢索细节处无法有效识别。

图5 原始图像Fig.5 Original image

在计算机上进行图像处理验证本文算法。从原始图像中得到图像Imin和图像Imax（分辨率1 232×1 028 像素），并对两正交偏振图像进行预处理，原偏振图像及预处理后的偏振图像如图6 所示。根据本文算法，对偏振图像进行处理，得到水下去雾图像，如图7 所示。与强度图像相比，处理后的图像中目标靶的轮廓信息更加明显，淹没的信息得以重现，图像对比度得到改善，表明该算法可以去除后向散射光对水下成像的影响，改善水下图像质量。

图6 原偏振图像和预处理后的偏振图像Fig.6 Original polarized image and preprocessed polarized image

图7 强度图像和处理后的图像Fig.7 Intensity image and processed image

通过二元多项式拟合出的后向散射光偏振度如图8(b)所示。x的阶数为2，y的阶数为3，决定系数R2为0.909 7。对比图8(a)和图8(b)可知，拟合函数依托于目标周围区域的后向散射光偏振度，估算出目标处的后向散射光偏振度，去除掉目标反射光的偏振特性影响，实现将后向散射光偏振度作为全局变量。目标反射光偏振度pobj取值0.1，EME 达到最大值，取值示例如图9 所示。

图8 偏振度图和后向散射光偏振度拟合图Fig.8 Polarization degree diagram and backscattering light polarization degree fitting diagram

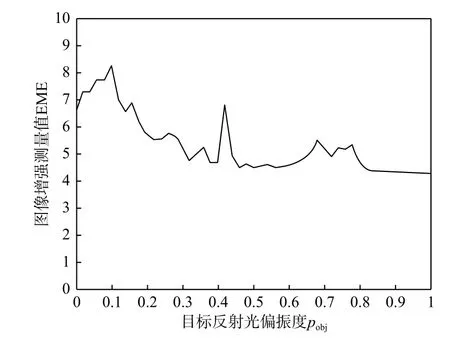
图9 目标反射光偏振度取值示例Fig.9 Example of target reflected light polarization degree value

利用图像增强测量值EME 和直方图对处理后的图像进行评估，将本文算法与其他算法处理的水下图像进行对比分析，如图10 所示。其中，图10（a）为强度图像，图像受后向散射光的影响，目标与背景之间对比度下降，图像质量受到很大影响；图10（b）为Schechner 方法处理得到的图像，该方法在非均匀主动光照明条件下适用性降低，由于将后向散射光特征参量作为常量处理，使得处理后的图像中出现失真现象；图10（c）为Treibitz 方法处理得到的图像，该方法建立偏振主动成像模型，手动取一块背景区域作后向散射光特征参量，处理后的图像出现了明暗不均的现象；图10（d）为Li 方法处理得到的图像，该方法为经典Schechner 方法的延展，预处理虽然提升了图像对比度，但也使后向散射光特征参量增大，处理后的图像中失真现象更加明显；图10（e）为本文算法处理得到的图像，将后向散射光偏振度作为全局变量处理，可以有效地解决复原图像的明暗不均及失真现象。从EME 值来看，图10（e）的EME 值较以往算法约提高70%；从直方图来看，图10（e）的直方图灰度值分布范围更宽广且相对均匀，意味着图像的对比度更大；从主观视觉来看，图10（e）克服了明暗不均和失真的现象，图像质量最优。通过对比分析，可看出本文算法和以往算法相比有一定的提高和改善。

图10 各算法处理的图像及其直方图对比Fig.10 Comparison of images processed by each algorithm and histograms

本文还采用两种常用的客观评价参数对实验图像进行比较，如表2 所示。对比结果表明，本文算法处理的图像依然具有优势，与主观评价和EME 参数评价结论相同。

为证明本文算法在不同浓度介质中的普遍适用性，在相同实验条件下加入1 000 μL 染料墨水和6 000 μL 全脂牛奶。如图11 所示，与上述实验相比，由于介质浓度增大，强度图像中后向散射光的影响也随之增加，经过本文算法处理的图像表现出更高的对比度，图像质量优于强度图像，证明本文算法适用于不同浓度的介质，图像处理效果稳定。

表2 各算法的客观评价参数Table 2 Objective evaluation parameters of each algorithm

图11 强度图像和处理后的图像Fig.11 Intensity image and processed image

4 结论

本文在发散型主动光照明的实验条件下，通过建立水下主动偏振成像模型，提出一种基于二元多项式拟合函数的后向散射光参数估计算法，并有效结合图像增强技术作为预处理，设计实验进行了算法的验证。实验结果表明，本文算法可以改善后向散射光对水下图像质量的影响，提高图像对比度，图像复原效果较以往算法相比有一定的提高，几种客观评价参数均有优势，直方图灰度值分布更广，且对于不同浓度的介质，算法有良好的复原稳定性。与此同时，本文算法受限于光源视场范围和图像噪声，图像噪声与后向散射光偏振度和目标反射光偏振度紧密相关，复原图像的直方图中像素点曲线波动变大，说明在处理的过程中噪声也被放大，这些问题还有待进一步讨论。