采用3D几何特征的草莓叶片含水率监测与试验验证

符凯娟，冯　全，杨　森，陈佰鸿

采用3D几何特征的草莓叶片含水率监测与试验验证

符凯娟1，冯全1※，杨森1，陈佰鸿2

（1. 甘肃农业大学机电工程学院，兰州 730070；2. 甘肃农业大学园艺学院，兰州 730070）

为实现植物水分状况的实时在线监测，该研究采用非接触式双目摄像仪获取草莓叶片的深度图像并转换为点云数据，从中抽取叶片三维（Three-Dimension, 3D）形态信息，用以建立草莓叶片含水率的预测模型。采用随机采样一致算法与整体最小二乘法相结合的点云平面拟合方法拟合叶片平面从而获取叶倾角，采用代数拟合球面法以估计叶片的拟合球半径，从而可以定量分析草莓叶片的几何参数与不同含水率的关系。在建模集的一元线性回归分析中，叶倾角与叶片含水率、余弦值与叶片含水率、球半径与叶片含水率均线性相关，决定系数分别为0.842 9、0.854 6 和 0.880 8；采用多元线性回归分别分析了球半径和叶倾角、球半径和叶倾角的余弦值与叶片含水率，两者与叶片含水率之间关系都十分显著（<0.001），修正决定系数分别为0.914 3和0.912 9。对所建立的单变量含水率预测模型和双变量预测模型在验证集上进行了验证，结果表明，利用球半径和叶倾角建立的回归模型预测叶片含水率效果最好，均方根误差仅为0.015 8，决定系数达0.953 4。该试验研究结果可以快速检测草莓叶片含水情况，为草莓含水状况的非接触式测量提供一种有效的方法，为农情信息精准获取提供技术支持。

水果；模型；图像处理；草莓；平面拟合；球面拟合；叶片含水率

0 引 言

叶片是植物重要组成部分，叶片含水率检测与估计方法众多，基于图像处理的方法大多利用二维图像中植物叶片投影面积和颜色空间进行研究。江朝晖等[1]采用偏最小二乘回归建立了越冬期小麦冠层图像特征与冠层含水率检测模型，检测得到冬小麦品种冠层含水率检测模型的相对误差均值为1.29%。Han等[2]采用信息灰度共生矩阵和灰度直方图分析抽穗期玉米叶片与含水率的关系，研究得到叶片颜色特征均值与含水率的关系，模型决定系数为0.701 7。王方永等[3]分析棉花颜色参数，并发现棉花颜色参数G-R与含水率及含水率指数相关性最好，以G-R建立了棉花含水率及含水率指数预测模型。然而二维图像特征方法受光照、气温以及植物品种等影响大，无法精准预测植物叶片含水率[4]。

近年来，利用三维信息研究农作物生长状态的技术已经越来越成熟。三维信息通常采用点云表示，点云是同一空间参考系下表达目标空间分布和目标表面特性的海量点的集合，在农业上可以用来表现作物的外观形态[5-7]。王勇健等[8]在黄瓜、玉米和葡萄叶片利用点云的配准、简化以及去噪的操作基础上，进行了三维建模，得到植物叶片网格模型，精确度得到了提高；Azzari等[9]通过建立点云的凸包构建结构关系实现网格化建模；吴升等[10]建立椭球分层的点云密度收缩方法实现果树冠层叶片器官点云分离，利用邻近传播主成分分析算法实现叶片特征参数的求解，利用Laplacian收缩算法实现冠层骨架点的连通，实现了果树冠层叶片的三维快速自动重建；张伟洁等[11]提出一种基于三维点云的苹果树叶片结构形态三维重建方法，普适性较好。植物叶片在不同含水条件下表现出的几何形态有所变化，为利用三维点云研究叶片水分提供了生理基础。萎蔫是植物亏水胁迫环境下表现出的一种生命特征，研究者利用三维点云计算的特征参数研究了植物叶片萎蔫状态[12-14]。张慧娟等[15]和蔡祥等[16]应用激光扫描装置获取植株3D图像，分别定义了4种植物萎蔫指数，前者通过检验自定义的4种萎蔫指数发现叶片边缘投影求和平均萎蔫指数具有更好的鲁棒性，后者通过比较4种萎蔫指数刻画萎蔫状态的相关性，两两间决定系数>0.736。也有学者对植物叶片生态指标与植物叶片倾斜程度与植物叶片含水率的直接关系进行了研究。Font等[17]通过研究叶片和茎缘在引力条件下的倾斜状态，计算叶和茎倾斜状态时的夹角判断植物含水率；何东健等[18]基于玉米节间高度、叶片长度以及株高等参数，建立基于单一参数的玉米水分胁迫预测模型，提出了一种基于多视角立体视觉的玉米水分胁迫预测模型。

作物在缺水状态下其叶片的几何形态会随之发生变化，出现萎蔫现象，通过测量这些变化可能监测到作物含水率的变化。植物表观的3D信息可以通过激光扫描、相机多视角重建等方式采集，激光扫描精度虽高，但需要人机交互，过程较繁琐，数据采集速度较慢。而基于双目图像重建作物表观模型获取三维信息方法虽然精度略低，但操作方便，采集速度快。本研究通过对在不同水处理下草莓叶片几何形态的测量，建立了叶片几何参数与叶片含水率的预测模型。为了测量叶片几何参数，使用双目主动结构光技术获取叶片图像深度图，将其转化为3D点云，重构出3D草莓表观，采用3D实例分割技术分割出草莓叶片，对叶片进行平面和球面拟合，用拟合平面的法向量和球半径分别表示叶片整体的倾斜和卷曲程度，以反应草莓在缺水时的表观形态变化。由于采用双目主动结构光技术获取深度数据，其精度较高，且无需人机交互，使得本方法可以实现图像采集、3D重构以及几何参数计算等测量过程的自动化，为植物叶片缺水状态监测提供了高效、定量化观测方法。该方法也可以用在与植物表观状态相关的表观3D建模、农作物生长状态监测、产量估计等领域，是一种非接触、快捷和实用性高的监测手段。

1 材料与方法

1.1 试验材料

1.1.1 供试品种

供试对象为结果期的盆栽草莓，品种为宁玉，土壤质地为草炭和珍珠岩接近质量比为1:1的混合，底肥充足。草莓叶片椭圆形，叶面粗糙，耐热耐寒性强，冬季不易矮化，春季转暖不易疯长；由于盆栽草莓叶位简单，叶片稀疏且交叉生长，同一根茎生成三复出叶，上下叶片重叠部分少，适合于三维条件下的叶片含水率监测研究。

1.1.2 仪器设备

试验使用MYNTAI公司（美国）开发的D1000-IR-120/Color室内型双目摄像仪获取叶片深度图，该相机基线为120.0 mm，焦距为2.86 mm，分辨率为1 280× 480像素，外观尺寸165 mm×31.5 mm×30.12 mm，支持红外线（Infrared Ray, IR），且IR可探测距离为3 m。该相机融合了双目和结构光测量的优点，可以获取低纹理对象的深度图像。MYNTAI公司提供了基于C++编程语言的软件开发工具包（Software Development Kit, SDK），同时提供彩色和深度图像输出，使得图像的采集简单易行。使用型号为SM-110的电子秤获取花盆质量。使用精度为0.000 1 g的分析天平和型号为YHG-300-S的远红外快速恒温干燥箱获得草莓叶片含水率。

1.2 试验方法

1.2.1 试验设计

本试验在甘肃农业大学（甘肃兰州）实验室内进行，研究时间为2019年10月。试验过程中控制实验室内温湿度不变，准备生长状态基本相同的49盆正常生长的草莓，标记为1～49。试验过程中将49盆草莓分为7组，每组7盆草莓，其质量基本相同为1.383 kg，将每组7盆草莓中的5盆作为试验建模组，剩余2盆作为试验验证组。试验前将每盆草莓灌水至饱和，然后称重并记录，将水分蒸发导致的质量损失作为控制参数，第1组到第5组控制参数分别设置为10%、20%、30%、40%、45%的质量损失，其余2组为持续干旱和持续饱和组，每4 d浇一次水，并分别记录7组中每盆草莓质量。试验期间，每日下午5点对每盆草莓进行称重，称重结果与相应控制条件进行比较，若达到控制条件，则该盆草莓在此条件中继续生长3 d，在此期间，每天进行称重和补充水分，控制该盆草莓质量不变。试验发现，损失10%质量平均需要4 d时间，而损失45%质量约15 d时间。当一盆草莓质量达到相应水分散失控制条件并继续生长3 d后，在第4天对该盆草莓拍照并测量其叶片含水率。持续干旱组和持续饱和组试验同步完成，待干旱组草莓叶片表现明显萎蔫时，对干旱组和饱和组草莓进行拍照，并测量叶片含水率。

1.2.2 叶片含水率测定

选择每盆草莓顶层叶片大容易观察的5个茎秆，以每1个茎秆中的三复出叶的中间叶片为样本测定叶片含水率来代替整株草莓的叶片含水率。均匀剪下盆栽草莓顶层的5片叶子，并放在铝箔中使用分析天平称重，记录鲜质量（1, g），然后放置在远红外快速恒温干燥箱内进行干燥，干燥温度为80 ℃，干燥时间约为1 h，干燥过程中每15 min称重一次，称重到叶片质量误差<0.000 4 g时，记录此时的叶片质量（2, g），可通过计算得到叶片含水率leaf（%），如（1）式所示：

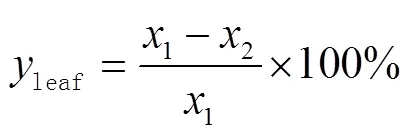
1.2.3 模型评价指标

本研究采用3个指标对叶片含水率预测模型精度进行评估：均方根误差（Root Mean Square Error, RMSE）、平均相对误差（Average Relative Error, ARE）和决定系数（coefficient of determination,2），指标计算公式如式（2）、式（3）和式（4）所示：

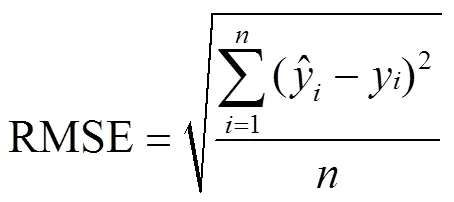
2 点云叶片处理

2.1 叶片点云获取与分割

2.1.1 叶片点云获取

图像采集在实验室内进行，一般使用太阳自然光源，阳光不足时利用室内光源补光，拍摄时间为早上9:00－10:00。图像采集时，利用三脚架将双目摄像仪固定，使得镜头朝下，镜头光轴垂直于地面，盆栽草莓位于双目镜头正下方。采集的植物彩色（Red-Green-Blue, RGB）图像以.jpg格式存储，3D点云彩色图像以.ply格式储存，从而得到植物重构模型（图1）。第1组至第5组草莓植株30°视角下的3D点云重构图像样例如图2所示。

注：图1c中蓝色线条表示坐标轴z，绿色线条表示坐标轴x，红色线条表示坐标轴y。

图2 不同质量损失水平下的草莓三维重构图像样例

2.1.2 叶片点云分割

由分割难易程度将点云分割分为语义分割和实例分割两大类，语义分割是给点云中的每个点预测一个带有语义的类别标签，而实例分割是在此基础上将场景中的单个对象进行分割[19-22]。为了计算每片叶子的几何参数，本研究的草莓叶片采用实例分割。使用了三维语义实例分割（Three Dimensional Semantic Instance Segmentation, 3D-SIS）的神经网络，从几何和颜色信号中实现精确的实例预测，该网络首先用二维卷积提取每个像素的二维特征，然后将得到的特征向量投影到三维网格中，将二维（Two-Dimension, 2D）和3D特征学习相结合，使得对象检测和实例分割的精度大大提高[23]。利用该分割方法可以精确分割出草莓点云图中的叶片部分，分割效果显著。分割时选取测定叶片含水率的5片叶子（图3 a），分割后叶片图像样例如图3 b所示。重复分割方法，将盆栽草莓中所标记叶片全部分割，分割结果以.ply格式保存在计算机中。

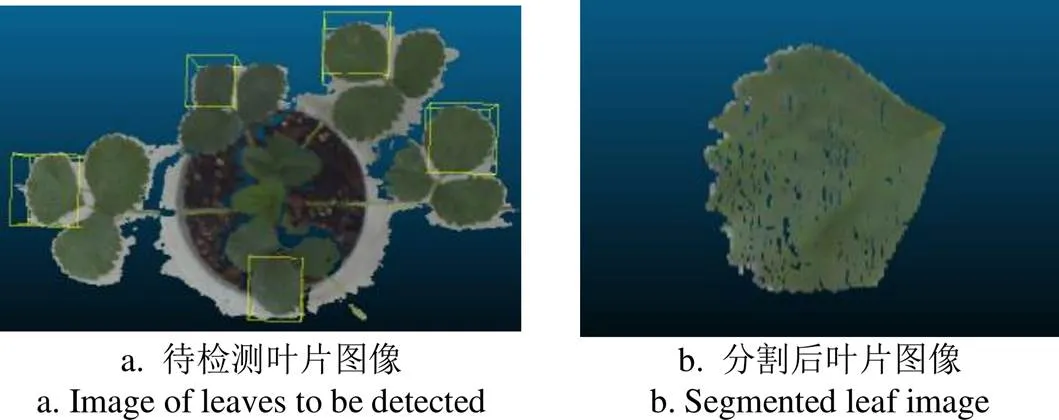
注：图3a矩形框中叶片是人工标记的需要被检测和分割的叶片。

2.2 叶片几何特征提取

作物在缺水状态下，其叶片形态发生变化，主要体现在叶倾角和卷曲程度变化。叶倾角通常是测量叶柄和茎杆的夹角而获得，但草莓无主茎，无法采用该方法获得。本研究在得到草莓叶片点云后，对每片叶片采用平面拟合和球面拟合，用拟合平面法向量与水平面的夹角作为叶子倾斜程度的表征，称作叶倾角（°），而将拟合球面的半径作为叶子整体卷曲程度的表征，称作球半径（，cm）。这2个特征与叶片位置、大小无关。

2.2.1 叶片平面拟合

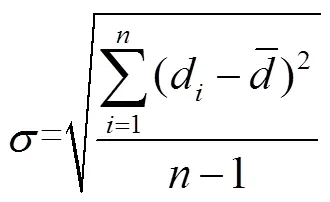
该拟合方法拟合效果显著，平面拟合均方根差小于 0.003，能很好地剔除异常值并减小误差，当异常值较多时，该方法也能保持稳健性，拟合效果显著。得到叶片拟合平面后，由内积法计算拟合平面法向量，规定法向量朝向为水平面以上，叶片拟合与法向量俯视图、前视图、右侧视图分别如图4所示。

注：矩形框为叶片拟合平面；箭头为拟合平面法向量的方向。

2.2.2 叶片球面拟合

球面拟合方法主要分为几何法和代数法。几何法主要利用所有采样点到拟合球面的距离平方和最小，主要使用线性化迭代最小二乘求解，缺点是容易出现迭代发散或导致局部最优的情况[26]。代数法则是根据采样点建立隐函数，其零等值面即为拟合球面，该方法计算简单、速度快且适合平面模型[27-28]。

本研究中草莓叶片近似平面模型，即使叶片缺水萎蔫，也没有达到极度弯曲，故使用代数法对叶片进行球面拟合，由三维点云数据建立球面表达式如式（7）所示：

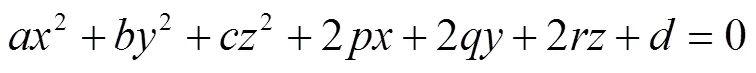
式中为球半径，cm；、、为该球面表达式的参数。

然后由点云数据的三维坐标构建矩阵如式（8）所示，计算矩阵T，以及矩阵最小的特征值对应的特征向量，该特征向量即为系数向量={,,,,,,}的向量值，通过计算向量得到球面表达式的系数，从而得到球半径。

球面拟合均方根误差小于0.003，拟合误差小，拟合效果显著，拟合球面俯视图、前视图、右侧视图如图5所示。

3 结果与分析

3.1 试验结果

3.1.1 叶片含水率

经计算得到各组叶片含水率，其变化趋势如图6所示。其中，饱和组7盆草莓叶片含水率全部达到最高，叶片含水率最高可达85.13%。随着盆栽草莓质量减少，水分蒸发增大，叶片含水率依次减小，叶片含水率最小为61.10%。

图6 饱和组、干旱组和不同质量损失水平下的叶片含水率变化趋势图

3.1.2 叶倾角与球半径

采用随机采样一致算法与整体最小二乘法相结合的点云平面拟合方法计算出每盆草莓的每片分割叶片叶倾角，但同一盆草莓中个别叶倾角与其他叶片叶倾角相差很大，若采用叶倾角均值则易受离群点的影响，故本试验使用分割后的5片叶片的中值代表这一盆栽草莓叶片的叶倾角（表1），其中叶倾角实测值数据是通过FARO（美国）公司生产的法如便携式测量臂（型号为FARO Forensic Laser Scan Arm）扫描得到，该实测数据可与本研究计算数据进行比较。由表1可知，叶片球面拟合可得叶片球半径，其中球半径数值均为每盆草莓分割出来的5片叶片球半径的中值，球半径实测值数据获得方法跟叶倾角实测数据方法相同。由表1结果数据可知，随着叶片质量损失增大，叶片叶倾角和球半径的实测值与计算值同步减小，叶倾角实测值由69.0°减小到25.3°，计算值由68.0°减小到22.0°，球半径计算值和实测值在饱和组达到最大，实测值由1.882 7 cm减小到0.214 0 cm，计算值由1.869 7 cm减小到0.213 9 cm。

3.2 草莓叶片含水率与3D几何参数关系的一元回归分析

3.2.1 叶倾角与叶片含水率之间的关系

为了定量研究草莓叶倾角和球半径的变化而引起叶片含水率的变化，提取建模组中分割后草莓叶片的叶倾角，并计算得到叶斜角的余弦值，利用EXCEL回归分析叶倾角与其余弦值对不同含水率情况下的草莓叶片不同程度的影响。

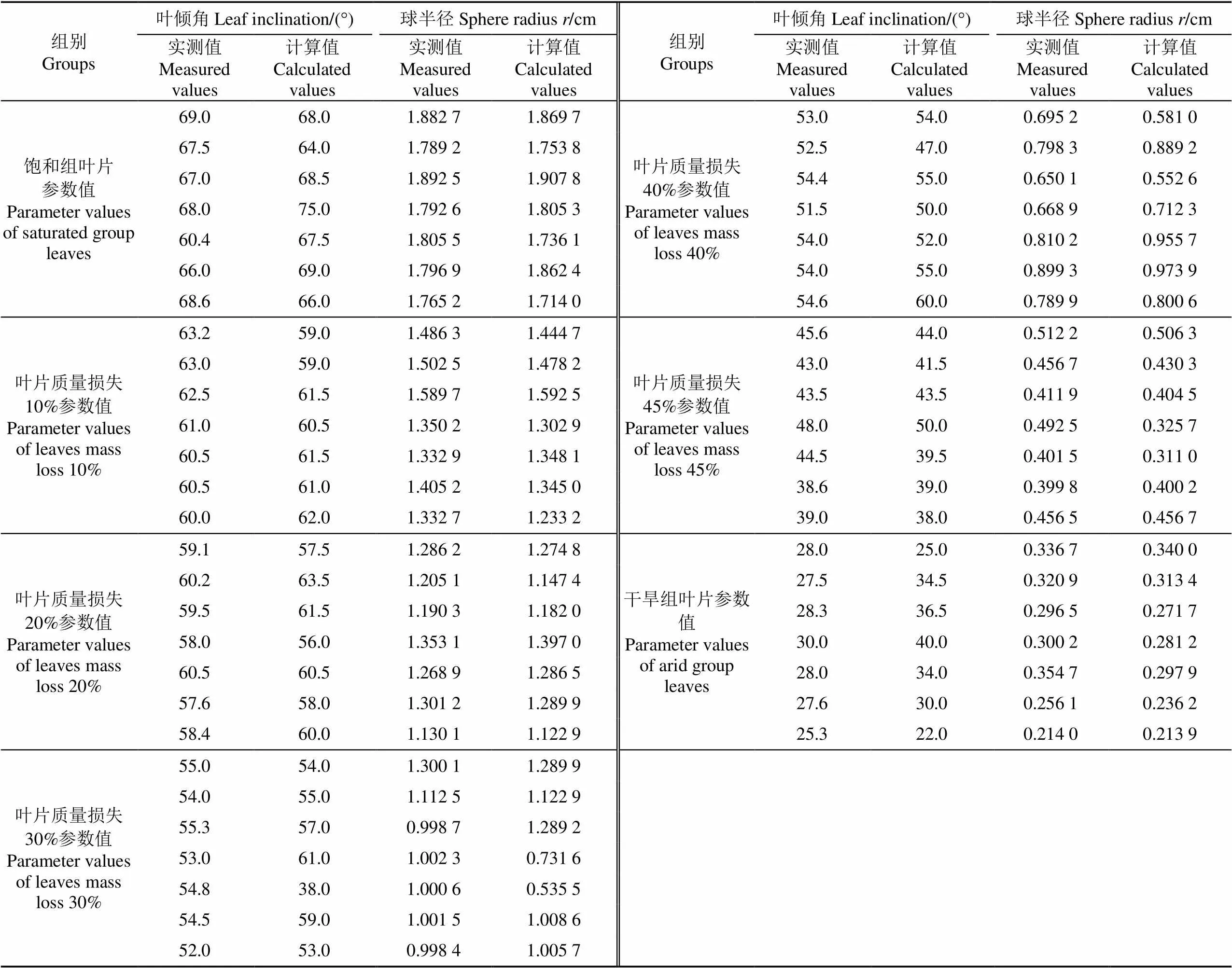
表1 草莓叶片参数叶倾角与球半径

叶倾角与叶片含水率的回归结果如表2所示，其中叶倾角与叶片含水率之间决定系数为0.842 9，说明叶倾角与叶片含水率之间具有显著的相关性。由表2可知，叶倾角回归系数标准误差为0.022 8和0.000 4，表明该参数具有很高的精确度，利用回归表统计中的系数，得到叶倾角与叶片含水率的预测模型为angle=0.005 6angle+0.438 5，式中angle为变量叶倾角，(°)；angle为叶倾角对应的叶片含水率。该模型拟合效果如图7a所示。

本研究也计算叶倾角余弦值作为叶片倾斜程度的特征量，利用同样的方法分析叶倾角余弦值与叶片含水率之间的关系（表2）。由表2可知，叶倾角余弦值与叶片含水率之间具有显著的线性相关性，同样达到了极显著性检验水平，决定系数为0.854 6，略高于叶倾角，得到余弦值与叶片含水率的预测模型为cos=−0.422 9cos+ 0.983 7，式中cos为变量余弦值；cos为叶倾角余弦值对应的叶片含水率。该模型拟合效果如图7b所示。

表2 叶片含水率与叶片几何参数一元回归统计

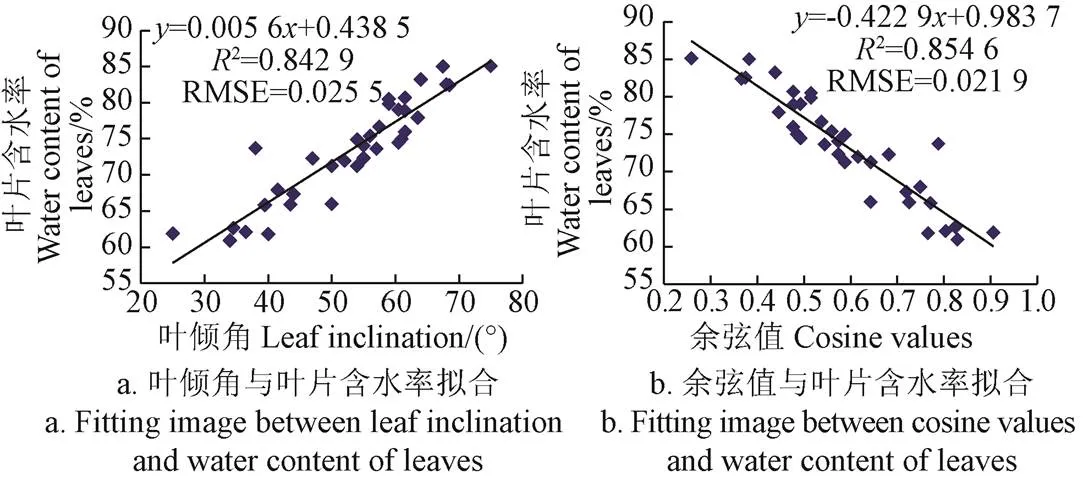
图7 叶倾角、余弦值与叶片含水率拟合效果图

3.2.2 球半径与叶片含水率之间的关系

提取建模组中分割后草莓叶片的球半径，利用线性回归的方法对叶片球半径与叶片含水率进行回归分析（表2）。由表2可知，球半径与叶片含水率之间的决定系数达0.880 8，标准误差为0.024 8，在3个参数中标准误差最小，决定系数最高，具有显著的线性相关性，可得球半径与叶片含水率之间的预测模型y=1.229x+0.612 7，式中x为变量球半径，cm；y为球半径对应的叶片含水率。该模型拟合如图8所示。

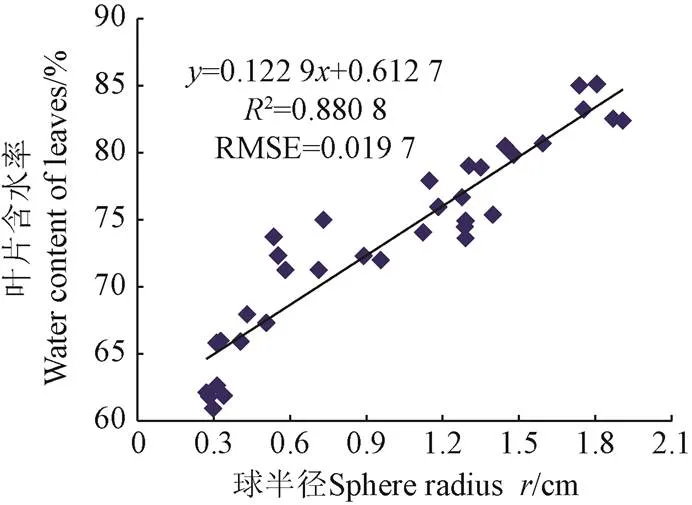
图8 球半径与叶片含水率拟合效果图

3.3 草莓叶片含水率与3D几何参数关系的多元回归分析

为了找到最优预测模型，对叶倾角和球半径、叶倾角余弦值和球半径进行多元回归分析，由于自变量个数的增加，导致模型拟合效果过高，故采用修正决定系数（Adjusted coefficient of determination,Adj2）衡量多元回归（表3）。

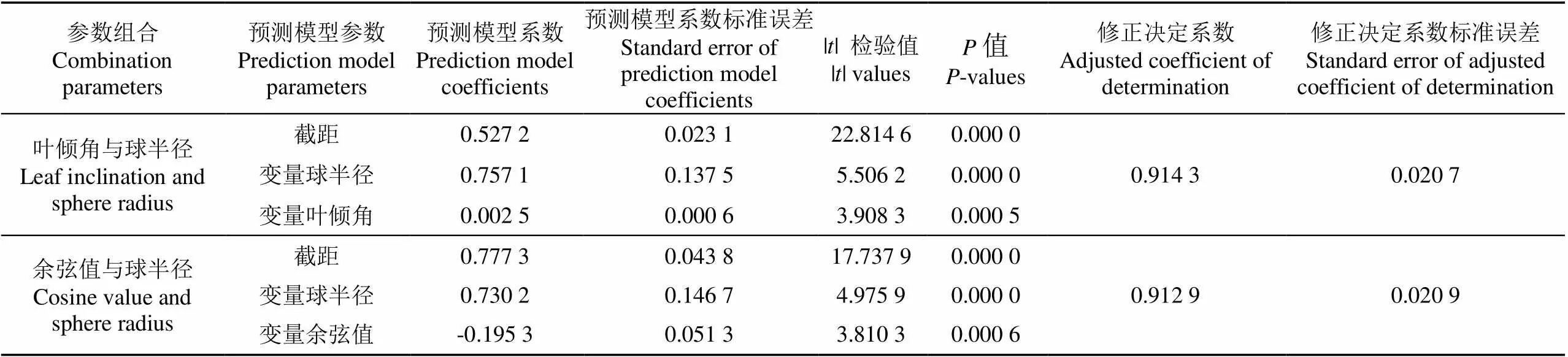
表3 叶片含水率与叶片几何参数多元回归统计

3.3.1 叶倾角和球半径与叶片含水率

通过对叶倾角和球半径与叶片含水率进行多元回归分析发现，修正决定系数为0.914 3，修正决定系数标准误差为0.020 7，说明自变量叶倾角和球半径与因变量叶片含水率之间的关系显著（=0.000 5）。由表3可知，可得叶倾角和球半径、叶片含水率之间的预测模型为1=0.757 1r+ 0.002 5angle+0.527 2，式中1为自变量叶倾角和球半径对应的叶片含水率。

在得到球半径和叶倾角、叶片含水率之间的预测模型后，利用偏回归系数的检验法判断自变量叶倾角和球半径对叶片含水率的影响程度的大小。在多元线性回归中，可直接由||值的大小判断因素主次顺序。由表3可知，球半径和叶倾角对应的||检验值分别为5.506 2和3.908 3，根据||值大小，因素的主次顺序为球半径、叶倾角。值表示检验偏回归系数不显著的概率，由表3可知，变量球半径对试验结果影响比变量叶倾角显著（<0.01）。

3.3.2 余弦值和球半径与叶片含水率

利用同样的方法分析余弦值和球半径与叶片含水率之间的关系，由表3可知，修正决定系数为0.912 9，标准误差为0.020 9，说明自变量余弦值和球半径与因变量叶片含水率之间关系显著。自变量余弦值和球半径与叶片含水率之间的关系极其显著（<0.01），预测模型系数为0.777 3、0.730 2、−0.195 3，即叶倾角余弦值和球半径、叶片含水率之间的预测模型为2=0.730 2r−0.195 3cos+0.777 3，式中2为叶倾角余弦值和球半径对应的叶片含水率。表3中球半径和叶倾角余弦值对应的||检验值分别为4.975 9和3.810 3，根据||值大小可知因素主次顺序为球半径、余弦值，说明变量球半径对试验结果更重要。

在Kacira等[29]、王娟[30]和孙燕等[31]的研究中，提出用植物冠层投影面积预测植物含水率，而冠层投影面积取决于叶片的倾斜程度与叶片的卷曲程度。曲率越小，叶片弯曲程度越大，则投影面积减小，同样，叶片倾斜角越小，叶片表现为耷拉状态，则投影面积越小。本试验只选取草莓植株顶层的三复出叶的中间叶片进行测量，这类叶片的区分性好，少有遮挡，单个叶片分割效果好，3D重构后叶片较完整清晰，这是计算叶倾角和拟合球半径的基础。但实际中可能会遇到更多复杂情况，一种常见的情况是叶片密集，上下叶片重叠，导致下层叶片无法完整重构，本研究认为从顶层易检测的叶片估计出的含水率在一定程度上能够反映出整株草莓的含水情况，这对于算法要求较低，仅需检测出顶层特定叶片即可，便于本方法的应用。下层或其他叶位叶片姿态是否与水分变化有较强的相关性以及算法如何精准检测并完整分割出特定叶片也是本试验未来研究的内容，从自动数据采集和处理角度看，需要更为精细的3D标检测算法和实例分割算法配合。本试验结果表明，对草莓叶片，代表叶片卷曲程度的拟合球半径对叶片水分预测要比叶片倾斜角更为敏感，在植物冠层投影面积预测水分时起到了更为重要的作用。

3.4 草莓叶片含水率预测模型的评估

以验证组14盆草莓叶片为验证样本，利用模型评价指标对建立的草莓叶片含水率预测模型进行精度检验，结果如表4所示。由该模型评价结果可知，双变量预测模型预测含水率的效果明显优于单变量预测模型，由表4可知，5个模型的RMSE和ARE值均小于0.1，其中，双变量含水率预测模型1的RMSE和ARE的值为0.015 8、0.018 7，在5个模型中达到最小，且该预测模型决定系数2为0.953 4，表明由叶倾角与球半径建立的双变量叶片含水率预测模型可以较好地预测草莓叶片含水率。

表4 草莓叶片含水率预测模型评价

注：angle为变量叶倾角，(°)；angle为叶倾角对应的叶片含水率；cos为变量余弦值；cos为叶倾角余弦值对应的叶片含水率；x为变量球半径，cm；y为球半径对应的叶片含水率；1为自变量叶倾角和球半径对应的叶片含水率；2为余弦值和球半径对应的叶片含水率。

Note:angleis the variable leaf inclination angle, (°);angleis the leaf water content corresponding to the leaf inclination angle;cosis the variable cosine values,cosis the leaf water content corresponding to the cosine values of leaf inclination;xis the variable sphere radius, cm;yis the leaf water content corresponding to the sphere radius;1is the leaf water content corresponding to the variable leaf inclination angle and sphere radius;2is the leaf water content corresponding to the cosine values of leaf inclination and the sphere radius.

4 结 论

直观上看植物含水率的变化会对其叶片几何形态产生影响，故通过对叶片几何形态的测量可能估计出叶片的含水率。本研究采用双目成像技术重构叶片的三维（Three-Dimension, 3D）形态，计算叶片点云的拟合平面方向和拟合球半径作为指示叶片几何形态变化的参数，试验表明，利用这些参数预测叶片含水率是可行的。经过模型检验发现，叶倾角和球半径的双变量预测模型相比其他模型可以更满意地反映出草莓叶片含水情况。本试验后期对“丰香”草莓也进行了试验，结果发现采用球半径与叶倾角的双变量水分预测模型的方法对于其他品种草莓叶片同样有效。借助叶片3D参数实现植物早期缺水情况的辨识，对于精细灌溉控制有潜在的工程应用前景。利用回归建立的叶片含水率预测模型，对于草莓叶片亏水胁迫信息的准确解析，在生态与作物保护领域也具有一定的应用价值。本研究利用不同含水情况下的盆栽草莓进行分组试验，得出主要结论如下：

1）采用非接触的方式提取草莓植株3D图像，对图像中的草莓叶片进行分割，通过随机采样一致算法与整体最小二乘法相结合的点云平面拟合方法技术，计算叶片平面拟合的法向量，作为叶片叶倾角，采用代数拟合球面法提取了叶片的拟合球半径以反映叶片弯曲程度，建立了基于两种参数的单变量与双变量草莓叶片水分预测模型，其中球半径与叶倾角的预测模型决定系数达0.953 4，可很好预测草莓叶片含水率。

2）本研究通过定点拍摄的草莓深度图像得到草莓植株的重建3D模型，相对于传统的激光扫描仪采集植物3D数据，本方法操作简单，人机交互环节少，可以实现参数提取自动化，从而极大提高了数据采集和处理的效率。

[1]江朝晖，杨春合，周琼，等. 基于图像特征的越冬期冬小麦冠层含水率检测[J]. 农业机械学报，2015，46(12)：260-267.

Jiang Zhaohui, Yang Chunhe, Zhou Qiong, et al. Detection of canopy water content of winter wheat during wintering period based on image features[J]. Transactions of The Chinese Society for Agricultural Machinery, 2015, 46(12): 260-267. (in Chinese with English abstract)

[2]Han Wenting, Sun Yu, Xu Tengfei, et al. Dtecting maize leaf water status by using digital RGB images[J]. International Journal of Agriculture and Bioengineering, 2014, 7(1): 45-53.

[3]王方永，王克如，王崇桃，等. 基于图像识别的棉花水分状况诊断研究[J]. 石河子大学学报：自然科学版，2007(4)：404-407.

Wang Fangyong, Wang Keru, Wang Chongtao, et al. Diagnosis of cotton water status based on image recognition[J]. Journal of Shihezi University: Natural Science Edition, 2007(4): 404-407. (in Chinese with English abstract)

[4]吴琼，朱大洲，王成，等. 农作物苗期长势无损监测技术研究进展[J]. 农业工程，2011，1(4)：19-25.

Wu Qiong, Zhu Dazhou, Wang Cheng, et al. Research progress of crop seedling growth non-destructive monitoring technology[J]. Agricultural Engineering, 2011, 1(4): 19-25. (in Chinese with English abstract)

[5]Zhang Yali, Zhang Hongzhi, Du Mingwei, et al. Leaf wilting movement can protect water-stressed cotton (L.) plants against photoinhibition of photosynthesis and maintain carbon assimilation in the field[J]. Journal of Plant Biology, 2010, 53(1): 52-60.

[6]Xiao Boxiang, Wu Sheng, Guo Xinyu, et al. A 3D canopy reconstruction and phenotype analysis method for wheat[C]// Beijing Agricultural Internet of Things Engineering Technology Research Center of China Agricultural University, Changchun, China, 2017.

[7]张雪，郭彩玲，宗泽，等. 基于轮廓分割的草莓叶片三维建模[J]. 农业工程学报，2017，33（增刊1）：206-211.

Zhang Xue, Guo Cailing, Zong Ze, et al. 3D reconstruction of strawberry leaves based on contour segmentation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(Supp.1): 206-211. (in Chinese with English abstract)

[8]王勇健，温维亮，郭新宇，等. 基于点云数据的植物叶片三维重建[J]. 中国农业科技导报，2014，16(5)：83-89.

Wang Yongjian, Wen Weiliang, Guo Xinyu, et al. 3D reconstruction of plant leaves based on point cloud data[J]. Journal of Agricultural Science and Technology, 2014, 16(5): 83-89. (in Chinese with English abstract)

[9]Azzari G, Goulden M, Rusu R. Rapid characterization of vegetation structure with a Microsoft Kinect sensor[J]. Sensors, 2013, 13(2): 2384-2398.

[10]吴升，赵春江，郭新宇，等. 基于点云的果树冠层叶片重建方法[J]. 农业工程学报，2017，33（增刊1）：212-218.

Wu Sheng, Zhao Chunjiang, Guo Xinyu, et al. Method of fruit tree canopy leaf reconstruction based on point cloud[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(Supp.1): 212-218. (in Chinese with English abstract)

[11]张伟洁，刘刚，郭彩玲，等. 基于三维点云的苹果树叶片三维重建研究[J]. 农业机械学报，2017，48（增刊1）：103-109.

Zhang Weijie, Liu Gang, Guo Cailing, et al. Apple tree leaf three-dimensional reconstruction based on point cloud[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(Supp.1): 103-109. (in Chinese with English abstract)

[12]赵燕东，荣斐，刘圣波，等. 基于2DFT的植物叶片萎蔫程度与微环境因素相关性研究[J]. 农业机械学报，2014，45(1)：253-258.

Zhao Yandong, Rong Fei, Liu Shengbo, et al. Correlation between wilting index of plant morphology defined by 2DFT spectrum and micro-environmental factors[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(1): 253-258. (in Chinese with English abstract)

[13]张新，高超，Martin K，等. 基于TOF摄像机的植物叶态萎蔫辨识研究[J]. 农业机械学报，2016，47(5)：275-280.

Zhang Xin, Gao Chao, Martin K, et al. Identification of plant leaf wilting using TOF camera[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(5): 275-280. (in Chinese with English abstract)

[14]张新，赵燕东，郑力嘉，等. 基于三维机器视觉的植物叶片萎蔫预测模型[J]. 农业机械学报，2014，45(9)：260-267.

Zhang Xin, Zhao Yandong, Zheng Lijia, et al. Prediction model of plant leaf wilting using 3-D machine vision[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(9): 260-267. (in Chinese with English abstract)

[15]张慧娟，赵燕东，孙宇瑞，等. 基于3-D图像的植物亏水胁迫萎蔫体态辨识方法[J]. 农业机械学报，2011，42(1)：154-158.

Zhang Huijuan, Zhao Yandong, Sun Yurui, et al. Identification of plant morphology wilt-induced by water stress with 3-D based image[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(1): 154-158. (in Chinese with English abstract)

[16]蔡祥，孙宇瑞，赵燕东，等. 基于3-D数据的叶片萎蔫形态辨识方法[J]. 农业机械学报，2015，46(5)：286-292.

Cai Xiang, Sun Yurui, Zhao Yandong, et al. Identification methods for plant wilting at leaf-scale based on 3-D imaging[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(5): 286-292. (in Chinese with English abstract)

[17]Font L, Körösi F, Farkas I. Leaf inclination based on destructive water stress inclination for vegetables[J]. Acta Horticulturae, 2005, 5(691): 99-106.

[18]何东健，熊虹婷，芦忠忠，等. 基于多视角立体视觉的拔节期玉米水分胁迫预测模型[J]. 农业机械学报，2020，51(6)：248-257.

He Dongjian, Xiong Hongting, Lu Zhongzhong, et al. Predictive model of maize moisture stress during jointing stage based on multi-view stereo vision[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(6): 248-257. (in Chinese with English abstract)

[19]Ioannidou A, Chatzilari E, Nikolopoulos S, et al. A survey on deep learning advances in computer vision with 3D data[J]. ACM Computing Surveys, 2017, 50(2): 1-38.

[20]Ramachandram D, Taylor G W. Deep multimodal learning: A survey on recent advances and trends[J]. IEEE Signal Processing Magazine, 2017, 34(6): 96-108.

[21]顾军华，李炜，董永峰. 基于点云数据的分割方法综述[J]. 燕山大学学报，2020，44(2)：125-137.

Gu Junhua, Li Wei, Dong Yongfeng. Segmentation methods for point cloud: A survey[J]. Journal of Yanshan University, 2020, 44(2): 125-137. (in Chinese with English abstract)

[22]Verdoja F, Thomas D, Sugimoto A. Fast 3D point cloud segmentation using supervoxels with geometry and color for 3D scene understanding[C]// IEEE International Conference on Multimedia and Expo (ICME 2017). Hong Kong, China, 2017.

[23]Hou Ji, Dai Angela, Niener M. 3D-SIS: 3D semantic instance segmentation of RGB-D scans[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake, United States, 2018.

[24]Fischler M A, Bolles R C. Random sample consensus: A paradigm for model fitting with application to image analysis and automated cartography[J]. Communication Association Machine, 1981, 24(6): 381-395.

[25]李希，韩燮，熊风光. 基于RANSAC和TLS的点云平面拟合[J]. 计算机工程与设计，2017，38(1)：123-126.

Li Xi, Han Xie, Xiong Fengguang. Plane fitting of point cloud based on RANSAC and TLS[J]. Computer Engineering and Design, 2017, 38(1): 123-126. (in Chinese with English abstract)

[26]Gander W, Golub G H, Strebel R. Least-squares fitting of circles and ellipses[J]. Bit Numerical Mathematics, 1994, 34(4): 558-578.

[27]Pratt V. Direct least-squares fitting of algebraic surfaces[J]. Acm Siggraph Computer Graphics, 2002, 21(4): 145-152.

[28]李胜男，林晓，陈言，等. 基于点云的球面三维逆向建模[J]. 图学学报，2013，34(3)：49-52.

Li Shengnan, Lin Xiao, Chen Yan, et al. 3D converse modeling for sphere point cloud[J]. Journal of Graphics, 2013, 34(3): 49-52. (in Chinese with English abstract)

[29]Kacira M, Ling P P, Short T H. Machine vision extracted plant movement for early detection of plant water stress[J]. American Society of Agricultural Engineers, 2002, 45(4): 1147-1153.

[30]王娟. 基于计算机视觉的棉花干旱诊断研究[D]. 石河子：石河子大学，2014.

Wang Juan. Study on Drought Diagnosis based on Computer Vision[D]. Shihezi: Shihezi University, 2014. (in Chinese with English abstract)

[31]孙燕，曹成茂，缪鹏程，等. 基于叶片面积的温室植物水分监测系统的设计[J]. 传感器与微系统，2010，29(12)：82-84.

Sun Yan, Cao Chengmao, Miao Pengcheng, et al. Design of moisture monitoring system of plants in greenhouse based on leaf’s area[J]. Transducer and Microsystem Technologies, 2010, 29(12): 82-84. (in Chinese with English abstract)

Monitoring and experimental verification of strawberry leaf moisture content using 3D geometric features

Fu Kaijuan1, Feng Quan1※, Yang Sen1, Chen Baihong2

(1,,730070,;2.,,730070)

Water is indispensable for plant growth, and water shortage will affect the yield, growth, and quality of plants. The rapid and non-destructive detection of water content in plants is of great significance to scientific guidance of irrigation and to improve crop yield. There are many methods to detect and estimate moisture content in plants. The image processing by using the projected area and color space of plant leaves in two-dimensional images is widely applied to detect water content. With the development of 3D point cloud technology, it has become an inevitable trend to use 3D information to study crop growth status. In this study, the monitoring models of strawberry leaf moisture content based on 3D geometric parameters were used to predict the leaf moisture content. The water content of 49 pots of strawberry “Ningyu” with different water treatments was measured. Geometric parameters of strawberry leaves were extracted by using real-time on-line 3D modeling to analyze the relations between water content and these parameters. Firstly, a binocular camera was set to capture the depth maps of strawberry leaves, which were converted into 3D point cloud images. Secondly, the strawberry leaves were segmented by using the 3D-SIS instance segmentation method. Thirdly, the random sampling consensus algorithm plus the global least-squares method was used to fit planes with the segmented 3D leaves to obtain the leaf inclination angle and corresponding cosine value. The blade spherical surface fitting method based on algebra was used to obtain the sphere radius to indicate the bending of leaves due to lack of water. Finally, the relation between water content and geometry parameters was analyzed quantitatively by using univariate and multivariate linear regression. In the univariate linear regression analysis, leaf inclination angle, cosine value, sphere radius, and leaf moisture content were linearly correlated, and the determination coefficients were 0.842 9, 0.854 6, and 0.880 8 respectively. In multiple linear regression analysis, the relation between water content and sphere radius plus leaf angle, and sphere radius plus cosine value was analyzed. The results showed that there was a significant correlation between the spherical radius, the leaf inclination angle, and the water content, and the modified coefficient of determination was 0.914 3. The prediction models were tested on the validation set and the results showed that among the above-said models, the one established by spherical radius and leaf inclination angle was best. The root mean square error was merely 0.015 8, and the determination coefficient was as high as 0.953 4. The proposed method could quickly detect the water content of strawberry leaves, providing an effective method for non-contact measurement of strawberry water content and technical support for the accurate acquisition of agricultural situation information. With the help of 3D geometric parameters of leaves, there was a prospect for the early application of plant water deficit control. The prediction model of leaf water content established by regression should have a certain application value in the field of ecology and crop protection.

fruit; models; image processing; strawberry; plane fitting; sphere fitting; leaf moisture content

符凯娟，冯全，杨森，等. 采用3D几何特征的草莓叶片含水率监测与试验验证[J]. 农业工程学报，2020，36(24)：161-169.doi：10.11975/j.issn.1002-6819.2020.24.019 http://www.tcsae.org

Fu Kaijuan, Feng Quan, Yang Sen, et al. Monitoring and experimental verification of strawberry leaf moisture content using 3D geometric features[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(24): 161-169. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.24.019 http://www.tcsae.org

2020-08-11

2020-09-29

甘肃农业大学学科建设专项基金项（GAU-XKJS-2018-188）；甘肃省高等学校产业支撑引导项目（2019C-11）

符凯娟，研究方向为图像处理、深度学习。Email：18809487363@163.com

冯全，博士，教授，博士生导师，研究方向为农业信息化、计算机视觉。Email：fquan@Sina.com

10.11975/j.issn.1002-6819.2020.24.019

S24

A

1002-6819(2020)-24-0161-09