某型导弹冷发射装备场坪适应性研究

张震东， 马大为， 仲健林， 高原， 王玺

(1.南京理工大学 机械工程学院, 江苏 南京 210094; 2.火箭军研究院, 北京 100089;3.北京航天发射技术研究所, 北京 100076)

0 引言

导弹发射装备在场坪上安全可靠地完成导弹发射任务，保证导弹出筒姿态的能力称为导弹发射装备对场坪的适应性。随着经济的快速发展，我国公路网络越来越密，为实现导弹的广地域发射奠定了坚实基础，但由于我国公路承载能力的多样以及发射场坪力学特性研究的不足，致使难以确定何种等级公路可安全可靠地进行导弹弹射。

目前国内外学者较注重导弹发射装备环境适应性研究[1-2]，只有少数文献视场坪(或路面)与发射装备作为一个系统进行分析。李涛等[3]利用谐波叠加法生成B级路面，建立了该型机枪刚柔耦合的路面- 车体- 机枪系统的虚拟仿真模型；综合考虑轮胎与地面、车体与机枪之间的相互作用，获得了各种车速条件下机枪射击时的枪口响应特性和弹着点散布情况。钟洲等[4]利用自回归(AR)模型对不同等级随机路面进行数值模拟，建立了车载防空导弹的行进和发射一体化多柔体动力学模型，分析了路面和车速对防空导弹行进间发射精度的影响。薛翠利等[5]以导弹箱式发射系统为研究对象，建立了导弹发射系统在其发射过程中4个阶段导弹的动力学模型，考虑了各发射角度、侧向场坪坡度等因素对导弹飞行性能的影响。程洪杰等[6-8]分析了导弹发射过程中的各种工况，并进行了力学计算，通过对比，判断出发射车对地最大载荷状态，并以此作为场坪强度评估的依据；同时，为评估发射场坪的强度稳定性，形成了发射场坪的极限承载力快速评估技术，在地基承载力计算模型的基础上，分析内聚力、内摩擦角以及上覆层厚度对极限承载力的敏感度，给出了发射场坪极限承载力随敏感参数变化的规律。吴邵庆等[9]分别利用能量法和有限元方法对运输车和弹体进行了动力学建模，建立了支撑处的自由度匹配车- 弹耦合振动模型，分析了路面激励下系统的振动量级，研究了不同弹体支撑刚度、车速和路面等级等因素对弹体某重要部位振动量级的影响，为导弹运输过程中振动问题提供了理论分析依据。冯勇等[10]在刚柔多体系统动力学的基础上，采用刚液耦合、刚弹耦合的方法，建立了某型多管火箭炮的发射动力学模型，较真实全面反映了整个火箭炮系统的力学特征。周晓和等[11]建立了某导弹无依托发射场坪塑性损伤动态本构模型，分析了导弹在待发射及发射状态下场坪的动态响应。孙船斌等[12]为研究冷发射平台垂直弹射响应特性，对车身进行柔性处理，建立了考虑场坪坡度的六自由度1/2冷发射平台弹射动力学模型和振动方程，研究了适配器刚度、液压支腿刚度及场坪坡度对冷发射平台弹射响应特性的影响。张震东等[13]为研究冷发射装备对地载荷作用下场坪的动力响应，将对地载荷视为多圆均布动载荷，基于赫兹接触理论获得对地载荷的表达式，给出了双参数地基模型上双层板的运动微分方程；在多体动力学仿真软件ADAMS中建立含场坪的发射装备动力学模型并与数学仿真软件MATLAB/Simulink进行联合求解，获得了各个接触区域圆心处的场坪下沉量。

综上所述，现有研究主要集中于车辆行驶过程中路面等级对武器射击精度的干扰分析、场坪倾斜程度对导弹出筒姿态的影响，但均没有建立起路面特征与射击精度、导弹出筒姿态间的量效关系，也没有给出哪些等级路面才可保证武器射击精度及发射品质。其主要原因在于：1)我国路面等级较多，且结构形式多样，研究对象很难覆盖所有场坪类型；2)路面特征与导弹(子弹)出筒姿态存在强非线性关系，难以用具体数学模型描述，很难建立显式的量效关系；3)研究过程需要进行大子样仿真，必须包含足够多的样本，工作量过大。

本文分析了场坪适应性的主要影响因素，利用场坪等效垂向刚度表征路面承载能力，并推导了场坪垂向刚度表达式，获取了导弹出筒过程风载计算式，利用试验设计方法和径向基神经网络算法建立了导弹出筒姿态近似模型，分析了其场坪适应性，为导弹发射装备的场坪适应性评估提供了一种借鉴方法。

1 场坪适应性影响因素与评价指标

1.1 冷发射装备组成及发射原理

图1为典型导弹冷发射系统的结构示意图，导弹发射平台主要由发射车、发射筒和导弹三部分组成。发射车部分主要包括驾驶室和仪器舱、发射车底盘、轮胎与油气悬架、液压起竖油缸、前后液压支腿等，发射筒部分主要包括发射筒、滑动式初容室、燃气发生器、适应性橡胶底座等，导弹部分主要有导弹弹体、适配器等。

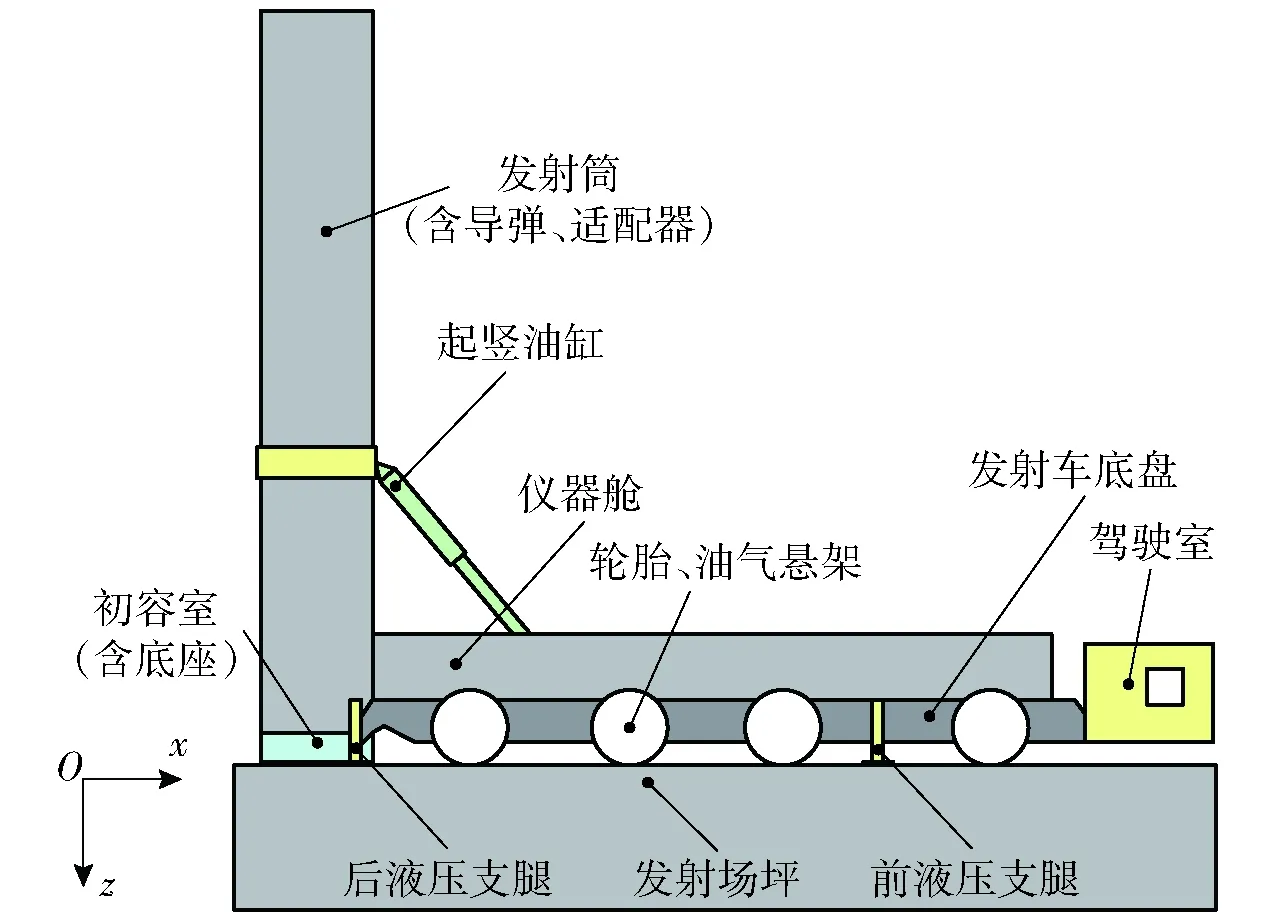
图1 冷发射系统构成Fig.1 Composition of cold launching system

导弹弹射时，燃气发生器在初容室内产生高压气体，作用于导弹尾罩，提供弹射动力，推动导弹出筒。同时，高压气体作用在适应性橡胶底座内壁面上，使其沿垂向和径向发生膨胀并和地面接触，以自动适应不同的场坪状态，并将大部分弹射载荷由接触界面传递至场坪表面，同时产生附加载荷以减弱由于弹重突然释放和发射筒壁动摩擦力引起的发射装置不稳定性。导弹运动过程中由自身摆动产生的动载以及发射装备自重，通过液压支腿传递至场坪表面。综上所述可知，导弹弹射过程中产生的载荷以及发射装备自重，均通过自适应底座、液压支腿等传递到发射场坪，故场坪的动态响应对发射过程的可靠性、导弹出筒姿态品质有重要影响。

1.2 场坪适应性主要影响因素与取值范围

由发射装备场坪适应性的内涵可知，场坪适应性受外界环境因素和装备自身性能两个方面的影响，装备定型后可认为其自身性能已经确定，本文只讨论外界环境因素对装备场坪适应性的影响。

1.2.1 主要影响因素

1.2.1.1 场坪承载能力及场坪坡度

由于场坪是发射装备的承载基础，发射过程产生的发射载荷以及发射装备自重都由场坪承受，因此场坪承载能力是重要影响因素之一，本文以场坪的垂向等效刚度反映场坪承载能力的强弱。

另外，弹射导弹前，发射装备必须经过车体的侧向调平、发射筒起竖过程，以减小车体及发射筒的侧倾角，但由于结构上的限制，发射装备的俯仰角不能进行调节，因此场坪的倾斜程度必将影响导弹的出筒姿态，本文采用场坪的纵坡角以及横坡角描述路面的倾斜情况。

1.2.1.2 装备与场坪间的摩擦系数

弹射载荷通过发射装备与场坪间接触界面传递至场坪，故发射装备对地载荷可由接触理论描述，法向接触力的大小主要影响装备的垂向响应，而接触界面间的摩擦力则会影响装备的横向响应，特别是场坪存在较大倾角时，摩擦系数对装备响应影响较大，因此场坪与装备间的摩擦系数是场坪适应性的影响因素之一。

1.2.1.3 风载荷

风也是影响场坪适应性的外界因素，风载荷大小可由风速及装备结构特性确定。考虑到发射装备结构的周向非对称性，不同的风向，装备响应并不相同。因此，在结构特性一定的情况下，对于风载荷本文采用风速和风向两个参数描述。

综上所述，发射装备场坪适应性的主要影响因素包括：场坪垂向等效刚度、场坪横坡角、场坪纵坡角、装备与场坪间的摩擦系数、风速及风向。

1.2.2 场坪垂向等效刚度的确定

本文采用适用于较大变形的多层弹性体系理论，确定场坪垂向刚度。

1.2.2.1 多层弹性体系的传递关系

直角坐标系下求解多层弹性体的轴对称问题，假设x轴、y轴方向场坪尺寸足够大，如图2所示。图2中：r为载荷作用面半径；hn为各层厚度；En为各层弹性模量；μn为各层泊松比；F(x,y,t)为作用载荷；N为总层数；n=1，2，3，…，N.

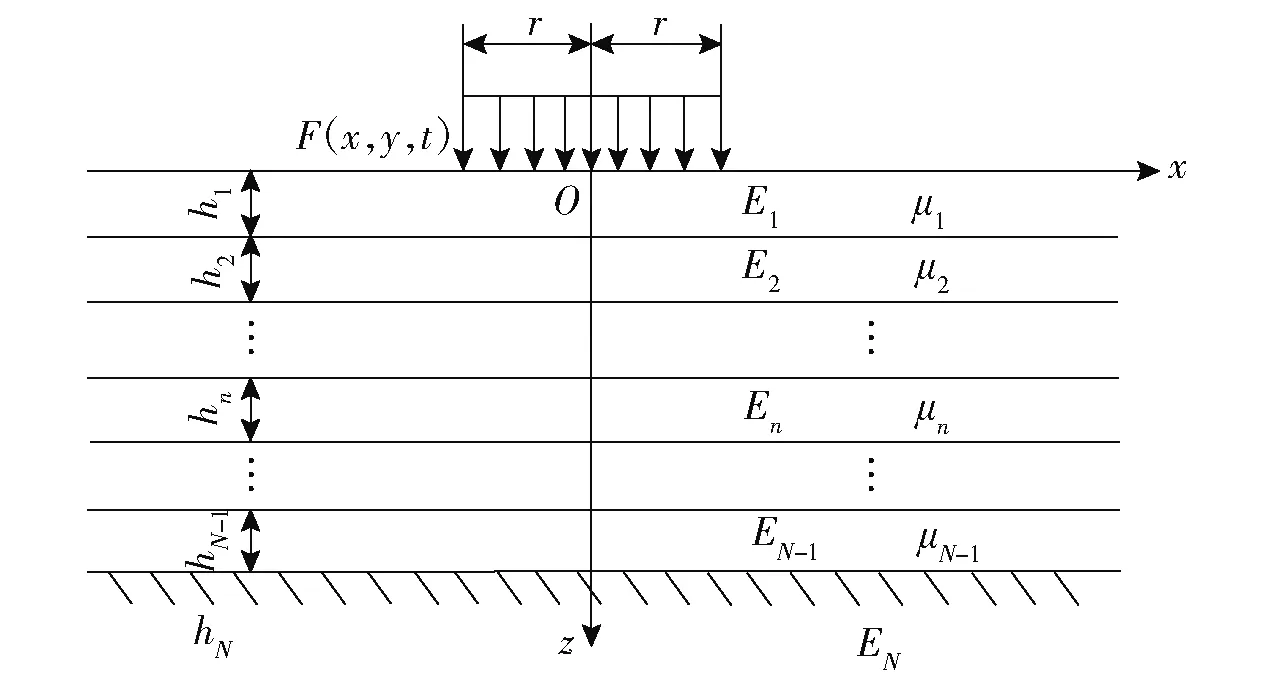
图2 多层弹性体系Fig.2 Muti-layered elastic system

利用传递矩阵方法，推导出多层弹性半空间轴对称问题、层间完全接触情况的路面等效刚度解析解，具体求解过程如下：

1)弹性问题的基本方程。不计体力时，直角坐标系下对弹性问题的平衡方程、几何方程及物理方程，分别为

σij,j=0，

(1)

(2)

σij=λεkkδij+2μεij，

(3)

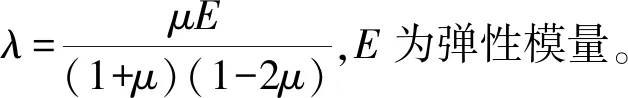
2)单层体系的传递关系。为方便公式推导，本文定义如下变量：

(4)

式中：ux、uy、uz分别为x轴、y轴、z轴方向的位移；σz为z轴方向的正应力；τxz、τyz分别为Oxz平面、Oyz平面的切应力。

综合(1)式～(4)式，可得

(5)

定义二维Fourier变换对为

(6)

式中：ξ、ζ为复变量。

对(5)式进行二维Fourier变换，得

(7)

(7)式写成矩阵形式，即

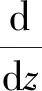
(8)

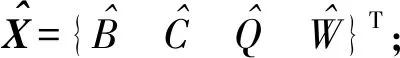
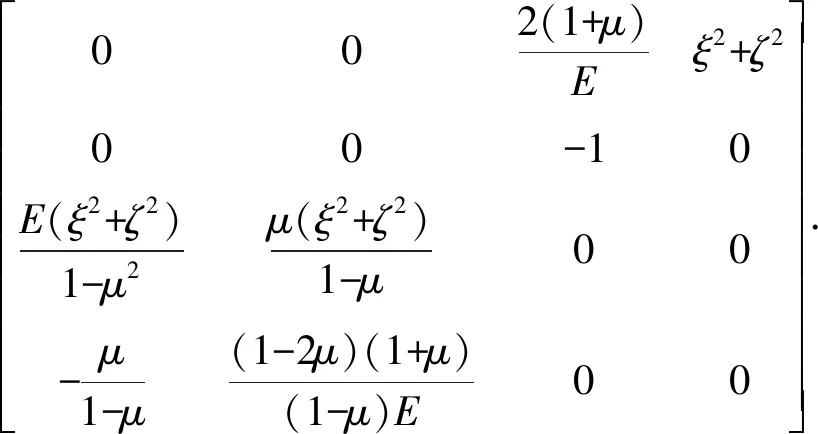
1.2.2.2 传递矩阵求解方法

(8)式解的形式[14]为

z=eAnz0，

(9)

Tn=eAnz=L-1{[qI-An]-1}，

(10)

q为对z进行Laplace变换后的复变量。由(10)式可求得场坪各层的传递矩阵Tn.

假设层间状态完全连续，通过逐层传递，可得到多层弹性体系的传递关系[14]为

(11)

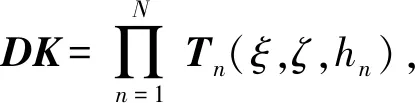
(12)

1.2.2.3 场坪垂向刚度求解

本文假设发射载荷通过圆形承载面传递至场坪，则场坪表面的圆形均布载荷可表示为

F(x,y,t)=f(t)×H[r2-(x2+y2)],

(13)

式中:f(t)为载荷平均集度；H(x,y)为Heaviside阶跃函数。

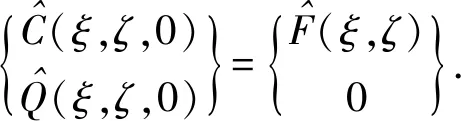
由边界条件以及(12)式，可得

(14)

由(14)式二维Fourier变换后的场坪垂向位移为

(15)

由(15)式二维Fourier变换后的场坪垂向刚度为

(16)

对(16)式进行二维Fourier逆变换就可求出场坪的垂向刚度。

为保证场坪垂向刚度取值范围的覆盖性，选取了2种高速公路、4种等级沥青混凝土路面进行垂向刚度计算，路面结构见表1，计算结果如表2所示，根据计算结果取场坪等效垂向刚度取值范围为2.0×104～2.0×105N/mm.

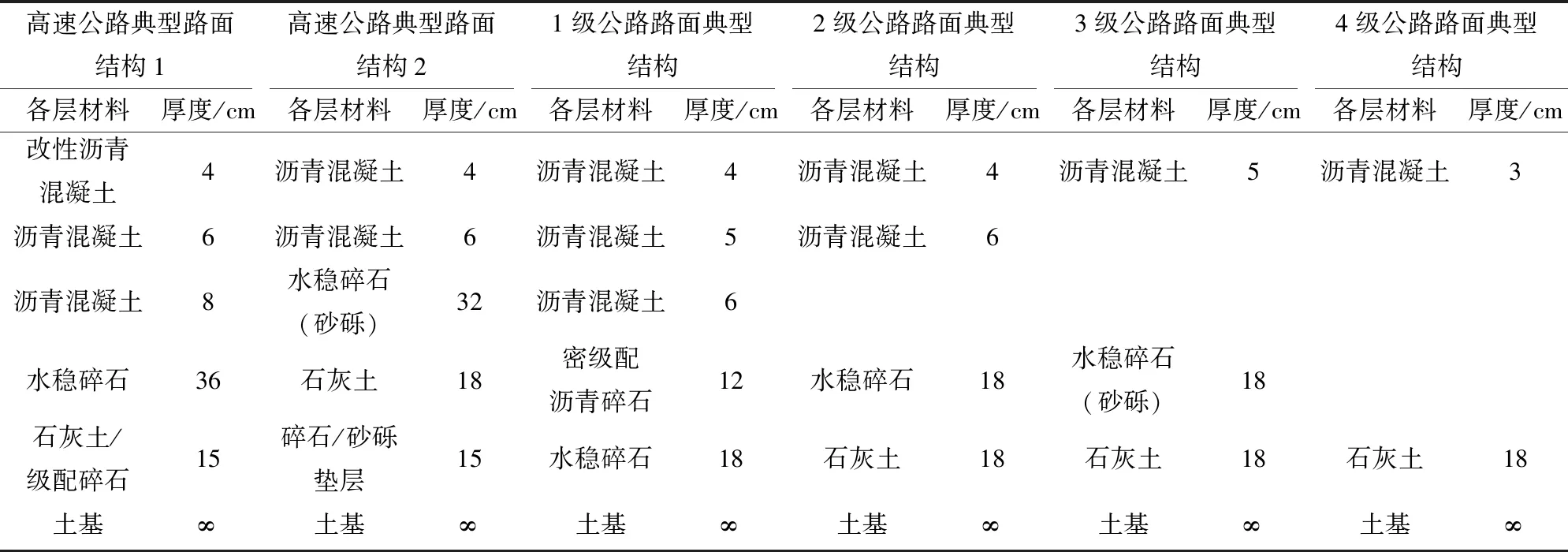
表1 沥青混凝土路面典型结构Tab.1 Typical structures of asphalt pavement

表2 典型路面等效刚度Tab.2 Equivalent stiffness of typical pavement

1.2.3 导弹出筒过程中的风载荷

文献[15]分析了悬垂状态时，风载荷作用下装备的响应，本文在此基础上研究风载荷对导弹出筒过程的影响。由于导弹出筒时间很短，在短时刻内可将风速视为常值。风载荷在导弹上的作用面随导弹出筒过程不断改变，即载荷作用面和高度均为时间的函数，如图3所示。图3中：∑Fm为风载荷；Hc(t)为导弹出筒距离，即出筒过程中导弹的行程；Hm为导弹总长；H为发射筒总长；∑Mm为等效力矩。

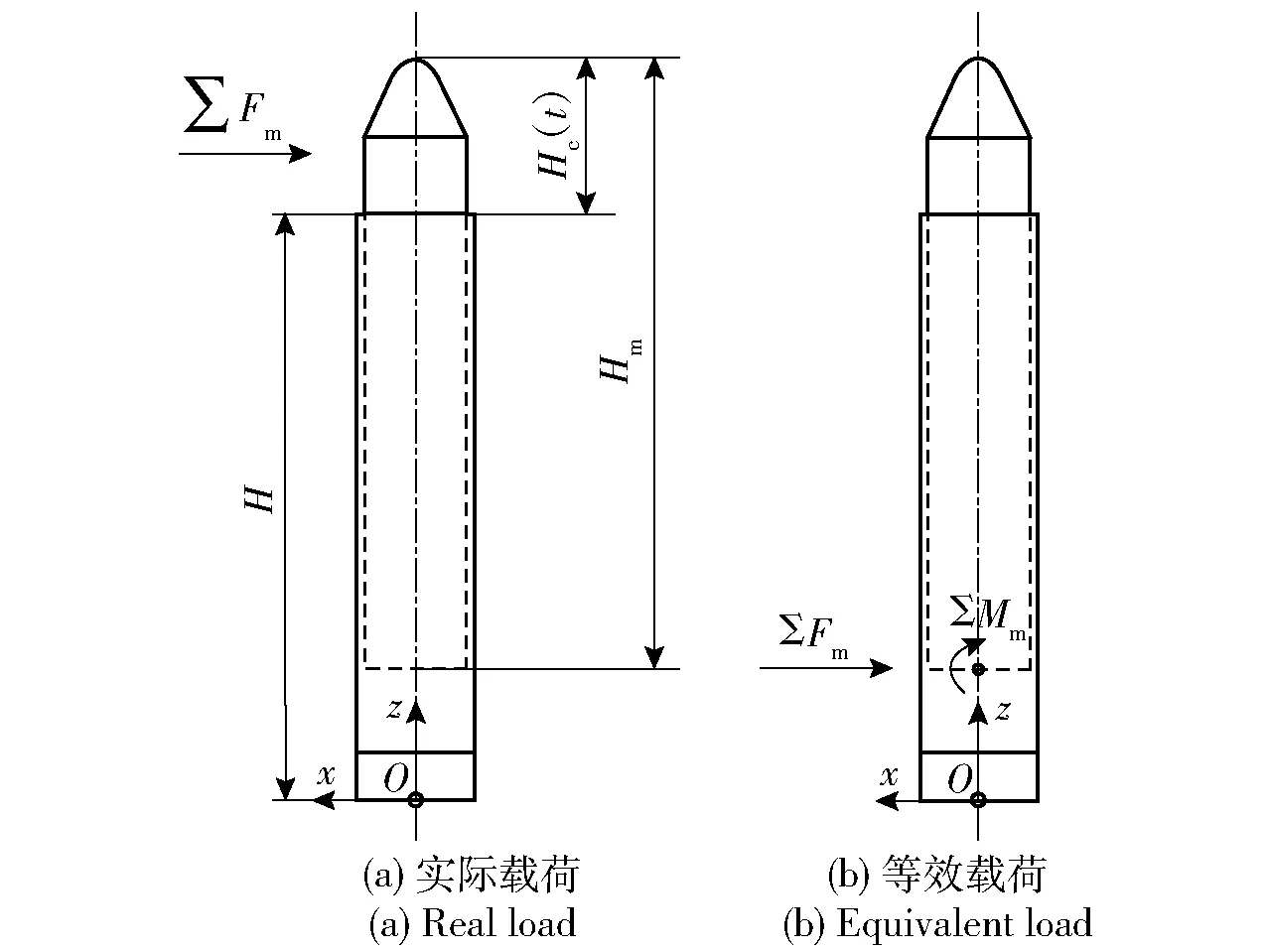
图3 导弹出筒过程示意图Fig.3 Schematic diagram of missile launching

由于导弹前端头部圆锥部分较短，故将导弹视为圆柱体，文献[15]中风载荷计算公式可改为

(17)

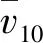
将风载荷移至导弹底部后，需增加的等效力矩为

[z+Hm-H-Hc(t)]dz.

(18)

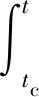
利用发射装备有限元模型进行动力学分析，获得导弹前端出筒时刻tc为0.4 s左右，给出了平均风速为10 m/s时，导弹出筒过程中所受等效风载荷、等效风力矩如图4和图5所示。

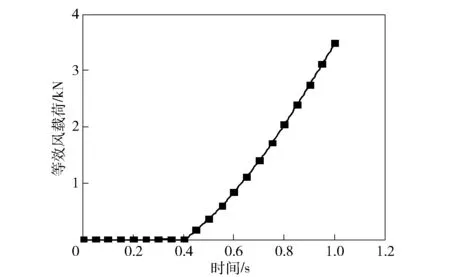
图4 导弹出筒过程中的等效风载荷Fig.4 Equivalent wind load during launching

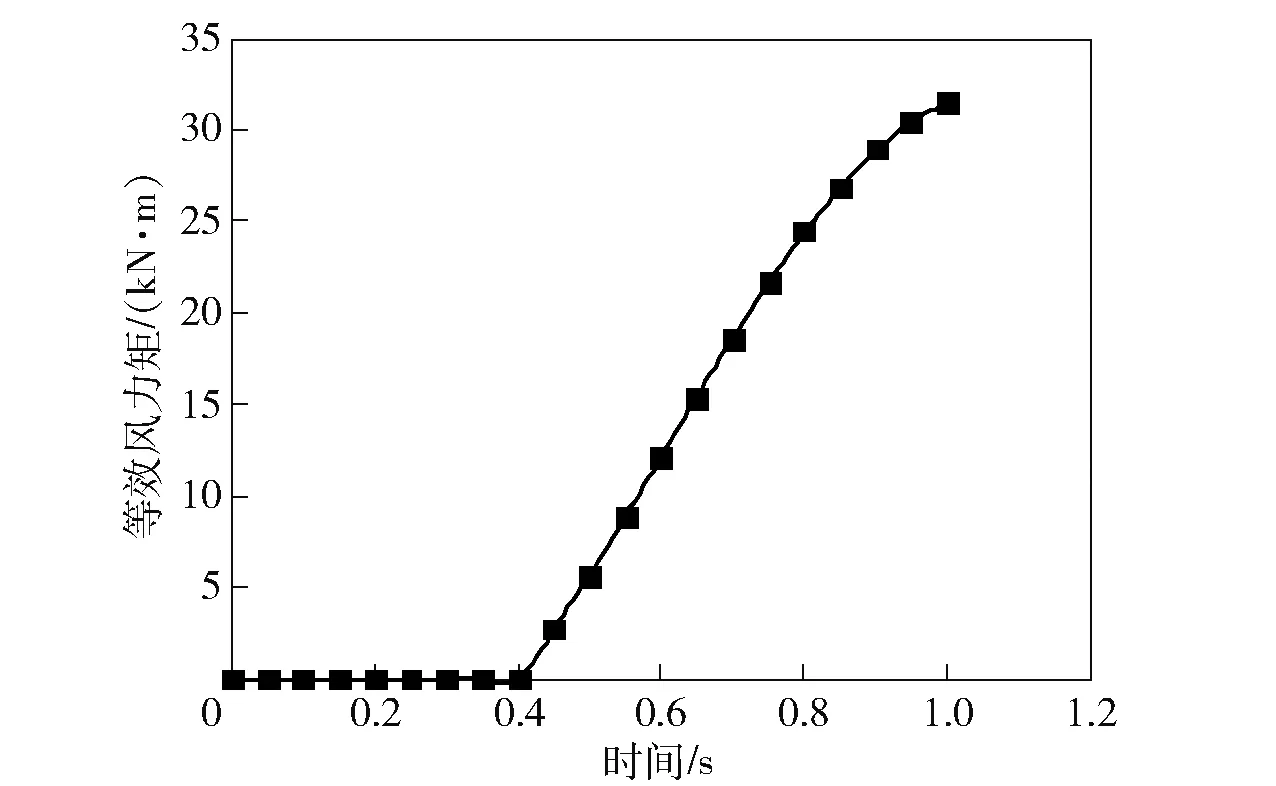
图5 导弹出筒过程中的等效风力矩Fig.5 Equivalent wind moment during launching

1.2.4 影响因素取值范围

根据发射装备相关部件性能指标、公路路线设计规范JTG D20—2017等，具体影响因素可能的取值范围，如表3所示，表中：Kls为场坪等效刚度；Sl为场坪纵坡角；Sc为场坪横坡角；fc为橡胶与路面摩擦系数；vw为风速；Sw为风向。

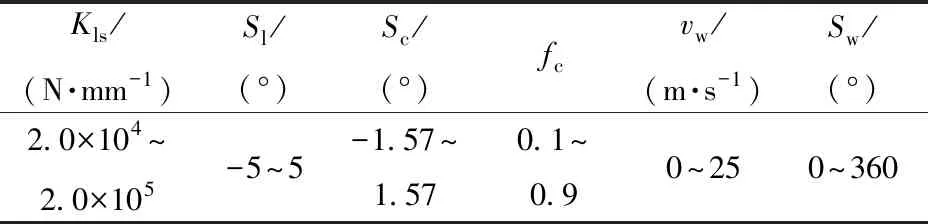
表3 场坪适应性主要影响因素及其取值范围Tab.3 Main influencing factors of adaptability to launching site and its range

1.3 场坪适应性评价指标

根据发射装备场坪适应性的内涵，需通过导弹的出筒姿态来评价此发射装备在某种场坪上能否进行导弹弹射，工程上一般采用导弹绕质心的角位移、角速度、角加速度进行表征。对于冷发射装备而言，由于出筒过程中适配器的导向和缓冲作用，导弹出筒时的角加速度较小，一般均能满足导弹出筒姿态要求，因此以导弹出筒时的姿态角及姿态角速度作为发射装备场坪适应性的评价指标，具体包括俯仰角及其角速度、偏航角及偏航角速度。根据该型导弹性能指标要求，在导弹出筒后，为使姿控发动机安全准确的对导弹姿态控制和调整，需满足导弹的出筒姿态角和姿态角速度绝对值分别不超过5°和5°/s.

2 导弹出筒姿态近似模型

研究发射装备的场坪适应性，需要大量仿真计算工作，以涵盖足够多的影响因素样本，若仅采用有限元模型或者多体动力学模型进行计算，仿真周期较长，而且目标函数和变量之间的强非线性关系，以及变量之间的相关性，难以用显示数学模型准确描述，因此常规数学方法难以建立导弹出筒姿态与影响因素间的精确量效关系，故本文采用拉丁超立方试验设计方法和径向基神经网络结合的方法，在保证量效关系精度的同时，尽可能地减小计算样本数量。

2.1 样本空间获取

拉丁超立方设计[16]是目前最有效的试验设计方法之一，它采用等概率随机正交分布的原则，可以在极少的试验点数情况下得到较高精度的近似函数。

综合考虑6个场坪适应性变量设计空间的大小和近似函数的形式，优化拉丁超立方构建的6个影响因子共30组数据样本空间如表4所示。

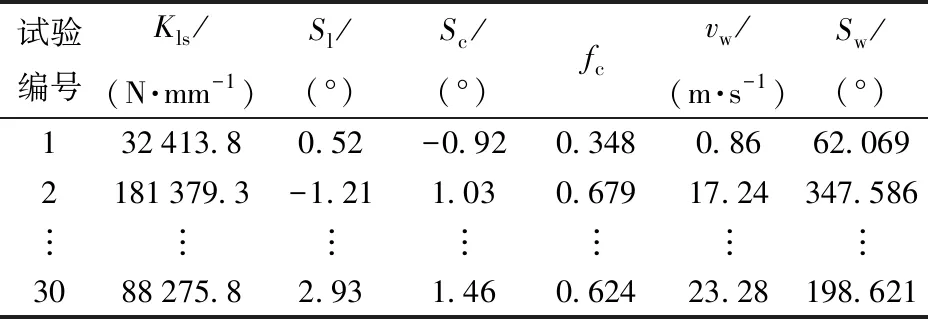
表4 场坪适应性影响因子样本空间表Tab.4 Sample space table for influencing factor

2.2 近似模型构建

径向基神经网络是基于人脑的神经元细胞对外界反应的局部性而提出的，是一种新颖有效的前馈式神经网络，由于其结构简单、训练简洁而且学习收敛速度快，具有较强的非线性映射能力，能以任意精度全局逼近一个非线性函数，在很多领域得到了广泛应用[17]。

径向基神经网络的结构可得到网络的输出为

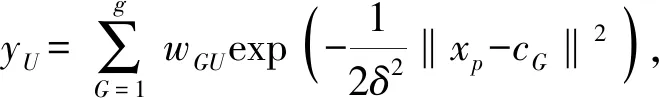
(19)

式中：xp为第p个输入样本，p=1，2，3，…，P，P为样本总数；cG为网络隐含层的节点中心；wGU为隐含层到输出层的连接权值；G=1，2，3，…，g为隐含层节点数；yU为与输入样本对应的网络第U个输出节点的时间输出；m为节点总数；δ为基函数的方差。

设dU是样本的期望输出值，那么基函数的方差可表示为

(20)

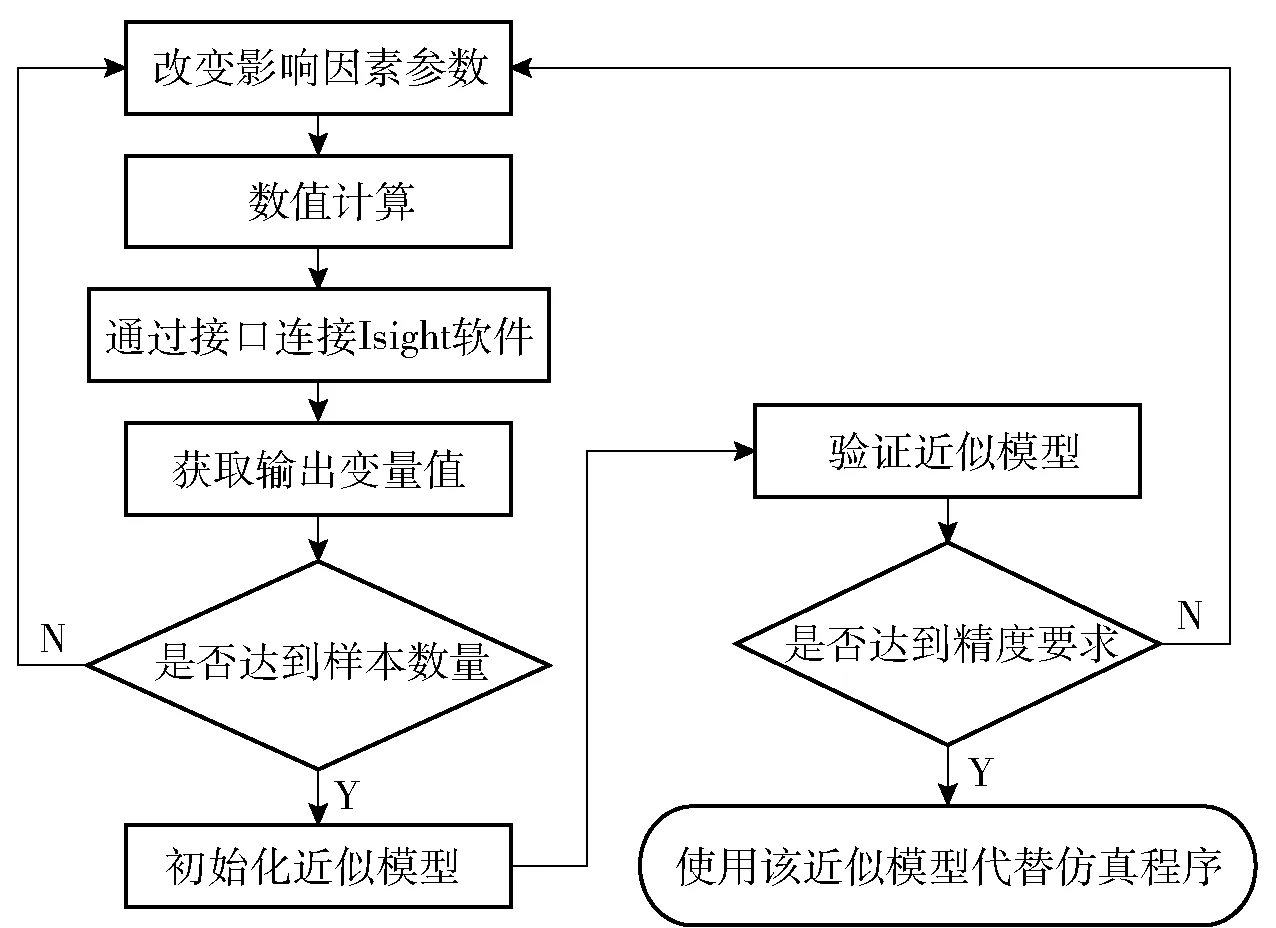
图6 近似模型建立流程Fig.6 Establishment process of approximate model

本文采用径向基神经网络法建立导弹出筒姿态的近似模型，建立流程如图6所示。

2.3 近似模型有效性验证

2.3.1 评价指标

以场坪适应性影响因素样本空间为输入条件，基于含场坪的导弹冷发射装备有限元数值模型，进行发射动力学分析，得到导弹出筒时的姿态角位移和姿态角速度，如表5所示，表中φx、φy、ωx、ωy分别为导弹出筒后的x轴、y轴方向姿态角和姿态角速度。

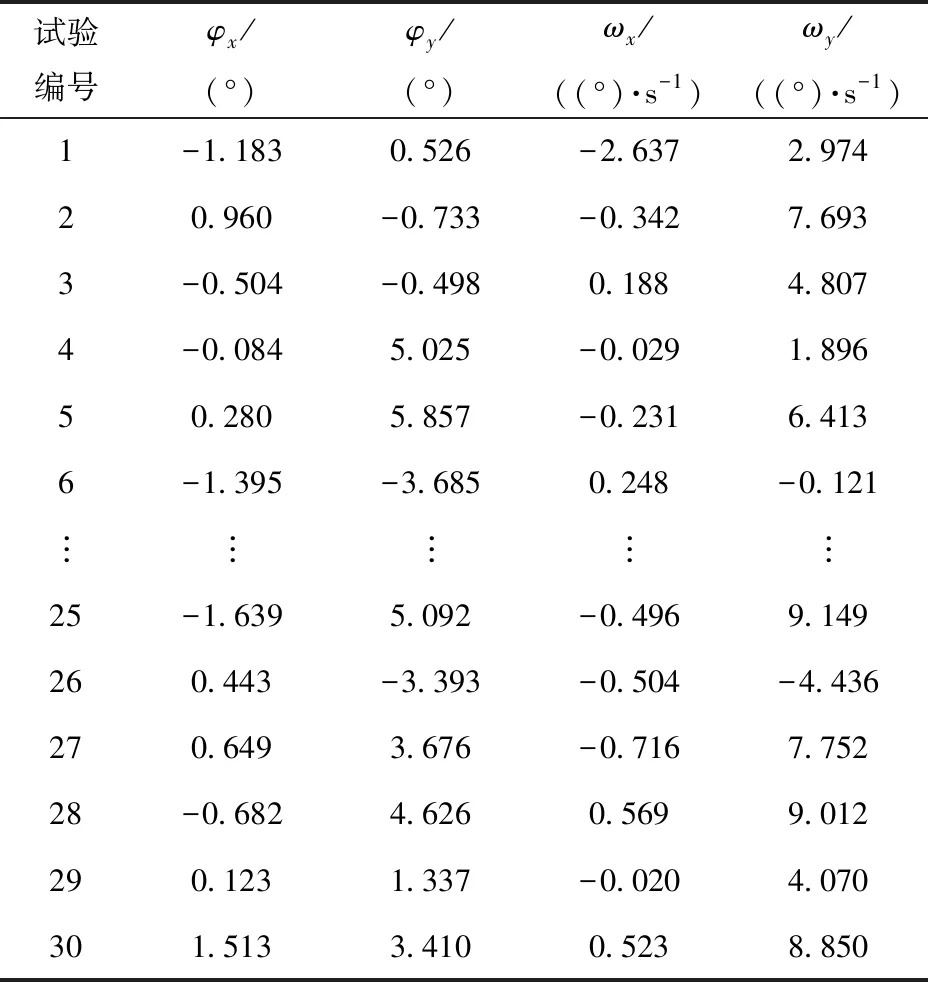
表5 导弹出筒姿态角位移及角速度Tab.5 Attitude angle and angular velocity of missile

2.3.2 误差分析

利用径向基神经网络对上述拉丁超立方试验设计方法的试验数据进行训练，得到近似模型网络结构，从训练样本中随机选取5组数据对近似模型进行误差分析，分析结果如表6所示。

由表6可知，随机选取的5组数据中，采用径向基神经网络训练得到的近似模型计算结果与有限元仿真结果最大相对误差为13%，精度较高，在后续研究中，可以采用此近似模型来代替有限元模型。

2.3.3 方差分析

方差分析认为响应的总方差来源于两部分的贡献，分别为近似模型本身，以及拟合误差。方差分析需要采用离均差平方和，定义[18]为

(21)

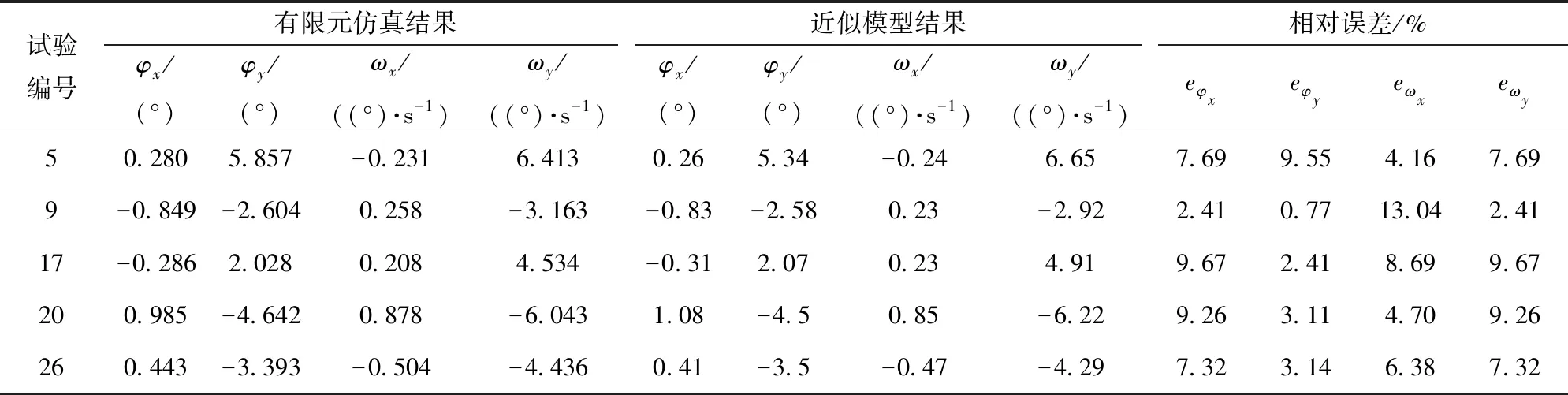
表6 近似模型误差分析Tab.6 Error analysis of approximate model

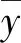
采用R2来描述前文中的径向基神经网络近似模型的拟合精确度，R2越接近1表明拟合得越精确，R2定义为R2=SSM/SST. 如图7所示，对于导弹的φx、φy、ωx、ωy的R2方差均较接近于1，近似模型较为准确。

图7 φx、φy、ωx、ωy的方差分析Fig.7 Variances of attitude angle and angular velocity

2.4 导弹出筒姿态敏感度分析

采用多元二次回归方法，在径向基神经网络近似模型学习训练的基础上，对导弹出筒姿态的影响因素进行敏感度分析。

多元二次回归模型[18]为

(22)

式中：b0、bq、cq、θqs为回归系数；xq、xs为自变量。

以两个输入变量模型为例，其多项式构成为

(23)

其导数为dy=b1dx1+b2dx2+2b3x1dx1+2b4x2dx2+b5dx1x2.

x1、x2线性项的主效应分别为b1dx1、b2dx2，2阶项主效应分别为2b3x1dx1、2b4x2dx2，交互效应为b5dx1x2.

计算得到导弹出筒后，其角位移，角速度对影响因子的敏感度如图8所示，图中以横坐标0点处的纵坐标轴为界限，下方条形表示负效应，上方条形表示正效应。

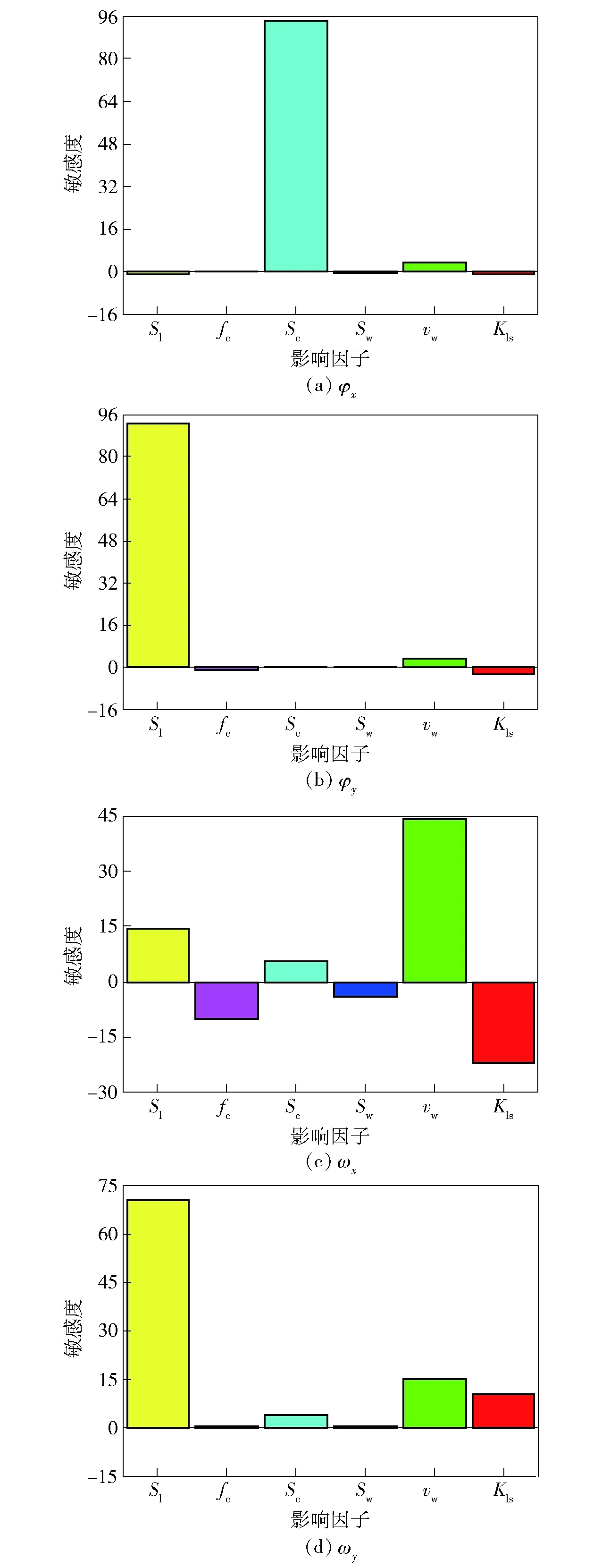
图8 场坪适应性影响因素的敏感性Fig.8 Sensitivity on adaptability of factors

由图8(a)可以看出，导弹出筒后x轴方向角位移φx对影响因子的敏感性高低顺序为：横坡角Sc、vw风速、场坪等效刚度Kls、纵坡角Sl、风向Sw、摩擦系数fc. 同样可通过图8(b)、图8(c)、图8(d)对影响因子进行分析。

在场坪适应性分析时，选用对导弹角位移敏感性最高的影响因素和对角速度敏感性最高的影响因素为分析变量，以判定导弹场坪的适应性。

综合上述分析，装备场坪适应性影响因素敏感度较强的因子包括：场坪等效刚度、场坪纵坡角、风速、场坪横坡角。

3 场坪适应性综合判据

影响发射装备场坪适应性的因素很多，仅仅基于其他因素取基准值对单个因素的边界条件分析是远远不够的，因为由于发射过程的不确定性等原因，需要在其他影响因素取某一值的情况下，对某因素进行边界条件分析。对于建立场坪适应性多因素综合判据中最困难的是对多因素的表达，本文采用三维空间的方式把单因素作为维度，通过曲面的方式来展示场坪适应性的综合判据。

根据因素的敏感性抽取关键因素，用函数表达建立综合判据方程，假设适应性综合判据由3个关键因素变量所确定，其空间就是三维的。如果场坪适应性的影响因素在三维空间的区域以内表明导弹出筒姿态处于可控态，在空间以外处于非可控状态。选择3个主要的组合参数，场坪纵坡角、场坪等效刚度、风速作为变量，形成三维空间区域，画出三维曲面，形成场坪适应性综合判据，如图9所示。图9中下曲面以上以及上曲面以下的3个参数取值均可保证导弹出筒姿态，其他的所有组合取值不满足导弹出筒要求。

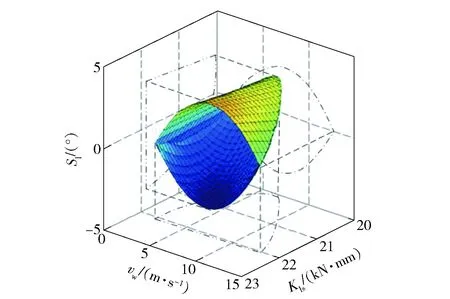
图9 场坪适应性综合判据Fig.9 Synthetic criterion of adaptability

从图9中可以看出，对于本文研究的导弹发射装备而言，在较小的场坪纵坡角和风速条件下，较低承载能力的路面就可以保证导弹出筒姿态。从三维空间曲面的包络边界可知，在路面纵坡角小、风速低的情况下，低承载能力路面就可作为导弹的发射场坪，说明该型装备的场坪适应性较强。对于承载能力高的场坪，即使发射装备在大的纵坡角和风速条件下进行导弹弹射，也可保证导弹出筒姿态处于可控范围，确保发射品质。对于本型装备要求导弹的出筒姿态角和姿态角速度绝对值分别不超过5°和5°/s，当风速不大于2.5 m/s，路面纵坡不大于1.2°，等效刚度为2.00×104N/mm的路面时仍能保证导弹出筒姿态，因此路面结构形式6(4级沥青路面，等效刚度为3.12×104N/mm，如图10所示)也可保证导弹发射要求。

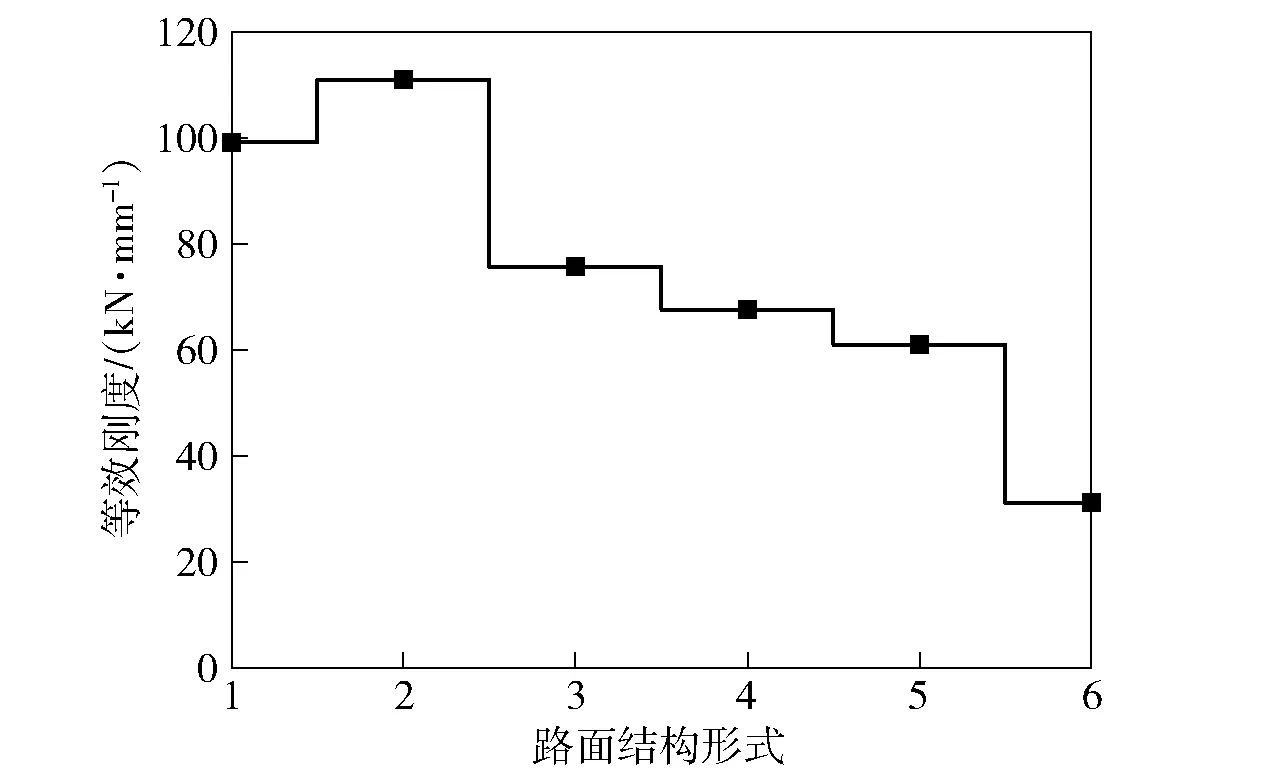
图10 典型路面等效刚度Fig.10 Equivalent stiffness of typical pavement

4 结论

本文通过分析，确定了场坪适应性的影响因素和评价指标，基于多层弹性理论体系推导了场坪等效垂向刚度解析公式，建立了导弹出筒过程中风载荷的计算方法。在大子样仿真数据的基础上，利用径向基神经网络法构建了导弹出筒姿态近似模型，并分析了各影响因素对场坪适应性的敏感度。在此基础上分析了某型导弹冷发射装备的场坪适应性。通过分析可得以下主要结论：

1)该型装备的场坪适应性影响因素敏感度较强的因子包括：场坪等效刚度、场坪纵坡角、风速、场坪横坡角。

2)该型装备在风速较小情况下，低等级路面上就可安全发射，承载能力高的路面上，较大纵坡角、较高风速的情况下也可保证导弹出筒姿态。当风速不大于2.5 m/s，路面纵坡角不大于1.2°时，4级沥青路面即可满足该型导弹发射要求。