综合优先级下反导预警相控阵雷达任务调度算法

杨善超， 田康生， 李宏权， 周广涛， 梁复台

(1.空军预警学院 预警情报系, 湖北 武汉 430019; 2.31101部队, 江苏 南京 210016)

0 引言

相控阵雷达可以实现波束自适应捷变，拥有丰富的工作波形和强大的资源配置，相比机械扫瞄雷达优势巨大，是执行反导预警任务的主要装备[1-2]。为提升相控阵雷达时间资源利用效率，发挥相控阵雷达性能优势，更好执行反导预警任务，必须要进行时间资源分配，也就是任务调度[3-4]。

相控阵雷达任务调度器主要包含两个模块：任务优先级规划和调度策略选取。简单的优先级规划，是单因素确定任务优先级，包括高任务模式优先级最优先(HPF)算法[5]和截止期最早最优先(EDF)算法[3-4,6]。仅利用一种参数确定优先级，分析不够全面，进而影响优先级的动态自适应性。文献[7-10]借鉴优先级表思想[11]，结合工作方式优先级和截止期进行综合优先级规划，提出工作方式优先级加截止期(HPEDF)算法及其两种变形算法：修正EDF(MEDF)算法和修正HPF(MHPF)算法，并仿真验证了这3种综合优先级算法的性能优势。然而上述算法在规划优先级过程中没有充分利用目标先验信息，且存在人为划定工作方式优先级而导致主观性过强的问题。针对此问题，文献[12-14]建立关于目标属性的威胁度模型，通过目标威胁度和任务截止期共同确定任务优先级。雷达调度策略主要包含模板类策略和自适应策略两类，后者更能发挥相控阵雷达性能优势。文献[15-17]利用时间窗方法进行动态任务调度，使雷达任务请求的实际执行时刻可以在其期望时间前后移动，极大提高了调度成功率和时间利用率。文献[14,18-21]采用了任务交错算法，使任务等待期可以发射或接收其他任务驻留的波束，进一步提高了时间利用率。文献[22,25]提出了基于代价或收益的调度算法，构建任务调度优化模型，并利用二次规划、启发式算法等进行求解。此外，文献[26-27]提出了动态驻留时间调度算法，将任务驻留时间设定为模糊集，增强了任务调度的灵活性。总的来看，上述研究不适用于多弹道导弹目标跟踪任务的调度，主要由于：1)任务优先级规划大多针对空中目标，不符合弹道导弹目标特性；2)弹道导弹跟踪任务对于及时性要求很高，而上述调度策略没有充分考虑调度及时性。此外还存在将任务价值作为一个固定参数，没有考虑其随执行时刻动态变化的问题。

因此，本文提出综合优先级下基于价值优化的反导预警相控阵雷达调度算法。该算法中优先级规划符合弹道导弹目标特性，且调度策略使任务请求贴近期望时刻被执行，更满足调度及时性原则。

1 弹道导弹目标威胁度模型

弹道导弹飞行速度快、机动性强、破坏杀伤性大，对防御方存在巨大威胁；另一方面，其飞行弹道和目的点是可预测的。因此分析弹道导弹目标威胁度过程中，不仅要考察导弹自身属性因素，还要考察导弹和目的地之间的相互关系，以及目的地的重要程度，影响因素主要考虑以下5方面：目标速度、目标飞行阶段、目标距目的地距离、目的地重要程度、弹头种类。考虑到各影响因素对目标威胁度的非线性影响，分别对其构建如下威胁度函数：

1) 目标速度威胁度：

(1)

式中：v为目标速度；vc为临界速度；a为控制速度威胁函数的常系数，一般取[0.01,0.10]，a越大，曲线上升拐点处的v越大，且之后曲线上升越快。该函数表明随着目标速度变大，威胁度不断增大，当速度大于临界值时，威胁度一直处于最大状态。

2) 目标飞行阶段威胁度。弹道导弹飞行过程可以分为3部分：主动段、自由飞行段、再入段。处于主动段时，目标速度相对较慢，防御方反导系统应对时间相对较长，威胁度最小。自由飞行段在飞行过程中占比最大，此阶段防御方仍有一定应对时间，但是目标逐渐飞临目的地，威胁度增大。处于再入段时，目标速度急剧增大，已经非常迫近攻击目标，留给防御方的反应时间很短，威胁度最大。因此建立如下飞行阶段威胁度函数：

(2)

式中：下标s表示目标所处的飞行阶段；Wsr、Wsf、Wsp分别为3个目标飞行阶段对应的威胁度设定值。

3) 目标距目的地距离威胁度。目标离目的地越近，距其造成杀伤的时间越短，威胁度越大。例如同样处于主动段的2个目标，一个自3 000 km之外发射，一个自1 000 km之外发射，攻击同一个目的地，显然后者威胁度更大。建立距离威胁度函数为

Wr=(1-b)exp(-cr)+b,

(3)

式中：r为目标离目的地距离(km)；b为最小距离威胁度；c为控制目标距离威胁度函数的常系数，c越大，曲线拐点处的目标距离越小，曲线越接近呈现“L”形分布。

4) 目的地重要程度威胁度。弹道导弹目标的攻击目的地可预测，目的地属性是决定目标威胁度的重要因素。根据作战层次分级，将目的地重要程度分为战略、战役、战术3类，对应建立威胁度函数为

(4)

式中：下标d表示目的地重要程度，具体分级由专家确定；Wds、Wdc、Wdt分别为3个不同目的地重要程度对应的威胁度设定值。

5) 弹头种类威胁度。弹头是弹道导弹的战斗部，部分导弹具备载核能力，将弹头分成核弹头、常规弹头两类，构建如下威胁度函数：

(5)

式中：下标h表示目标携带弹头种类；Whn、Whc分别为2个弹头种类对应的威胁度设定值。

基于以上各影响因素的威胁度函数，构建弹道导弹目标威胁度模型：

W=δ1Wv+δ2Ws+δ3Wr+δ4Wd+δ5Wh，

(6)

2 任务综合优先级规划

任务调度一般以调度间隔S为周期，在调度间隔[t0,t0+S]内共有N个任务驻留请求，第i个任务请求可以表示为

Ti={pi,tai,tdi,tei,tdwi,Δti,Ii},

(7)

式中：pi表示任务工作方式；tai为请求到达时刻，tdi为截止期，因此任务时间窗为[tai,tdi]；tei为期望执行时刻；tdwi为驻留时间；Δti为采样间隔；Ii为目标信息集合，Ii可进一步描述为

Ii={v,s,r,d,h,W}.

(8)

(8)式中变量均满足(6)式，需要注意的是：当pi为搜索任务时，Ti中不包含目标信息集合。

从任务调度的重要性和紧急性原则[10]出发，利用优先级表思想[11]，结合弹道导弹目标威胁度和任务截止期进行综合优先级规划。将任务集合中所有任务按照目标威胁度由大到小排列，得到威胁度序列{W1,W2,…,WN}，其中搜索任务在序列中排在所有跟踪任务之后，搜索任务之间按照请求到达时间tai由前到后排列。再将所有任务按照截止期由小到大排列，得到截止期序列{d1,d2,…,dN}。将任务Ti在两个序列中的位置序号分别记为m、n，加权综合的优先级计算公式[12]为

Pi=[α·(m-1-β)+2·n-2]·(m+β)+m,

(9)

式中：α表示侧重目标威胁度的加权系数；β=⎣(m-2)/α」.Pi越小，对应任务的优先级越高。α取值一般在[1,4]，值越大，综合优先级越倾向于目标威胁度，当目标威胁度大小一致时，截止期越小的任务综合优先级越高。图1为α=1、α=2两种情形下的优先级表设计。

图1 优先级表设计Fig.1 Design of priority table

通过该动态优先级表设计，不用对目标威胁度和截止期进行去量纲处理，每个任务对应唯一的综合优先级，且增强了优先级表的动态自适应特性。

3 基于价值优化的调度策略

3.1 任务价值模型

实际上，任务执行时刻变化时，会导致目标跟踪精度和搜索发现概率的不同，必然会对任务实现价值产生影响。因此，任务实现价值不应该是固定值，而是随着执行时刻动态变化的。构建如下任务动态价值函数：

(10)

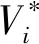
(11)

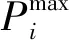
任务Ti的价值变化斜率包括两部分，分别对应着相对期望时刻提前或滞后执行，本文将二者的价值变化斜率绝对值大小设为一致，建立价值变化斜率函数为

(12)

式中：ξ为控制价值变化斜率的常系数。当ξ∈(0,1]时，不同优先级任务之间的价值变化斜率差异呈现增大趋势；当ξ>1时，价值变化斜率差异呈减小趋势；特别地，当ξ→∞时，所有任务的价值变化斜率都趋向于0. 可以看出，优先级越高的任务，价值变化斜率绝对值越大，任务动态价值随执行时刻变化下降越快。

3.2 价值优化调度模型

本文综合优先级规划过程体现了任务调度的重要性、紧急性原则。弹道导弹目标具有高机动性、高威胁性，对于任务调度及时性的要求非常高，要从及时性原则出发构建调度模型。(10)式反映出任务调度及时性越高，实现价值越大，因此构建价值优化调度模型为

(13)

(14)

式中：C1表示被调度任务执行时刻的前后关系以及总驻留时间约束；C2、C3分别表示被延迟、删除任务的时间约束；ηi表示任务调度属性，取值规则为

(15)

f(ηi)是关于任务调度属性的函数，

(16)

综上可以看出，优化调度等价于在满足(14)式的约束下，使(13)式所表示的总实现价值最大，主要目的包括两个：一是判断任务调度属性；二是对被调度任务选择优化执行时刻。

3.3 调度模型求解算法

上述优化调度问题可以视为一个高维的线性规划问题，运用传统的单纯形法或者遍历算法求解此类问题，会产生较大的计算量。遗传算法(GA)[28]是一种模仿生物遗传机制的智能搜索算法，能够有效减少求解调度模型的计算量。但是传统的GA搜索效率不高且容易陷入局部最优，因此本文设计一种改进的GA(MGA)，算法中选择操作采用精英保留和排名选择相结合的策略，并设置自适应的交叉、变异算子，以增大种群多样性、避免陷入局部最优、提高算法效率。

3.3.1 种群初始化及适应度计算

随机产生规模为Z的初始种群，每个染色体表示一种任务调度方案，由N个代表雷达任务的基因组成。基因采用两位二进制编码方案，“11”表示该基因对应的任务被执行，“10”或“01”表示任务被延迟，“00”表示任务被删除。

将个体对应的总实现价值Vtot作为其适应度，调度模型的目标函数为适应度函数。

3.3.2 选择算子

采用精英保留和排序选择相结合的策略：将个体按照适应度由大到小排列，保留种群中适应度最大的个体不参与交叉、变异操作，而是用其替换子代中适应度最低的个体；此外，其他Z-1个个体根据适应度采用轮盘赌法确定父本。轮盘赌法选择的公式为

(17)

式中：PRSk为个体k被选择的概率。

3.3.3 交叉算子

从群体进化过程来看，随着进化的推进，交叉概率呈现出减小趋势，以避免在算法后期因交叉概率过大导致其稳定性下降，进而导致算法延缓收敛甚至不能收敛。而在群体内部，所有个体在操作上应具有同等地位，即交叉概率应相同，从而使算法在搜索空间各方向上的搜索能力达到平衡。本文设计了决定于进化代数的自适应交叉概率：

(18)

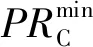
3.3.4 变异算子

在算法早期，种群具有较高的多样性，此时变异概率应该较小，以提高算法的运行速度。而随着进化的推进，群体不断向适应度高的个体不断趋近，导致种群多样性下降，此时应增大变异概率，以增强其多样性。同理，在同代种群中，不同个体的变异概率应该决定于其优劣性，应该加大优质个体变异概率，以使群体多样化。因此，本文设计与遗传进化代数和个体适应度相关的自适应变异概率：

(19)

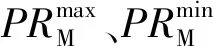
4 仿真实验

4.1 仿真实验1：算法有效性和性能验证

4.1.1 评价指标

通过以下指标来评判算法的性能优劣：

1) 调度成功率[8-9]。成功调度的任务与请求调度的任务数目之比为

SSR=Xsuc/Xtot,

(20)

式中：Xsuc为成功调度的任务总数；Xtot为请求调度的任务总数。

2) 时间偏移率[25]。成功调度任务的实际执行时刻相对于期望时刻的偏移程度，用以反映任务调度的及时性：

(21)

3) 实现价值率。常用的实现价值率指标[8-9,25]将各任务的优先级直接作为任务价值，用成功调度任务与所有请求任务的总价值相比得到指标值。这只能反映出任务调度成功率以及满足重要性原则的情况，而不能体现任务及时性对实现价值率的动态影响。因此根据本文动态价值函数，对实现价值率进行改进：

(22)

4.1.2 参数设置

调度间隔50 ms，仿真时长25 s，以目标总数来代表不同的雷达负载情况，目标数量设为10,20,…,80批。设置3个目的地A、B、C，分别对应于战略、战役、战术层级，各目标随机设置攻击目的地。不同工作方式任务的参数设置如表1所示，精密跟踪(下简称为精跟)、普通跟踪(下简称为普跟)、监视目标的数目之比为5∶3∶2，且由场景发生器对应随机产生各类目标参数，使目标威胁度满足：精跟>普跟>监视。每增加10批目标，进行100次蒙特卡洛仿真，取实验平均值。对于每一个跟踪采样，探测概率设置为1. 搜索任务为常驻任务，依编排好的波位进行，在仿真开始后按搜索间隔产生，该搜索间隔由弹道导弹穿越搜索屏的时间和搜索累积探测概率决定。

表1 任务参数设置Tab.1 Parameters setting of tasks

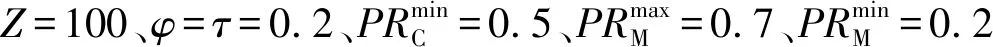
4.1.3 仿真结果及分析

图2为3种算法的调度成功率对比。3种算法的调度成功率在目标数量超过20批时都处于下降状态，其中MEDF算法的调度成功率下降最快，HPEDF算法调度成功率下降最慢，这是由于HPEDF算法能够在尽量减少删除搜索任务的情况下使更多跟踪任务被调度，因而调度成功率在3种算法中最高。在目标数目为80批时，本文算法相对于MEDF算法调度成功率提升了13%，HPEDF算法相对于MEDF算法提升了20%.

图2 调度成功率对比Fig.2 Comparison of scheduling success ratios

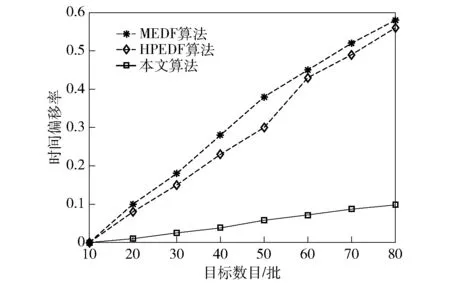
图3 时间偏移率对比Fig.3 Comparison of time shift ratios

图3为3种算法的时间偏移率对比。MEDF算法、HPEDF算法的时间偏移率上升较快，且MEDF算法的时间偏移率最高，而本文算法时间偏移率最低、上升速率最慢。这是由于MEDF算法和HPEDF算法都没有考虑到及时性因素，且MEDF算法优先对截止期临近的任务进行调度，导致其时间偏移率最高；而本文算法注重任务及时性的满足，在尽可能调度多的跟踪任务基础上，使任务贴近期望时刻被执行。当目标数目80批时，本文算法的时间偏移率相对于MEDF算法、HPEDF算法分别减小了48%和46%.

图4所示为3种算法的实现价值率对比。结合图2～图4可以看出，当调度成功率为1.0的时候，实现价值率并不一定为1.0，这是由于本文中的任务实现价值率指标不仅与成功调度的任务数目有关，还受到调度及时性的动态影响。MEDF算法的实现价值率最低，因为该算法调度成功率低，且调度过程中不仅删除搜索任务还会删除价值更高的跟踪任务。本文算法在调度成功率略低于HPEDF算法的基础上，实现价值率却比HPEDF算法更高，当目标数目80批的时候，指标提升了12%. 这是由于本文算法更能满足任务及时性要求，尤其是对于高价值任务，其时间偏移率更低。该结果说明任务调度及时性的变化对于实现价值率有重要影响。

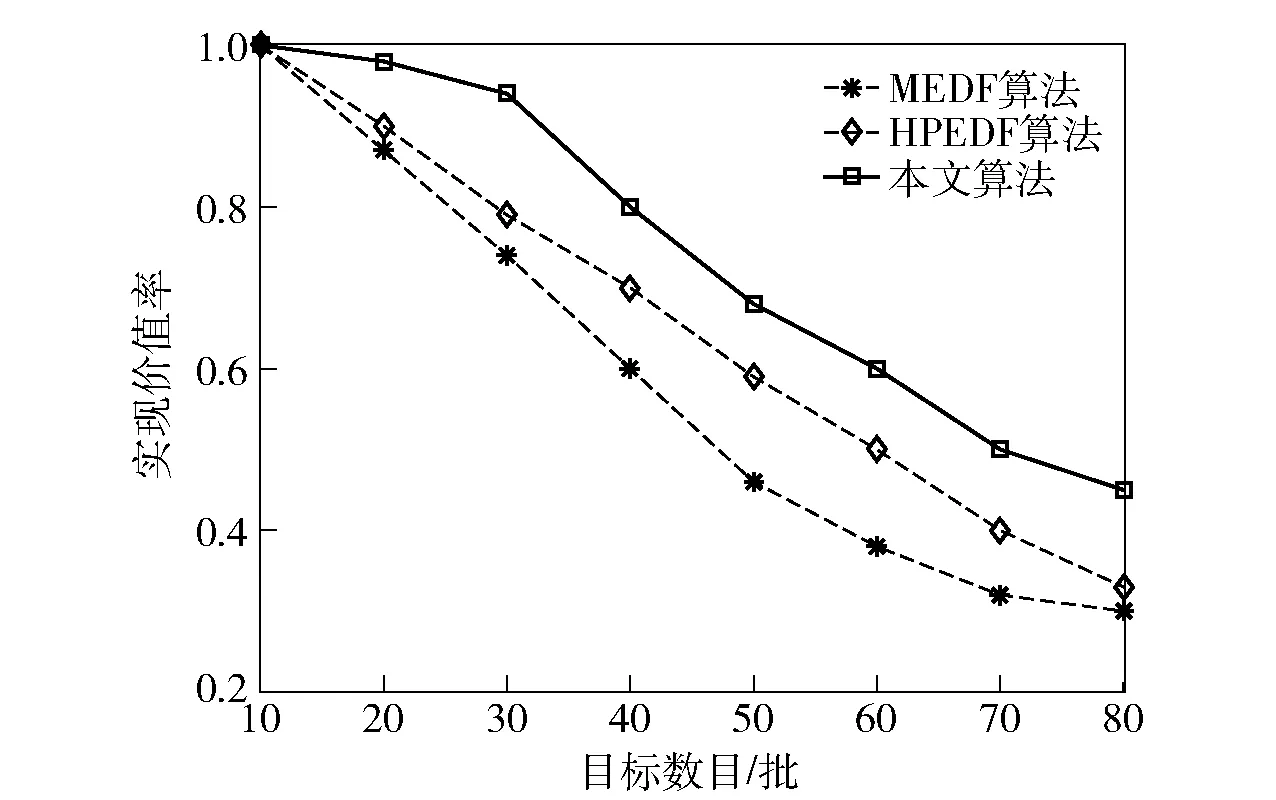
图4 实现价值率对比Fig.4 Comparison of hit value ratios

图5 不同工作方式的实现价值率对比Fig.5 Comparison of hit value ratios of different task types

图5所示为在本文算法中，不同工作方式跟踪任务的实现价值率对比。从图5可以看出，在精跟目标和普跟、监视目标数目一致的情况下，本文算法对于精跟任务的实现价值率更高，在总目标80批时达到了78%，比普跟、监视任务高47%. 这是由于本文算法利用导弹目标威胁度和截止期构建综合优先级，且威胁度占主要地位；精跟目标威胁度相对较大，优先级更高，进而最大价值更大，且执行时刻更加贴近期望时刻，产生了较好的实现价值率。这说明本文算法在保证总体调度性能的基础上，注重对高优先级任务的调度效果。

以上仿真结果表明：本文算法相比MEDF算法、HPEDF算法，能够较好满足任务调度及时性；此外，本文算法实现价值率更高，且对于高优先级任务的调度效果更加明显。

4.2 仿真实验2：价值函数参数对算法性能的影响分析

实验1中任务动态价值函数参数设置为θ=1、ξ=3.0，实验2对不同价值函数参数对算法性能的影响进行验证分析。

目标总数述设置为40批，精跟目标20批，普跟、监视目标20批。对表2所示的3种参数组合分别进行仿真，其他设置与实验1一致。对每种参数组合进行100次蒙特卡洛实验，取结果平均值。

表2 任务价值函数参数设置组合Tab.2 Parameters setting of task value function

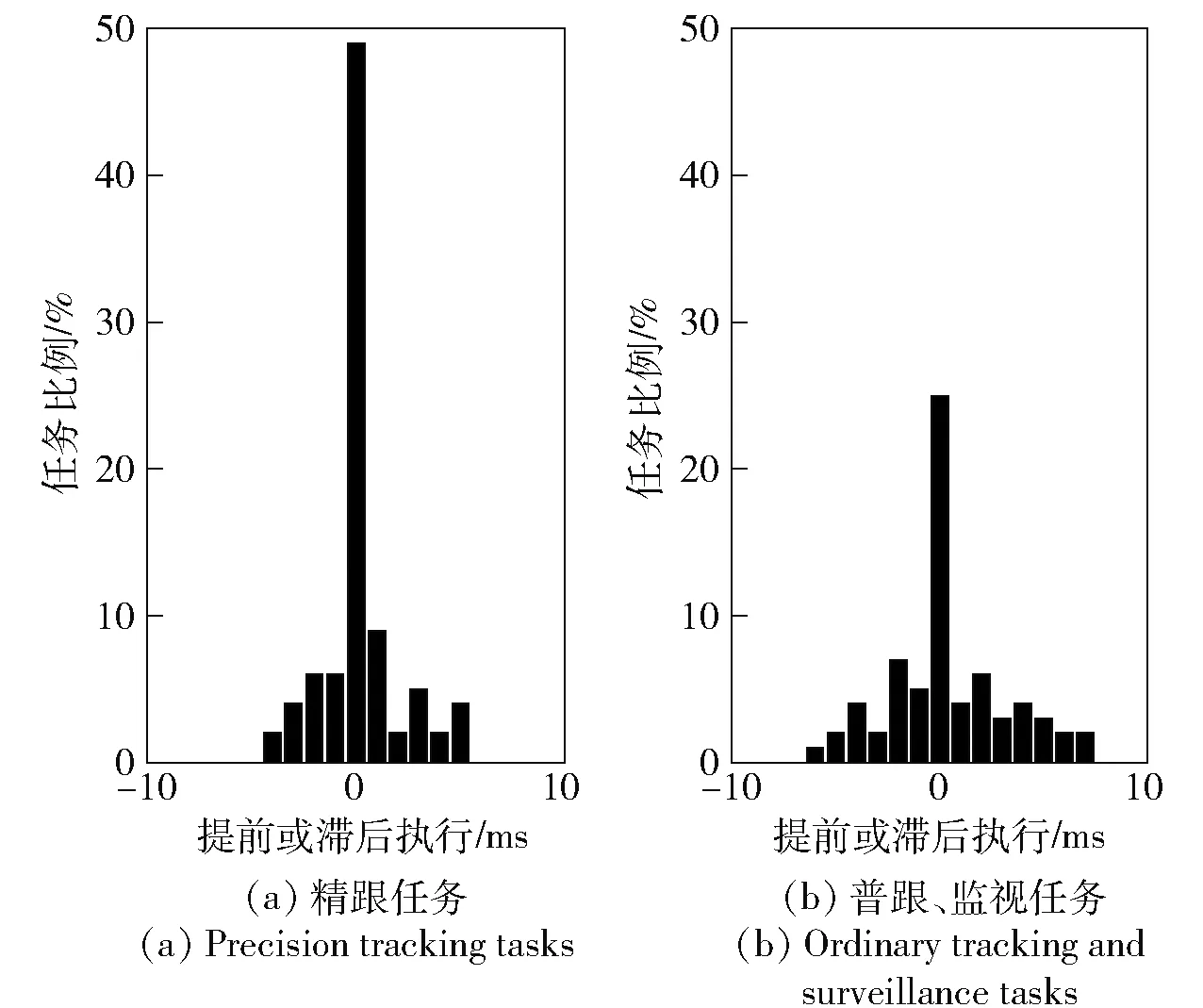
图6 组合1下任务调度偏移情况对比Fig.6 Comparison of task scheduling shifts under Combination 1

图6～图8是3种参数组合下，精跟任务以及普跟、监视任务的调度偏移情况对比，图中纵轴的任务比例表示满足横轴对应条件的任务数目在总任务数目中的占比。

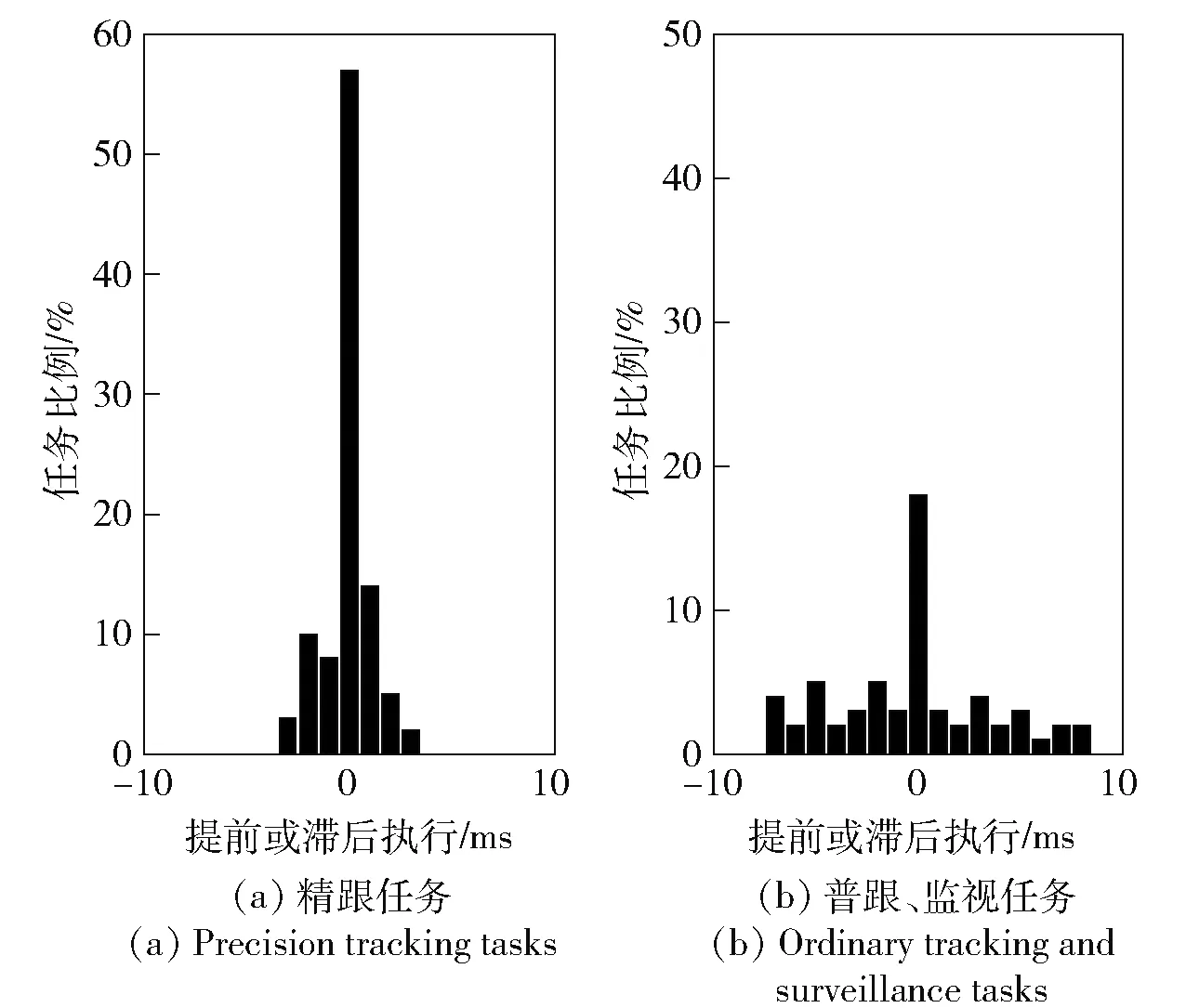
图7 组合2下任务调度偏移情况对比Fig.7 Comparison of task scheduling shifts under Combination 2

图8 组合3下任务调度偏移情况对比Fig.8 Comparison of task scheduling shifts under Combination 3

结合图6和图7可以看出，当ξ=3.0而θ不同时，θ越大，精跟任务实际执行时刻的偏移程度越小，且在期望时刻被执行的的任务比例越高，当θ=1时为49%，当θ=2时为57%. 此外θ越大，精跟任务的调度成功率越高，当θ=1时为90%，当θ=2时为99%. 而普跟、监视任务的时间偏移和调度成功率变化趋势正好相反。这是由于ξ相同时θ越大，不同优先级任务间的最大价值差异变大，调度模型以总实现价值最大为目标函数，使得高优先级的精跟任务的调度成功率增大，时间偏移率降低。

结合图6和图8可以看出，当θ=1而ξ不同时，ξ越小，精跟任务的时间偏移程度越小，且当ξ=3.0时，在期望时刻被执行的的精跟任务比例为49%，当ξ=0.5时为64%. 而低优先级任务(普跟、监视)的调度偏移程度变化呈相反趋势。这是由于θ相同时ξ越小，不同优先级任务之间的价值变化斜率差异越大，随着执行时刻的偏移，高优先级任务实现价值下降越快。因此当ξ=0.5时，为了使总实现价值最大，要减小高优先级任务也就是精跟任务的时间偏移率。

该仿真结果说明，任务动态价值函数中的参数θ、ξ对调度性能产生影响，θ越大、ξ越小，对高威胁度、高优先级任务的调度效果越好。

4.3 仿真实验3：模型求解算法性能对比

将本文的MGA与文献[29]提出的单纯形法，以及传统GA在求解调度模型时的运行时间进行对比，以对算法性能进行分析。其中，MGA参数设置与实验1保持不变，传统GA的参数设置如表3所示。

表3 GA参数设置Tab.3 Parameters setting of genetic algorithm

图9 算法平均运行时间对比Fig.9 Comparison of average running times of algorithms

进行100次蒙特卡洛仿真，取实验结果平均值，得到3种算法的平均运行时间对比如图9所示。单纯形法在求解模型时会产生最多的计算量，其运行时间最长。而MGA设置了自适应选择算子、交叉算子、变异算子，增强了对全局最优解的搜索能力和收敛速度，因此其平均运行时间小于GA. 该仿真结果说明，本文提出的MGA具有较好的求解性能。

5 结论

资源的优化调度是发挥反导预警相控阵雷达效能的关键，本文提出一种综合优先级下基于价值优化的任务调度算法，所作的主要贡献和结论如下：

1) 根据弹道导弹目标特性，结合目的地重要程度以及二者之间的相互关系，构建弹道导弹目标威胁度模型。

2) 基于任务优先级确定任务最大价值，并提出任务动态价值函数，反映出任务价值随实际执行时刻的变化规律。

3) 构建了价值优化调度模型，使任务执行时刻更贴近期望时刻，提高了任务调度及时性，更满足弹道导弹跟踪任务要求。

4) 改进了实现价值率指标，能更好反映出任务及时性对任务实现价值的影响。

5) 仿真结果表明，该算法具有有效性，能够提升任务调度及时性和实现价值率。

6) 本文将任务提前或滞后执行的价值变化斜率大小设为一致，需要进一步研究：根据提前或滞后执行对任务价值的不同影响，构建差异化的价值变化斜率函数。