基于多目标蚁群优化的单类支持向量机相似重复记录检测
吕国俊, 曹建军, 郑奇斌, 常宸, 翁年凤, 彭琮
(1.陆军工程大学 指挥控制工程学院, 江苏 南京 210007;2.国防科技大学 第六十三研究所, 江苏 南京 210007)
0 引言
随着科技、经济的迅速发展,日益增长的数据给人们的生活带来便利,与此同时,数据质量问题也日渐突显。数据清洗是通过检测、分析和修正数据中的错误或不一致来提高数据质量的有效途径[1]。由于字符错误、重复录入等原因,同一个数据源中可能包含多个相似重复记录,导致数据质量降低。针对相似重复记录的普遍性、复杂性以及对后续数据利用的影响,如何检测和消除相似重复记录一直是数据清洗研究关注的热点[2]。
现有的相似重复记录检测算法主要包括基于属性相似度的方法和基于关联关系的方法。其中基于属性相似度的方法根据属性信息的相似程度进行记录对的匹配。宋国兴等[3]提出一种基于关键属性组的相似重复记录检测方法,该方法首先通过属性间的互信息进行属性选择,然后将属性值用内码表示,根据内码序值进行聚类,最后由同一类中的内码之间的相似度进行相似重复记录匹配,该方法有效解决了记录属性维度过高带来的问题。针对高维数据噪声对检测造成的影响,宋国兴等[4]又对传统的基于空间距离的相似性度量进行改进,将属性值的接近程度作为相似性度量的依据,实验证实了该度量方法具有较高的稳定性。曹建军等[5]采用有监督的学习算法,利用支持向量机(SVM)对记录对之间的属性相似度向量进行分类,判定是否为相似重复记录,实验表明该方法具有较高的查准率和查全率,但该方法未考虑到真实数据集中相似重复记录样本稀少的问题。针对大数据来源多、维度高、体量大的特点,宋人杰等[6]对传统SimHash算法进行改进,利用倒排索引算法提高相似重复记录的匹配效率,并用MapReduce模型在云环境下实现大数据相似重复记录的并行检测和直接输出。Elziky等[7]将N-Gram索引字符串使用相应的ASCII码转化为数值,在保证相似重复记录检测准确性的条件下提高了检测效率。Samiei等[8]提出一种基于聚类的排序近邻算法,该算法解决了对于动态记录进行相似重复检测的效率问题。
基于关联关系的方法相比基于属性相似度的方法,还利用了属性间的关联关系信息(如作者和单位2个属性之间的隶属关系),拥有更高的准确性[9]。马平全等[10]利用N-Gram语言模型对记录间的潜在联系计算N-Gram值并进行排序,根据排序结果计算记录间的相似度完成相似重复记录检测。Rabia等[11]提出基于训练数据的自适应学习模型,学习了训练数据中的关系类型,增强了对问题模型的适应性;在此基础之上,谭明超等[12]提出了一种基于关系类型自适应学习方法,将权重放在关系类型上,并给出一种基于有监督学习的权重学习模型,用于降低权重学习对训练数据的要求,进一步提高准确性。
尽管当今的数据总量庞大,增长迅速。但在某些领域,数据稀缺问题仍然是大数据质量面临的重大挑战之一[13],上述相似重复记录检测算法能够完成在大数据背景下的相似重复记录检测工作,但这些算法并未考虑到真实数据源中相似重复记录稀缺的问题。不同于经典SVM分类器采用两类训练样本“间隔最大”训练超平面实现最优分类,基于支持向量的单类分类器模型的特殊性在于只有一类训练样本,这对于一些由于复杂性高,获取样本的代价高昂,数据稀缺等原因只能获取其中的一类样本的分类问题具有重要意义,如异常检测、故障诊断等[14]。
基于支持向量的单类分类器有单类支持向量机(OCSVM)和支持向量域描述(SVDD)两个经典模型[15],Scholkopf等[16]提出的OCSVM算法将特征空间零点设置为非目标类唯一的实例来构建超平面并使零点到超平面的距离最大化。Xue等[17]通过对比该分类器和经典二分类SVM的分类性能验证了OCSVM算法在进行故障诊断中的优越性。Tax等[18]提出一种软间隔的最小超球SVDD方法,该方法从特征空间中找到能够将所有训练样本包含在其中的最小超球面,继而通过测试样本和超球面的位置关系进行分类。针对SVDD对非球型目标样本包裹紧凑性的问题,Wei等[19]利用超椭球代替SVDD中的超球以适应目标样本映射到特征空间后的结构信息。Burnaev等[20]对OCSVM和SVDD等两种方法在训练目标样本、构建松弛变量时引入额外的信息(如图像分类时的文本描述信息、恶意软件检测时的源代码信息等)来细化分离边界的位置、提高异常检测的准确性。
针对真实数据源中相似重复记录稀缺的问题,使用OCSVM实现对相似重复记录的分类检测。其中考虑到记录的特征个数对于分类效果的影响,利用多目标蚁群算法进行特征选择,实现分类效果优化。
本文第1节介绍OCSVM单类分类器模型的方法并给出相似重复记录检测问题描述;第2节结合单类训练样本特点,设计了求解最优属性子集的多目标蚁群优化算法,实现了对记录属性的特征选择;第3节实验部分给出该重复记录检测方法的效果和效率验证;第4节进行总结。
1 方法描述
1.1 基于OCSVM的单类分类器模型
OCSVM通过实现该类样本与特征空间零点之间的“间隔最大”构造分离超平面,并且最大化分离超平面到零点的距离。模型如(1)式:

(1)
ξi≥0,
式中:w为高维空间分离超平面的法向量;Φ(xi)为一个将特征向量xi映射到高维特征空间中的特征投影函数;d为空间零点到分离超平面的距离;ξi为松弛变量;s为样本总数;ν为正则化系数。采用拉格朗日乘子法对模型进行求解,将核函数带入得到最终函数模型:

(2)
式中:αi为拉格朗日乘子;K(x,xi)为核函数。本文采用径向基核函数(RBF),2个样本xi和xj之间的核函数定义为
K(xi-xj)=exp (-γ‖xi-xj‖2),γ>0,
(3)
式中:γ为设置的内核传播参数。
OCSVM创建了一个参数为w和d的超平面,该超平面与特征空间中的零点距离最大,并且将零点与所有的训练数据点分开,如图1所示。图1中:O为空间内坐标零点;l为OCSVM创建的超平面,能够将零点与训练样本分开且保证零点到超平面的距离最大;l1、l2为其他超平面。
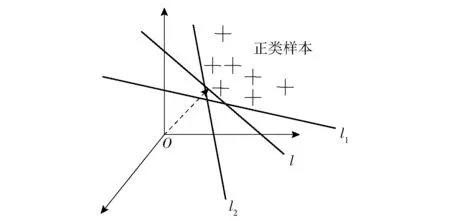
图1 OCSVM超平面构造图Fig.1 OCSVM hyperplane structure
利用基于OCSVM的单类分类器模型能够在缺少负类样本情况下进行有效分类的特性,结合真实数据源中相似重复记录样本稀少的实际,将不相似重复记录对的属性相似度向量作为正类样本,输入到分类器中进行训练,学习到不相似重复记录对的统一特征,并具备对于不相似重复记录对的分类能力。然后用训练好的分类器对样本对的相似度向量进行分类,相似重复记录对的向量由于不符合学习到的统一特征,会被分类到超平面的另一侧,因此完成对相似重复记录的有效检测。
1.2 问题描述
对2条记录进行相似重复记录检测,首先计算2条记录对应属性值的相似度,再根据各属性值的相似度计算2条记录的相似程度,并判断它们是否相似重复(匹配或不匹配)。文献[5]将该过程看成一个二分类的过程,以一个记录对的属性相似度向量作为传统二分类SVM的输入,将其分为相似重复(匹配)和不相似重复(不匹配)两类。但该方法需要足够的相似重复记录样本对进行训练,而真实数据集中相似重复记录数量稀少,制约了传统SVM的训练效果及分类检测性能。根据1.1节的单类分类器模型只需要一类样本参与训练的分类特点,结合真实数据集中,相似重复记录数量远小于不相似重复记录数量的实际,提出基于OCSVM单类分类器的相似重复记录检测方法。相似重复记录检测流程如图2所示。

图2 相似重复记录检测流程图Fig.2 Flow chart of similar duplicate record detection
本文提出的方法和文献[5]的方法流程区别在于分类器的选择,文献[5]使用的是传统二分类SVM进行分类,训练时需要相似重复记录对和不相似重复记录对两类样本;本文考虑到真实数据集中相似重复记录个数稀少的实际,采用OCSVM进行分类,只需不相似重复记录对这一类样本进行训练。
2 多目标蚁群算法特征选择
2.1 特征选择模型
在高维度的特征集中,冗余特征的存在往往严重影响着分类效率和效果[21]。在相似重复记录检测中亦是如此,冗余的属性信息的存在给相似重复记录的准确分类造成困难。特征选择通过构建最优特征子集来消除数据中的冗余信息,减小运算复杂度,实现分类效率效果最优。
对于相似重复记录检测算法效果的评价指标主要有4个:查准率P、查全率R、分类正确率A和F1指标。分别为
(4)
(5)
(6)
(7)
式中:TN为检测出的真的相似重复记录对数;TP为检测出的真的不相似重复记录对数;FN为检测出的假的相似重复记录对数;FP为检测出的假的不相似重复记录对数。
通常,查准率和查全率不能同时达到最优,对采用查准率和查全率为主要评价指标的相似重复记录分类检测算法,可以将特征选择问题描述为:从属性集A中选择一个基数为q的属性子集Aq,使由Aq所包含属性生成的相似特征向量的相似重复检测查准率和查全率综合达到最优,同时Aq规模最小。即对相似特征向量的特征进行选择的过程,其数学模型为
(8)
(9)
minq,
(10)
s.t. |Aq|=q,1≤q≤q′,
式中:Λ(Aq)表示以属性子集Aq生成的相似特征向量为输入的分类器Λ的分类结果,根据(8)式和(9)式,由测试样本计算可得;q′表示属性集A中的属性总数。(8)式~(10)式表示基于Aq的相似重复记录检测结果的查全率和查准率最大,同时使Aq的规模最小,其中(8)式和(9)式的优先级大于(10)式。因此,相似重复记录的特征选择是一个多目标的子集问题。
2.2 模型的蚁群算法求解
多目标问题通常并不存在各目标都为全局最优的解的情况,而存在一非劣解集,称为Pareto最优解集,多目标优化的目的是力求找出一组解,尽可能全面地逼近Pareto解集,决策者可按需求进行评价,选出适用的满意解[22]。
一类基于元启发式算法全局搜索的次优子集求法得到了快速发展与应用,如蚁群算法、模拟退火算法、遗传算法、人工免疫算法、粒子群算法、蝙蝠算法、萤火虫算法等[23]。
蚁群算法是一种元启发式算法,由于其具有很强的求解较好解的能力、较好的鲁棒性、信息正反馈、并行分布式计算及易于与其他启发式方法相结合等优点[24],在短期内得到迅速发展,应用领域也不断扩大,特别是在求解复杂多目标组合优化问题方面显示了其优越性。Dorigo等[25]将蚁群算法与模拟退火、进化规划、遗传算法、模拟- 遗传算法进行了比较,发现蚁群算法在解决经典的组合最优化问题——旅行商问题时优于其他算法。
本节中以相似重复记录检测的查准率和查全率作为优化目标,对于给定的q值,求出(8)式、(9)式模型的满意解,采用多目标蚁群算法求解,步骤如下:
步骤1引入基于图的蚂蚁系统[26],根据相似重复记录检测特征选择问题构造有向图。蚂蚁根据有向图边上的信息素值与静态启发式信息构建可行解。如图3所示的特征选择问题的构造图中,在t时刻v1处生成M只蚂蚁。每只蚂蚁根据边的信息素和启发式信息独立的选择某一条路径向下一个节点移动,其中c为特征总数,n为蚂蚁在一次搜索中寻找解的个数,eij表示蚂蚁在第j步选择第i个特征。

图3 特征选择问题构造图Fig.3 Construction diagram of feature selection
步骤2引用文献[5]中蚂蚁选择路径的路径转移概率公式来实现图3中蚂蚁的概率转移,如(11)式所示,
(11)
式中:ebj表示蚂蚁在第j步选择第b个特征;禁忌表tabum为第m只蚂蚁走过的边,即蚂蚁已经选择的特征;α和β分别为信息素重要程度和启发式信息重要程度的系数;τij(t-1)为在t-1(t=1,2,3,…)时刻的边eij上的信息素量;τbj(i-1)为在t-1(t=1,2,3,…)时刻的边ebj上的信息素量;ηb为选择第b个特征的期望程度。由于需要同时优化查准率和查全率2个目标,对其分别设置信息素矩阵,在计算转移概率中的τij(t-1)时,采用(12)式2个信息素矩阵进行聚合:
(12)

(13)
式中:σi为不相似重复类内第i个相似特征值的标准差。在只有一类样本的条件下,无法像线性判别分析那样通过度量多类情况中利用类间信息选择特征,(13)式表明,只通过类内散度的最小化来选择特征,即算法优先选择最小化单类训练样本离散程度(即标准差小)的特征。
步骤3当蚂蚁每次迭代完毕后,按照(14)式和(15)式分别对查准率信息素矩阵和查全率信息素矩阵进行更新:
(14)
(15)
式中:ρ为信息素挥发系数;tabut为t时刻选择的特征路径;Δ′(tabut)为信息素更新增量,计算公式为
(16)
F(tabut)为对应更新的信息素矩阵的目标函数值,Q为常数(根据ρ值确定,主要调节信息素增量的大小)。
通过对于不同q值求得的Pareto解集进行比较更新,移除支配解,在最后的Pareto解集中选取特征个数最少的解,保证特征规模的最小化。
求解多目标蚁群算法优化模型的算法描述如下:
算法1. 多目标蚁群算法进行特征选择
输入:候选特征集,待求特征子集中特征个数范围、蚁群算法相关初始化参数
输出:特征子集的Pareto解集
Begin
初始化
forq=1∶10
{fori=1:ite
{生成M只蚂蚁用于搜索
form=1∶M
{根据(11)式计算转移路径概率,选择特征;
用被选的特征进行OCSVM训练和测试;
保存解;
}
移除非支配解
fornum=1∶2
{根据(14)式和(15)式更新信息素矩阵;
}
}
Pareto解集存储
}
不同q值的Pareto解集比较更新,移除非支配解
输出Pareto解集
End.
3 实验仿真
3.1 实验数据及预处理
本文的实验数据来源于文献[5]中的某信息系统的人员基本情况表pst和UCI机器学习数据库中的adult数据集。按照相似重复记录的比例不同,对这两个数据集分别以10%、5%、2%的相似重复记录占比进行数据集划分。
对数据集进行预处理,引用文献[5]中对记录内字符串型、枚举型、日期型等不同类型属性的相似度计算方法,计算数据集中记录对之间的相似特征向量。
3.2 仿真结果及分析
3.2.1 参数设置
实验中所用各个算法的参数信息如表1所示。

表1 参数信息表Tab.1 Algorithm parameters
注:k为训练数据的特征个数。
3.2.2 实验设置及结果分析
为选择较好的分类方式,实验对比OCSVM[16]和SVDD[18]这两种基于支持向量的单类分类算法的相似重复记录检测结果,其中,不相似重复记录对为正类样本,相似重复记录对为负类样本。实验采用5重交叉检验取均值的方法[27],以消除由于训练集和测试集划分所得结果的偶然性,有助于评估模型的稳定性。评价指标为F1值、查准率、查全率和分类正确率。对于两个单类分类器模型,通过采用网格搜索的方法得到各算法的参数如表1所示,确保OCSVM和SVDD算法能够在实验过程中达到较优的分类效果。
表2中的实验结果均为5重交叉检验后的均值。对其进行分析,发现数据集不同,得到的F1值的结果也不一样,对比发现,使用OCSVM分类效果略好于使用SVDD的分类效果,每一个数据集测试结果的查准率和查全率能够同时取得较优的结果。但是,对于数据集pst5%而言,SVDD的结果略好于OCSVM,尤其在查准率指标上,SVDD能够得到最优的结果1.000 0,可能是因为该数据集具有更特殊的数据分布(正类样本更趋于球体分布)。
通过对比不同相似重复比率进行数据划分后的分类结果,可以发现,数据中正负类的不平衡程度对于OCSVM和SVDD这样的单类分类器分类结果影响不大,各个指标上的小幅波动是由于划分后的数据集中数据分布不同所导致。
为测试单类分类器OCSVM、SVDD在解决相似重复记录检测问题的有效性,实验对比了OCSVM、SVDD和在训练数据中不同正负类样本数目比例下的传统二分类SVM的分类结果。在pst数据集上,采用5重交叉检验取均值的方法,其中OCSVM、SVDD采用80个正类样本进行训练,传统SVM在此基础上随机加入不同比例个数的负类样本进行训练。所得分类结果的F1值对比如图4所示。图4中:横坐标N表示传统SVM训练样本中正负类样本的比率,N越大表示训练样本中正负类的数目越不平衡(负类样本的数目相比正类样本越少);纵坐标表示(7)式中的F1值;F1值越大说明分类效果越好。从图4中可以看出:OCSVM的分类效果要优于SVDD的分类效果;其次,当N≥8时,OCSVM和SVDD的分类效果要优于传统SVM的分类效果,且这个优势在N=16,N=20时更加明显,而当N=40,N=80时,由于训练时负类样本数目过少,不能分类出负类样本,才出现F1值最小的情况。结果表明,当对数据进行分类时,如果能够用于训练的负类样本数很少,采用OCSVM、SVDD的单类分类器的分类效果要远好于采用传统SVM的二分类器的分类效果。有效弥补了文献[5]中在用传统SVM分类解决真实数据集时负类样本少,难获取的问题。
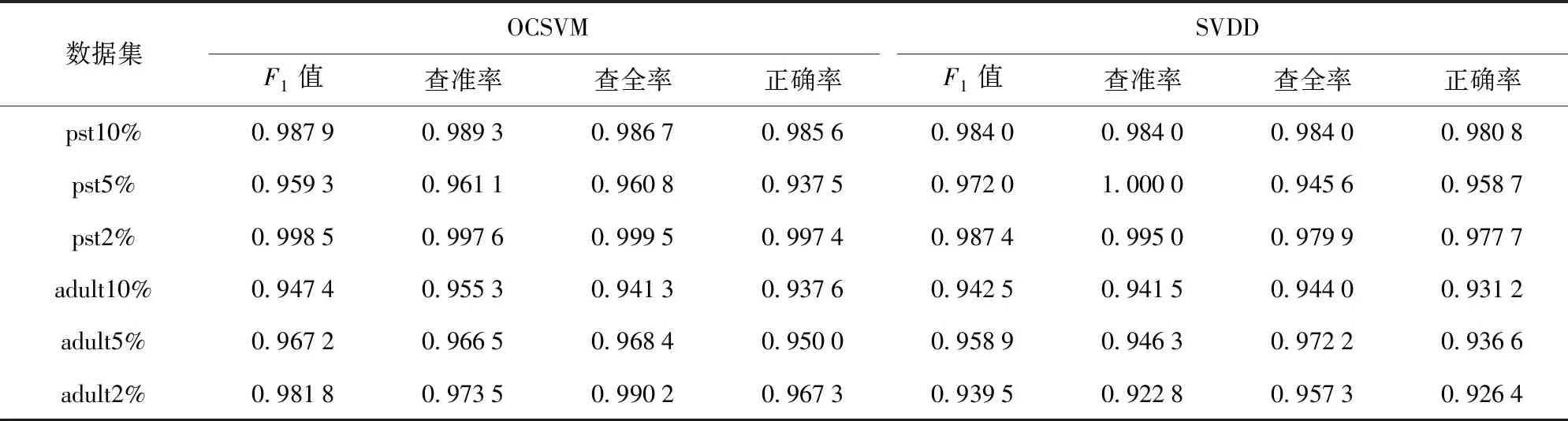
表2 OCSVM对比SVDD仿真结果Tab.2 Comparison of simulated results of OCSVM and SVDD

图4 OCSVM、SVDD和传统SVM的F1值比较Fig.4 Comparison of F1 values of OCSVM, SVDD and traditional SVM

图5 OCSVM、SVDD和SVM的正确率比较Fig.5 Comparison of classification accuracies of OCSVM, SVDD and traditional SVM
类似的结论从图5中也可以得出,相较于F1值,图5的纵坐标为分类正确率。当N≥8时,OCSVM的分类正确率要优于传统SVM;当N=40,N=80时,由于缺少负类信息,导致传统SVM不能分类出负类样本。
3种算法的时间效率由图6给出,从图6中可以看出,OCSVM算法的时间效率要小于SVDD,N越小时,传统SVM的训练时间越大,这是因为N越小时,训练样本的总个数越大,算法所消耗的时间也越大。
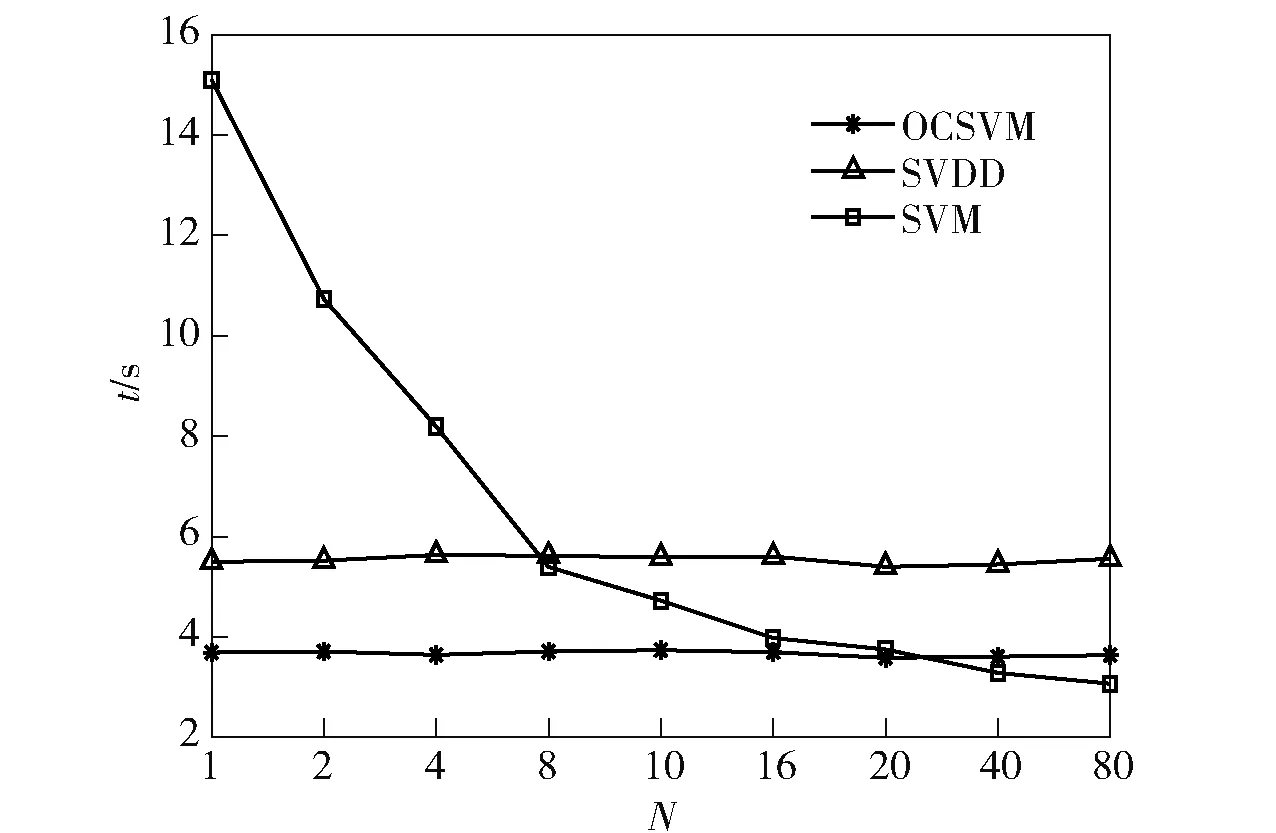
图6 OCSVM、SVDD和传统SVM的时间效率比较Fig.6 Comparison of time efficiencies of OCSVM, SVDD and traditional SVM
针对相似重复记录的样本数远小于不相似重复记录的样本数N≥8,采用传统SVM分类需要一定量的相似重复类样本,不符合真实数据集中相似重复记录个数稀少的实际,故使用OCSVM、SVDD分类相比传统SVM分类更行之有效。
4 结论
本文根据数据源中样本记录对是否相似,将相似重复记录检测看成二分类问题,针对相似重复记录样本稀少的实际,利用OCSVM单类分类器分类,并使用多目标蚁群算法进行特征选择优化。得到主要结论如下:
1)利用OCSVM单类分类器进行分类,解决了真实数据源中相似重复记录样本少、难获取的问题。
2)设计启发式因子为类内散度最小化约束的多目标蚁群算法特征选择优化模型,综合考虑算法的查准率、查全率和特征规模,得到了较优的分类效果。
3)本文方法在数据源中相似重复记录样本稀少情况下的效果优于传统二分类SVM分类方法,具有更好的适用性。
在当今大数据发展的背景之下,数据稀缺问题仍然是大数据质量不可忽视的挑战之一。本文提出的方法能有效解决数据源中相似重复记录样本稀缺的问题,实现相似重复记录检测。

