结构可靠性优化的通用生成函数- 序列优化与可靠性评估方法

朱达伟, 周金宇, 庄百亮

(1.江苏理工学院 机械工程学院， 江苏 常州 213001；2.金陵科技学院 机电工程学院， 江苏 南京 211169；3.机械科学研究总院江苏分院有限公司， 江苏 常州 213001)

0 引言

随着结构设计领域研究的不断发展，传统确定性结构优化设计由于未考虑到实际工程应用中诸多不确定因素，该类设计方法正逐渐被结构可靠性优化设计(RBDO)方法取代。目前，结构可靠性优化领域的研究方法主要分为3大类：双循环法、单循环法、解耦法。

双循环法的外层是一个传统的确定性优化问题，在约束条件下使目标函数值最小，而内层的可靠性分析同样是一个在外层优化要求概率约束评价时进行的优化问题[1],内层可靠性分析步骤常采用的典型方法有可靠指标法[2]和功能度量法[3]。双循环法具有概念清晰、求解简单及稳定性高的优点，但由于工程问题越来越复杂，此类方法存在计算量庞大、效率低下等缺点，已不能满足实际工程需求。2018年，Hao等[4]基于等几何分析建立了一个高效准确的RBDO框架，用于解决复杂的工程问题。此外，为了提高RBDO的效率，提出了增强步长调整迭代算法和基于2阶可靠性分析的逐步增强顺序优化与可靠性评估方法。单循环优化方法依据约束的KKT条件重新构建可靠性优化模型，将概率约束近似等价为确定性约束，可极大提升优化效率。常用的单循环优化方法主要有：单循环单向量法[5]、基于性能测度法的RBDO单回路优化方法(SLA)[6]和基于响应面的单循环法[7]。单循环优化策略虽然大幅度提升了计算效率，但由于使用了近似等效的概率约束，求解精度难以得到保障。为了在保证求解精度的同时提高工程问题的求解效率，大量学者专注于结构优化与可靠性分析问题的解耦研究。Du等[8]提出了序列优化与可靠性评估(SORA)方法；程耿东等[9]提出序列近似规划算法；Zou等[10]提出了一种高效的直接解耦方法；Chen等[11]提出了自适应解耦方法；Torii等[12]提出一种适用于不同可靠性分析方法的RBDO解耦策略；袁修开等[13]提出一种基于灵敏度的解耦方法。解耦法虽极大程度地提高了优化效率，尤其是SORA方法被认为是最具有发展潜力的优化算法。但由于1阶可靠性法(FORM)、2阶可靠性法(SORM)等传统可靠性分析方法的固有局限，优化求解的精度问题依然普遍存在。同时，此类方法在解决功能函数为高度非线性问题时，优化结果可能会出现周期性振荡、混沌以及不收敛现象。

针对上述研究存在的问题，本文引入通用生成函数(UGF)，提出一种基于通用生成函数的序列优化与可靠性评估(UGF-SORA)方法。解决了由于FORM导致的优化精度低问题，以及解决了功能函数为高度非线性时优化结果无法收敛问题，可在保证优化效率的同时显著提升优化精度。

需要指出的是，本文所提UGF-SORA算法，由于将UGF法引入可靠性分析环节，在原理上，避开了随机变量的正态假设和功能函数的线性假设，采用离散化状态枚举，当离散步长足够小时可达到较高的计算精度。但伴随随机变量的离散化状态变多，UGF复合运算的计算量必然庞大，从而导致优化效率降低。研究表明，通过合并同类项或K均值聚类等操作有望解决优化效率降低的问题。

1 基于SORA的结构可靠性优化方法

结构可靠性优化的目的在于保证结构可靠性的前提下最小化目标函数，通常基于可靠性的结构优化模型可表述为

(1)

(2)

正如模型(1)式和(2)式所示，可靠性优化问题是一类包含可靠性分析与结构优化的双环嵌套问题，每次外层优化均伴随内层的可靠性分析。SORA方法将可靠性优化问题解耦，使得结构优化与可靠性分析的求解依次进行，极大减少了计算量。其优化模型表述为

(3)

(4)

(5)

式中：XMPP为真实物理空间的最小功能目标点；uMPP为标准正态空间中的最小功能目标点；T表示逆变换。

由于可靠指标的求解在标准正态空间中进行，所以需要将不服从标准正态分布的随机向量X转化为服从标准正态分布的随机向量u. (5)式中XMPP由标准正态空间中的最小功能目标点uMPP进行逆变换T得到。uMPP可通过以下模型求解：

(6)

式中：βt为许可可靠度指标。

图1 SORA优化原理示意图Fig.1 Schematic diagram of SORA optimization

SORA方法虽极大提高了优化效率，但可靠性分析环节通常由逆可靠性分析方法完成，对于一些随机变量类型为非高斯或离散型的问题，逆可靠性分析方法带来精度降低的问题不可避免，同时优化结果会出现混沌、震荡及不收敛现象。

2 基于UGF的结构可靠性分析方法

1986年，USHAKOV[14]首次提出了UGF的概念。目前，基于UGF的可靠性研究主要集中在多状态系统可靠性方面，对于在结构可靠性分析方面的研究尚少。主要是由于UGF研究对象多为离散型随机变量，而大部分机械结构分析所用的随机变量多用连续概率分布函数来表述[15]。本节阐述了利用UGF方法进行结构可靠性分析的原理。

2.1 随机变量的UGF

2.1.1 离散型随机变量UGF

设Xi(i=1,2,…,n)为离散型随机变量，其可能取值记为(xi1,xi2,…,xim)，相应的取值概率分别记为(pi1,pi2,…,pim). 可根据已知信息直接定义随机变量Xi的UGF如下：

(7)

式中：UXi(z)为随机变量Xi的UGF；xij为第i个随机变量的第j个状态值；pij为对应状态值的取值概率；n为随机变量个数 ；m为离散状态总数。

2.1.2 连续型随机变量UGF

在建立连续型随机变量UGF时，由于UGF是针对离散变量的，因此须将连续型随机变量离散化。设有n个连续型随机变量Xi(i=1,2,…,n)，各变量的分布函数和概率密度函数分别为Fi(x)和fi(x). 将变量Xi离散为m个点，根据失效概率的求解公式可以得到各离散点xij对应的取值概率pij为

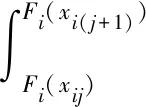
(8)

因此，可以定义连续型随机变量Xi的UGF为

(9)

2.2 多元随机变量可靠性分析的UGF法

设有连续型随机变量X1和X2，需对其进行离散化。由离散化思想可得随机变量的状态值及其对应的取值概率分别为{(x11,p11),(x12,p12),…,(x1m,p1m)}和{(x21,p21),(x22,p22),…,(x2m,p2m)}. 进行结构可靠性分析时，通常用功能函数来描述随机变量和结构系统性能之间的关系。在UGF中，常用性能结构函数Φ来描述系统各单元与系统性能之间的关系。需要指出的是，将UGF法用于结构可靠性分析时，性能结构函数即为功能函数。类比功能函数与结构可靠性之间的关系可知：当性能结构函数小于等于0时，结构失效；当其大于0时，结构可靠。将随机变量的UGF分为状态项和概率项，不同随机变量的状态项之间视情况根据结构函数Φ进行随机组合，可定义结构系统的UGF为UΦ(z)，表达式如下：

(10)

式中：⊗为复合算子，用来描述不同UGF之间的运算规则；多项式的指数项为各级结构函数所处的状态，称为状态项；多项式的系数项为结构处于某种状态的概率值，称为概率项。

结构系统的UGF蕴含着必要的性能概率分布信息，可用来计算各类可靠性指标[15]。设结构系统的UGF为

(11)

对该UGF的系数项在一定条件下进行求和，即可得到结构系统的可靠度，如下式所示：

(12)

式中：δ(·)为条件求和算子；y为结构可靠和失效两种状态的临界值；C(xi-y)为事件的示性函数，当xi>y时，值为1，否则值为0.

若随机变量个数较多，在进行UGF复合运算时可能导致运算复杂、计算量急剧增大。通常，不同随机变量的状态值会存在xi≈xj情况。此时可将对应的pizxi和pjzxj视为同类项，并进行合并同类项操作。将两项合并为(pi+pj)zxi. 一般地，由于结构函数具有递推性、可分性和互换性，使用UGF法进行可靠性分析时可实现随机信息从细观向宏观的跨尺度精确传递，且能避免由于忽略非正态性而导致的分析误差。同时结合合并同类项操作，有望在确保分析精度的条件下大规模缩减计算量[16]。

3 基于UGF-SORA的结构可靠性优化方法

基于UGF-SORA的结构可靠性优化方法是将UGF与传统的SORA算法相结合，利用与SORA算法具有相同物理意义的偏移向量s来改变确定性约束边界，以保证最小功能目标点落在可行域内。所提方法将传统嵌套优化问题转化为一系列确定性优化和可靠性分析顺序执行的序列优化问题，从而实现解耦。该方法分为3个环节来求解结构可靠性优化问题。

3.1 偏移向量的定义与更新策略

由SORA算法可以发现，每次偏移向量s迭代运算后，可得到当前优化设计向量d，通过可靠性分析环节进一步得到该设计点对应的可靠度指标β. 即可得到如下映射关系：

s→d,

(13)

d→β.

(14)

结合(13)式和(14)式可知，偏移向量s与结构可靠度指标β存在映射关系。因此可定义偏移向量s和可靠度指标β之间的函数关系式J，将函数J称为偏移函数，如(15)式所示：

β=J(s),

(15)

式中的偏移向量s为一系列未知数据，为得到该数据，可建立一种偏移向量更新策略。其数学模型如下式所示：

finds,

(16)

min|βt-J(s)|,

(17)

s.t.βt-J(s)≤0.

(18)

该策略为一确定性优化问题，将s作为设计向量，使得拟合所得的近似可靠度指标J(s)逼近许可靠度指标βt，并保证J(s)≥βt. (16)式～(18)式可通过序列二次规划等确定性优化算法求解。

3.2 偏移函数J的拟合

由于J为隐式函数，可考虑使用多项式构造响应面来近似该隐式函数，通过合理选取试验点和迭代策略，可以保证多项式函数能够在概率上收敛于真实的隐式函数[17-18]。由于不含交叉项的一次和二次响应面结构简单、运算量小、精度相对较高而被广泛应用，其表达式为

(19)

(20)

首先需要确定n+1个初始偏移向量组的各分量，本文采用下列模型获取初始偏移向量组的各分量[19]：

(21)

式中：μXi为随机变量Xi的均值；α为满足一定求解规律的特定系数，其取值尚无学者提出标准的确定方式，Bucher等[20]指出其值在±1倍随机变量变异系数区间内时较为合理。

得到初始偏移向量组后，分别根据各分量进行确定性优化求解，得到各偏移向量对应的设计点。针对每个设计点，通过UGF法完成对应结构系统的可靠性分析，得到相应的可靠度指标，即可确定s(0)与β(0)数据对。

确定s(0)和β(0)后，利用最小二乘法求解待定系数，拟合可靠度指标的线性近似值与其偏移向量之间的函数关系式。得到初始偏移函数J0(s)后，通过(16)式～(18)式求解新偏移向量，并求得该偏移向量对应的可靠度指标。下次循环时，将新偏移向量和新可靠度指标合并到初始偏移向量组s(0)和初始可靠度指标组β(0)中，构成n+2个偏移向量以及可靠度指标。此时，利用n+2对数据结合最小二乘法重新拟合偏移函数。

3.3 确定性优化求解与可靠性评估

在得到初始偏移函数后，根据(3)式和(4)式进行确定性优化求解，并且通过UGF方法进行可靠性分析，计算此时的结构可靠度指标。若不满足相关约束要求，需更新偏移函数并再次进行偏移向量的优化求解。

该方法的求解步骤如下：

步骤2通过(16)式～(18)式求解偏移向量；

步骤3通过(3)式和(4)式进行确定性优化求解，得到偏移向量对应的最优设计向量(d1,d2,…,dn)；

步骤4根据已有数据，使用UGF法进行可靠性分析，得到该设计点对应的结构可靠度指标；

步骤5根据(19)式或(20)式，利用最小二乘法重新构建偏移函数J(s)；

步骤6判断该设计点对应的可靠度指标是否满足许可可靠度指标要求并收敛。若满足，则该点即为最优设计向量；若不满足，则重复步骤2～步骤6.

基于UGF-SORA法的结构可靠性优化流程图如图2所示。

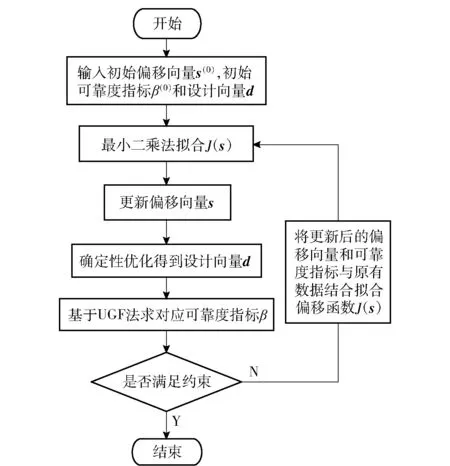
图2 基于UGF-SORA法的结构可靠性优化流程图Fig.2 Flow chart of structural reliability optimization based on UGF-SORA method

4 算例分析及讨论

本节通过不同类别的数值算例证实了所提方法相对于现有算法的优越性。由于算法的优化精度主要体现在优化结果的可靠度指标上，所以可利用目标设计点处的可靠度指标与许可可靠度指标之间的相对误差ε来比较不同算法的优化精度，ε的计算公式为

(22)

式中：βMCS为使用蒙特卡罗模拟(MCS)法(模拟次数取106)在设计点处对结构进行可靠性分析时，各设计点对应的结构可靠度指标。

算例求解时，确定性优化问题均使用优化软件包FMINCON解决，其中迭代的收敛准则设置为：相邻两次迭代目标函数值之间的相对误差小于10-6. 可靠性分析求解的收敛准则设置为：相邻两次求解所得可靠度指标值之间的相对误差小于10-3.

4.1 算例1

该算例有两个随机变量，且均服从正态分布，是一个功能函数为低阶非线性的简单可靠性优化问题。其数学模型为

(23)

该算例使用本文所提方法进行计算时，确定性优化求解均使用序列二次规划(SQP)算法，迭代过程见表1. 同时，使用其他结构可靠性优化算法的结果在表2中列出，用以分析比较。需要指出的是，表中所得数据结果都是在MATLAB R2016a软件中编程求解到，所使用机器为3.3 GHz处理器和4 GB内存的计算机。

此算例中，使用了基于HL-RF法、改进均值法(AMV)的双循环优化算法、属于单循环法的SLA算法以及属于解耦法的SORA算法与本文所提算法进行比较。由表2可以得知，传统结构可靠性优化方法众多，其优缺点也各异。在实际工程应用中，设计点的可靠度指标越接近许可可靠指标越好，其既满足了结构的使用需求，又减少了由于可靠性过高带来的额外设计成本。本文通过(22)式的相对误差ε来体现优化结果的可靠度指标是否接近许可可靠度指标。对比表2中的数据可以发现，本文所提UGF-SORA法优化结果的ε远远小于其他算法，说明该方法的优化精度显然高于其他优化算法。

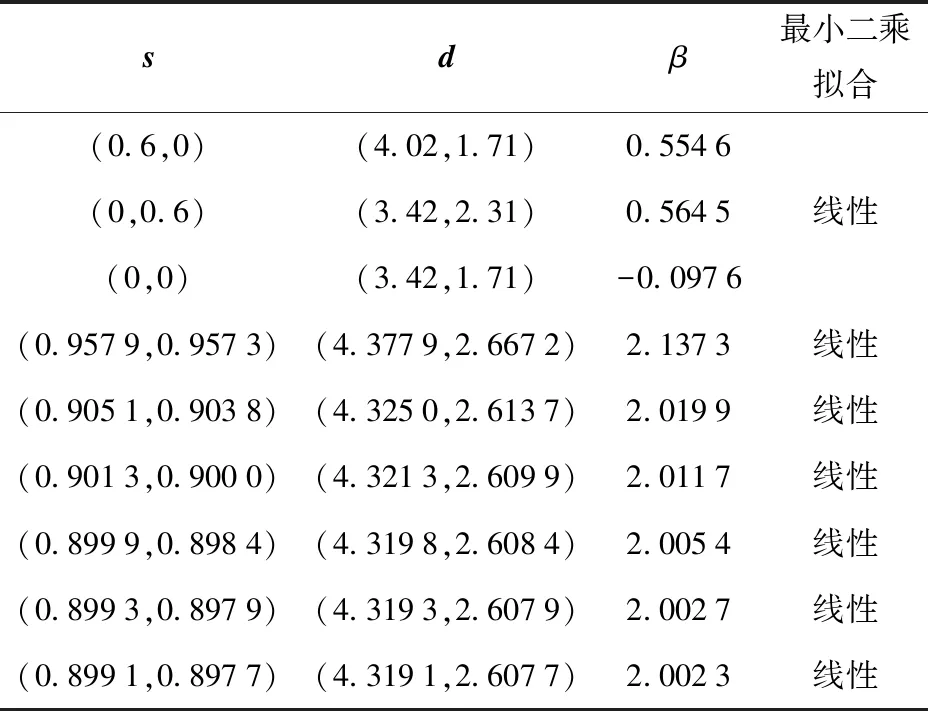
表1 UGF-SORA方法迭代过程Tab.1 Iterative process of UGF-SORA method

表2 算例1不同结构可靠性优化方法优化 结果对比Tab.2 Comparison of optimized results of reliability optimization methods for different structures in Example 1

从表1中可以看出，收敛解处的可靠度指标为2.002 3，该值十分接近表2中使用MCS方法进行可靠性分析所得值2.008 0，但使用MCS法进行一次可靠性分析就需要106次模拟次数。由此可见，得到同样高精度的可靠度指标情况下，基于UGF法进行可靠性分析的效率明显高于MCS法。同时，结合合并同类项操作的UGF-SORA算法所需调用功能函数的次数为378，相较表中所列其他传统算法，其优化效率较低，但在可接受范围内。

4.2 算例2

该算例有两个随机变量，且均服从正态分布，但功能函数为高度非线性。其数学模型为

(24)

表3 算例2不同结构可靠性优化方法优化结果对比Tab.3 Comparison of optimized results of reliability optimization methods for different structures in Example 2

由表3中数据可以发现，对于功能函数为高度非线性的优化问题，大部分算法如AMV算法、SLA算法、SORA算法均无法得到收敛解。而本文所提方法，可靠性分析环节由UGF法完成，可以良好地解决此类问题。同时，与基于HL-RF算法的双循环法相比，UGF-SORA算法效率较低，但优化结果的相对误差远远小于HL-RF算法，显然所提算法具有较高计算精度。

4.3 算例3

该算例是功能函数为非线性的可靠性优化问题，有3个随机变量，并且其中一个变量服从非正态分布。其数学模型为

(25)

进行可靠性分析时，由于计算量庞大， 使用UGF法进行可靠性分析环节会选择引入合并同类项操作来提高效率，传统算法以及所提算法的优化结果在表4中列出。

表4 算例3不同算法优化结果对比Tab.4 Comparison of optimized results of different algorithms in Example 3

表4中数据表明，在使用合并同类项时，可靠性计算精度下降不会太多，在可接受范围内，并且两种方法优化结果对应的相对误差也较为接近，但优化效率得到极大提高。因此，使用UGF法进行可靠性分析时可考虑加入合并同类项操作来提高求解效率，该操作仅会带来精度上较小的损失。对比传统算法可以发现，所提算法具有良好的收敛性能以及较高的求解精度，但其存在优化效率低的问题。虽然合并同类项操作的引入在一定程度上提高了求解速度，但如何提升优化效率依旧是值得深入研究的话题。

5 结论

本文提出了一种结构可靠性优化的UGF-SORA方法，该算法从传统SORA方法的偏移向量出发，重新建立了SORA模型，引入UGF法进行可靠性分析和评估，并采用最小二乘法完成偏移向量的更新。通过数值算例分析，可得出如下结论：

1)相对于现有典型的基于HL-RF算法、AMV的双循环算法、SLA算法、SORA算法等，所提方法可以在保证一定优化效率的同时得到较高精度的优化解。

2)当实际问题随机变量为非正态，功能函数为高度非线性时，优化结果可能会出现精度低或不收敛等现象。基于UGF的结构可靠性分析方法不受随机变量和功能函数类型影响，所提方法为此类问题提供了新的求解策略。

3)成本和精度是一对相互制约的矛盾，在传统方法精度失控的情况下，通过增加可控的成本获得较高的精度，是理性而有效的措施。