《算法分析》教学方法探索

张本群

（兴义民族师范学院，兴义562400）

0 引言

问题的描述：求n 的欧拉函数，即为小于n 且与n互质的数的个数（包含1）。下面均用Euler（n）来表示n 的欧拉函数。

对于欧拉函数的求解，一种方法是直接讲最优算法；另一种方法是通过概念的描述，找出问题的本质，最后才写出最优算法。解决同一问题，用这两种不同的方法，在实践中对学生的接受程度和取得的效果进行分析比较。

1 直接讲解最优算法

在往届的授课时，讲欧拉函数的求解时都是直接讲最优化的方法，利用欧拉函数的性质：

对于一个正整数n 的素数幂分解n=p1q1×p2q2×p3q3×…×pkqk

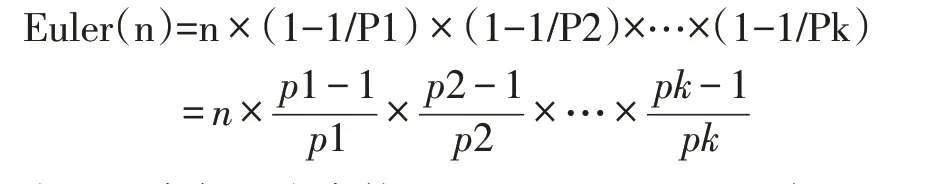
主要是求每一个素数因子p1，p2，…，pk，根据上面的公式，就可求出欧拉函数。

时间复杂度为ο(sqrt(n))。具体算法如下：

但用这种方法学生不易理解，计算公式和问题的描述相差甚远，学生是知其然不知其所以然。对于怎么来的欧拉函数的性质不理解，给出性质后，能写出算法，但如果不给性质，学生是写不出算法的，算法没有写出来，也就谈不上对算法的分析了。于是，在教学过各中调整了教学内容和方法，在这一学期的《算法分析与设计》中，先让学生理解问题的描述，分析问题的本质，最后再着手写最优的算法。

2 改进后的教学内容及方法

2.1 先理解概念

先根据问题的描述，理解概念，即直接用概念来解决问题（蛮力法）。

求n 的欧拉函数，就是小于n 且与n 互质的数的个数（包含1）。那么，赋欧拉函数初始值为1，对于小于n 的数i（i 从2 到n-1），逐个判定i 与n 有没有除1以外的其他因数，如果有，判定下一个，否则欧拉函数加1。

算法对小于n 的数i（i 从2 到n-1），判定i 与n 有没有除1 以外的其他因数，如果有，跳过这个数，如果没有，即i 与n 互质，与n 互质的数加1。最后函的的返回什就是欧拉函数的值。这样写学生很容易理解，完全根据概念来写算法，但该算法有很多重复的计算。例如，求Euler（10），已经判定2 是10 的因数了，那么只要是含有因数2 的数，都不会和10 互质。我们再判定4，6，8 是否为10 的因数，就显然是重复的计算，该算法的时间复杂度为O(n2)。明显有改进的空间。为了避免如此重复的计算，想到用类似于筛法求素数的方法，用筛法删去与n 不是互质的数，剩下的就是与n 互质的数了。

2.2 分析问题的本质

根据问题的描述，分析出欧拉函数Euler（n）本质特征。

如果n 是素数，根据素数的概念，n 没有除1 和它本身以外的其他因数，n 与i（i 从1 到n-1）都是互质的，由此得出性质1。

性质1：如果n 是素数，Euler（n）=n-1；

事实上，对于两个不同的素数p 和q，有Euler（pq）=Euler（p）×Euler（q）

对于1 到pq 间的数，因为p，q 不相同的素数，它们间的共同因数p 的倍数和q 的倍数，即p，2p，…，（q-1）p，qp 和q，2q，…，（p-1）q，pq。又因为pq 既是p 的倍数，又是q 的倍数，所以Euler（pq）=pq-p-q+1=（p-1）（q-1）=Euler（p）×Euler（q）

推广得出，对任意两个互为质数的m，n；均有Euler（mn）=Euler（n）×Euler（m）

证明：由m，n 均为素数可知m，n 无公因数，得出：

Euler（m）Euler（n）=m（1-1/p1）（1-1/p2）（1-1/p3）…（1-1/pk）·n（1-1/q1）（1-1/q2）（1-1/q3）…（1-1/qr），其中p1，p2，p3，…，pk 为m 的质因数，q1，q2，q3，…，qr 为n 的质因数，而m，n 无公因数，所以p1，p2，p3，…，pk，q1，q2，q3，…，qr 互不相同，所以p1，p2，p3，…，pk，q1，q2，q3，…，qr 均为mn 的质因数且为mn质因数的全集，所以Euler（mn）=mn（1-1/p1）（1-1/p2）（1-1/p3）…（1-1/pk）（1-1/q1）（1-1/q2）（1-1/q3）…（1-1/qr），所以Euler（mn）=Euler（m）Euler（n）。

即Euler（mn）=Euler（n）×Euler（m）

如果n 有一个素数因数p1，那么p1 的所有倍数将被岀除，也就是p1 的所有倍数都不会与n 互质，由此可推得下面的性质。

性质2：对于一个正整数n 的素数幂分解n=p1q1×p2q2×p3q3×…×pkqk

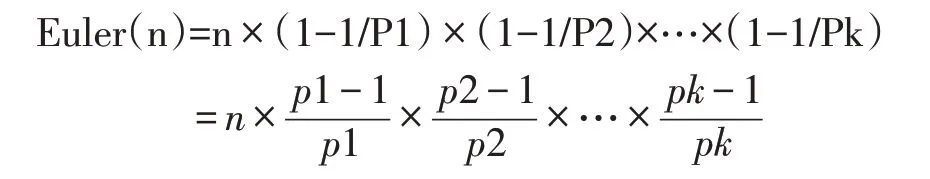
根据性质2，删除掉所有素数因数p1，p2，…，pk 的倍数，所剩的数的个数就是欧拉函数。类似于用筛法求素数的方法，用筛法求与n 互质的数。具体程序如下：

算法的时间复杂度为ο(nsqrt(n))。这一算法相对于根据概念逐个判定的方法有所改进，但仍然有可以再改进的地方。对于n 的每一个素数因数，我们都要遍历一次它的倍数，把该数换成0，筛选结束后又要遍历小于n 的每一个数组元素，不为0时才计数。

2.3 分析写出最优算法

事实上，求n 的欧拉函数只是求与n 与小于n 且与n 互质的个数，并没有要求求出哪些数与它互质，所以当找出n 的一个素数因数p 时，只需找出包含有因数p1 的数的个数即可，如果p1 是n 的一个素数因数，则有个n/p1 个数与n 有共同因数，故除去p1 的倍数后，还剩n-n/p1 个，以此类推，对于n 的全部互不相同的素数因数p1，p2，…，pk，欧拉函数

此算法在找出素数因数的同时就求出了欧拉函数。如72 的素数因数为2 和3，euler（72）=72×（1-1/2）（1-1/3）=24，最差的情况就是n 为素数时，需要搜索时间为ο(sqrt(n))。此算法的关键在于计算res=res/i*（i-1）时删除了i 的所有倍数，while（a%i==0）a/=i;展转相除后所得的a 不会包含因数i。

3 比较结果

对于n 的全部互不相同的素数因数p1，p2，…，pk，欧拉函数

这一描述中强调了三个问题，第一是全部，即不能是一部份，因数从2 到n 本身；第二是素数因数，如72＝8×9，不能用来求euler（72），原因是8 和9 虽然是72 的因数，但它们不是素数，故euler（72）＝72（1-1/8）（1-9）＝56 是错的，是素数不是因数也不行，例如5 是素数，但5 不是72 的因数，因此也不能算；第三是互不相同，如72=2×2×2×3×3，有3 个因数是2，2 个因数3，2和3 均为素数，但2 和3 都只能算一次，而不能算多次，所以在找到一个素数因数p 时，不是进行下一轮的循环，急于找下一个因数，而是辗转除去所有的因数p，得到的新数n 继续找素数因数。

如果直接根据性质2 来讲解，学生不易理解。通过概念，直接用蛮力求n 的欧拉函数，时间复杂度是ο(n2)，用筛法先将互质因数筛出来，再线性搜索出不为0 的结果，时间复杂度为ο(nsqrt(n))，而用改进后用筛法，找出素数因数的同时就再接算欧拉函数，同时除去所有含该因数的数，时间复杂度是ο(sqrt(n))；时间上得到了很大的提高，所以对同一个问题的求解，由于使用的算法不同，花费的时间完成不一样。显然，改进后的算法更有效。通过这一问题的讲解，让学生认识到解决问题前要先分析，找出问题的本质特征，再着手分析写出算法，写出更好的算法。这样逐步优化时间复杂度的教学方法，使学生体会到对算法分析的重要性，学生效果更好。