改进果蝇算法优化回声状态网络的旅游需求预测研究*
陈明扬,王 林,余晓晓
(华中科技大学管理学院,湖北 武汉 430074)
1 引言
21世纪以来,旅游业迎来了快速发展的黄金周期,旅游业收入占GDP的比重从2007年的4.05%上升至2017年的6.53%,人均出游次数与单次消费保持高速增长,旅游人数的增长对旅游城市和景点的管理提出了更高的要求。旅游需求水平的相关信息对于商业机构和政府决策部门来说非常重要[1],而旅游产品具有易逝性,其需求受到季节、假期、天气以及突发事件等多重因素的影响,提高预测精度是旅游需求预测问题的研究重点[2]。
诸多学者尝试使用不同模型来提高需求预测精度与时效性[3],通常可以分为因果关系模型、时间序列模型和人工智能模型3类。如黄先开等[4]通过搜索关键词建立多元线性回归函数预测日游客量;Chu[5]使用单一变量自回归滑动平均ARMA(AutoRegressive Moving Average)模型预测亚太地区9个国家的旅游需求;雷可为等[6]构建了自回归移动平均模型与BP神经网络的组合预测模型;Chen等[7]将支持向量回归SVR(Support Vector Regression)模型应用于旅游需求预测,并与自回归移动平均ARIMA(AutoRegressive Integrated Moving Average)模型等进行了对比;Palmer等[8]使用人工神经网络模型预测巴利阿里群岛的旅游需求;Zins等[9]采用基于神经网络的模糊时间序列模型作为预测模型,对SARS期间的旅游需求进行预测;陈荣等[10]提出了一种将季节支持向量回归模型与粒子群优化算法相结合的旅游流量预测SSVR-PSO(Seasonal Support Vector Regression Particle Swarm Optimization)模型,选取2008~2011年黄山景区月度数据集进行预测。相比前2类模型,人工智能模型在非线性拟合、自适应学习等方面表现出较大优势,但传统的人工神经网络存在训练过程复杂、耗时长等问题。因此,寻找高效和精确的新型神经网络方法成为热门研究方向。
Jaeger等[11]提出了回声状态神经网络ESN(Echo State Network)。与传统算法相比,回声状态网络训练过程简单、高效,在一般条件下可以无限逼近动态系统,被广泛应用于各类预测问题。雷苗等[12]使用ESN对移动通信流量进行预测;Maiorino等[13]利用ESN处理与太阳黑子某种特征值预测相关的时间序列问题。但是,ESN也存在着自身的不足和局限性,比如ESN的参数与连接权重随机设定,而训练过程中只调整输出层权重,容易陷入局部最优解。目前所采用的常见方法是多次构建网络选取最优输出时的ESN模型,或根据经验选取参数来构建模型[14 - 16]。对此,许多学者对ESN的结构进行优化。Shi 等[17]为ESN开发了几种新的储备池拓扑结构,并对办公楼的能源消耗进行预测。姚为等[18]提出了一种具有分叉结构的回声状态网络预测模型,提高了ESN的预测精度。也有学者使用启发式算法对ESN进行参数优化,获得了良好的实验效果,例如Irani等[19]用遗传算法优化前向反馈神经网络的初始权值和阈值,但目前此类研究相对较少。Pan[20]提出的果蝇优化算法FOA(Fruit fly Optimization Algorithm)具有复杂度低、计算速度快、求解能力强等优点,已在许多组合优化和连续优化领域得到应用,如库存问题[21]和调度问题[22]等。Li等[23]使用FOA优化人工神经网络ANN(Artificial Neural Network)模型的结构参数,Zeng等[24]使用FOA优化了SVR的惩罚参数和换算系数,均取得了良好的实验效果。FOA自身存在收敛精度低、容易陷入局部极值等缺点。对此,韩俊英等[25]提出了一种自适应变异果蝇优化算法,根据种群的适应度方差和当前最优值,在概率P下通过突变算子干扰复制,以继续优化;Xu[26]通过增加惯量来改变非线性递减特征以及个体与群体之间的关系,构建了改进的IFOA算法(Improved Fruit fly Optimization Algorithm)。
本文引入计算速度快、求解能力强的FOA算法优化ESN的关键参数,首先对标准FOA进行改进,提高了该算法的性能。接着与ESN相结合,构建一个两阶段组合预测模型AFOA-ESN(Adaptive Fruit fly Optimization Algorithm-Echo State Network),最后利用新模型解决旅游需求预测问题,获得了较高的预测精度。旅游行业市场空间巨大,如中国文化和旅游部统计信息显示,2018年国内旅游人数达55.39亿人次,入出境旅游总人数达2.91亿人次,全年旅游总收入5.97万亿元。因此,准确地预测旅游需求有利于提高旅游资产的运营效率,合理安排交通、住宿以及餐饮等相关产业的经营计划,为经营决策提供一定的科学依据,具有重要的现实意义。本文为ESN在旅游需求预测上的应用提供了研究新思路,为相关经济活动管理提供有益的管理借鉴,同时取得了预测方法上的创新。
2 果蝇优化算法及其改进
2.1 果蝇优化算法
果蝇优化算法(FOA)通过模拟果蝇觅食行为寻找目标函数最优解,属于一种较为新颖的启发式算法。FOA算法拥有很强的全局搜索能力和快速收敛性能,算法结构简单、运行效率高。FOA算法主要包括种群初始化、随机飞行、确定味道浓度判定值、确定味道浓度、位置标记5个步骤。FOA算法的逻辑结构如图1所示。

Figure 1 Logic structure of FOA图1 FOA算法逻辑结构
(1) 种群初始化。
首先对种群规模(Sizepop)、最大迭代次数(Maxgen)和搜索步长(S_length)进行定义,Xaxis和Yaxis代表随机赋予果蝇群体的初始位置坐标值。
(2) 随机飞行。
在初始位置赋予群体内的每只果蝇1个随机飞行的方向,并记录每只果蝇的位置信息Xi和Yi,果蝇群体将在搜索步长范围内进行气味搜索,位置更新公式如下所示:
Xi=Xaxis+S_length
(1)
Yi=Yaxis+S_length
(2)
(3) 计算味道浓度判定值Si。
部分函数中果蝇位置的横坐标和纵坐标不能表达果蝇位置,因此用距离函数Dist求倒数后的值作为获得的味道浓度判定值Si。
(3)
Si=1/Disti
(4)
(4) 确定味道浓度值Smell。
根据果蝇群体的味道浓度判定值,通过式(5)求得关于食物的味道浓度,通常假设味道浓度越高,果蝇距离食物越近。
Smelli=f(Si)
(5)
(5) 位置标记。
味道浓度值最大的位置将被选为果蝇群体共同飞向的位置,即下一迭代的起始位置。同时,如果当前迭代的最优值(bestSmell)好于之前的全局最优(bestSmell_global),则用当前迭代的bestSmell值更新bestSmell_global。
[bestSmell,bestindex]=max(Smelli)
(6)
bestSmell_global=bestSmell
(7)
Xaxis=X(bestindex)
(8)
Yaxis=Y(bestindex)
(9)
式(6)中bestindex表示最大味道浓度值位置的索引,bestSmell表示返回的当前迭代最优值;式(8)和式(9)为位置更新公式,X(bestindex)和Y(bestindex)表示返回的当前迭代最优值的位置。
FOA算法的迭代过程包括上述的(2)~(5),如果达到停止条件(即迭代次数累加达到最大迭代次数),则停止迭代,并提取当前bestSmell_global作为整个果蝇搜索过程中找到的最优解。
2.2 果蝇优化算法的改进
标准FOA算法中,种群规模与搜索步长固定,可能导致局部搜索能力不足和搜索效率较低等问题。因此,本文针对FOA算法进行了自适应改进,根据当前位置味道浓度值对种群规模和随机搜索步长进行调整。
(1) 引入可变随机搜索步长策略。
随机搜索步长StepLength的调整因子为函数的当前值与目标值之比,调整因子乘以标准搜索步长StepLength_Standard后的值为下一迭代最大搜索步长。随机步长的优势在于,当前局部最优解f(t)较差时可以增加果蝇步长,快速跳出该范围,当前局部最优解f(t)较好时可以缩小果蝇步长,增加该位置的局部搜索能力。本文中,f(t)为第t次迭代的平均绝对百分比误差值,f_target为目标平均绝对百分比误差值。
StepLength(t+1)=
(10)
(2) 引入可变果蝇种群规模策略。
种群规模的调整因子为函数的当前值与目标值之比,调整因子乘以标准种群规模Sizepop_standard后的值为下一迭代的种群规模Sizepop(t+1)。当前位置解较好的情况下,果蝇种群受到较高气味浓度的刺激,搜索果实的果蝇数量增加;相反,当前位置解较差的情况下,气味浓度值低,搜索果实的果蝇数量减少。该策略可增强果蝇种群在当前解较优的位置的搜索能力,解较差时在当前位置适当减弱搜索能力。
(11)
经过上述优化过程,AFOA算法可同时提高运算效率和寻优效果,AFOA算法的执行步骤如下所示:
(1) 初始化。设置果蝇种群规模(Sizepop)、标准最大搜索步长(StepLength_Standard)和最大迭代次数(Maxgen),确定信息果蝇的数量(Sizepop_Info)和最大搜索步长(StepLength_Info)。
(2) 确定初始位置与随机位置。赋予信息果蝇初始位置(Xaxis,Yaxis),根据当前迭代的种群规模和最大搜索步长(第1次迭代为标准种群规模和最大搜索步长),随机生成当前种群规模数量的随机位置Xi和Yi,其中,随机数Rand取值是[0,1]。
Xi=Xaxis+StepLength(t)*(Rand-0.5)
(12)
Yi=Yaxis+StepLength(t)*(Rand-0.5)
(13)
(3) 计算味道浓度值。部分函数中果蝇位置的横坐标和纵坐标不能表达果蝇位置,因此用距离函数求倒数后的值作为获得的味道浓度判定值Si。
(14)
Si=1/Disti
(15)
(4) 提取最佳味道浓度信息,包括种群最佳味道浓度和最佳味道浓度所在位置,并将本次迭代最优位置设置成下一迭代的初始位置。
Smelli=f(Si)
(16)
[bestSmell,bestindex]=max(Smelli)
(17)
Xaxis=X(bestindex)
(18)
Yaxis=Y(bestindex)
(19)
(5) 判断是否为全局最优解。如果当前迭代的最佳味道浓度值低于上一代全局最优解,则将当前迭代的最佳味道浓度值赋给全局最优,同时记录全局最优的位置Xbest和Ybest。
Xbest=X(bestindex)
(20)
Ybest=Y(bestindex)
(21)
bestSmell_global=bestSmell
(22)

Figure 2 Structure of ESN图2 ESN结构示意图
(6) 调整种群规模和搜索步长。根据当前迭代最优解,对下一迭代的种群规模Sizepop(t+1)和搜索步长StepLength(t+1)进行调整。
(23)
StepLength(t+1)=
(24)
(7) 终止条件判断。未达到初始设置的最大迭代次数(Maxgen)时,重复(2)~(6),每次使迭代计数t增加1。迭代停止时,输出全局最优解(bestSmell_global)和最优位置(Xbest和Ybest)。
3 改进果蝇优化算法优化ESN的组合预测模型
3.1 标准ESN模型
回声状态神经网络属于递归神经网络的一种,与传统人工神经网络相比,ESN的优势在于学习过程简单、收敛速度快、避免陷入局部最优、非线性处理能力强等。ESN在初始时刻随机生成1个储备池,构成动态、复杂的隐含层空间。在训练过程中,输入权重和储备池权重的值不发生变化,输出权重的大小通常根据ESN实际输出值与目标值之间的误差,通过最小二乘法等方法进行调整。
典型的ESN网络包含输入层、储备池和输出层。ESN的输入层(Input Layer)有K个节点,用于将输入信息转换为初始激活信号。隐含层(即储备池,Reservoir)中节点数为N,代表储备池中神经元的个数。输出层中有L个节点,负责将储备池内部信息转换为输出层信息。输入层、储备池和输出层的连接权重分别用Win、W和Wout表示,Wback代表输出层对储备池的反馈权重。网络结构示意如图2所示,其中实线为必要连接,虚线为可选择连接。
ESN因其复杂的内部连接结构,具有递归神经网络的非线性动力学特征。当前时刻的信息从输入层输入到储备池,结合储备池内各神经元上一时刻状态和输出层的反馈信息,通过一定的权重,共同构成神经元的输入信号,再通过激活函数将输入信号转化为新一轮的状态向量x(t+1),更新公式如式(25)所示:
x(t+1)=g(Win·u(t+1)+
W·x(t)+Wback·y(t))
(25)
其中,g代表激活函数,函数计算结果构成神经元的状态向量x(t+1)。x(t)表示储备池在上一步的状态,0时刻的状态向量x(0)可以随机生成。u(t)表示第t步时的输入向量,向量的长度取决于输入信息的维度。y(t)表示第t步的输出向量,y(t+1)表示下一步的输出向量,由下一步的输入向量u(t+1)、下一步的状态向量x(t+1)和当前步的输出向量y(t)共同决定。具体公式如下:
u(t)=[u1(t),u2(t),…,uK(t)]T
(26)
x(t)=[x1(t),x2(t),…,xN(t)]T
(27)
y(t)=[y1(t),y2(t),…,yL(t)]T
(28)
y(t+1)=fout(Wout·(u(t+1),x(t+1),y(t)))
(29)
其中,fout表示输出层的激励函数。
3.2 AFOA-ESN组合预测模型
本文将改进的FOA算法与ESN相结合构建了一个新的组合预测模型AFOA-ESN。先对标准FOA算法进行改进,引入自适应调整的种群数量和搜索步长,再将改进后的FOA算法AFOA与ESN相结合,通过AFOA优化ESN并获取其关键参数(包括谱半径SR、输入单元尺度IS和储备池规模N),FOA算法的适应值为训练集的预测误差。最后将优化后的参数输入ESN,形成最终的组合预测模型,通过测试数据集检验参数优化的效果。AFOA-ESN的执行步骤如下所示:
(1) 数据预处理。将数据输入到组合预测模型中,为了防止输入数据的大小对模型产生影响,通常要对输入数据进行归一化处理。
(2) 参数初始化。首先设定AFOA和ESN的基本参数,AFOA的基本参数包括标准种群规模、标准最大随机步长、最大迭代次数等;ESN网络的基本参数包括谱半径大小、输入节点数、输出节点数、稀疏程度等。
(3) ESN参数寻优。用果蝇的位置表示被优化的参数,味道浓度表示目标值(预测误差)。AFOA生成随机位置后,果蝇利用嗅觉判断该位置味道浓度的高低,进而决定果蝇种群下一次飞行方向。果蝇种群在迭代中不断改变搜索位置与搜索范围,实现参数寻优过程,达到最大迭代次数时停止飞行。
(4) ESN网络预测。根据迭代过程中标记的最优预测误差和最优位置,判断AFOA的优化效果,最终找出ESN的最佳参数和实际预测值。
4 基于AFOA-ESN预测模型的旅游需求预测
为了检验组合预测模型AFOA-ESN在旅游需求预测中的应用效果,本文选择了2组真实的旅游需求数据。第1组为2011年1月~2017年4月北京游客的月度人数,为国内游客人数与国外入境游客人数之和,数据来自风力数据库(http://www.wind.com.cn/),如图3所示;第2组为2011年3月~2017年11月海南过夜游客的月度数据,数据来自阳光海南旅游统计网站(http://www.visithainan.gov.cn/government/),如图4所示。这2组数据均有学者用来检验需求预测模型的效果[27,28],因此这些数据可用于AFOA-ESN预测效果的对比分析。

Figure 3 Trend of monthly Beijing tourist arrivals图3 北京游客人数(万人次)
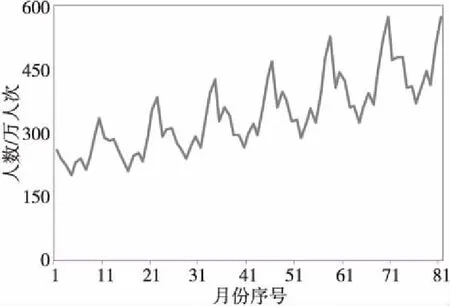
Figure 4 Trend of monthly Hainan overnight tourist arrivals图4 海南过夜游客人数(万人次)
本文综合运用多种误差评价指标,包括平均绝对误MAE(Mean Absolute Error)、平均平方差MSE(Mean Square Error)、方均根差RMSE(Root Mean Square Error)、归一化方均根差NRMSE(Normalized Root Mean Square Error)以及平均绝对百分比误差MAPE(Mean Absolute Percentage Error)5种,确保预测模型效果检验的全面性与客观性。
(30)
(31)
(32)
(33)
(34)

4.1 基于AFOA-ESN模型预测北京游客人数
4.1.1 实验数据与数据集划分
本组实验使用的数据共76个,分成训练集和测试集2个部分。和Sun等[27]的实验数据划分方法相同,并与文献[27]中基于互联网搜索指数(本文用到的是百度指数与谷歌指数)预测与无指数预测下的多种模型在相同数据集上进行比较,这些对比模型为多元时间序列分析ARIMAX(AutoRegressive Integrated Moving Average with Exogenous Variables)模型、人工神经网络(ANN)模型、支持向量回归(SVR)模型、最小二乘支持向量机LSSVR(Least Square Support Vector Regression)模型和基于多种核函数的核极限学习机KELM(Kernel Extreme Learning Machine)模型等。
本组实验训练集为2011年1月~2016年4月的月度数据,测试集为2016年5月~2017年4月的数据。本实验采用一步预测法,训练集中,用2012年5月~2015年4月的36个数据拟合2015年5月的旅游人数,2012年6月~2015年5月的36个数据拟合2015年6月的旅游人数,以此类推。AFOA从训练集中获取ESN的最优参数,作为测试集中ESN的参数,最后用2016年5月~2017年4月的12个数据的一步预测结果来计算平均预测误差,对比检验模型的预测效果。为了保持一致的测试条件,本组实验使用Lg(Q)函数对所有数据项进行预处理(Q表示月度游客人数,单位为万人次)。
4.1.2 参数设置与实验结果分析
实验在Python 3.7的编程环境下实现,硬件为2014年生产的Macbook Pro,操作系统为Mac OS High Sierra 10.13.3,处理器为2.8 GHz Intel Core i5,内存为8 GB 1 600 MHz DDR3。算法参数设置方面,依据专家推荐的经验[14,21,27,28]和多次实验,ESN输入层节点为36个,输出层节点为1个,储备池规模为50~500,谱半径大小为1.0~2.0,激活函数使用tanh函数,激活状态记忆参数a设置为0.20,在网络训练和测试过程中,除储备池规模和谱半径,其他参数保持不变;FOA算法种群规模为10,最大迭代次数为100,AFOA算法种群规模和搜索步长基于目标函数值自适应调整。文献[27]指出ANN、基于不同核函数的KELM模型采用试错法确定输入层和隐含层的神经元节点数,LSSVR和SVR模型采用高斯核函数、ARIMA模型采用最小化SC与AIC准则获取阶层、差分次数、阶数。因为文中并未给出具体的参数设置,故本文将FOA-ESN、AFOA-ESN得到的结果与文献[27]得到的最佳结果进行对比。
FOA-ESN具有良好的预测精度和优化效果,MAPE为0.53%,NMSE为0.67%,2项指标均为最优。同时,FOA-ESN模型具有很强的鲁棒性,每项数据的预测误差(MAPE)控制在1.59%以内。FOA-ESN能够使误差梯度快速下降,证明该模型能够有效解决旅游行业需求预测问题。
AFOA-ESN及对比模型的预测效果如图5和表1所示,数据显示AFOA-ESN的MAPE为0.41%,NMSE为0.67%,2项指标均为最优。表1中,KELM-lin、KELM-poly、KELM-rbf、KELM-wav分别表示基于线性核的、多项式核的、高斯径向量核的、小波核的KELM模型。
AFOA-ESN和FOA-ESN的迭代过程如图6所示。从图6中可以看出,AFOA-ESN在迭代过程中的收敛速度比FOA-ESN更快,预测精度有显著提升。
4.2 基于AFOA-ESN模型预测海南过夜游客人数
4.2.1 实验数据与数据集划分
本组实验选取2011年3月~2017年11月海南过夜游客人数月度数据,将数据集分为优化集、训练集和测试集3个部分,用于检验优化参数在预测效果上的稳定性。优化集用来得到拟合的输出权重,训练集通过AFOA优化集得到ESN的优化参数,并获取输出权重,测试集用于对比验证模型的预测精度。数据集划分方法和Li等[28]的实验保持一致,对比模型包括整合移动自回归(ARIMA)模型、向量自回归VAR(Vector AutoRegression)模型、主成分分析向量自回归(PCA-VAR)模型和主成分分析及自适应差分算法优化的后向神经网络PCA-ADE-BPNN(Principal Component Analysis-Adaptive Difference Algorithm-Back Propagation Neural Network),具体数据集划分如表2所示。

Table 1 Comparison of prediction accuracy among AFOA-ESN and other models表1 AFOA-ESN与其他模型预测精度对比

Figure 5 Experimental results of AFOA-ESN and FOA-ESN in Beijing tourist arrivals图5 AFOA-ESN和FOA-ESN的北京游客人数预测
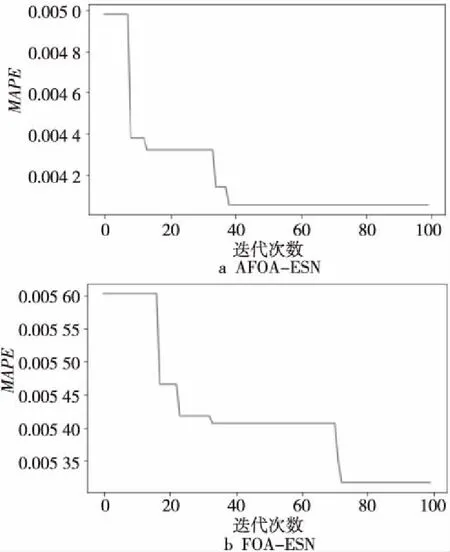
Figure 6 Iterative process of AFOA-ESN and FOA-ESN(Beijing)图6 AFOA-ESN和FOA-ESN的迭代过程(北京)

Table 2 Dataset partition of Hainan overnight tourist arrivals表2 海南过夜游客人数预测数据集划分
4.2.2 参数设置与实验结果分析
本组实验与第1组实验的参数设置基本保持一致(ESN输入层节点为12个,输出层节点为1),实验环境与第1组实验相同,各种参数设置如表3所示。

Table 3 Parameter settings of AFOA-ESN and other models表3 AFOA-ESN与其他模型参数设置
实验结果如表4和图7所示,数据显示AFOA-ESN的MAPE为1.56%,MSE为71.71,MAE为6.86,预测精度显著高于对比模型。

Table 4 Comparison of prediction accuracy among AFOA-ESN and other models表4 AFOA-ESN与其他模型预测精度对比

Figure 7 Experimental results of AFOA-ESN and FOA-ESN in Hainan overnight tourist arrivals图7 AFOA-ESN和FOA-ESN的海南过夜游客人数预测
AFOA-ESN和FOA-ESN的迭代过程如图8所示。从图8中可以看出,AFOA-ESN在收敛速度和预测精度方面均优于FOA-ESN,表明自适应因子的引入有效提高了FOA算法的寻优性能。

Figure 8 Iterative process of AFOA-ESN and FOA-ESN(Hainan)图8 AFOA-ESN和FOA-ESN的迭代过程(海南)
5 结束语
本文提出了一种改进FOA自适应能力的改进算法AFOA,提高了标准算法的运行效率,并与ESN结合构建了新的两阶段组合预测模型AFOA-ESN,拓展了算法的应用领域,为ESN的应用提供了新的思路。用AFOA-ESN对北京游客人数和海南过夜游客人数进行预测,在北京游客人数预测实验中,AFOA-ESN的MAPE为0.41%,NMSE为0.67%,2项指标优于ARIMAX、ANN、SVR、LSSVR和几种KELM的组合模型的。在海南过夜游客人数预测实验中,AFOA-ESN的MAPE为1.56%,MSE为71.71,MAE为6.86,在ARIMA、VAR、PCA-VAR、BPNN、PCA-BPNN和PCA-ADE-BPNN等模型中最佳。实验结果表明,FOA能够优化ESN的参数,提升预测精度,引入自适应因子的AFOA-ESN在收敛速度和预测精度上表现更优,验证了模型设计的有效性。将来可拓展寻优参数的数量,检验AFOA-ESN模型在多参数优化方面的表现,并尝试使用多种大数据手段(如网络搜索指数)丰富输入信息的多样性,更恰当地甄选适合旅游行业的预测信息。

