基于齿轮参数优化的减速器传动效率提高方法研究*
孙震震,李玉光,王淑芬,杨 铎,李富强
(大连大学 机械工程学院,辽宁 大连116622)
0 引 言
在减速器传动过程中,齿轮传动效率的高低直接影响着减速器的传动性能。目前,针对提高齿轮传动效率的优化有大量研究,如耿智博[1]通过对齿轮载荷谱分析,优化了齿轮模数和螺旋角,改善了振动性能;李玉龙[2]通过基于齿轮最佳摩擦学性能优选传动参数,提高了传动效率;宗长富[3]以齿轮宏观参数为变量,建立了降低振动和减小质量的目标函数,通过优化处理提高了传动效率;冯海生[4]研究了齿面摩擦对齿轮传动效率的影响关系;葛敏[5]通过对齿轮的微观修形,降低了齿轮振动与噪声,间接改善了传动性能;付学忠[6]将齿轮的承载接触分析与遗传算法相结合优化了小轮修形参数,减少了齿轮传动的振动与噪声;王春华[7]基于改进粒子群算法,以传动效率作为优化目标函数优化,改进了齿轮参数,提高了传动效率。
但是以上研究主要集中于固有齿轮上,对于立足于传动系统整体进行的齿轮研究较少。
本文以减速器作为整体,通过分别优化齿轮的宏观参数与微观参数,来减少齿轮啮合功率损失,提升减速器的传动效率;首先运用遗传算法对齿轮的宏观参数进行优化,以此为基础,运用KRIGING算法,拟合出齿轮的微观参数与齿轮啮合功率损失的关系,在保证精度的前提下运用EI准则寻找最优解,最终达到提升减速器传动效率的目的。
1 斜齿轮宏观参数变量的优化
本文以某一级减速器为例,如图1所示。

图1 一级减速器模型
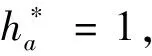
第一次优化目的主要是在降低齿轮体积的情况下,降低斜齿轮啮合功率损失,需要先建立两个优化目标函数,然后线性加权转换成一个新的优化目标函数。
一个优化目标是降低斜齿轮的啮合功率损失;另一个优化目标是在保证齿轮强度与耐久性的前提下,减轻齿轮的重量。
1.1 参数及范围的确定
本研究对斜齿轮较有独立性的结构参数,如模数mn、螺旋角β、压力角an、齿数z进行优化。其范围变化分别为:
2.5≤mn≤3.5,11°≤β≤13°,18°≤an≤25°。
1.2 目标函数
1.2.1 斜齿轮的啮合功率损失
斜齿轮的啮合功率损失主要由滑动摩擦功率损失和滚动摩擦功率损失组成,其中,滑动摩擦功率损失占主要部分[8],所以斜齿轮的滑动摩擦功率损失可为目标函数一。
由文献[9]可知,斜齿轮的滑动摩擦功率损失为:
(1)
(2)
(3)
式中:p—滑动摩擦功率损失;Fn—齿面法向载荷;f—啮合摩擦系数,此处混合状态下取0.04;mt—端面模数;i—齿轮传动比。
同时有:α≤ε∑。其中:ε∑—重合度;α—取小于等于ε∑的正整数。
1.2.2 斜齿轮的总体积
由立体几何知识可得,斜齿轮的总体积函数为:
(4)
为了使这两个目标函数相互关联,本研究通过加权的方式,使两个目标函数转化为一个目标函数。其加权系数W1、W2分别表示为:
(5)
(6)
式中:Pmin—单目标最小滑动摩擦功率损失;Vmin—单目标最小体积。
通过线性加权处理后,得到的优化目标为:
g=W1P+W2V
(7)
1.3 约束条件
(1)中心距约束:

(8)
(2)最小变位系数x约束:
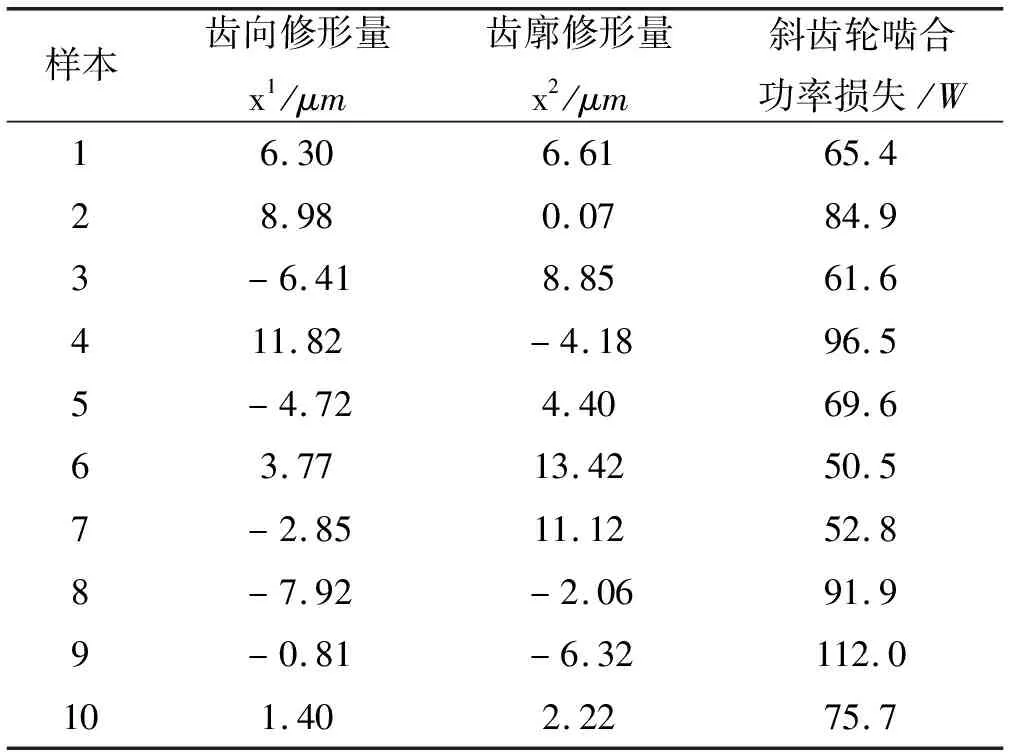
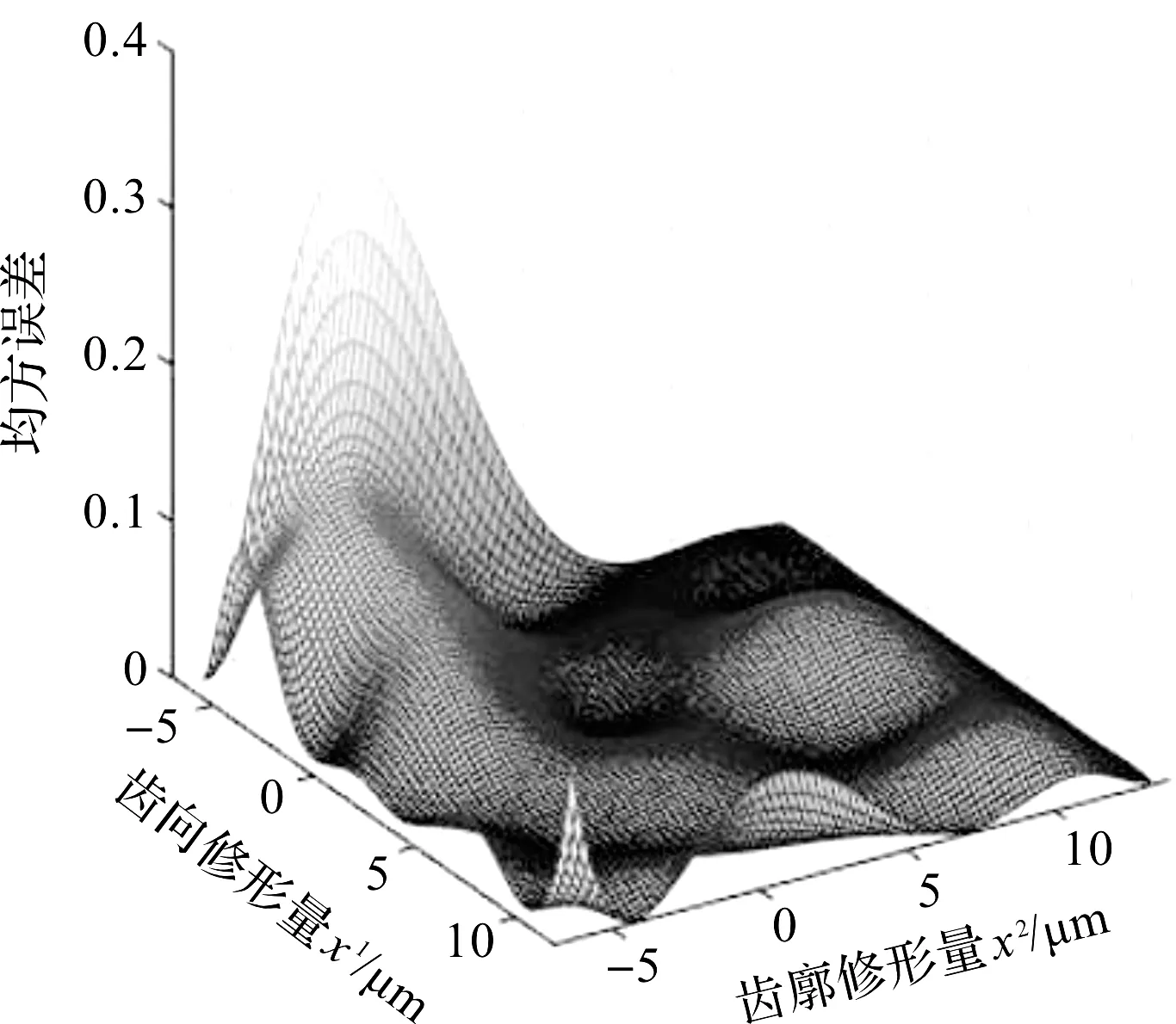
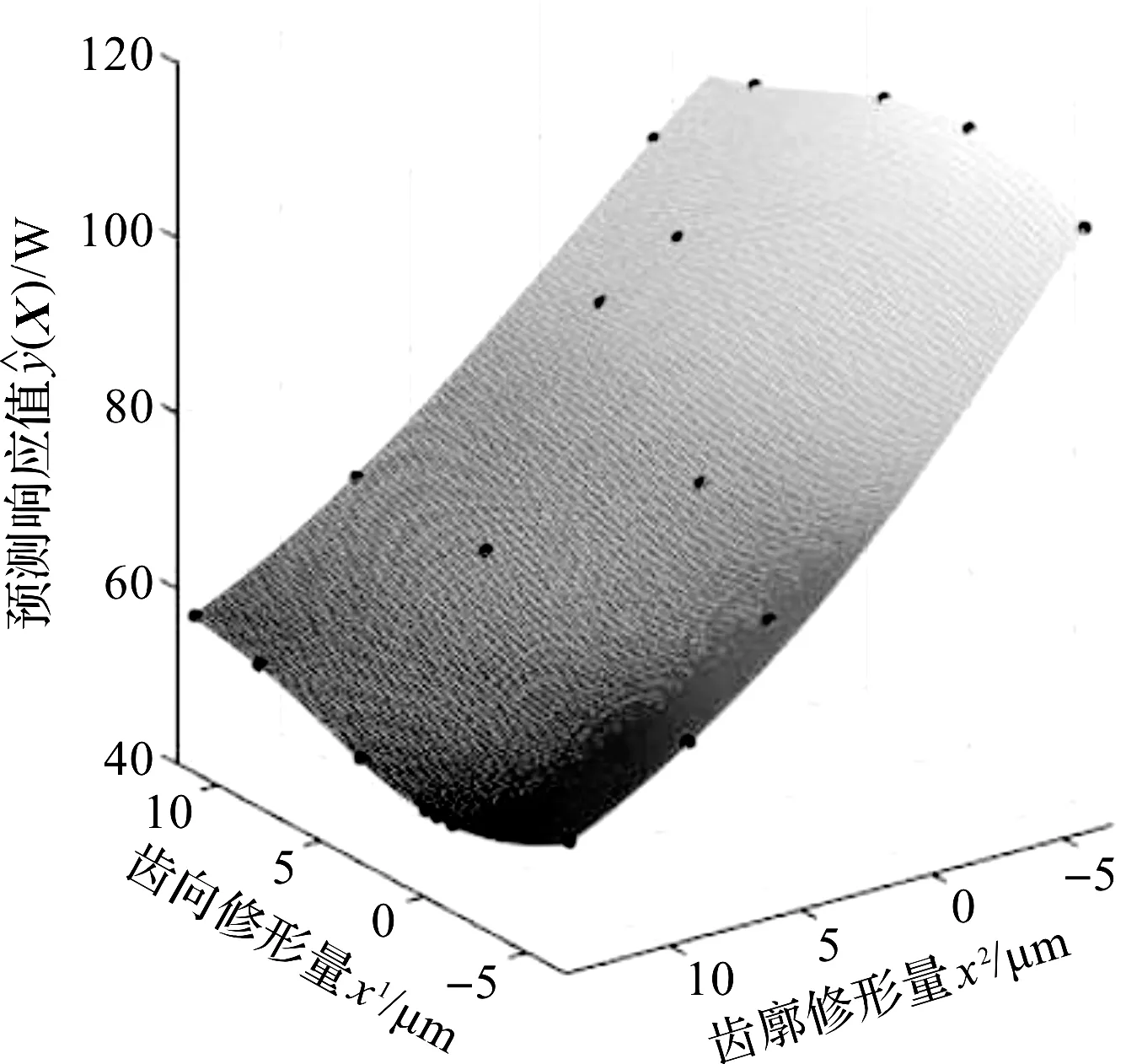
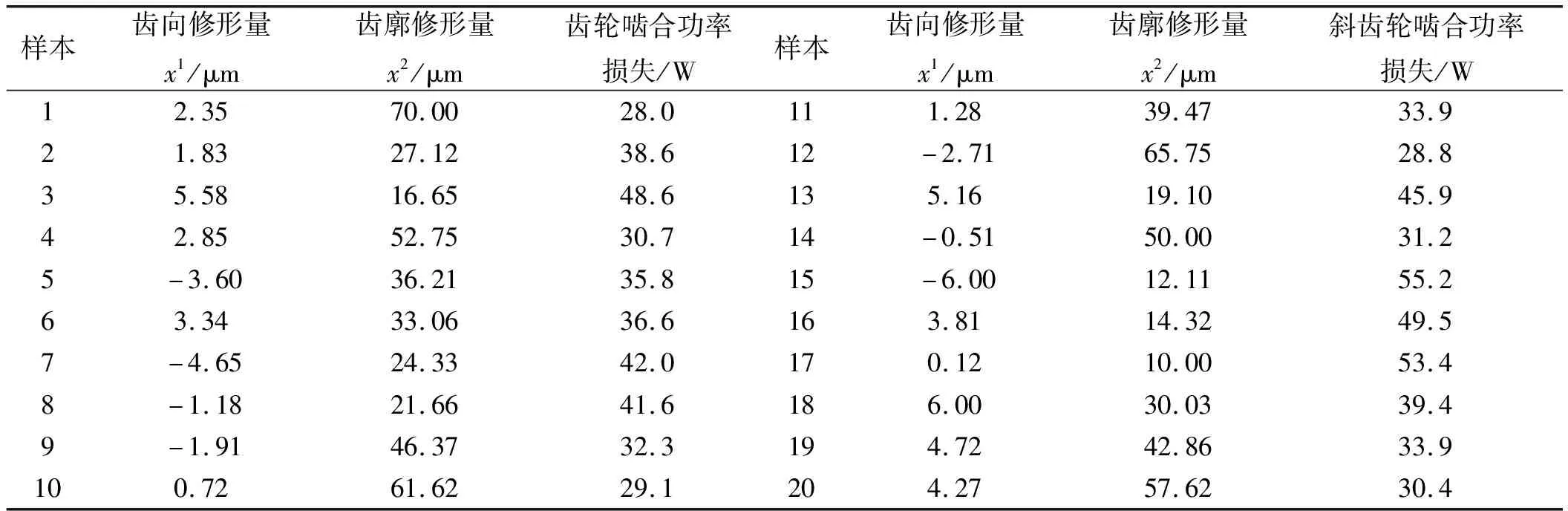
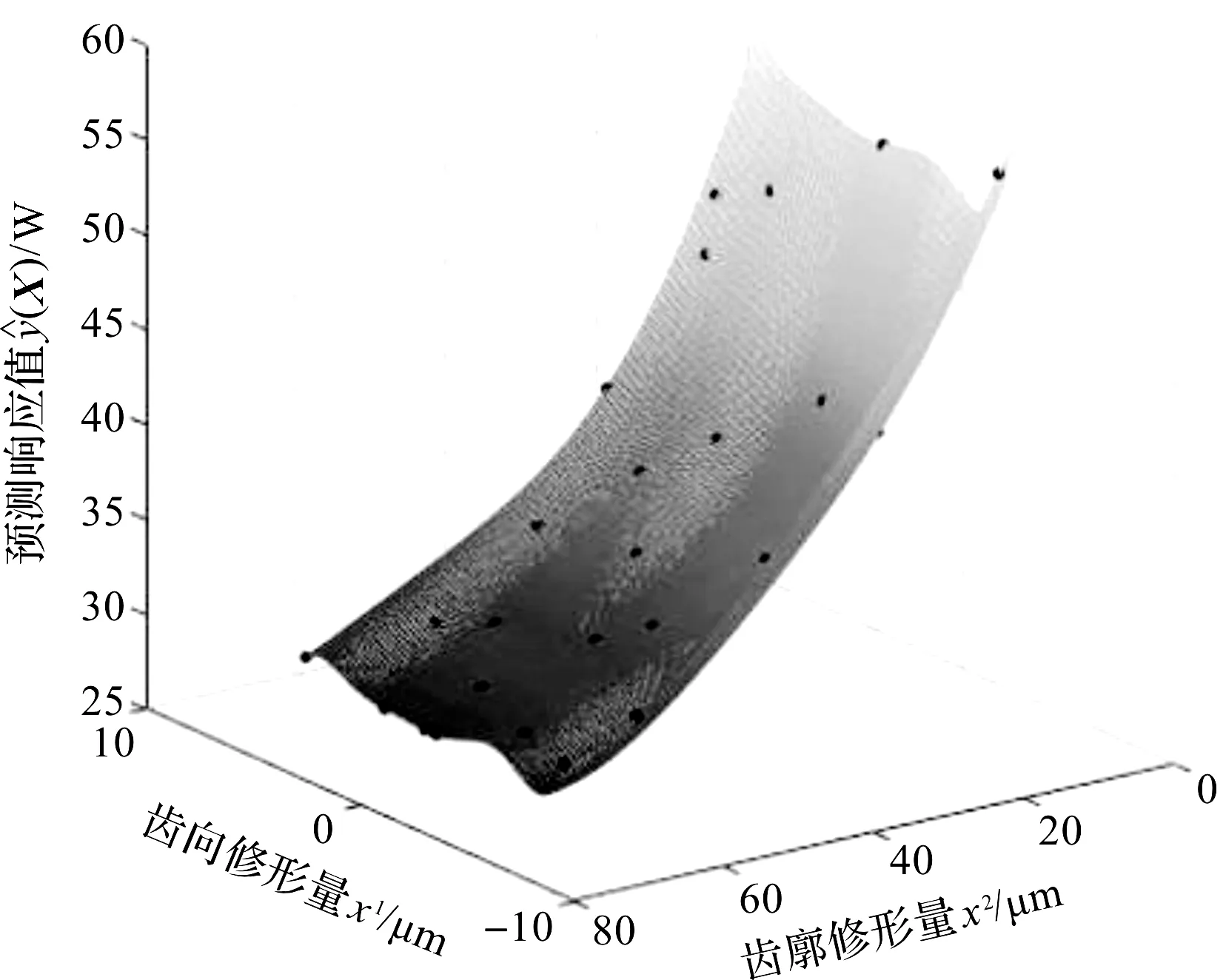
x (9) 式中:xmin—不发生根切时的最小变位系数。 齿轮速比约束为: (10) (3)重合度ε∑约束: εα+εβ≥ε∑ (11) 式中:εα—端面重合度;εβ—轴向重合度。 (4)强度与耐久性约束: 斜齿轮的失效形式主要为齿根断裂和齿面点蚀,需分别约束齿根弯曲强度与接触疲劳强度。根据文献[10],可计算出符合要求的参数。 遗传算法是计算机对生物系统进行模拟的一种算法,其通过交叉、变异、选择等选出最优解。本次优化通过遗传算法求解。 优化后斜齿轮宏观变量参数优化前后对比如表1所示。 表1 斜齿轮宏观变量参数优化前后对比 借助ROMAX软件,仿真数据显示斜齿轮啮合功率损失为85 W,降低了33.3%;同时,斜齿轮质量降低了0.058%,减速器的传动效率由98.4%提升到98.6%。 齿轮微观参数与齿轮啮合功率的损失之间是一种非线性关系,难以从理论上给出具体的解析式。为解决该问题,本文运用KRIGING算法,拟合齿轮微观参数对齿轮啮合功率的损失之间的关系,并求出最优解。 故笔者先运用均方误差(MSE)准则,来提高代理模型的精度,根据满足精度要求的代理模型,来判断齿轮微观参数对齿轮啮合功率的损失之间的关系,而后用期望改善(EI)准则来寻求最优解。 KRIGING是一种半参数化的拟合方法,包含参数化模型与非参数化模型,因此更具灵活性,可以通过已知信息来推导某点的未知信息。 给定m个参考点,其通式表达式为[11]: (12) 式中:X—单一样本点列向量;φ—线性回归系数;f(X)—响应的数学期望;z(X)—被视作随机过程的实现。 此处参数化模型部分选择二次函数模型,故有: (13) 式中:n—参数数量。 任意两样本点满足: cov[z(Xi),z(Xj)]=σ2R[R(Xi,Xj)],i,j=1,…,m (14) 式中:R(Xi,Xj)—任意两点间的空间相关函数。 相关函数模型常用的理论模型有3种,分别为:球形模型、高斯模型和指数模型。空间相关函数控制着KRIGING模型拟合的准确性,因为高斯模型可以描述高度连续的区域变量,且具有较好的精确性。 此处空间相关函数选择高斯模型,其通常表达式为: (15) 式中:θk—参数。 经拟合值的最小化误差均方差与无偏估计,拟合表达式可转换为目标函数: (16) 式中:rT(X)—含自变量的矩阵。 rT(X)={R(X,x1),R(X,x2),…,R(X,xn)} (17) (18) φ=(FTR-1F)-1FTR-1F (19) (20) (21) 式中:Y—样本点的响应值列阵。 预测点处均方误差(MSE)为: (22) 式中:u=FTR-1r-f。 EI是EGO(efficient global optimization)算法的核心,用来权衡局部搜索和全局搜索,但是往往忽略模型整体的精度,所以在运用MSE准则提高模型精度的前提下,运用EI准则对模型寻优。 记fmin=minY为当前样本点响应值的最小值,则任意点X处改善I为: (23) 期望改善EI为: (24) (25) 式中:φ(·)—标准正态分布的分布函数;σ(X)—点X处的预测值的标准差;φ(·)—标准正态分布概率密度函数[12]。 本文依据MSE准则,来提高DACE中KRIGING代理模型的精度;当MSE达到一定收敛条件时,再用EI准则来寻优得最优解。 其具体步骤为: Step1。通过拉丁超立方抽样方法在样本点空间选取初始样本,通常样本点数为变量维度的10倍; Step2。根据样本点及其响应值构建KRIGING模型; Step3。对不同维变量进行格网划分,并根据KRIGING模型预测格网划分后点的响应值; Step4。判断该模型预测点的max(MSE)是否满足要求。若不满足,则确定max(MSE)及对应点,记录该点并以该点及其响应值作为一个新的样本点,然后重复Step2;若满足要求,则进行EI收敛判断; Step5。若EI收敛,则输出最优解;若EI不收敛,则确定max(EI)及对应点,记录该点并以该点及其响应值作为一个新的样本点,然后重复Step2,直至达到收敛条件。 由式(1)可以看出,齿面接触情况影响着斜齿轮啮合功率。轮齿修形是改善齿面接触情况的一种措施,因此,可把齿向修形和齿廓修形确定为斜齿轮微观变量参数,齿向修形和齿廓修形均采用鼓形修形。 为简化优化过程,本次微观参数优化的对象为小齿轮轮齿修形。ROMAX软件仿真显示,优化后减速器斜齿轮的啮合错位峰值为1.95 μm,故初定齿轮齿向鼓形修形为1.95 μm。 齿廓鼓形修形量σa可由下列公式计算[13]: (26) 式中:ω1—单位长度载荷;Cy—平均啮合刚度。 通过计算可得σa为4.55 μm。以上述轮齿修形初定量为基准值,在其上下3倍标准差区间内寻优。 标准差公式可近似由下列公式计算: (27) 式中:Fp—齿距累积总公差。 (28) 式中:d—齿轮分度圆直径。 计算得σ=3.29 μm。 轮齿修形与斜齿轮啮合功率损失之间是一种非线性关系,理论上难以给出其解析表达。为了更好地解决此问题,本文运用KRIGING这一具有“统计性”的近似技术,来数值模拟轮齿修形与斜齿轮啮合功率损失之间的关系。故此处笔者以式(16)作为目标函数。 由上文可知: -7.92≤x2≤11.82,-6.32≤x2≤13.42 本次优化可简写为: s.t.-7.92≤x1≤11.82,-6.32≤x2≤13.42。 本文中轮齿修形参数为齿向修形与齿廓修形,故n=2。通过拉丁超立方抽样方法,选取10个样本点。精确度要求为:max(MSE)<1,max(EI)<10-6。 在Matlab上,本研究编写相应优化程序,然后根据样本点拟合模型。 选取的10个样本点及其对应的响应值如表2所示。 表2 样本点及其对应的响应值 经过10次迭代后结束,拟合出KRIGING模型预测点的均方误差如图2所示。 图2 KRIGING模型预测点的均方误差曲面图 由图2可知,在整个寻优区域内,KRIGING模型预测均方误差在0.5以下。 采用KRIGING模型,拟合出的轮齿修形与斜齿轮啮合功率损失之间关系如图3所示。 图3 轮齿修形与斜齿轮啮合功率损失之间关系拟合曲面图 由图3可知: (1)在一定的误差条件下,斜齿轮啮合功率损失在所取轮齿修形范围内,随齿廓鼓形修形量的增大而减小; (2)同一齿廓鼓形修形量下,齿向鼓形修形量越趋近与零,斜齿轮啮合功率损失越小; (3)斜齿轮拟合功率损失的响应值对齿廓修形的敏感度大于对齿向修形的敏感度。 根据式(16),以斜齿轮啮合功率损失最小为优化目标,在寻优区域内进行寻优,其结果为:x1=0 μm、x2=13.42 μm;此时,减速器传动效率为98.8%。 从图3还可知,轮齿修形与斜齿轮啮合功率损失之间的关系具有一定的趋势,所以为了得到更好地优化参数,可以对轮齿修形与斜齿轮啮合功率损失的关系再次进行拟合。 根据图3显示的轮齿修形与斜齿轮啮合功率损失之间的趋势,此次设定变量优化范围为:-6 μm≤x1≤6 μm、10 μm≤x2≤70 μm。 根据上述抽样方法,笔者抽取20样本点及其响应值如表3所示。 表3 样本点及其对应的响应值 再拟合精度要求和前次拟合中精度要求一样。经过5次迭代后结束,拟合出的轮齿修形与斜齿轮啮合功率损失之间关系如图4所示。 图4 轮齿修形与斜齿轮啮合功率损失之间关系的拟合图 由图4可知:轮齿修形量与斜齿轮啮合功率损失的关系和图3显示的一样,但预测值随着齿廓修形量的增大逐渐收敛。 接下来仍以斜齿轮啮合功率损失最小为优化目标,在寻优区域内进行寻优,其结果显示:x1=0.424 2 μm,x2=70 μm。 轮齿修形量如图5所示。 图5 轮齿修形曲面 此时,最优解为27.85 W。输入优化后的齿轮修形量,ROMAX仿真数据显示,齿轮啮合功率损失大小为27.9 W,与预测点处的误差仅为0.179%;减速器传动效率为98.9%,整体传动效率又提高了0.3%。 笔者运用遗传算法对齿轮的宏观参数进行优化,运用KRIGING算法,拟合出齿轮的微观参数与齿轮啮合功率损失的关系,在保证精度的前提下运用EI准则寻找最优解,减速器的传动效率提高了0.2%,斜齿轮的质量减轻了0.056%。 本研究利用KRIGING算法,及MSE和EI增点准则拟合轮齿修形参数与斜齿轮啮合功率损失之间的关系,并进行了微观参数寻优,得到了最优结果,减速器的传动效率又提升了0.3%。 经两次优化后,减速器传动效率由98.4%提升至98.9%,总共提升了0.5%,验证了这种优化方法的可行性;同时,该方法可为以后全面提升减速器的传动效率作参考。1.4 优化方法及结果

2 KRIGING模型及增点准则
2.1 KRIGING模型的基本原理
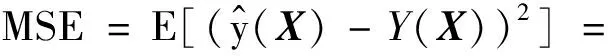
2.2 EI准则
2.3 模型优化寻优流程
3 斜齿轮微观参数的优化
3.1 变量及范围的确定
3.2 目标函数
3.3 约束条件
3.4 优化方法及结果
4 结束语

