汽车悬架系统的时滞反馈控制及其参数优化研究*
刘建均,孙艺瑕,李 胜
(上海工程技术大学 机械与汽车工程学院 上海 201620)
0 引 言
汽车悬架系统的隔振效果是影响汽车乘坐舒适性和安全性的关键因素。虽然传统的被动悬架系统具有结构简单和成本小等优点,但一经加工成型,结构参数便不可调整,从而无法更好地适应复杂多变的实际路况。
近年来,国内外学者对主动和半主动汽车悬架系统展开了大量的研究[1-4]。然而,由于信号的采集传输和控制力的计算等因素,主动汽车悬架系统中不可避免地存在时滞。时滞对汽车悬架系统控制的影响很大,可能会导致隔振效果下降,甚至失稳[5]。目前,对含时滞的汽车主动悬架系统的研究,主要是利用时滞补偿技术减少或抵消时滞带来的影响[6-8]。随着研究的深入,有研究发现,在汽车悬架的控制系统中适当地引入时滞,不仅可以改善悬架系统的隔振效果,还可以提高系统的稳定性[9-12]。由此,时滞被当作汽车悬架控制系统中可调的控制参数,为实现更好的悬架系统性能,获取最优的控制参数就尤为关键。
鉴于此,本文将在被动汽车悬架系统中引入时滞加速度反馈控制,以时滞和反馈增益系数为优化参数,采用粒子群优化算法,得到两参数的最优值,来提高汽车悬架系统的隔振性能。
1 汽车悬架系统的力学模型
时滞加速度反馈控制下,1/4汽车悬架系统的力学模型如图1所示。
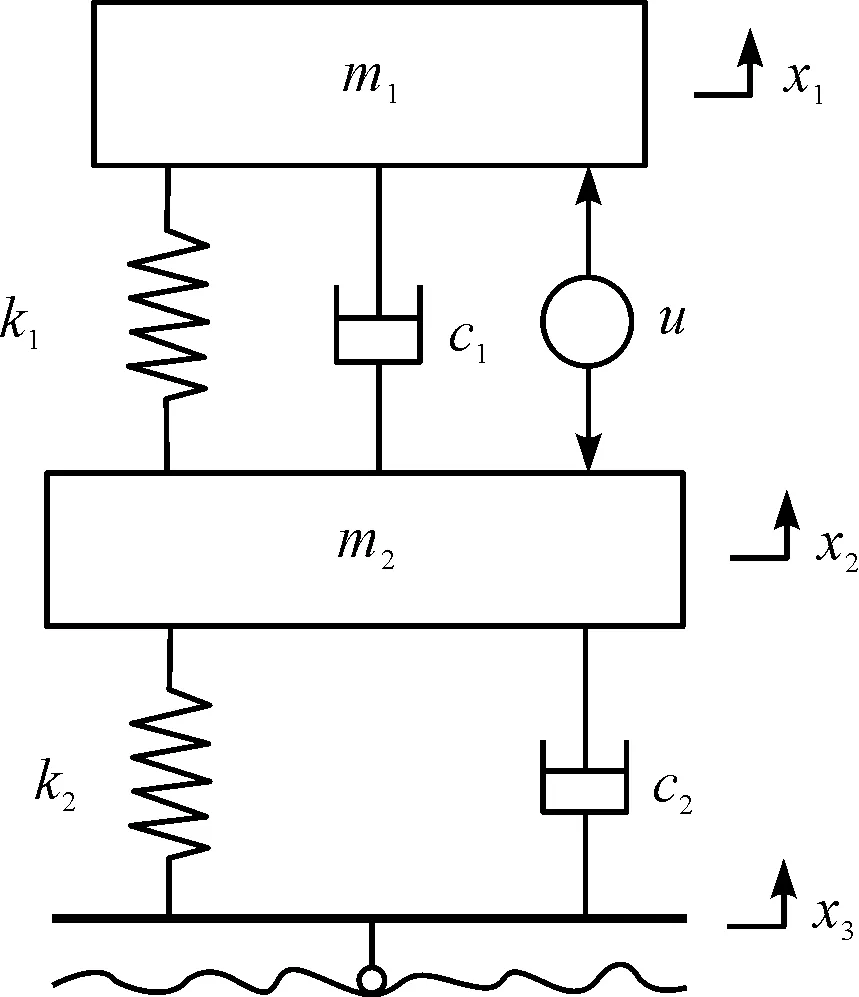
图1 力学模型
根据图1的力学模型,由牛顿第二定律可得到系统的运动微分方程:
(1)
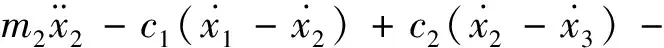
(2)
式中:m1—悬架质量;c1—减振器阻尼;k1—弹簧的刚度;u—时滞反馈控制力;m2—非悬架质量;c2—轮胎阻尼;k2—轮胎刚度;x1—车身的位移;x2—车轮的位移;x3—路面激励。
时滞反馈控制力u和路面激励x3[13]的表达式为:
(3)
x3=rsin(ωt)
(4)
式中:g—反馈增益系数;τ—时滞;r—路面激励幅值;ω—路面激励频率。
当g=0时,时滞反馈控制下的1/4主动汽车悬架系统退化为被动汽车悬架系统。
设式(1,2)的解为:
x1=a1sin(ωt)+b1cos(ωt)
(5)
x2=a2sin(ωt)+b2cos(ωt)
(6)
式中:a1,b1,a2,b2—待求系数。
将式(3~6)代入式(1,2),由等式左右两端sin(ωt)和cos(ωt)前面的系数相等,可以得到关于a1,b1,a2,b2的线性方程组:
[a1,b1,a2,b2]T=D-1E
(7)
其中:
D=(dyz)4×4,(y,z=1,2,3,4),d11=d22=k1-m1ω2-gω2cos(ωτ),d12=-d21=-c1ω-gω2sin(ωτ),d13=d24=-k1,d14=-d23=c1ω,d31=d42=-k1+gω2cos(ωτ),d32=-d41=c1ω+gω2sin(ωτ),d33=d44=k1,d34=-d43=-c1ω-c2ω,E=[0,0,k2r,c2rω]T。
由式(7)可得车身和车轮的加速度幅值:
(8)
(9)
2 稳定性分析及数值验证
2.1 稳定性分析
考虑到时滞反馈控制的引入,会给汽车悬架系统的稳定性带来很大影响,因此,本文对悬架系统进行稳定性分析。
设式(1,2)的特征根为s,由Laplace变换可得:
G(s)X(s)=F(s)
(10)
其中:
G(s)=
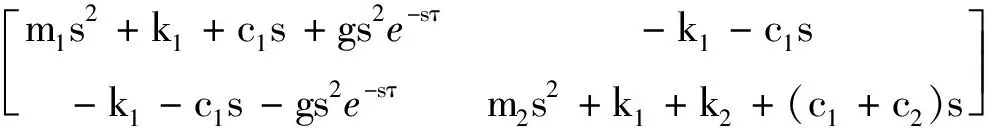
X(s)=[X1(s),X2(s)]T,F(s)=[0,F(s)]T。
时滞反馈控制下,汽车悬架系统的特征方程为|G(s)|=0,即:
P(s)+Q(s)e-sτ=0
(11)
其中:
P(s)=m1m1s4+(c1m1+c1m2+c2m1)s3+(c1c2+k1m1+k1m2+k2m1)s2+(c1k2+c2k1)s+k1k2,Q(s)=(-k2-c2s-m2s2)g。
当式(11)所有的特征根均具有负实部时,系统才稳定[14]。故先考虑系统的临界稳定状态,即所有特征根的实部皆为0。设s=ωci,(ωc>0),代入式(11),分离实部和虚部可得:
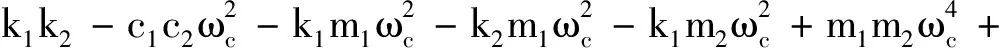
(12)
(13)
由式(12,13)可求得sin(ωcτ)和cos(ωcτ)的表达式。根据sin2(ωcτ)+cos2(ωcτ)=1,可得关于ωc的多项式方程为:
(14)
其中:
由式(14)可知,当反馈增益系数g取某一定值时,系数li(i=0,2,4,6,8)决定了方程根的取值情况,本文定义式(14)的正实根个数为N。当N=0时,系统不发生稳定性切换,即τ取任意正实数时系统的稳定性不变。当N≠0时,系统有N个根{ωc1,ωc2,…,ωcN},且对于每个根ωcm(m=1,2…,N)都存在无穷多个τ值{τ1,τ2,…,τ∞}与之对应。当τ从τn-ε增加到τn+ε(0<ε<<1,n=1,2,…,∞),方程特征根实部变化情况可由以下方程确定[15]:
(15)
在τ穿过临界τn的过程中,如果RT=+1,特征方程不稳定特征根的数量增加2个;如果RT=-1,特征方程不稳定特征根的数量减少2个。依次将反馈增益系数g取不同值,重复上述分析过程,可得到反馈增益系数和时滞的两参数平面上系统的稳定性分区图,如图2所示(本文中,取系统的物理参数[16]如下:m1=600 kg,m2=60 kg,k1=18 000 N/m,k2=200 000 N/m,c1=2 500 Ns/m,c2=1 000 Ns/m)。
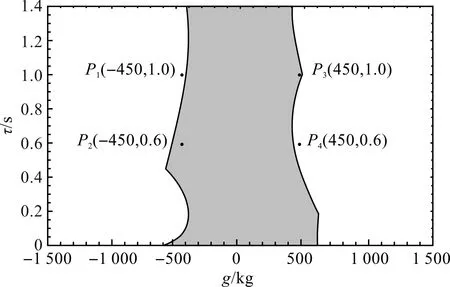
图2 稳定性分区图
从图2可以看出:当反馈增益系数和时滞的取值位于灰色区域时,系统稳定;当反馈增益系数和时滞的取值位于空白区域时,系统失稳。
2.2 数值验证
为了验证稳定性分析的正确性,本文选取4个点(如图2所示)。其中,点P2和P3对应稳定的系统响应,点P1和P4对应不稳定的系统响应。
分别将4个点的坐标代入式(1,2),同时取r=0.01 m,Ω=5.5 Hz(Ω=ω/2π),利用龙格库塔法进行数值仿真,可得到4个点对应的车身加速度时程响应,如图3所示。
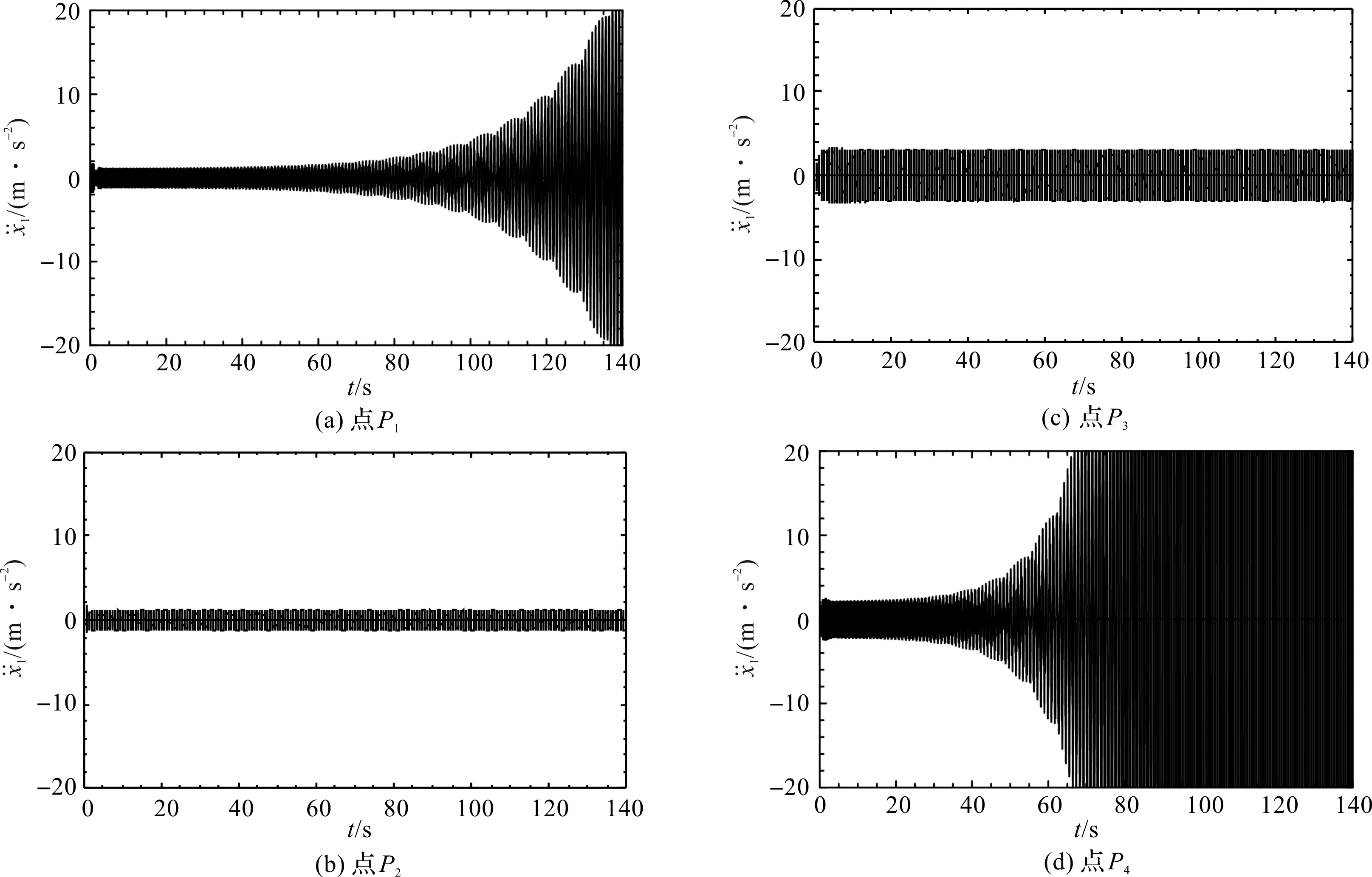
图3 车身的加速度时程响应
由图3可见:车身的加速度响应幅值收敛到某一定值,此时系统稳定;车身的加速度响应幅值发散,此时系统失稳。这与图2中P1-P4点对应的稳定性一致,从而证明图2稳定性分区图的正确性。
3 单频率处的控制参数优化及验证
3.1 控制参数优化
本文采用粒子群优化算法,对反馈增益系数和时滞进行优化求解。以车身的加速度幅值作为适应度函数,优化过程中相关参数的设置如下:粒子数为500,空间维数为2,最大迭代次数为1 000,学习因子为0.9,惯性权重为0.8,速度限制为[-1,1],位置限制为[-500,500]和[0,1.4]。
在频段1 Hz~20 Hz之间取离散频率点,本文对每个频率处车身的加速度幅值进行优化,并获得该点处最优反馈增益系数和时滞取值(gop和τop)。为了得到车身和车轮的加速度幅值的变化情况(增加或减少),定义ΦA和ΦB分别表示车身和车轮的加速度幅值变化的百分比,其表达式如下:
(16)
其中:X=A,B。
优化结果如表1所示。
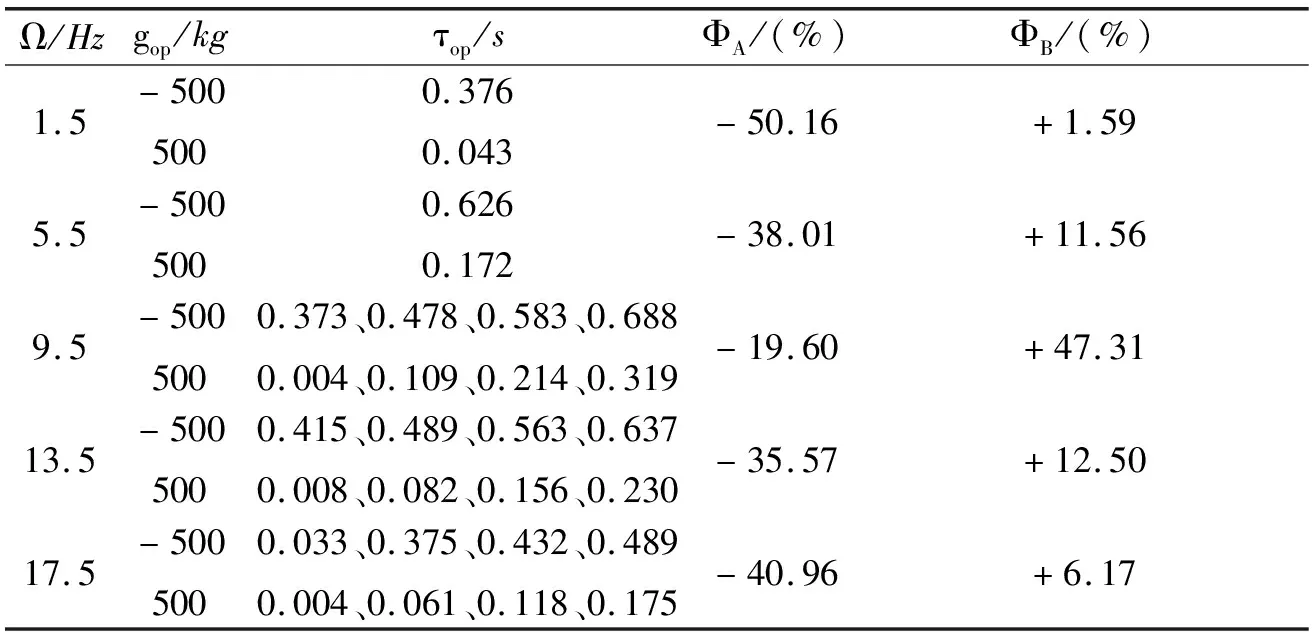
表1 优化结果
从表1可以看出:某些路面激励频率处存在多个最优时滞量,这给实际工程中时滞的取值提供一定的灵活性。
被动和最优时滞反馈控制下,车身和车轮的加速度幅值—频率关系曲线如图4所示。
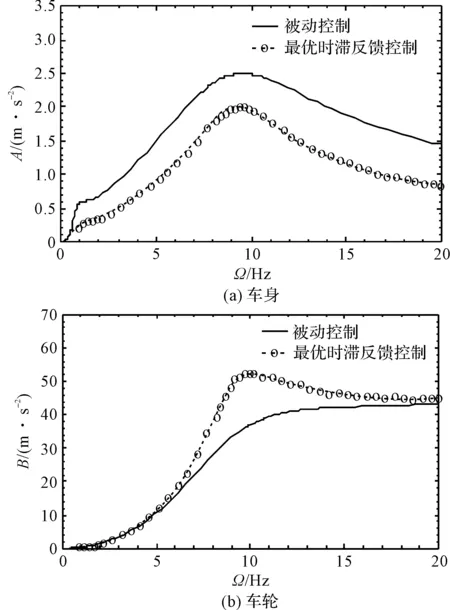
图4 加速度幅值-频率关系曲线
由表1和图4可知:与被动控制下车身的加速度幅值相比,最优时滞反馈控制下车身的加速度幅值得到一定程度的减小,表明汽车悬架系统的隔振效果得到改善。当Ω=1.5 Hz和Ω=9.5 Hz时,车身加速度幅值分别降低了54.05%和19.60%,而车轮加速度幅值分别增加了1.59%和47.31%,表明在时滞反馈控制下,汽车悬架系统的隔振效果得到了明显改善,且车身和车轮之间存在能量传递。
3.2 优化结果的验证
从表1中选取频率Ω=5.5 Hz和Ω=9.5 Hz,并对两频率处时滞反馈控制参数的最优结果进行验证。
通过数值仿真,分别得到两个频率处车身和车轮的加速度时程响应如图(5,6)所示。
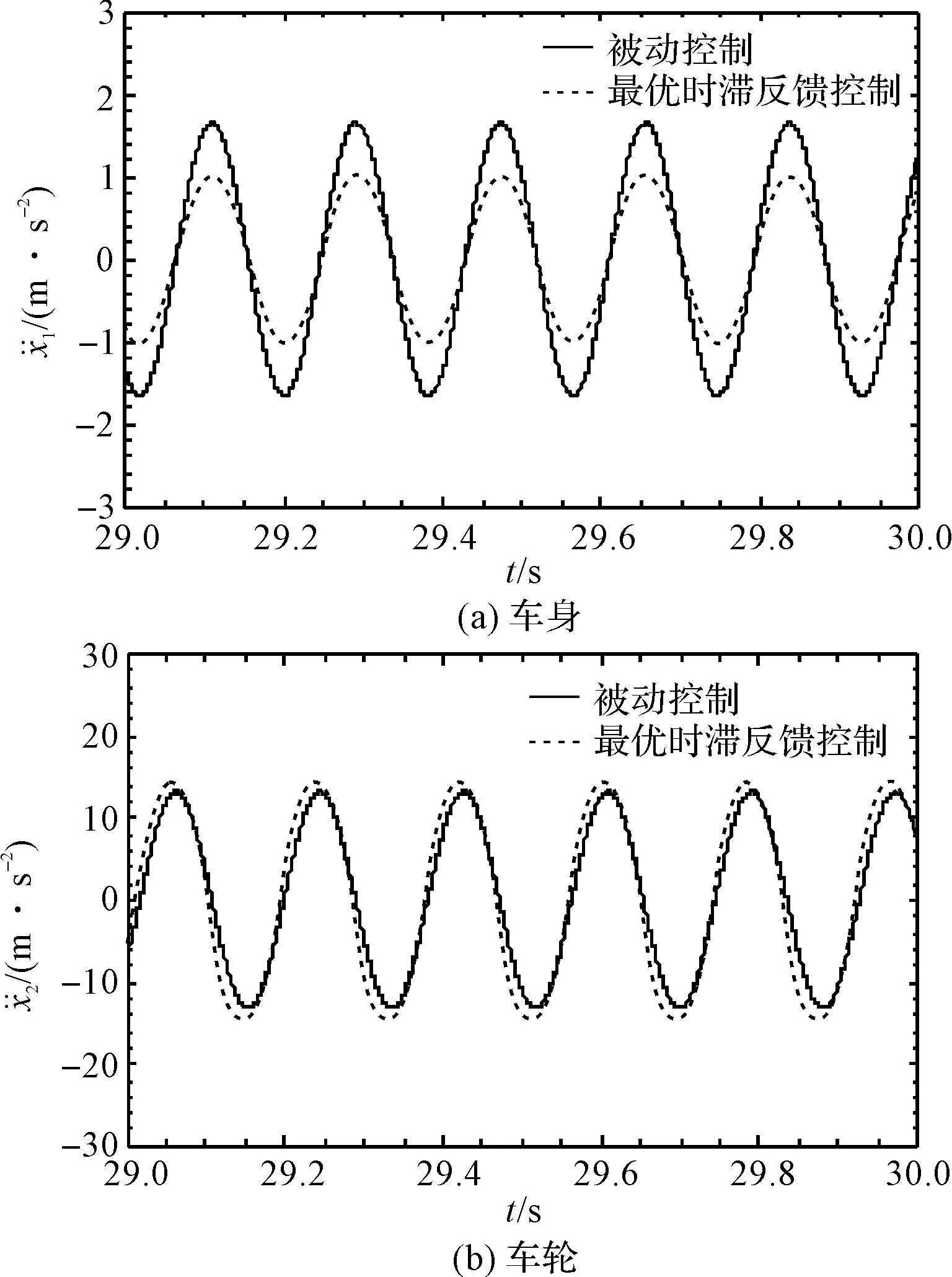
图5 当Ω=5.5 Hz时加速度时程响应
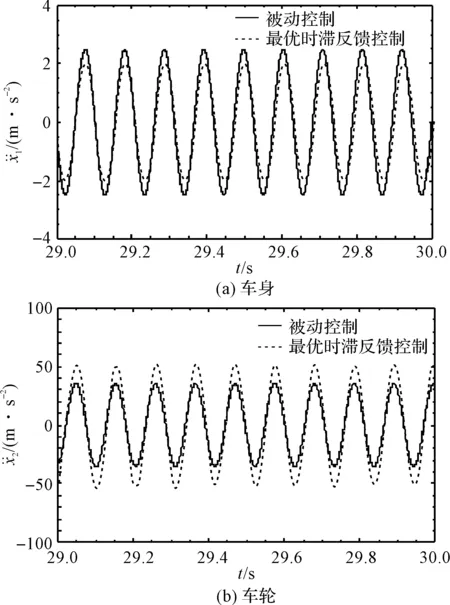
图6 当Ω=9.5 Hz时加速度时程响应
从图(5,6)可以看出:当Ω=5.5 Hz和Ω=9.5 Hz时,车身和车轮的加速度时程响应的幅值与表2中的优化结果是一致的,表明本文对控制参数的优化结果是可靠的。
4 结束语
本文采用了粒子群优化算法,研究了1/4汽车悬架系统中时滞反馈控制的参数优化问题。优化结果表明,在最优控制参数下汽车悬架系统的隔振效果得到了有效地改善,在频率1 Hz~20 Hz范围内车身的加速度幅值至少可降低19.60%;在某些频率下,存在多组反馈控制参数的最优值,这给实际工程中控制参数的灵活取值提供了理论参考。
在下一阶段,本研究将通过汽车悬架系统的实验研究,进一步验证最优时滞反馈控制下的汽车悬架系统的隔振效果。

