基于运算素养的三角函数题解法探究及延伸

叶墀龙

（福建省南安第一中学 福建南安 362300）

引言

在三角函数问题中，运用多种不同解题方法解决问题，提升学生数学运算能力，促使学生的数学核心素养形成。数学教育中，加强实践练习，提升学生数学解决问题能力，为学生运算素养形成打下基础。

一、函数与方程思想方法

函数作为高中数学教育的重点内容，与数学其他知识有着非常密切的关系，是学生解决问题的有效方法之一。通过函数思想的运用，可以将问题中数量关系以函数的方式表现出来，使问题变得更加清晰与直观。函数方程思想，就是利用函数知识，将问题构建方程，并利用函数关系解决问题，确定最终的答案[1]。该方法在三角函数解题中运用，巩固学生好函数基础知识，锻炼学生实践运用能力，促使学生数学运算素养形成。

例如，已知三角形的内角A、B、C的对边分别是a、b、c，已知asin（A+C）/2=bsinA，问题B为多少？

解，由 A+B+C＝π得(A+C)/2+B/2＝π/2，故 sin[(A+C)/2]＝cos(B/2)，①

另一方面，由正弦定理有a/sinA＝b/sinB，从而有 bsinA＝asinB，②

把①，②两式代入已知等式，asin[(A+C)/2]＝bsinA 得acos(B/2)＝asinB＝2asin(B/2)cos(B/2)，由 0＜B＜π得 0＜B/2＜π/2，从而可知cos(B/2)≠0，又显然a≠0，所以有1＝2sin(B/2)，sin(B/2)＝1/2，又因 0＜B/2＜π/2，所以 B/2＝π/6，所以 B＝π/3。

二、数形结合思想方法

数据与图像的结合，在三角函数解题中运用，提升学生问题分析与解决问题能力。课堂教学中，教师可以将数形结合思想运用在教育工作中，并引导学生利用此方法解决问题，使学生学会图像与数据之间的转换，以此提升学生问题分析效果，提升教育工作质量。

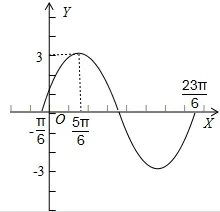
例如，已知函数y=3sin(1/2x-π/12)在长度为一个周期的闭区间上的图像，请画出图像，并探究x为多少时，函数有最大值。

当看到这一问题时，可以利用教材中 描述的五点法进行绘图，如下图，然后根据图像确定f（x）的最大值。当x=4kπ+5π/6（k∈Z），函数的最大值为3。

三、分类讨论思想方法

该思想方法，就是将解题过程分成解几个不同的类型，然后分开讨论。该方法在三角函数中运用，可以避免出现条件遗漏的情况，能够保证解题的准确性与有效性[2]。课堂教学中，将改思想方法的使用步骤渗透给学生，并为学生创建实践的机会，让学生在实践操作中积累经验总结解题方法，以此提高运算的效率，提高解题效果。

如，求方程6πsinx=x的解的个数

解：在解这一问题时，需要明确问题的核心，了解出题意图。通过对题干的分析，发现此问题的意图就是求函数f(x)=sinx和g(x)=x/6π的图像交点个数。因为f(x)和g(x)都是奇函数，所以关于原点对称且过原点，只看一半就可以。①当x＞6π时，f(x)＞1，因此g(x)≤1，即在(6π，+∞)上没有交点。②当x=6π时f(x)=1，g(x)=0，没有交点。③当x＜6π时，f(x)可以且只能取到(0，1)上的任何值。故在(π/2，π)、(2π，5π/2)、(5π/2，3π)、(4π，9π/2)、(9π/2，5π)上分别有一个交点，一共5个，所以在(-6π，0)上也有5个。还有原点。通过上述分析，可知一共6πsinx=x一共有11个解。

四、转化思想方法的运用

转化思想是高中数学三角函数解题中经常使用的手段，在运用的过程中，可以将多角问题转化成单角问题，将多个函数名称转化成一种函数名称，将未知角转化成已知角等等，通过问题的转化，理清学生的解题思路，使学生快速掌握运算方法与技巧，提高解题的准确率[3]。

例如，已知向量m=(sinwx，coswx)，n=(coswx，coswx)，(w＞0)若函数f(x)=mn-1/2的最小正周期是4兀。求函数取最值时的取值集合。

解决该问题时，可以采用转化方法，将复杂的问题简单化，然后运用基础知识解决问题。如f（x）=向量mn-1/2=sinwxcoswx+（coswx）2-1/2=1/2sin2wx+1/2cos2wx=√2/2 sin(2wx+π/4)。因为最小正周期是4兀，最小正周期是4兀，w=1/4，f（x）=√2/2sin(1/2x+π/4)。当sin(1/2x+π/4)=-1取得最小值-√2/2，此时1/2x+π/4=-π/2+2kπ，x=-3π/2+4kπ当sin(1/2x+π/4)=1取得最大值√2/2，此时1/2x+π/4=π/2+2kπ。x=π/2+4kπ。

五、结束语

总而言之，在高中数学三角函数解题中，不同思想方法的运用，优化学生解题思路，使学生掌握数学学习与解决问题方法。实际教学中，加强对各种解题方法的引入，鼓励学生自主总结学习经验，夯实学习基础，为运算素养形成打下良好的基础。