以案例为基础的参数与非参数回归教学辨析

朋文佳，朱玉，贾贤杰，芈静

科学研究的一个重要目的是评估结局变量与解释变量之间的数量依存关系，回归分析是达到该研究目的重要统计学分析方法。回归分析存在着重要价值，其一描述结局变量与解释变量之间的数量依存关系；其二通过解释变量预测结局变量；其三比较众多解释变量对结局变量影响大小[1]。现实世界中，结局变量与解释变量的数量依存关系错综复杂，为了更好地反映数量依存关系，回归分析理论在逐步完善，形成了参数回归分析和非参数回归分析[2]。在教学中发现学生对参数回归和非参数回归的理解和应用存在困难，本文以科研案例为基础，将参数回归分析和非参数回归分析的关键理论进行总结和辨析，并用R语言实现分析。

1 案例数据与分析目的

1992-1996年期间，美国开展了一项“脊柱骨密度”科学研究[3]，本文从该研究中截取了部分女性数据，见表1。数据集包含423位调查对象，3个变量。其中，变量id为调查对象编号；变量y是调查对象的脊柱骨密度含量，为结局变量；变量x是调查对象的年龄，为解释变量。本案例欲研究年龄对脊柱骨密度含量有无影响？如果存在影响，影响形式是什么？

表1 脊柱骨密度研究数据

2 参数回归及R语言实现

2.1 参数回归简介 因为脊柱骨密度含量是连续型定量变量，则解释变量年龄(x)与结局变量脊柱骨密度(y)之间的潜在趋势用参数回归形式描述为：

yi=f(xi) +εi,E(yi|xi)=f(xi)=β0+β1xi,E(εi)=0

其中函数f(xi) =β0+β1xi形式固定，β0和β1为待估计的未知参数，εi为随机误差，i=1,2,L,n为个体编号。因为f(xi) 是固定的函数形式，函数中未知参数有明确的统计含义，该分析方法被称为线性回归分析，是最简单的参数回归。β0和β1可以利用最小二乘法估计，即残差平和(SS)最小[4-5]：

线性回归要求数据满足“线性”、“独立”、“正态分布”和“方差齐”四个条件。线性回归中函数左边是y均数恒等变换，右边是x的线性表达式，所以在直角坐标系中数据点(x，y)呈现出“线性”；“独立”要求每个数据点相互独立；“正态分布”是指任意x取值下，y分布是正态分布；“方差齐”是指任意x取值下，y的方差保持不变。线性回归的要求限制了线性回归的使用，为了满足更多数据分析需求，将结局变量的分布扩展到指数分布族，形成了广义线性回归[6]。进行线性回归分析可以分为三阶段，其一绘制散点图，其二最小二乘法估计参数和统计推断，其三回归诊断。

2.2 参数回归R语言实现 绘制散点图(见图1)，可见随着年龄增长，脊柱骨密度含量上升，年龄前段脊柱骨密度含量增长多，年龄后段脊柱骨密度含量增长少。R语言是非常流行的统计分析语言。在R语言中完成线性回归的方法众多，本文为了扩展至广义线性回归分析，介绍glm()完成线性回归分析[7]，分析代码如下：

图1 年龄与脊柱骨密度散点图

spb<-read.csv("spina_bone.csv") #读入数据

lin_fit <-glm(y～x, family=gaussian(link = "identity"), data=spb) #设置线性回归

summary(lin_fit) #输出结果

spb$e<-lin_fit $residuals #保存残差，用于绘制残差图

主要分析结果见表2。

表2 脊柱骨密度研究数据线性回归分析结果

从分析结果可知，脊柱骨密度与年龄的数量关系为f(xi)=0.494329 + 0.027256xi。但是从残差图(图2)发现，残差与年龄存在一定非线性趋势，表明线性回归不能完全描述脊柱骨密度与年龄间数量关系，导致脊柱骨密度与年龄之间数量关系的欠拟合。

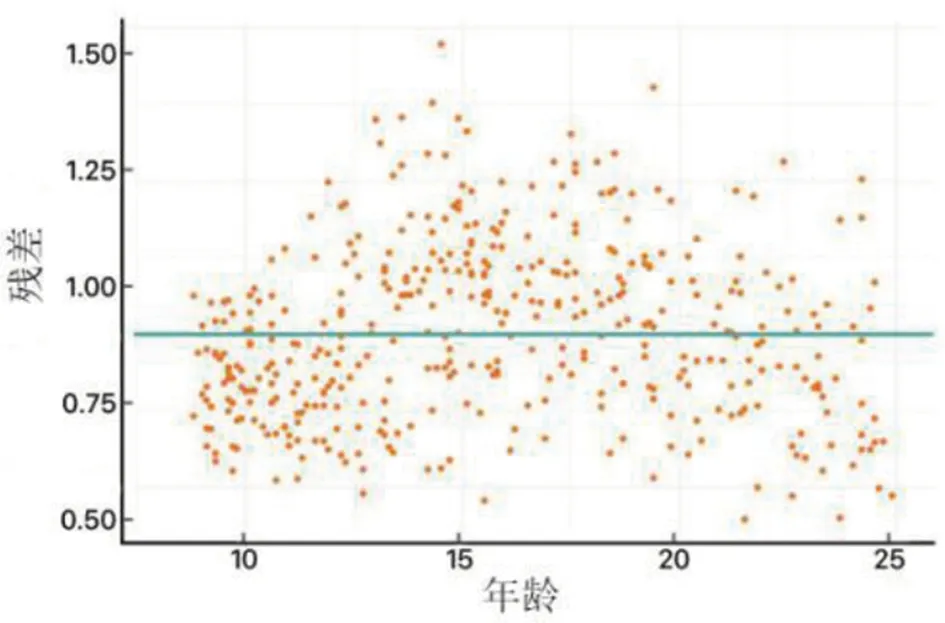
图2 年龄与脊柱骨密度线性回归残差图

3 非参数回归及R语言实现

3.1 非参数回归简介 上述描述发现脊柱骨密度与年龄之间数量关系不是线性，而是复杂的非线性关系，即不满足线性回归的“线性”要求，需要更为合适的分析方法。将两者之间的潜在趋势描述为：

yi=f(xi)+εiE(yi|xi)=f(xi)E(εi)=0

其中f(xi)没有固定形式，是需要通过数据估计的事先未指定的“光滑”函数，该分析方法被称为非参数回归分析。常见的非参数回归分析方法包含了局部平均、核光滑、局部多项式回归和样条光滑等[8-9]。非参数回归中结局变量不局限于高斯分布，可以像参数回归一样扩展到指数分布族。本文介绍基于样条光滑的非参数回归。

进行样条光滑的非参数回归需要对解释变量的变化范围按节点分为多个段，然后进行“基变换”[2,8,10]。当节点数过多时，导致过拟合现象。过拟合将数据的随机变异误以为是系统效应，掩盖真实的变化趋势[9]。为了控制非参数回归的过拟合现象，需要对光滑函数进行“惩罚”，即在残差平和中加入“惩罚项”，如下[2,8]：

式中λ(大于等于0)为光滑参数，通常通过交叉验证(cross-validation，CV)确定。当样本量较大时，交叉验证耗时长，可用广义交叉验证(generalized cross-validation，GCV)替代。

3.2 非参数回归的自由度 自由度是非参数回归模型复杂度的评价指标，等同于参数回归中自变量的数量(包含截距)或者自由度-1次多项式回归，自由度越大，表明模型越复杂，即解释变量与结局变量间关系越复杂。如果没有惩罚项，增加解释变量“基变换”的节点，相当于增加回归模型的自由度，会导致过拟合现象。加入“惩罚项”，是保留这些节点，但是限制影响力，相当于减少了回归模型的自由度。光滑参数和自由度之间存在单调的数学变换关系[2]。

3.3 非参数回归R语言实现 非参数回归的参数估计过程复杂、计算量大。在R中进行非参数回归的函数主要是gam()函数[3]，分析代码如下：

gam_fit<- gam(y～s(x, bs = "cr", k = 22), family=gaussian(link = "identity"), data = spb) #设置非参数回归，内部节点数量20

summary(gam_fit) #输出结果

spb$e<-gam_fit$residuals #保存残差，用于绘制残差图

anova(lin_fit, gam_fit, test = "F") #对非线性进行检验

主要分析结果见表3。

表3 脊柱骨密度研究数据非参数回归分析结果

从分析结果发现，截距估计值为0.929364；光滑函数对结局变量有影响，其自由度为5.604，表明年龄与脊柱骨密度间数量不是线性关系而是关系复杂的非线性关系；进一步对线性参数回归和非参数回归进行比较检验，发现两个回归模型存在差异，提示非参数回归更优(F=23.281，P<0.001)，进一步表明年龄与脊柱骨密度间之间不是简单线性关系，而是更为复杂的非线性关系。从非参数回归拟合图(图3)，发现17.5岁之前随着年龄增长脊柱骨密度增加，而17.5岁之后脊柱骨密度趋于稳定；从残差图(图4)，发现残差没有呈现额外趋势，表明非参数回归很好地反映了年龄与脊柱骨密度之间的数量关系。

图3 年龄与脊柱骨密度非参数回归拟合结果

图4 年龄与脊柱骨密度非参数回归残差图

4 讨论

通过上文阐述，发现参数回归与非参数回归有各自的优缺点。参数回归中函数部分有固定的表达式，函数中参数的估计简单且参数含义明确，但是参数回归函数形式呆板且对数据有着严格要求，难以精确拟合复杂的非线性关系，限制了其实际应用。非参数回归函数形式灵活多变没有固定的表达式，可以精确拟合复杂的非线性关系，但是回归参数估计复杂且意义模糊。用回归方法分析具体数据时，不能呆板套用方法，需要对数据进行精确地“诊断”，才能准确地分析数据，获得科学的结论。笔者推荐如下流程：先绘制散点图，拟合参数回归，拟合非参数回归，回归模型间比较，最后选择合适回归分析方法。

非参数回归需要控制过拟合现象。先设置节点，然后通过光滑参数或者自由度控制过拟合现象。在分析时，节点的数量和节点的位置都是需要解决的问题。相对来说，节点的位置对分析结果影响较小，为数据的等分点即可，节点的数量对分析结果影响较大。多数情况下，4个或5个节点就能满足应用需求了。大样本时，节点的数量为20～40[2,9]。相对于节点的数量和节点的位置，光滑参数与自由度对分析结果有着决定性的影响，建议用交叉验证或者广义交叉验证确定。为了满足更多科研需求，对参数回归与非参数回归取长补短，在可加模型假设下，将两者进行结合，一部分变量是参数回归形式，而另一部分是非参数回归形式进入模型，形成半参数回归[2-3,8]。半参数回归是当前流行的回归分析方法。