转化思想在高中数学解题中的应用例析

王白玉

(黑龙江省大庆市杜尔伯特第一中学 黑龙江大庆 166200)

转化思想是数学四大思想之一，贯穿于高中整个数学学习过程中。在实际解题过程中，一些看起来无从下手的题目只要通过转化思想便可以轻松解决[1]。在高中教学阶段中，我们应强化转化思想在教学中的渗透，让学生能正确掌握转化方法，以此提高他们的数学学习兴趣，拓展思维空间。

一、化陌生为熟悉

二、化繁为简

分析：该例题是融合诱导公式和二倍角公式的三角函数问题。如果直接对题目进行求解即使经过了复杂的计算过程也很难得到答案。但是，如果我们可以在解题过程中使用诱导公式和二倍角公式，将轻松得到答案。笔者在教学中发现，学生考试中这道问题的得分率不高，其主要原因就是他们缺少转化思想，没有意识到本题的简便计算方法。然而事实上，原函数可以简化为y=Asin（ωx+φ）+B，以此入手便可以轻松解决问题。

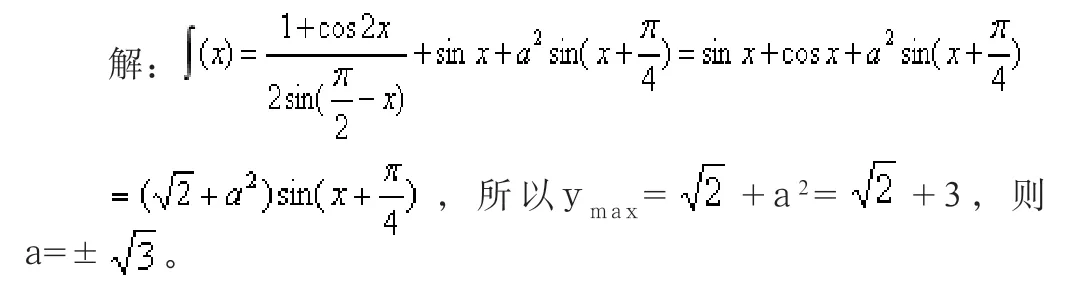
三、正难则反

正难则反是指在解题过程中如果顺着题目，从题目的正面思考问题遇到问题时，便可以从问题的反面入手去继续探索[3]。这种方法也是解题过程中常见的方法，主要考察的是学生的逆向思维。最典型的正难则反就是反证法，通过逆否等价来进行求证。在概率和排列组合中就经常会出现这一类的问题。

例3：A、B、C三人在进行射击游戏，如果三个人击中目标的概率都是0.6，求三个人各射击一次，至少一人命中的概率。

分析：如果从题目的正面入手，至少一人命中包括了三人中有一人命中、三人中有两人命中、三人中三人全部命中几种情况。解决这一问题就要分别计算几种情况可能会出现的概率。对于学生来说，这种分析方法相对比较繁琐，容易出现遗漏的情况。但是如果可以从反面分析，只要计算出对立事件，三人都没有击中的概率即可。

四、函数与方程互化

从近些年的高考试题中来看，函数与方程之间的相互转化是高考的热点之一，这就要求学生在解题中必须要掌握用方程思想来解决函数问题、用函数思想解决方程问题的方法。

（一）函数转化为方程

（二）方程转化为函数

例5：已知方程x2+x-k=0，在x∈[-2，2]上有实数解，求k的取值范围。

分析：这道题可以将方程问题转化为函数问题，即求函数k=x2+x的值域。

五、结束语

数学思想是数学的精髓，也是数学精神和数学理念中的重要组成部分。转化思想则是数学思想中的核心，想要帮助高中生建立起转化思想，必须经过长时间的培养和练习，做到潜移默化。本文简单分析了转化思想在高中数学中常见的几种应用方式，它们之间并不是孤立的，而是相互联系，可以进行融合应用。当然，转化思想也不仅仅包括以上几种表现形式，还包含数形结合、构造转化、等价转化等。在今后的教学中，笔者将继续对转化思想问题进行探究，并将其落实到教学工作中，希望可以帮助学生走出转化困境。