基于混合式BOPPPS教学法的贝叶斯公式教学设计

侯甜甜

(平顶山学院数学与统计学院 河南平顶山 467000）

《概率论与数理统计》是一门重要的专业基础课，课程具备系统的统计学知识、统计学理论、统计学的基本思想和方法，根据大量同类的随机现象的统计规律，对随机现象出现某一结果的可能性做出一种客观的科学判断，并对这种出现的可能性大小做出数量上的描述，比较这些可能性的大小，研究它们之间的联系，从而形成一套完整的数学理论和方法。

“全概率公式与贝叶斯公式”属于选用教材第一章第五节，位于使用教材的第24页至第27页，是在前一节“条件概率”概念提出的基础上，从已知简单事件的概率推算出未知复杂事件的概率的研究课题之一。为了计算复杂事件的概率，经常把一个复杂事件分解为若干个互不相容的简单事件的和，通过分别计算简单事件的概率，并利用概率的加法公式和乘法公式等得到最终的结果。在这类计算中，全概率公式起着重要的作用。而贝叶斯公式正好与全概率公式的作用相反，当一个事件已近发生了，要考虑该事件发生的各种原因的可能性的大小的时候，也就是当遇到“由果溯因”的推断问题，就需要用到贝叶斯公式了。可以说，全概率公式与贝叶斯公式是对第一章前四节内容的总结及综合应用。

传统的讲授法以教师为中心，教师讲授知识，学生只能被动接受，不能主动参与到课堂教学中，从而不能激起学生的学习激情，提高不了学生的学习兴趣，很容易造成课堂上大片的“低头族”。概率论与数理统计这种教学内容包含了大量统计思想的课程，若仅采用单一的、传统的讲授法进行教学，学生会不容易接受，也不能灵活应用。

混合式BOPPPS教学法以学生为中心，比较适应当代大学生的学习特点，因此，本文基于混合式BOPPPS教学模式，结合手机学习通互动平台，以“贝叶斯公式”为例进行教学设计。

一、混合式BOPPPS教学模式

随着现代信息技术和教育的深度融合[1][2]，从“互联网+教育”到“智能+教育”的发展，混合式教学在形式上表现为“线上+线下”以及传统教学和网络教学补充的教学方式，通过信息技术、借助慕课等教学平台，实现了线上新知识学习和线下知识内化的结合。内涵包括了教学空间、教学时间、教学方式、教学评价的混合。

“BOPPPS”教学模式源于加拿大技师技能培训[3][4]5]，以建构主义、交际法为理论依据设计的闭环式课程教学模型，主要包含6个环节，引入（Bridge-in）、教学目标（Objective）、前测（Pre-assessment）、参与式学习（Participatory Learning）、后测（Post-assessment）、总结（Summary）。各环节紧密结合，具备较强的可操作性。有助于实现课堂教学的体系化、条理化、合理化。

随着信息化技术的推广和普及[6][7]8]，开展线上网络教学和课堂教学相结合的混合式教学能够充分发挥教师的主导性和学生学习的主动性，从而提高教学质量。基于混合式BOPPPS教学模型的混合式教学模式，使学生利用课内外时间进行线上线下学习，做到以学生为中心。

二、基于BOPPPS教学法的贝叶斯公式教学设计

贝叶斯公式主要体现了由事件的先验概率，在某些既成事实的基础上，计算事件后验概率的思想，这种思想独树一帜，为后续的贝叶斯估计、贝叶斯判别做理论铺垫。根据BOPPPS教学模式，具体教学设计如下表所示：

表1 混合式BOPPPS教学模式在贝叶斯公式中的应用

（一）引入（Bridge-in）

导入作为第一环节，起着重要的作用，好的导入可以活跃课堂气氛，提高学生参与课堂的积极性。通过两个例子导入本课程。引例1：学校男生占60%，女生占40%，男生总是穿长裤，女生则一半穿长裤一半穿裙子，（1）随机选取一个学生，穿长裤的概率？（2）迎面走来一个穿长裤的学生但不知性别，求是女生的概率？引例2：（1）抛一枚硬币，正面向上的概率？（2）抛一枚硬币100次，正面朝上100次，反面朝上0次，问下一次正面向上的概率？

通过超星学习通平台发布这两个引例，让学生在手机端进行在线抢答，提高学习积极性和课堂的趣味性。

设计意图：1.用案例教学法和对比教学法，给出2个实际生活中的常见问题。让学生比较引例1和引例2的共同点。2.每个例子设计2小问，让学生利用已经学过的全概率公式计算第1问，并让学生体会第1问和第2问的区别和联系，启发学生第2问要用到贝叶斯公式，并启发学生思考如果没有学习贝叶斯公式，你能否计算出第2问呢？有没有一个大概的想法？和学生沟通交流，并让学生讨论，让学生说出自己的想法，为下一步给出贝叶斯公式做准备。

（二）学习目标（Objective）

知识目标：1.了解贝叶斯公式的背景、思想；2.掌握贝叶斯公式的计算步骤。

技能目标：1.将实际问题转化为概率统计问题的抽象思维能力；2.提高应用数学知识解决问题的意识。

情感目标：1.具备团队合作意识，能够独立思考；2.拥有爱国情怀和刻苦钻研精神。

（三）前测（Pre-assessment）

结合课程特点和学生学习心理特征、学习积极性等特征，通过超星学习通平台发布问题：什么是条件概率公式？什么是全概率公式？让学生在手机端进行在线抢答，提高学习积极性和课堂的趣味性。通过问题让学生回忆这两个公式，并为引出贝叶斯公式做准备。通过前测环节，了解学生的学习兴趣与能力，对教学内容的难易进行及时调整。

（四）参与式学习（Participatory Learning）

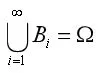
证明：

从几何概型解释贝叶斯公式：注1：事件A是结果，是已经发生的既成事实，事件B是导致A发生的原因。注2：要计算的条件概率违反正常的逻辑顺序，是已知结果求原因的倒推概率。注3：因果互换公式。

设计意图：采用讲授法，给出贝叶斯公式，采用讨论法，引导学生如何用之前学过的公式给出贝叶斯公式的证明，证明过程中的每一个等号分别用了什么公式。

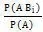
解：（1）记事件A为“穿长裤”，B1事件为“男生”，B2事件为“女生”，则全概率公式，

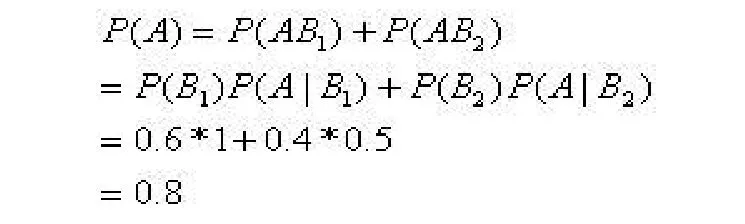
（2）贝叶斯公式，记A事件为“穿长裤”，B1事件为“男生”，B2事件为“女生”，则

（五）后测与总结（Summary）

在学习通发布测试创新和提高题目，《伊索寓言》中有个孩子与狼的故事，测试题目：现在用贝叶斯公式来分析，此寓言中村民对这个小孩的可信程度是如何下降的；课下探索作业，学习通完成。设计意图：采用讨论法，从几何概型角度解释贝叶斯公式，学生能更容易直观的理解贝叶斯公式，并采用这种办法让学生记住贝叶斯公式，能熟练运用，体会数形结合的重要性。列举孩子与狼的故事，让学生将具体问题抽象成概率统计问题，并用贝叶斯公式解决问题。通过案例分析得出的结论，启发学生做人要诚信。

图1 狼来了

思维导图的启发式总结，通过对课堂内容的小结，让学生对本节课的内容连贯化、系统化。观看学习通总结视频和相关论文。设计意图：经过上面教学活动，学生所获得的知识往往是零散的不完整的，让学生对本课的知识进行归纳小结，便于学生形成自己的数学体系，真正掌握本节课的知识。另外，教学中注重培养学生的反思能力，提高学生的学习效果。

三、结束语

经过探索与实践，采用混合式BOPPPS教学模式，提高了课堂教学效果和学生听课质量。同时，由于数学学科的性质，BOPPPS教学模式不一定适用于所有内容，怎样平衡线上教学时间和线下教学时间，是今后教学改革要继续探索的问题，我们也将继续努力，探索出更适合概率统计的具有学科特色的教学模式。