关于圆锥摆的推论及其应用

(江苏省海安高级中学,江苏 海安 226600)

1 圆锥摆ω2h=g的推导

如图1所示,在长为L的细绳下端拴一个质量为m的小球,绳子上端悬点固定,使小球在水平圆周上以恒定的角速度旋转,细绳所掠过的面为圆锥表面,这就是圆锥摆模型。

图1

设圆锥摆做圆周运动时圆心为O,圆心到悬点的距离为h,当圆锥摆做圆周运动的角速度为ω时,悬线与竖直方向的夹角为θ,小球受重力mg和绳子拉力FT作用。由图1可得沿半径指向圆心方向的合力为Fn=mgtanθ,又因为Fn=mω2r,r为圆锥摆做圆周运动的半径,由几何关系得：r=htanθ,所以：mgtanθ=mω2htanθ,整理得：ω2h=g。

可见,不管圆锥摆以多大的角速度ω做圆周运动,ω2与轨迹圆心到悬点的竖直高度h的乘积保持不变(等于重力加速度g),即ω2h=g,该乘积与悬线L的长短、悬线与竖直方向的夹角θ、摆球质量m无关。

2 圆锥摆ω2h=g推论的应用

2.1 比较两圆锥摆运动的物理量

例1：如图2所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内做匀速圆周运动,则它们的( )。

A. 周期相同

B. 线速度的大小相等

C. 角速度的大小相等

D. 向心加速度的大小相等

图2

图3

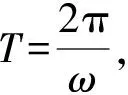
讨论：若不用ω2h=g结论解题,则先要对小球受力分析,如图3所示,小球受重力mg、绳子拉力FT,合力提供向心力，水平指向圆心。

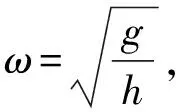
可见,用ω2h=g的结论可快速解答此类选择题。

2.2 确定两圆锥摆摆球的位置

例2：两根长度不同的细线下面分别悬挂两个小球,细线上端固定在同一点,若两个小球以相同的角速度,绕共同的竖直轴线在水平面内做匀速圆周运动,则两个摆球在运动过程中,相对位置关系图4中正确的是( )。

图4

解析：因两个小球以相同的角速度绕共同的竖直轴在水平面内做匀速圆周运动,根据圆锥摆的推论ω2h=g可得两球轨迹圆心到悬点的竖直高度h相等,两球应在同一水平面内运动,故B选项正确。

讨论：由于本题不涉及定量计算,因此本题直接用结论判断两球的相对位置简洁明了,体现出用该结论解题的优越性。

2.3 比较两圆锥摆与竖直方向的夹角

例3：如图5所示,“旋转秋千”中的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上,不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法中正确的是( )。

A.A的速度比B的大

B.A与B的向心加速度大小相等

C. 悬挂A、B的缆绳与竖直方向的夹角相等

D. 悬挂A的缆绳所受的拉力比悬挂B的小

图5

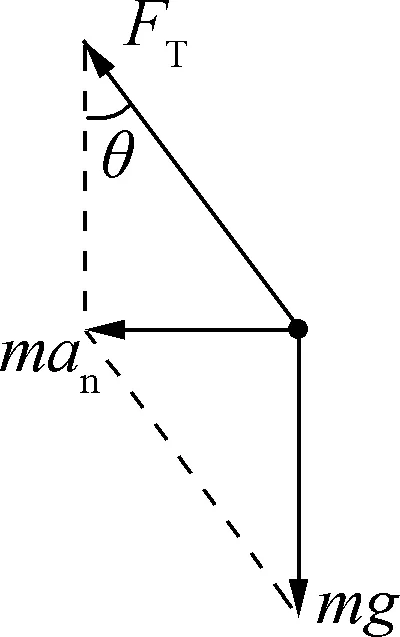
图6

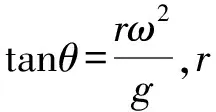
图7

图8

例4：游乐园里有一种叫“飞椅”的游乐项目,简化后的示意图如图8所示。已知飞椅用钢绳系着,钢绳上端的悬点固定在顶部水平转盘上的圆周上。转盘绕穿过其中心的竖直轴匀速转动。稳定后,每根钢绳(含飞椅及游客)与转轴在同一竖直平面内。图中P、Q两位游客悬于同一个圆周上,P所在钢绳的长度大于Q所在钢绳的长度,钢绳与竖直方向的夹角分别为θ1、θ2。不计钢绳的重力。下列判断正确的是( )。

A.P、Q两个飞椅的线速度大小相同

B. 无论两个游客的质量分别有多大,θ1一定大于θ2

C. 如果两个游客的质量相同,则有θ1等于θ2

D. 如果两个游客的质量相同,则Q的向心力一定小于P的向心力

讨论：推论ω2h=g适用于一切圆锥摆,此推论与圆锥摆的摆线长度、圆锥摆的摆球质量、悬线与竖直方向的夹角无关,解题时要明确h是圆锥摆的摆球运动轨迹圆心到转轴上悬线悬点(或悬线延长线与竖直轴交点)的高度。