低复杂度频域迭代均衡技术

王晓春，陈佳怡，董 超

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.陆军边海防学院，新疆 乌鲁木齐 830001；3.北京邮电大学，北京 100786)

0 引言

迭代均衡最早是受迭代信道译码思想产生的。随着Turbo码[1-2]的引入，信道译码器能够输出似然比软信息，该信道能够反映信道译码结果的可靠度。通过将信道译码软信息反馈到前端均衡器，均衡器的系数能够根据信道反馈的可靠性进行优化。根据信道译码的可靠性，在每次迭代处理过程中，前端均衡器的系数需要进行更新。随着迭代的进行，均衡器和译码器的性能最终收敛。该方法可以用于无线传输的多径信道中，该信道中存在的多径效应引入的符号间干扰，能够通过信道反馈辅助下的均衡加以消除[3-5]。在迭代均衡处理中，是以数据块为单位进行处理，每个数据块之前添加前缀，前缀的长度需要大于最大多径时延。通过引入前缀，使得每个数据块之间没有相互干扰，从而使得均衡处理能够在数据块之间独立进行。同时由于前缀的存在，使得信号均衡能够在频域进行，通过频域的等效处理，能够有效降低计算复杂度。

1 信号模型

本文的迭代均衡都是以数据块为处理单位进行，并需要用到频域计算，在均衡处理的过程中，需要用到快速傅里叶变换(FFT)。近年来，随着数字信号处理技术的发展和器件处理能力的提高，FFT往往能够通过数字处理芯片上的专用IP核实现。针对时域数据块，能够通过FFT变换，将其变换到频域，然后在频域进行相应的信号处理。根据前缀形式不同，数据块主要有循环前缀和导频前缀2种形式。

具有循环前缀的数据块结构如图1所示。

图1 具有循环前缀的数据块结构
Fig.1 The data block structure with cyclic prefix

如图1所示，在具有循环前缀的数据块中，数据长度等于N，该长度也是FFT的点数；数据块末尾L个数据符号，被复制到该数据块的起始位置，被称为循环前缀。循环前缀的长度L需要大于无线信道的最大多径时延。由于循环前缀的存在，对于一个数据块的数据来说，能够通过FFT，进行具有低复杂度特征的频域均衡。

具有导频前缀的数据块结构如图2所示。

图2 具有导频前缀的数据块结构
Fig.2 The data block structure with pilot prefix

从图2可以看出，每个数据块中数据的长度是M，导频长度为L，M+L之和N等于FFT的点数，导频的长度L需要大于无线信道的最大多径时延。对于相邻的数据块，采用的导频样式也是相同的。基于以上设置，对于总长为N的数据块来说，也能够通过FFT，进行低复杂度频域均衡。在实际的4G LTE和5G NR系统中，传输数据块采用的都是循环前缀的方式，因此以下的数学模型主要针对循环前缀的数据块展开。

假设FFT的点数为N，则针对循环前缀的数据块，其信号模型可以统一写为：

y=Hx+n，

(1)

式中，y∈N×1表示N维的接收信号；向量x∈N×1表示N维的发送信号向量；n∈N×1表示N维的噪声向量，其服从复高斯分布(0,n0IN)。由于循环前缀的存在，H∈N×N具有循环平移的形式，即H的每一行(列)都可以通过第一行(列)做循环平移获得，其具体表达式为：

(2)

式中，L表示时域上多径时延的长度。根据H的循环平移特性，其频域信道响应矩阵具有对角化特性

G=FHFH=diag{g0,g1,…,gN-1}。

(3)

对角线元素gk,0≤k≤N-1表示在第k个子载波上的信道响应，它的表达式为：

(4)

2 频域迭代均衡

迭代均衡算法可以在频域实现[6]。在迭代均衡当中，需要用到信道译码器反馈的外信息。根据前一节的定义，对于发送符号向量x中的第i个元素，表示为xi，0≤i≤N-1，还假设发送符号采用QPSK调制。因此，xi可以表示为：

(5)

式中，bi,1，bi,2分别表示xi在实部和虚部各自承载的比特。假设信道译码器反馈的外信息用似然比形式表示，则对应bi,1，bi,2的外信息似然比分别表示为lbi,1，lbi,2。在迭代均衡过程中，需要用到译码反馈以均衡和方差的形式进行表征。根据似然比，比特均衡和方差的计算公式为：

(6)

(7)

进一步，对应调制符号xi的均值和方差分别表示为：

(8)

vxi=0.5vbi,1+0.5vbi,2,0≤i≤N-1。

(9)

在后续的频域均衡中，需要用到式(8)和式(9)提供的均值和方差的信息。

(10)

(11)

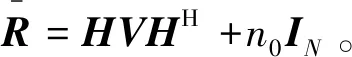
(12)

根据矩阵求逆公式，式(12)可以表示为：

(13)

通过收集所有的xi，均衡结果可以写成向量的形式：

(14)

式中，矩阵Λ是对角矩阵，其表达式为：

(15)

后续希望能够通过频域处理降低式(14)中均衡计算的复杂度。首先引入：

(16)

(17)

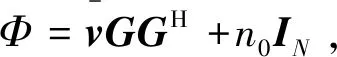
进一步，式(15)中包含的矩阵乘法也可以写成频域等价形式：

(18)

根据时—频域变换的形式，式(18)中计算得到的矩阵其对角线元素相同，因此式(15)可以进一步表示为：

(19)

因此，式(14)的均衡能够在频域实现，其频域处理的表达式为：

(20)

正是基于以上频域对角化特性，对于接收信号的均衡能够在频域实现，此时频域均衡的复杂度是O(NlogN)的，该复杂度同信道多径时延的长度无关。

3 仿真结果

Proakis C信道迭代均衡仿真结果如图3所示。

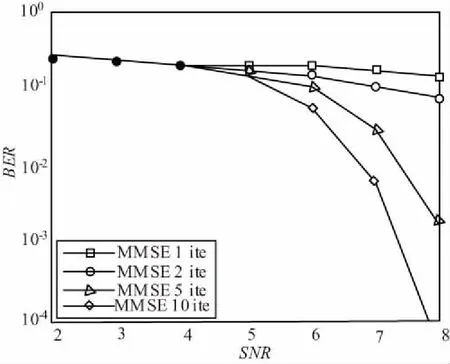
图3 Proakis C信道迭代均衡仿真结果Fig.3 The iterative equalization performance in proakis C channel

基于以上均衡算法进行了性能仿真。多径信道模型采用Proakis C信道，多项式为[13,15]8，码率为0.5，采用QPSK调制，数据块的长度N=1 024。

从图3的仿真结果可以看出，经过MMSE迭代均衡10次之后，接收端误比特率能够获得比较明显的性能增益。

4 最新进展

前述的MMSE均衡方法在多径衰落信道中具有较强的适用性，但是当信道多径干扰较为严重时，迭代收敛的速度较慢。为了能够有效加快收敛，文献[7]进一步引入了序列信息可靠度作为优化指标，通过Cholesky分解，实现信道译码软反馈下的序列符号检测。进一步，文献[8]通过引入双向判决反馈均衡，考虑判决反馈的可靠性，实现严重符号间干扰信道中的性能优化。

近年来，基于因子图的消息传递算法[9]被引入到符号间干扰信道的均衡中，尤其是Approximate Message Passing (AMP)算法[10]，Generalized Approximate Message Passing (GAMP)算法[11-12]，通过有效的数学近似，降低了复杂度，同时优化了检测性能。文献[13]表明，将GAMP算法用于循环前缀的数据块均衡，并与信道译码构成迭代接收机结构，其迭代收敛性和检测性能要优于文献[6]中的算法，并且该均衡算法能够在频域实现。

除此之外，基于期望传播(Expectation Propagation，EP)的检测算法，也能够被用于符号间干扰信道的均衡中。文献[14]将EP形式的均衡器加入到迭代接收机结构中，该均衡器是在时域实现的；文献[15]采用了EP形式的判决反馈均衡器；文献[16]中的EP均衡器具有时域抽头延时线的结构；文献[17]提出的EP均衡器能够在频域实现，降低了均衡复杂度。

5 结束语

迭代均衡是随着Turbo码的出现而产生的，其主要设计思想是将信道译码软信息输出，反馈到前端的均衡器，用于重构干扰分量，从而消除多径、多天线、多用户传输带来的干扰，提高接收机的可靠性。随着Turbo码、LDPC码技术的不断发展，信道译码能够提供的软反馈信息的可靠性不断得到改善，同时前端的均衡器结合频域均衡、判决反馈均衡等技术也在不断向前发展。随着基础信号处理器件和芯片计算能力的不断提高，迭代均衡已经成为提升接收机性能的一条重要技术途径，并在实用化系统中得到了广泛应用。