红边位置改进算法的冬小麦叶绿素含量反演

钱彬祥，黄文江，叶回春，孔维平，任　淯，邢乃琛，焦全军

·农业信息与电气技术·

红边位置改进算法的冬小麦叶绿素含量反演

钱彬祥1,2,3，黄文江2,3※，叶回春2,3，孔维平4，任淯1,3，邢乃琛1,3，焦全军2,3

（1. 中国科学院大学，北京 100049；2. 海南省地球观测重点实验室，三亚 572029；3. 中国科学院空天信息创新研究院，数字地球重点实验室，北京 100094； 4. 中国科学院空天信息创新研究院，定量遥感信息技术重点实验室，北京 100094）

植被反射光谱的红边位置对叶绿素含量高度敏感，利用遥感数据建立基于红边位置的作物叶绿素含量反演模型，可实现大范围作物及时的长势监测。该研究以冬小麦为研究对象，在学习6种经典红边位置求解算法的基础上，提出牛顿-切比雪夫插值法和牛顿八点插值法2种改进红边位置求解算法。根据不同算法的红边位置分布特征综合分析了改进算法的优缺点，并在此基础上建立基于红边位置的冬小麦叶绿素含量反演模型。结果表明，与传统算法相比，2种改进算法均显著改善了双峰现象和红边位移，且基于改进算法的模型预测值与叶绿素含量实测值的决定系数>0.619，较最大一阶导数法，牛顿八点插值法提高了6.321%～9.947%，牛顿-切比雪夫插值法提高了5.024%～10.480%，具有更高的精度。同时，在2种改进算法中，牛顿八点插值法具有更高的稳定性与实用性。研究结果为植被理化参数反演与农业生产应用提供理论与技术支撑。

算法；遥感；模型；冬小麦；叶绿素反演；牛顿-切比雪夫插值法；牛顿八点插值法；红边位置

0 引 言

叶绿素含量是一种综合反映作物受外界环境胁迫情况、光合作用能力强弱和新陈代谢旺盛程度的非常敏感的指示剂[1-2]。研究表明，作物反射光谱的红边位置（Red Edge Position，REP）与叶绿素含量具有相当高的相关关系，是作物生理生化参数遥感反演的一个重要指标[3-5]。建立基于红边位置的作物叶绿素含量反演模型，为实现大面积作物及时的长势监测提供了一种快速而实用的方法[6]。红边波段一般认为在可见光波段的660～770 nm范围内，由于带宽较宽，不利于其与作物理化参数相关模型的建立，所以通常用位于红光-近红外波段作物反射光谱的突变点来精确定位红边位置[7-8]。

目前，红边位置求解算法可分为基于微分插值和基于曲线拟合两大类。基于曲线拟合思想的算法提出的更早，Miller等[3]提出倒高斯模型法（Red Edge Position calculated by Inverted Gaussian，REP_IG），即用一条倾斜的倒高斯曲线近似红边波段范围内的作物反射光谱，该模型较为复杂，需先经等价变换才能进行下一步解算。为了简化计算，Demetriades-Shah等[9]用红边波段范围内作物反射光谱的一阶导数最大值对应的波段位置确定红边位置。Dawson等[10]研究表明最大一阶导数法（Red Edge Position calculated by Maximum First Derivative，REP_MFD）提取红边位置的精度取决于传感器平台的波段范围和光谱分辨率，为减少红边位置求解精度对光谱分辨率的过度依赖，提出了拉格朗日三点内插法（Red Edge Position calculated by Lagrange，REP_LAGR）。Clevers等[11]认为拉格朗日三点内插法只适用于粗分辨率光谱，且不能解决红边位置求解过程中存在双峰现象（bimodal phenomenon，BP）的问题，为此提出了线性四点内插法（Red Edge Position calculated by Linear Four-Point Insert，REP_LFPI），该方法是最简单、易行的红边位置求解算法，只需要4个波段和简单的线性插值运算。此外，Pu等[12]采用5次多项式拟合作物反射光谱，多项式一阶差分最大值对应的波段位置即为红边位置，并利用实测光谱数据验证了该方法的合理性。Lin等[13]开展了拉格朗日三点内插法和多项式拟合法（Red Edge Position calculated by Polynomial fitting，REP_POLY）的精度对比研究，发现拉格朗日三点内插法的精度取决于波段组合，且对噪音尤为敏感，而多项式拟合法的适用性更高、稳定性更强。Cho等[14]为减少双峰现象带来的不稳定性的影响，提出了线性外推法（Red Edge Position calculated by Line Extrapolate，REP_LE）。陈西亮等[4]将牛顿插值法（Red Edge Position calculated by Newton Interpolation，REP_NI）应用于红边位置求解过程，利用6个等距的红边波段反射光谱数据内插出红边位置，求解精度位于倒高斯模型法和线性四点内插法之间。陈西亮等[4]的研究中存在以下不足：1）选取ENVI自带的USGS植被波谱库中的矮松树、山杨树、草坪和蓝云杉4种植被的4条反射光谱做分析，数据量过少，分析结果受偶然误差和样本选取的影响较大，且与实际生产相脱离，研究缺乏普适性；2）由于缺乏试验数据，无法分析不同算法求解出的红边位置的分布特征（如双峰现象、红边位移），仅利用红边位置的相对误差来衡量算法的优劣缺乏科学性；3）没有将新算法与作物生理生化参数遥感反演相结合，无法检验新算法的实用性。

与传统算法相比，牛顿插值法具有明显优势。传统算法普遍对传感器提出光谱分辨率高、采样均匀的要求，且求解的红边位置存在双峰现象、红边位移（Displacement of Red Edge Position，REPD）和精度不足等缺点。牛顿插值法属于微分插值方法，相较于曲线拟合方法需要的数据量更少，并且能够完全保留原始数据，以及引入差分（Difference，DF）和差商（Difference Quotient，DFQ）的概念，可以计算非等距节点的光谱反射率。同时，与拉格朗日插值法相比较，牛顿插值法不仅克服了每增加一个节点整个计算必须重新开始的缺点，而且可以节省乘、除法运算的次数，提高了计算速度[15]。

鉴于牛顿插值法的优越性以及前人研究工作还有待进一步完善，本研究以冬小麦为试验对象，采用数值分析技术，在学习经典算法的基础上提出2种改进的红边位置求解算法：牛顿八点插值法（Red Edge Position calculated by Newton Eight-Point Interpolation，REP_NEPI）和牛顿-切比雪夫插值法（Red Edge Position calculated by Newton-Chebyshev-Node Interpolation，REP_NCNI），并进行两者的综合比较，拟建立更高精度的基于红边位置的冬小麦叶绿素含量反演模型。研究结果可以为植被理化参数遥感反演增添新的理论依据，为农业工程领域的冬小麦叶绿素含量监测、长势评估等实际生产应用提供新的技术支撑。

1 材料与方法

1.1 研究区概况及试验设计

研究区位于北京市昌平区小汤山国家精准农业示基地（40°11′N，116°26′E），气候类型为暖温带半湿润大陆季风气候。本研究选取2002—2003年和2018—2019年小麦生长季内不同品种、不同肥水处理下的冬小麦连续开展了野外测量试验，在其关键生育期采集常规农学数据与近地高光谱数据。具体处理方式如下：

1）小麦品种：2002—2003年选用3种不同株型、籽粒品质的冬小麦，包括株型紧凑、籽粒品质弱筋型的“京411”，株型松散、籽粒面筋质量好的“中优9507”和株型与籽粒品质中间型的“京冬8”[7-8]。2018—2019年选用株型半紧凑、籽粒面筋质量好的“轮选167”和株型紧凑、籽粒品质中间型的“京冬18”。

2）肥水处理：2002—2003年的研究区共有48个肥水处理小区，各小区面积为32.4 m×30 m，在试验区内对不同品种的冬小麦分别进行肥水胁迫处理。4个梯度施肥处理：0N处理，返青期至成熟期不施肥；②1N处理，返青期和拔节期各追施尿素50 kg/hm2；8N处理，返青期和拔节期各追施尿素200 kg/hm2；④14N处理，返青期和拔节期各追施尿素350 kg/hm2[7-8]。4个梯度供水处理：0水处理，全生育期不灌溉；②1水处理，全生育期灌水225 m3/hm2；2水处理，全生育期灌水450 m3/hm2；3水处理，全生育期灌水675 m3/hm2[7-8]。2018—2019年的研究区共有32个肥水处理小区，各小区面积为10 m×15 m，在试验区内正常供水，对不同品种的冬小麦进行肥胁迫处理：N0处理，返青期至成熟期不施肥；N1处理，基肥（2018年9月）97.5 kg/hm2和拔节期（2019年4月）追肥97.5 kg/hm2；N2处理，基肥（2018年9月）195 kg/hm2和拔节期（2019年4月）追肥195 kg/hm2；N3处理，基肥（2018年9月）292.5 kg/hm2和拔节期（2019年4月）追肥292.5 kg/hm2。

3）测定项目：不同生育时期的冠层光谱反射率、配套的数码照片和包括叶绿素含量（mg/g）、叶面积指数在内的常规田间调查农学参数。

4）测定时期：包括返青期（3月25日前后）、拔节期（4月15日前后）、挑旗期（4月25日前后）、开花期（5月10日前后）、灌浆中期（5月20日前后）、灌浆后期（5月30日前后）在内的冬小麦6个关键生育期。通过询问试验区内经验丰富的技术人员，获取试验区内该年度冬小麦的长势情况、降水量和气温变化等信息，并就此制定具体的测量时间与试验方案。

1.2 光谱和农学参数测定

小麦冠层光谱采用美国ASD公司生产的FieldSpec FR光谱辐射仪测定[16]，选取晴朗无云、风力较小的10:30－14:00（北京时间）进行，采样范围为350～2 500 nm，采样间隔为1 nm。测定时，探头在距离冠层约1 m处垂直向下观测，测定前后用标准参考板校正，每个点重复测定20次，取全部测数的均值作为该点的冠层光谱反射率。同时，在目标区域附近利用打孔器获取测试样品，称量后在黑暗环境下浸泡于95%乙醇溶液中24～48 h，使用UV765PC型分光光度计测定溶液在可见光440、649和665 nm处的吸光度值，并由此计算叶绿素含量（mg/g）。

1.3 红边位置求解算法

1.3.1 传统的红边位置求解算法

传统的红边位置求解算法主要有以下6种：

1）最大一阶导数法

在红边波段范围内，植被光谱曲线反射率的一阶差分最大值对应的波长位置即为红边位置[17]，其计算如式（1）和式（2）所示：

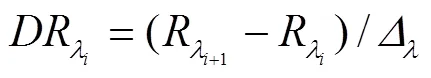
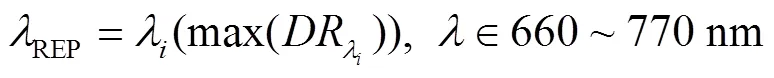
2）倒高斯模型法

采用一条倾斜的倒高斯曲线近似红边范围内的植被反射光谱，倒高斯曲线函数表达式[18]如式（3）和式（4）所示：

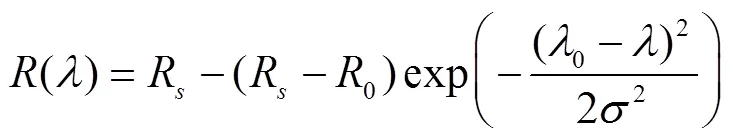
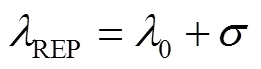
式中()为倒高斯函数；R为植被光谱反射率在红边波段范围内的最大值；0、0分别为红边位置范围内植被光谱反射率最小值及其所对应的波长位置；为高斯模型标准差系数，nm。

3）拉格朗日三点内插法

拉格朗日三点内插法是一种适用于粗采样光谱的三点插值算法，具体原理是利用二次多项式拟合植被反射率光谱一阶导数[16]，如式（5）和式（6）所示：

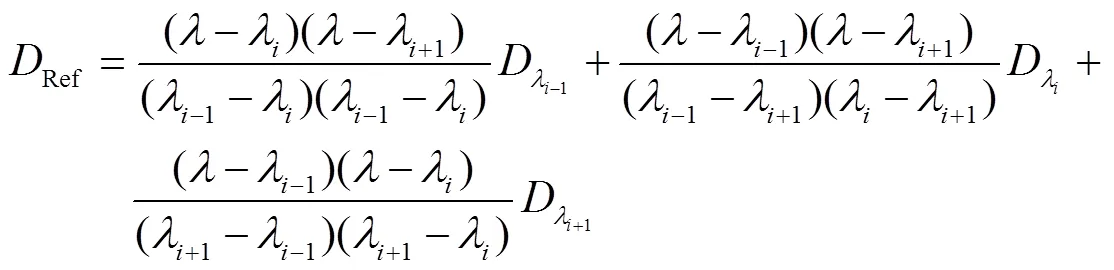
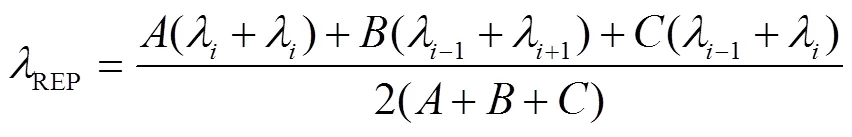
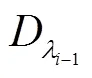
4）线性四点内插法

其假设红边波段范围内的植被反射率光谱近似为一条直线，红边位置由4个特征点的反射率值（670、700、740和780）内插得到[19]，如式（7）和式（8）所示：

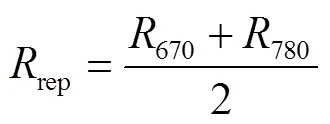
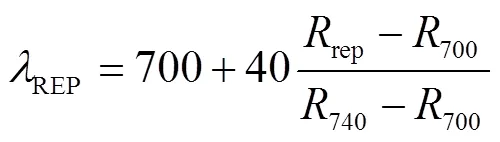
式中rep为拐点反射率。

5）多项式拟合法

多项式拟合法是利用高次多项式高精度逼近红边波段的植被光谱曲线，经多次试验表明9阶多项式的拟合效果最好，均方根误差<0.15和决定系数>0.999 93，其计算如式（9）和式（10）所示：

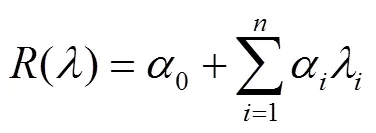
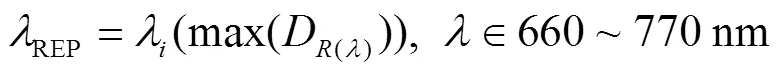
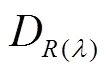
6）线性外推法

基于一阶导数光谱在远红色（680～700 nm）和近红外（725～760 nm）区域的2条直线线性外推红边位置[20]，如式（11）所示：

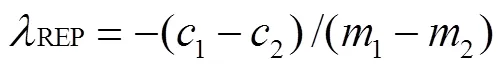
式中1、1分别为远红色波段直线的截距与斜率；2、2分别为近红外波段直线的截距与斜率。

1.3.2 本研究改进的红边位置求解算法

在学习传统方法的基础上，本研究运用数值分析技术将牛顿插值法应用到红边位置的求解过程中。在利用插值多项式进行近似逼近时，通常认为构建多项式的原始插值节点越多、多项式阶数越高，多项式逼近原始数据的效果就越好，可事实并非如此。龙格在20世纪初就证明了高次插值多项式具有病态性：基于等距节点的高阶插值多项式插值点数量越多，多项式在逼近区间两端产生的振荡现象就会越明显，即插值结果越偏离原函数[4]，这种病态性现象被称为龙格现象[21]。龙格现象在牛顿插值法中尤为明显，为了有效减少龙格现象的影响，本研究提出了以下2种解决方法：一是选择适当的插值次数；二是借助切比雪夫零点替换等距节点。

1）牛顿八点插值法

为确定适当的插值次数，本研究进行多次试验得出：在红边位置范围内采集跨度为20 nm左右的8个插值点的插值效果最好，8个插值点分别位于651、671、691、711、731、751、771和790 nm处。利用差商原理将8个插值点代入牛顿插值多项式求取各阶系数[4]如式（12）所示：

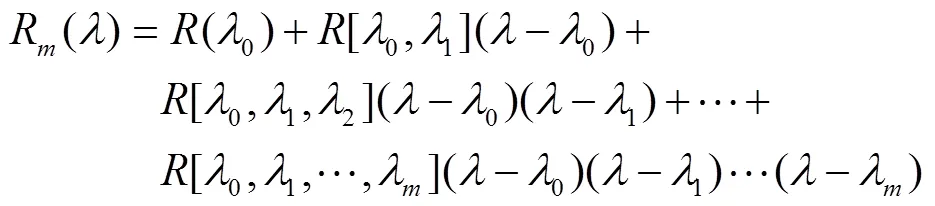
2）牛顿-切比雪夫插值法

牛顿八点插值法中的节点选取比较固定，会降低算法的实用性，将切比雪夫零点应用到插值节点选取中，用零点替换等距节点，可以使得插值点的选取更具有科学性和普适性[22]，其计算如式（13）和式（14）所示：

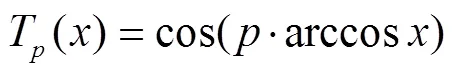
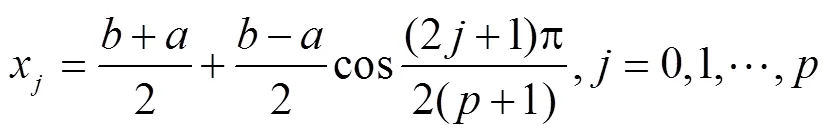
式中T()为切比雪夫多项式；、分别为零点区间的上下限；x为零点解。

进行上述9种算法核心思想的对比，如表1所示。

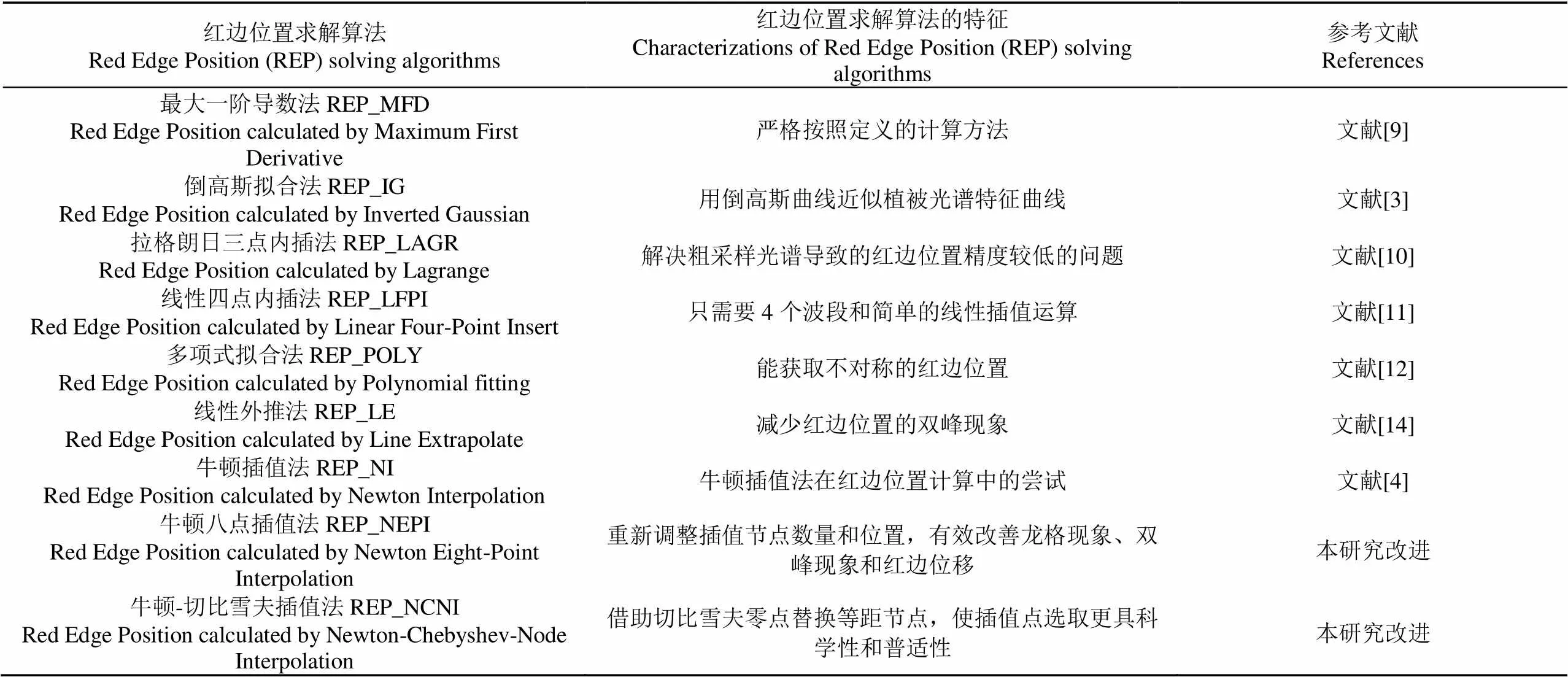
表1 8种红边位置求解算法的特征描述

1.4 叶绿素含量反演方法与精度评价指标

研究采用红边位置分布特征的描述统计量对不同算法进行特性分析，这些统计量包括最值、平均值、相对误差（Relative Error，RE）等。并运用最小二乘回归原理（Least Square Regression，LSR）建立基于不同算法红边位置的冬小麦叶绿素含量反演模型，对反演模型的预测值与叶绿素含量实测值进行线性拟合，评定各个模型的精度，精度评价指标包括拟合方程的斜率、截距、决定系数（coefficient of determination，2）、均方根误差（Root Mean Squared Error，RMSE）和标准均方根误差（Normalized Root Mean Squared Error，NRMSE）。各指标计算如式（15）～式（18）所示：

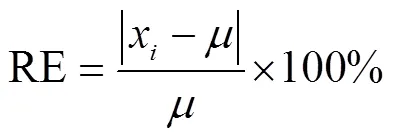
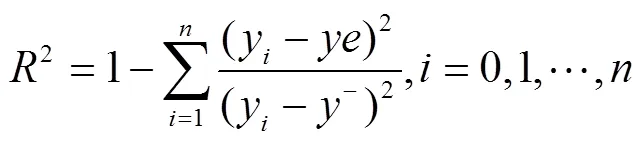
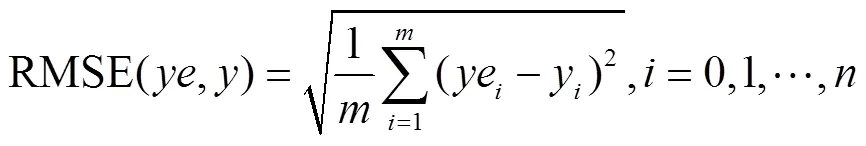
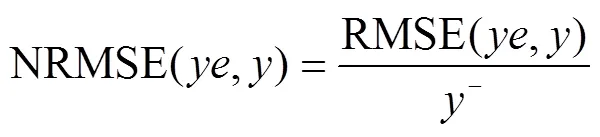
式中x为红边位置的相对误差；为各类算法所求的红边位置，nm；此处，、y分别为植被光谱反射率实测值的数组和元素；、ye分别为植被光谱反射率拟合值的数组和元素；−为植被光谱反射率实测值的平均值；和分别表示实测数据的编号和总数。一般认为，当NRMSE≤0.1时，认为模型的拟合优度很好；当0.10.3时，认为模型的拟合优度较差[23-25]。

挑旗期、开花期、灌浆中期是冬小麦生长周期中新陈代谢最为旺盛的3个时期，本研究选取以上3个生育期的原始试验数据进行研究，其中，2002－2003年的样本数据（样本数为136）用于不同算法的特性分析与冬小麦叶绿素含量反演模型的建立，2018－2019年的样本数据（样本数为64）进行模型的检验。

2 结果与分析

2.1 不同算法的特性分析

实现8种红边位置求解算法，并对建模集数据进行处理，得到不同算法红边位置的分布特征和算法特性（表2）。同时，为了直观地观察不同算法的红边位移与双峰现象，绘制出的红边位置与叶绿素含量的散点图（图1）。各种算法红边位置的最小值在694～717 nm，主要集中在694～706 nm，线性四点内插法的最小值显著偏大（717 nm）；红边位置的最大值在729～736 nm，主要集中在735～736 nm，倒高斯模型法的最大值相对偏小（729 nm）；红边位置的平均值在719.5～727.2 nm，主要集中在725.4～727.2 nm，倒高斯模型法和线性外推法的最大值明显偏小，分别为715.9和721.9 nm。红边位置的变幅是评价红边算法对植被反射光谱敏感程度的重要指标之一，在一定程度上，红边位置的变幅越大，说明该算法对植被光谱曲线越敏感；变幅较小会存在红边位置的饱和现象。以上算法红边位置的变幅在14～41 nm，主要集中在30～41 nm，线性四点内插法的变幅明显偏小（14 nm）。考虑到最大一阶导数法是严格遵守红边位置定义的算法，所以将其计算结果作为参考标准计算得到其他算法的RE在0～0.882%，主要集中在0～0.179%。其中，拉格朗日三点内插法的RE最小，可忽略不计，倒高斯模型法和线性外推法的RE较大，分别为0.882%和0.551%。

双峰现象和红边位移对叶绿素含量反演模型的建立是非常不利的。根据散点图中红边位置与叶绿素含量的分布特征可知，最大一阶导数法、拉格朗日三点内插法、倒高斯模型法和九阶多项式拟合法在进行红边位置求解时均出现明显的双峰现象，即红边位置出现在中心波长分别为698和730 nm的集中区。与之相比，其他4种方法在不同程度上削减了双峰现象的不利影响，且牛顿插值法的效果最佳。同时，线性四点内插法的红边位置向长波方向收拢（不是红移，是收拢，整体集中在720～730 nm）；倒高斯模型法、线性外推法存在红边位置向短波方向位移（蓝移）。

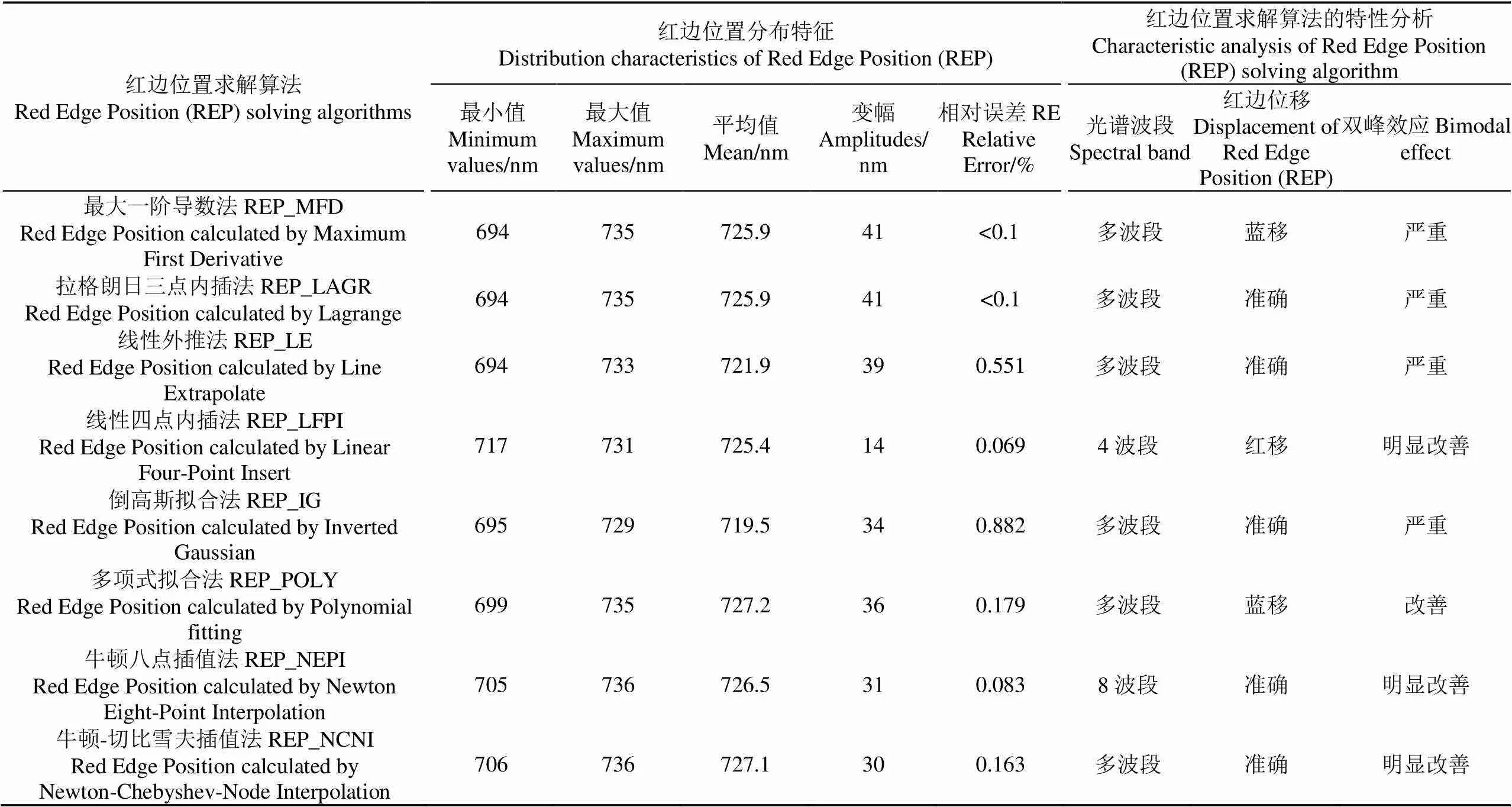
表2 不同红边位置求解算法的特性分析

注：进行不同红边位置求解算法的特性分析所用的数据来源于2002－2003年的试验数据（样本数为136）。

Note: Data used to analyze the characteristics of different Red Edge Positions (REP) solving algorithms come from the experimental data from 2002 to 2003 (The number of samples are 136).

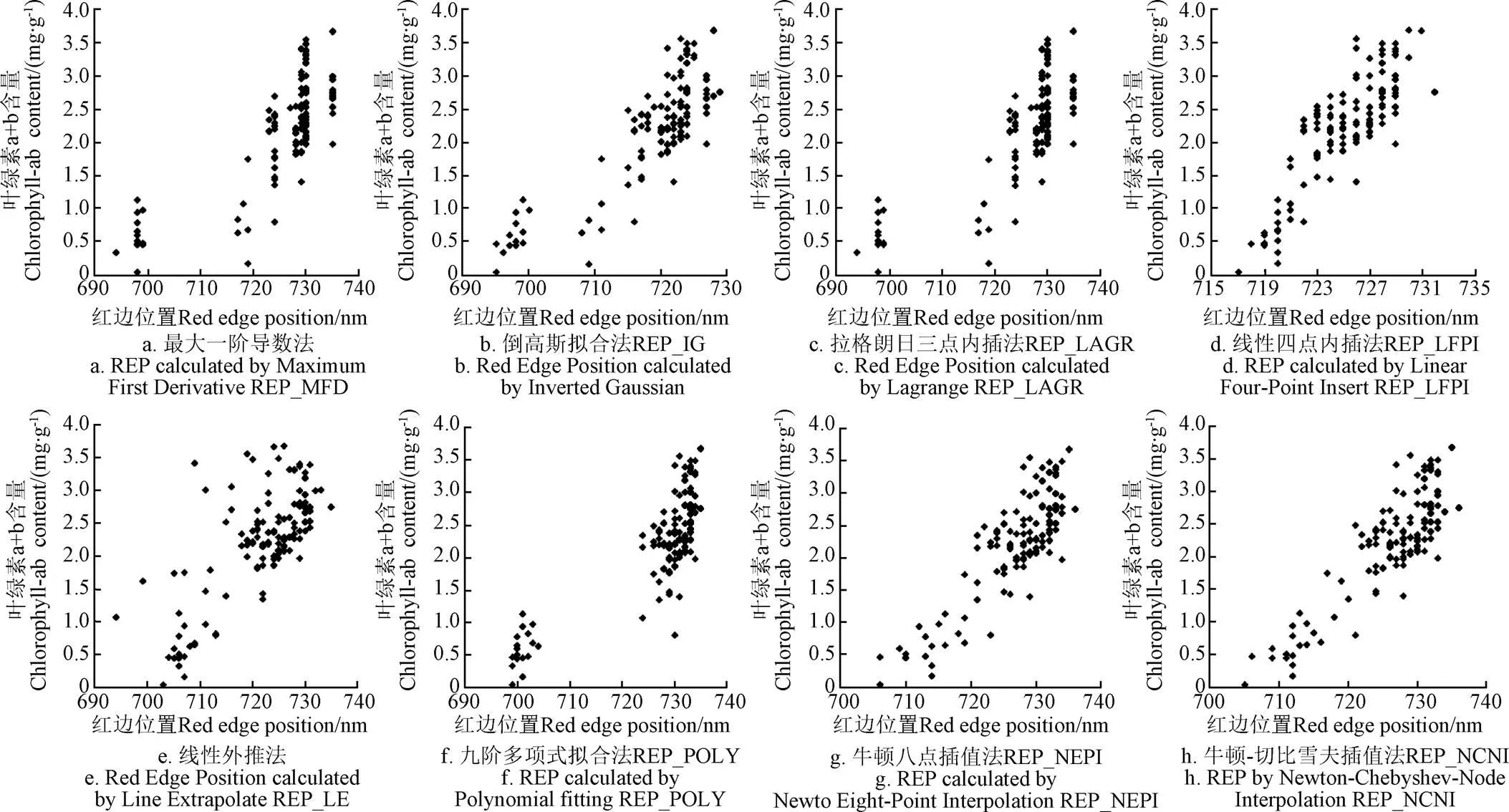
注：用于制作散点图的数据来源于2002－2003年的试验数据（样本数为136）。

经以上分析，可以得到以下结论：1）最大一阶导数法、拉格朗日三点内插法的红边位置变幅最大（41 nm），对叶绿素含量十分敏感，然而存在明显的双峰现象；2）倒高斯模型法的结果介于695～729 nm之间，平均值最小（719.5 nm），整体向短波方向移动（蓝移），且RE最大（0.882%）；3）线性四点内插法的结果介于717～731 nm之间，整体向长波方向收拢，平均值为725.4 nm，红边位置变幅最小（14 nm），对叶绿素含量变化不敏感；4）线性外推法的结果变幅较好（37.1 nm），但平均值偏低（721.9 nm），整体向短波方向移动（蓝移），且RE较大（0.551%）；5）九阶多项式拟合法的结果整体较好，不过双峰现象最为显著；6）牛顿八点插值法和牛顿-切比雪夫插值法的结果最小值偏大（705和706 nm），平均值、变幅和RE较为理想，并有效克服了双峰现象和红边位移。

2.2 基于红边位置的冬小麦叶绿素含量反演

2.2.1 基于红边位置的冬小麦叶绿素含量反演模型的建立

利用2002－2003年冬小麦的叶绿素a（Chlorophyll-a，Chla）、叶绿素b（Chlorophyll-b，Chlb）和叶绿素a+b（Chlorophyll-ab，Chlab）含量实测数据与红边位置计算结果进行相关性分析，得到基于不同算法的冬小麦叶绿素含量反演模型（表3），研究表明8种方法计算出的红边位置和叶绿素含量均有很好的相关性。

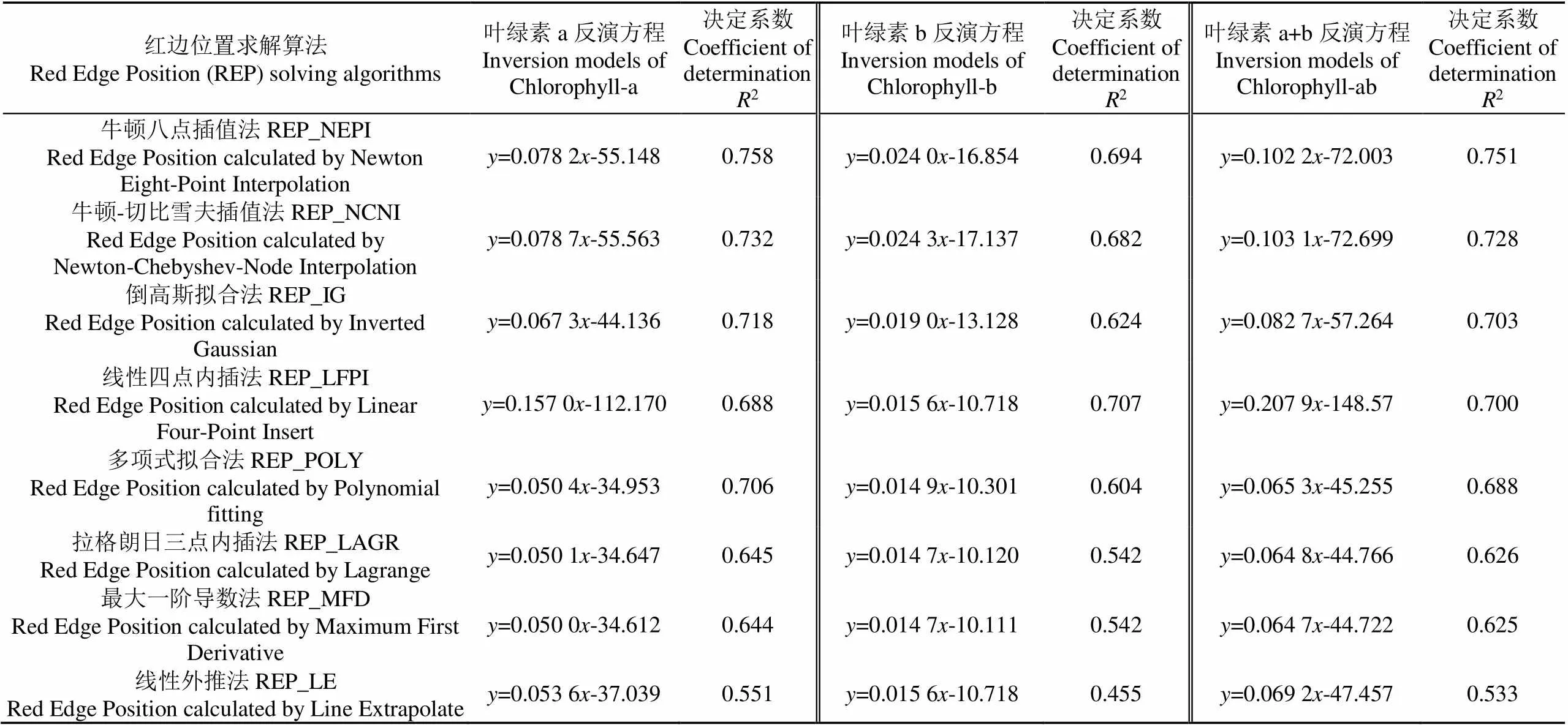
表3 基于不同红边位置求解算法的冬小麦叶绿素含量反演模型

注：建立不同红边位置求解算法的冬小麦叶绿素反演模型的数据来源于2002—2003年的试验数据（样本数为136）。

Note: Data used to build the inversion models of winter wheat chlorophyll content based on different Red Edge Position (REP) solving algorithms are the experimental data from 2002 to 2003 (The number of samples are 136).

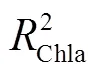
2.2.2 基于红边位置的冬小麦叶绿素含量反演模型的精度评定

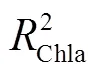
同时，基于几种算法建立的Chlab预测值与测量值的拟合方程式的斜率在0.406～1.191，截距在−1.524～3.118。其中，线性四点内插法和牛顿八点插值法的斜率分别为1.052和0.839，接近于1，截距分别为−0.101和0.378，接近于0，说明基于以上2种方法建立的反演模型的预测值能够高精度接近叶绿素含量实测值。相比之下，牛顿-切比雪夫插值法存在系统误差，其斜率在0.498～0.628之间，与理论值不相符。

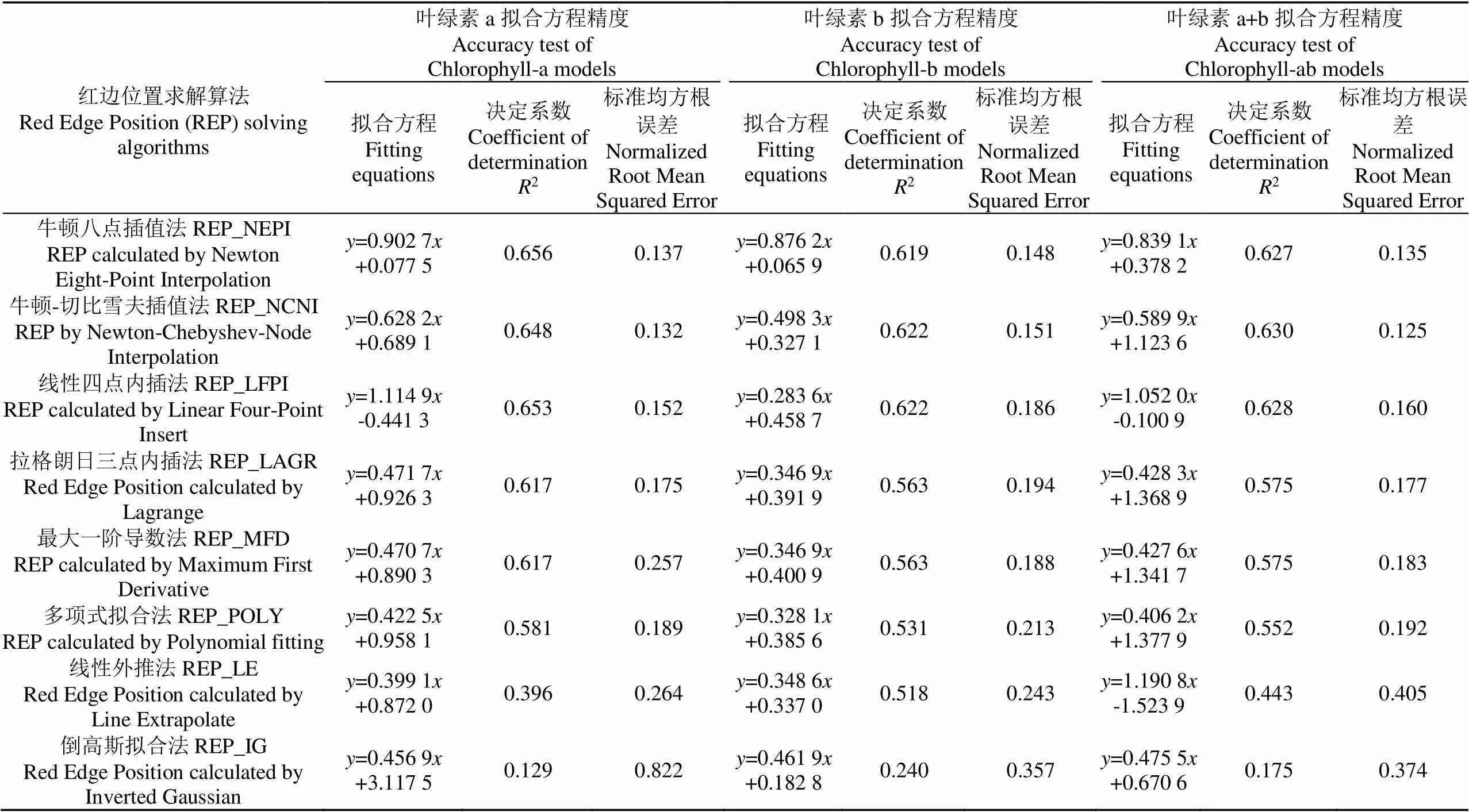
表4 基于不同红边位置求解算法的冬小麦叶绿素含量反演模型的精度检验

注：反演模型的精度检验数据来源于2018－2019年的试验数据（样本数为64）。

Note: The accuracy test data of the inversion model comes from the test data from 2018 to 2019 (The number of samples are 64).

3 讨 论

3.1 改进算法的性能评述

不难发现，与传统方法相比，改进方法在改善双峰现象和红边位移方面具有显著优势。线性四点内插法在改善双峰现象上的效果同样明显，但其红边位置变幅在8种算法中最小（14 nm），对叶绿素含量变化不敏感，而且存在红边位置整体向长波收拢，这对叶绿素反演模型的建立是不利的。考虑到拟合方程的斜率与截距，牛顿-切比雪夫插值法便暴露出其缺点，这可能与切比雪夫零点的选取区间过大导致其出现系统误差有关，下一步可以缩小零点区间，验证切比雪夫零点替换等距节点的科学性。同时，牛顿-切比雪夫插值法对光谱分辨率有较高的要求，很大程度上限制了其应用范围，而牛顿八点插值法不仅继承了牛顿插值法的优越性，而且融合了线性四点内插法对插值点需求少的特性，具有更高的精度、稳定性和实用性。综合考虑算法特性和各项精度指标，研究认为牛顿八点插值法优于传统算法和牛顿-切比雪夫插值法。

3.2 基于红边参数的冬小麦叶绿素含量反演模型的评价

8种算法拟合方程的2（0.396～0.656）普遍低于反演方程的2（0.455～0.758）的现象，是由于2002－2003和2018－2019年试验区内的冬小麦品种、长势与生境状况不完全相同，对模型的适用性产生了一定的影响。下一步可以在同一实验条件下，设置建模组与验证组，以期提高模型的精度。

4 结 论

本研究以冬小麦为研究对象，采用最小二乘回归分析方法，在实现6种经典红边位置求解算法的基础上，将牛顿插值法应用于红边位置求解，提出牛顿八点插值法和牛顿-切比雪夫插值法；并根据不同算法的红边位置分布特征综合分析了新旧算法的优缺点，对比了不同算法的综合属性信息；此外，建立了基于红边参数的冬小麦叶绿素含量反演模型，进行了叶绿素含量反演模型的预测值与实测值的线性拟合分析。通过以上研究得出，1）本研究提出的牛顿八点插值法和牛顿-切比雪夫插值法不仅有效地改善了红边位置求解时的双峰现象和红边位移，具有更高的精度与稳定性，而且使用牛顿插值法建立的叶绿素含量反演模型的决定系数（coefficient of determination，2）较其他方法高，牛顿八点插值法和牛顿-切比雪夫插值法的2分别为0.728和0.751；2）基于改进算法反演模型的预测值与叶绿素含量实测值的拟合方程2较其他方法高，均>0.619；标准均方根误差（Normalized Root Mean Squared Error，NRMSE）较其他方法小，均<0.151，即模型优度较好；3）同时，研究表明牛顿八点插值法比牛顿-切比雪夫插值法具有更高的精度、稳定性和实用性；4）关于牛顿-切比雪夫插值法中零点区间的选取和利用切比雪夫零点替换等距节点的科学性还有待进一步研究。

根据本研究对不同红边算法的红边位置分布特征分析、算法的综合属性信息对比以及基于红边参数的冬小麦叶绿素含量反演模型的精度评定，可以认为将牛顿插值法应用到冬小麦的红边位置计算和叶绿素含量反演的效果优于传统方法。此外，考虑到牛顿八点插值法计算红边位置只需要8个特定的光谱波段，为制作简易的作物叶绿素含量测定传感器提供了理论基础。

[1]Velichkova K, Krezhova D. Extraction of the red edge position from hyperspectral reflectance data for plant stress monitoring [C]//10th Jubilee International Conference of the Balkan Physical Union, 2019.

[2]Ptushenko V, Ptushenko O, Tikhonov A. Chlorophyll fluorescence induction, chlorophyll content, and chromaticity characteristics of leaves as indicators of photosynthetic apparatus senescence in arboreous plants[J]. Biochemistry, 2014, 79(3): 260-272.

[3]Miller J R, Hare E W, WU J. Quantitative characterization of the vegetation red edge reflectance 1. An inverted-Gaussian reflectance model[J]. International Journal of Remote Sensing, 1990, 11(10): 1755-1773.

[4]陈西亮，张佳华. 牛顿插值法在植被红边拟合中的应用[J]. 湖北农业科学，2016，55(7)：1828-1831.

Chen Xiliang, Zhang Jiahua. Application of Newton interpolation method in red edge fitting of vegetation[J]. Hubei Agricultural Science, 2016, 55(7): 1828-1831. (in Chinese with English abstract).

[5]黄林生，江静，黄文江，等. Sentinel-2影像和BP神经网络结合的小麦条锈病监测方法[J]. 农业工程学报，2019，35(17)：178-185.

Huang Linsheng, Jiang Jing, Huang Wenjiang, et al. Sentinel-2 imaging and BP neural network monitoring method for wheat stripe rust[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(17): 178-185. (in Chinese with English abstract).

[6]Sun Yuanheng, Qin Qiming, Ren Huazhong, et al. Red-edge band vegetation indices for leaf area index estimation from Sentinel-2/MSI imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(2): 826-840.

[7]Curran P J, Dungan J L, Macler B A, et al. The effect of a red leaf pigment on the relationship between red edge and chlorophyll concentration[J]. Remote Sensing of Environment, 1991, 35(1): 69-76.

[8]黄文江，王纪华，刘良云，等. 冬小麦红边参数变化规律及其营养诊断[J]. 遥感技术与应用，2003(4)：206-211.

Huang Wenjiang, Wang Jihua, Liu Liangyun, et al. Variation of red border parameters in winter wheat and its nutritional diagnosis[J]. Remote sensing technology and Applications, 2003(4): 206-211. (in Chinese with English abstract).

[9]Demetriades-Shah T H, Steven M D, Clark J A. High resolution derivative spectra in remote sensing[J]. Remote Sensing of Environment, 1991, 33(1): 55-64.

[10]Dawson T P, Curran P J. Technical note A new technique for interpolating the reflectance red edge position[J]. International Journal of Remote Sensing, 1998, 19(11): 2133-2139.

[11]Clevers J G P W, De Jong S M, Epema G F, et al. The use of the MERIS standard band setting for deriving the red edge index[J]. International Journal of Remote Sensing, 2002, 23(16): 3169-3184.

[12]Pu R, Peng G, Biging G S, et al. Extraction of red edge optical parameters from Hyperion data for estimation of forest leaf area index[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(4):916-921.

[13]Lin L, Ustin S L, Lay M. Application of AVIRIS data in detection of oil-induced vegetation stress and cover change at Jornada, New Mexico[J]. Remote Sensing of Environment, 2005, 94(1): 1-16.

[14]Cho M A, Skidmore A K. A new technique for extracting the red edge position from hyperspectral data: The linear extrapolation method[J]. Remote Sensing of Environment, 2006, 101(2): 181-193.

[15]何天荣. 牛顿插值法计算函数值的优缺点分析[J]. 考试与评价，2016(6)：70.

He Tianrong. Analysis of advantages and disadvantages of Newton interpolation method for calculating function values[J]. Examination and Evaluation, 2016(6): 70. (in Chinese with English abstract)

[16]曹中盛，李艳大，叶春，等. 基于高光谱的双季稻分蘖数监测模型[J]. 农业工程学报，2020，36(4)：185-192.

Cao Zhongsheng, Li Yanda, Ye Chun, et al. Monitoring model of tiller number of double cropping rice based on hyperspectrum[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(4): 185-192. (in Chinese with English abstract).

[17]Ghule A, Deshmukh R R, Gaikwad C. MFDS-m red edge position detection algorithm for discrimination between healthy and unhealthy vegetable plants[J]. Recent Trends in Image Processing and Pattern Recognition, 2019, 7(1): 372-379.

[18]高兴，李斐，杨海波，等. 基于红边位置的马铃薯植株氮浓度估测方法研究[J]. 植物营养与肥料学报，2019，25(2)：134-148.

Gao Xing, Li Fei, Yang Haibo, et al. Study on nitrogen concentration estimation method of potato plants based on red edge location[J]. Journal of Plant Nutrition and Fertilizer, 2019, 25(2): 134-148. (in Chinese with English abstract).

[19]丁永军，张晶晶，李修华，等. 基于光谱红边位置提取算法的番茄叶片叶绿素含量估测[J]. 农业机械学报，2016，47(3)：292-297.

Ding Yongjun, Zhang Jingjing, Li Xiuhua, et al. Estimation of chlorophyll content in tomato leaves based on spectral red edge location extraction algorithm[J]. Journal of Agricultural Machinery, 2016, 47(3): 292-297. (in Chinese with English abstract)

[20]郝瑞娟，王周锋，王文科，等. CO2胁迫下大豆叶片红边位置最优算法的研究[J]. 大气与环境光学学报，2016，11(1)：51-59.

Hao Ruijuan, Wang Zhoufeng, Wang Wenke, et al. Study on the optimal algorithm of red edge position for soybean leaves under CO2stress[J]. Journal of Atmospheric and Environmental Optics, 2016, 11(1): 51-59. (in Chinese with English abstract)

[21]Endre S, Mayers D F. An Introduction to Numerical Analysis[M]. Cambridge: Cambridge University Press, 2003.

[22]余鹏，孙学金，赵世军. GPS定位中卫星坐标计算的切比雪夫多项式拟合法[J]. 气象科技，2004，32(3)：198，4.

Yu Peng, Sun Xuejin, Zhao Shijun. Chebyshev polynomial fitting method for satellite coordinate calculation in GPS positioning[J]. Meteorological Science and Technology, 2004, 32(3): 198, 4. (in Chinese with English abstract)

[23]任嘉衍，刘慧敏，丁圣彦，等. 伊河流域景观格局变化及其驱动机制[J]. 应用生态学报，2017，28(8)：2611-2620.

Ren Jiayan, Liu Huimin, Ding Shengyan, et al. Changes of landscape pattern in Yi River basin and its driving mechanism[J]. Journal of Applied Ecology, 2017, 28(8): 2611-2620. (in Chinese with English abstract).

[24]于汧卉，杨贵军，王崇倡. 地面高光谱和PROSAIL模型的冬小麦叶绿素反演[J]. 测绘科学，2019，44(11)：96-102.

Yu Qianhui, Yang Guijun, Wang Chongchang. Ground winter wheat chlorophyll of hyperspectral and PROSAIL model inversion[J]. Mapping Science, 2019, 44(11): 96-102. (in Chinese with English abstract).

[25]吴伟斌，李佳雨，张震邦，等. 基于高光谱图像的茶树LAI与氮含量反演[J]. 农业工程学报，2018，34(3)：195-201.

Wu Weibin, Li Jiayu, Zhang Zhenbang, et al. Inversion of tea tree LAI and nitrogen content based on hyperspectral images[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(3): 195-201. (in Chinese with English abstract)

Inversion of winter wheat chlorophyll contents based on improved algorithms for red edge position

Qian Binxiang1,2,3, Huang Wenjiang2,3※, Ye Huichun2,3, Kong Weiping4, Ren Yu1,3, Xing Naichen1,3, Jiao Quanjun2,3

(1100049; 2.,572029,; 3.,100094,; 4.,,100094,)

Red Edge Position (REP) of vegetation spectral reflectance is highly sensitive to chlorophyll content. The inversion model of crop chlorophyll content based on REP enables timely growth monitoring of the crops on a large scale. The displacement of REP and bimodal phenomenon are ubiquitous in 6 traditional algorithms of REP. To reduce the adverse effects effectively, the Newton interpolation method was applied to calculate REP in this study. And two improved REP solving algorithms, Newton-Chebyshev-Node Interpolation (REP_NCNI) and Newton Eight-Point Interpolation (REP_NEPI) were proposed. The strengths and weaknesses of the old and improved algorithms were analyzed, according to the distribution characteristics of REP from different algorithms, and the comprehensive attribute information of the different algorithms was compared. It was found that: 1) Maximum First Derivative (REP_MFD) method and Lagrange Three-Point Interpolation (REP_LAGR) method had the largest variation of REP (41 nm), which was sensitive to chlorophyll content, however, there was an obvious bimodal phenomenon. 2) The REP calculated by an Inverted Gaussian (REP_IG) model method ranged from 695 nm to 729 nm with the lowest mean value (719.5 nm). The whole model moved towards the short-wave direction (blue shift) with the highest Relative Error (RE) (0.882%). 3) The REP calculated by the Linear Four-Point Interpolation method (REP_LFPI) were between 717 and 731 nm, with an average value of 725.4 nm. The whole result was clustered in the direction of a long wave, and the REP had the smallest variation (14 nm), which was not sensitive to the change of chlorophyll content. 4) The variation of the Linear Extrapolation (REP_LE) method was better (39 nm), but the average value was lower (721.9 nm). The whole value moved towards the short-wave direction (blue shift), and the RE was larger (0.551%). 5) The results of polynomial fitting of the ninth order (REP_POLY) were generally good, but the bimodal phenomenon was the most serious. 6) The REP_NCNI and REP_NEPI overcame the bimodal phenomenon and displacement of REP effectively with ideal mean value, amplitude, and RE. And the least square regression was adopted to establish the inversion model of chlorophyll content of winter wheat based on REP. The study revealed that compared with traditionalalgorithms, the improved algorithms exhibited the most accurate and robust performance, where the coefficient of determination of the chlorophyll content inversion model established by improved algorithms was higher than that of traditional algorithms with the coefficient of determination of 0.728 and 0.751, respectively. Moreover, in the improved algorithms, the coefficient of determination between the predicted value and the measured value was greater than 0.619, which was 10.480% higher than that of the REP_MFD method, and the standard root mean square error was less than 0.151, indicating that the goodness of the model was better. At the same time, the coefficient of determination of the inverse equation (0.455-0.758) was higher than that of the fitting equation (0.396-0.656). And the inversion model was ranked chlorophyll-a model, chlorophyll-ab model, and chlorophyll-b model, according to the coefficient of determination from large to small. Besides, the research showed that in the two improved algorithms, the REP_NEPI demonstrated the best and satisfactory performance than REP_NCNI. Considering that only 8 bands were needed to calculate REP by REP_NEPI, it provided a theoretical basis for making a simple sensor to determine the chlorophyll content of crops. The results showed that REP_NEPI was the optimal selection for the calculation of REP and the inversion of chlorophyll content of winter wheat. And this study should provide theoretical and technical support for the inversion of biophysical and biochemical parameters of vegetation and the application in agricultural production.

algorithms; remote sensing; models; winter wheat; inversion of chlorophyll content; Newton-Chebyshev-node interpolation; Newton eight-point interpolation; red edge position

钱彬祥，黄文江，叶回春，等. 红边位置改进算法的冬小麦叶绿素含量反演[J]. 农业工程学报，2020，36(23)：162-170.doi：10.11975/j.issn.1002-6819.2020.23.019 http://www.tcsae.org

Qian Binxiang, Huang Wenjiang, Ye Huichun, et al. Inversion of winter wheat chlorophyll contents based on improved algorithms for red edge position[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(23): 162-170. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.23.019 http://www.tcsae.org

2020-09-24

2020-11-23

国家重点研发计划课题（2016YFD0300601）；国家自然科学基金青年科学基金项目（41871339，41901369）；国家高层次人才特殊支持计划项目（黄文江）

钱彬祥，博士生，主要从事植被定量遥感及应用研究。Email：2789281754@qq.com

黄文江，博士，研究员，博士生导师，主要从事植被定量遥感及应用研究。Email：huangwj@radi.ac.cn

10.11975/j.issn.1002-6819.2020.23.019

S127; S512.1+1

A

1002-6819(2020)-23-0162-09