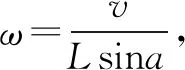速度分解问题的误区跨越

吴远正

(湖北省通山县第二中学 437600)

矢量分解问题中，分解速度是分解力的的后续内容，力、运动的合成和分解在课标和考纲中，都是名符其实的重点知识，也是很多学习困难生的拦路虎，高三一轮复习时可以从以下三个方面突破，跨越误区.

一、遵循分解原则，跨越效果误区

矢量分解的原则是——按实际效果进行分解.速度分解原则同力的分解原则一样，同样按实际效果进行分解，可是力的作用效果与实际运动效果是不一致的，进行速度分解时，很容易受到力的分解方式影响，造成分解错误.

例1湖边工人用水平绳拉小渔船靠岸，如图1所示，工人拉绳匀速向左前行，速度为v，当绳与水面夹角为θ时，求小船的速度是多大？

受力的分解效果干扰，很容易把速度绳子速度v当成力的作用一样进行分解，如图2所示，分解成水平速度vx和竖直速度vy，这样“渔船”变“飞船”，因为小渔船有了向上的速度vy，显然，这是没有把握分解原则，产生是荒谬的分解结果.

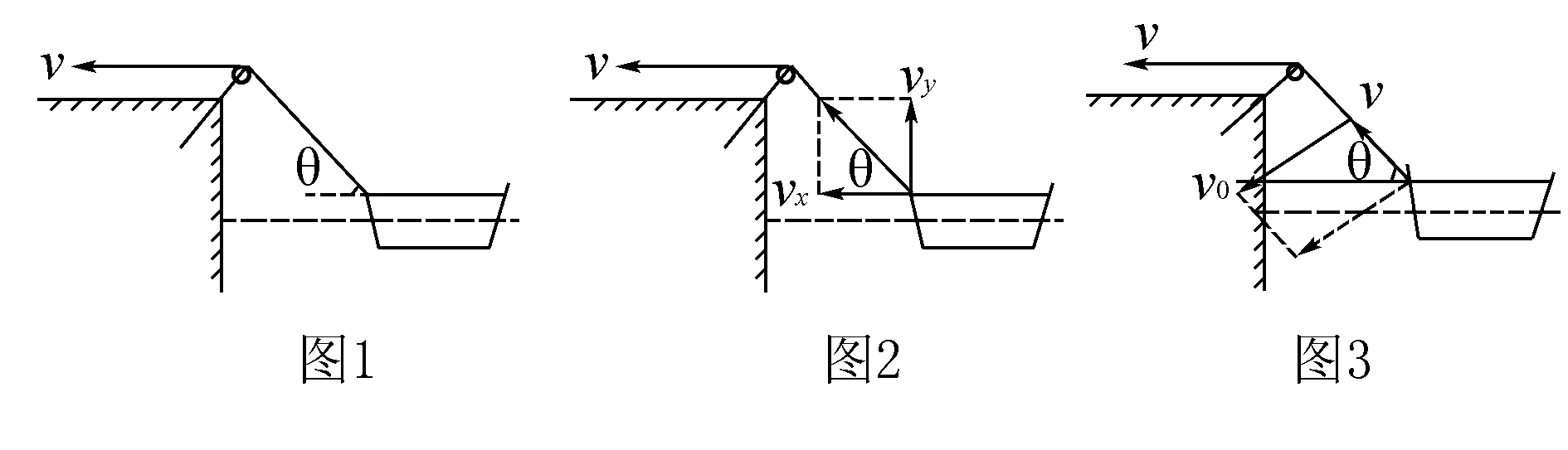
不错，绳子的拉力有水平作用效果和竖直作用效果，而求解小渔船的速度问题时，绳子只是连结实际运动物体的辅件，它的运动始终不是实际运动，小渔船的运动才是实际运动，是小渔船的速度v才是要分解的速度，小渔船向左的运动产生了两个效果，一是沿绳方向收缩运动的效果，二是垂直绳方向摆动绳运动的效果，以小渔船速度v0为平行四边形的对角线，以沿绳方向和垂直绳方向为邻边作平行四边形，这时就方便求得小渔船的速度v0，如图3所示，

二、虚化分解对象，越过实物误区

对于细绳连结的物体，物体的运动才是实际运动，细绳速度始终是分速度，把细绳换成直棒，道理也是一样.

例2如图4所示，平面直角墙壁上有一个直杆，杆上两个端点分别用绞链与A、B两个物块相连，开始时保持装置稳定，开始运动后，物块没有离开接触面，当物块A的速度为v时，杆与竖直墙壁夹角为θ时，求出B物块水平运动的速度.

连接杆如同细绳一样，它的速度也不是实际运动速度，只是A、B两个物体的分速度，这里对A的速度进行分解，A向下滑动有两个效果，使杆子摆动和沿杆方向的运动，设杆的速度为vs，B的水平速度为v1，如图5所示，有

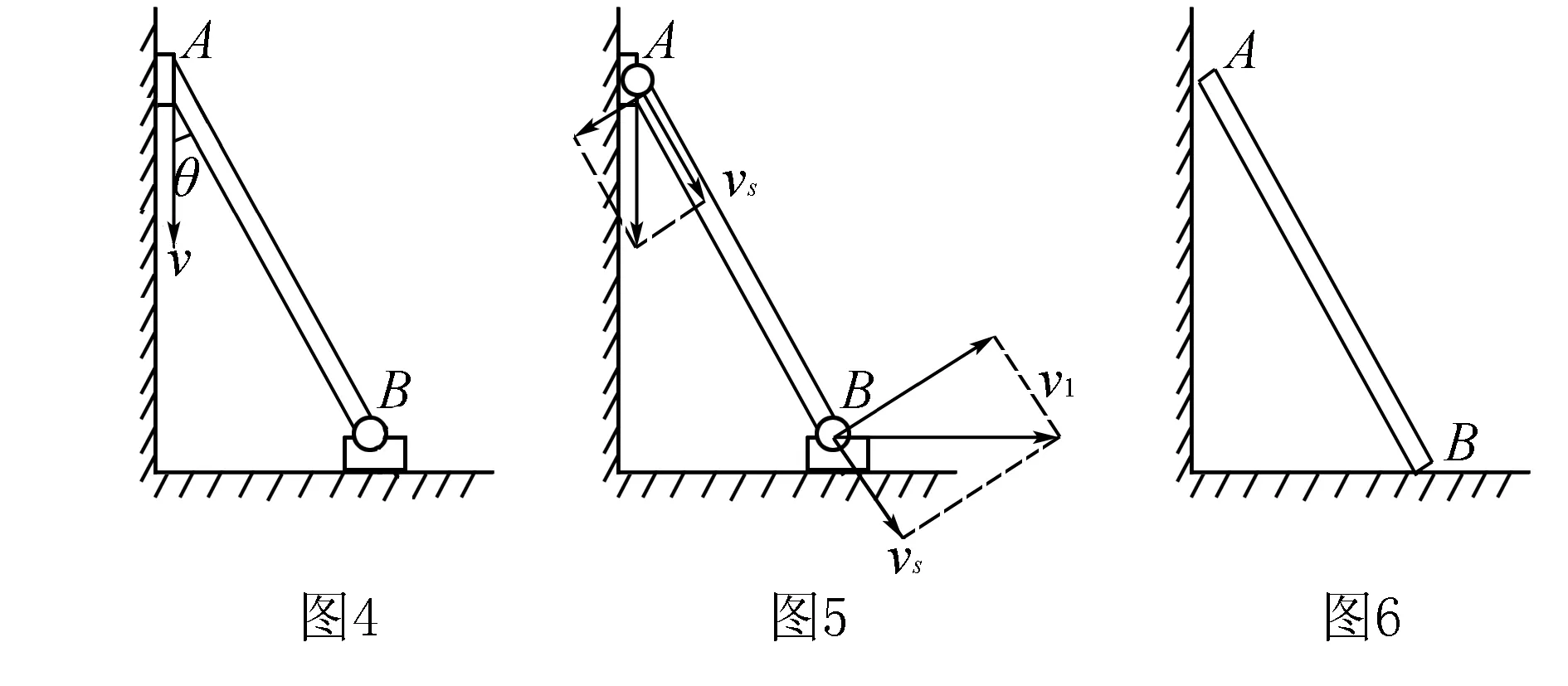
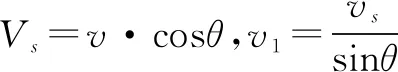
其实，连接A和B两个杆头的速度就是两个物体的速度，这样，当两个物体隐藏后，仅直棒在竖直墙壁上滑动时，如图6所示，两个棒头的速度即为A、B两物体的速度，适应这种实物虚化，直接对直杆进行速度分解，就会减少学生分析题目时的无所适从之感.

三、剖析运动情形，跨越因果误区

分析连接物体的实际运动情形是极为重要的步骤，对分解的速度要经得住推敲、质疑，是合理的分解才会正确，不要受运动因果关系制约，如：

例3如图7所示，长为L的直棒一端可绕固定轴O转动，另一端搁在升降平台上，平台以速度v匀速上升，当棒与竖直方向夹角为a时，棒的角速度为( ).

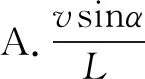
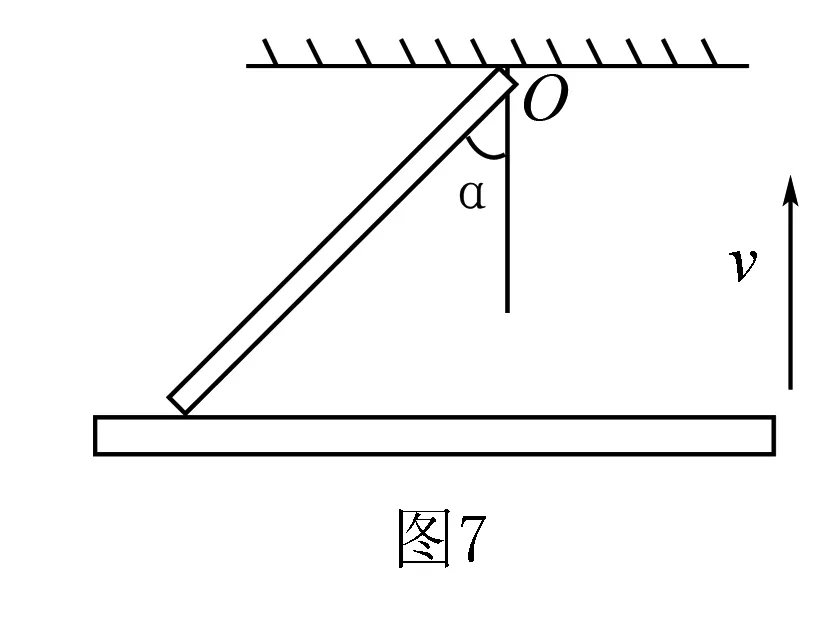
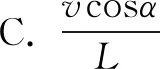
分解谁的运动不好确定，很容易误将平台的速度当成合速度，容易认为平台的运动是因，棒的运动是果.可平台的速度如何分解呢？结合实际情形，平台上升的速度与棒上升的速度是一致的，如果分解该速度，无论如何都找不到v合理的分解结果.

实事上速度分解同运动的因果关系并无关联.这里，棒的上升速度只是棒摆动头速度V0的一个分量，这个V0还有一个效果是使棒向左摆动，所以确定棒的摆动才是合运动，分解棒头摆动的速度才是正解.

棒与平台接触点的实际运动即合运动的速度方向是垂直于棒指向左上方，合速度沿竖直向上的速度分量等于v，