圆锥曲线离心率的取值范围问题的求解方法

武增明

(云南省玉溪第一中学 653100)

求圆锥曲线的离心率的取值范围的问题，是圆锥曲线中的一类重要的问题，这类问题涉及多个知识点，综合性强，解法灵活且多种多样.学生在解答这类问题时，许多同学感到不知从何入手.这类问题主要涉及到函数与方程、数形结合、转化与化归等数学思想方法.解决这类问题的关键是，如何挖掘寻找问题中的不等关系,构造出关于a，b，c的不等式;如何挖掘寻找问题中的变量,建立离心率e关于题设中变量的函数.本文试图通过实例对如何构造出关于a，b，c的不等式和如何建立离心率e关于题设中变量的函数，将问题转化为解关于离心率e的不等式，求以离心率e为函数值的函数的值域问题，作一些归纳、总结、探析，以飨读者.

一、利用圆锥曲线的范围，建立关于a，b，c的不等式

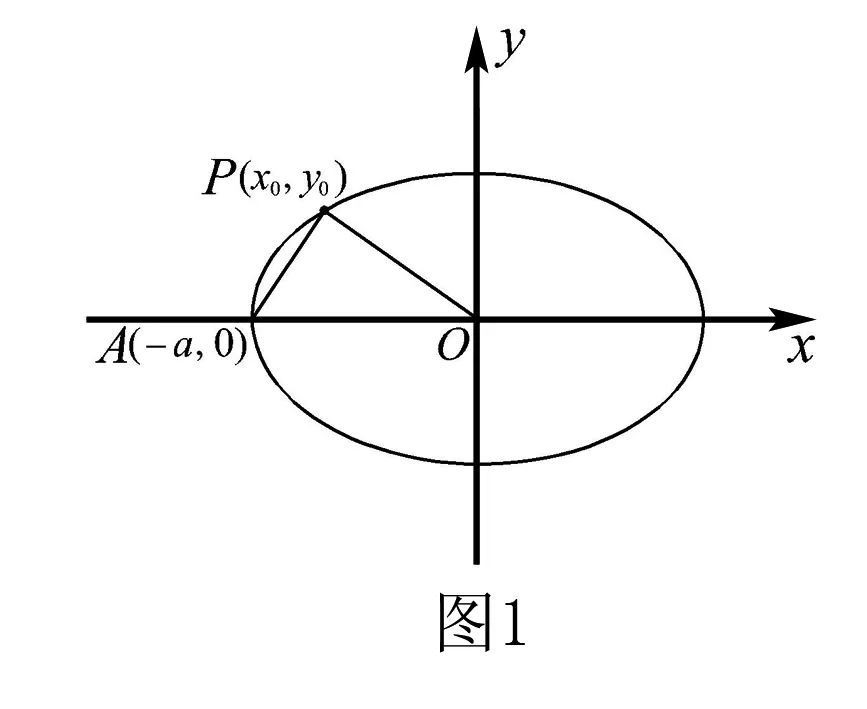
先运用方程思想，用a，b，c表示出圆锥曲线上点的横坐标或纵坐标，然后利用圆锥曲线的范围建立关于a，b，c的不等式，进而转化为关于离心率e的不等式，解此关于离心率e的不等式，问题获解.

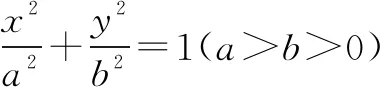
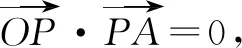
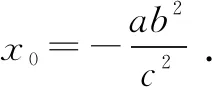
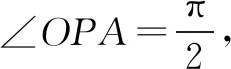
二、利用已知条件中的参数表示出圆锥曲线的离心率，建立函数关系式

先利用已知条件中的参数表示出圆锥曲线的离心率，即将离心率转化为参数的函数，进而将问题转化为求函数的值域问题，然后注意到参数的范围，求出函数的值域，从而问题获解.

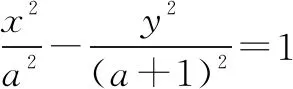
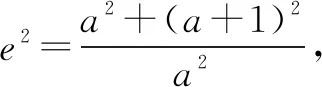
三、利用三角函数的范围，建立关于a，b，c的不等式

先运用方程思想，用a，b，c表示出变量角α的正弦或余弦，然后利用三角函数的范围(有界性)建立关于a，b，c的不等式，进而转化为关于离心率e的不等式，解此关于离心率e的不等式，问题获解.

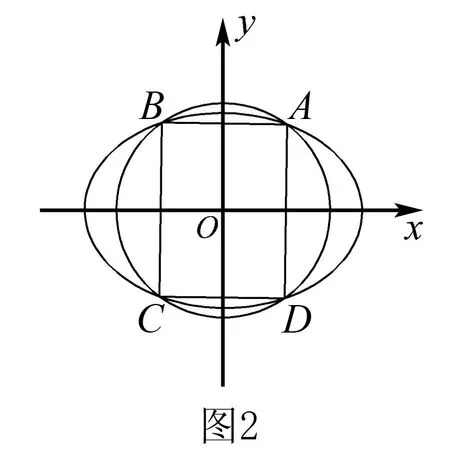
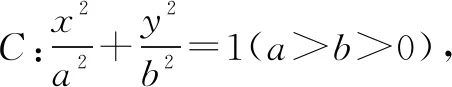
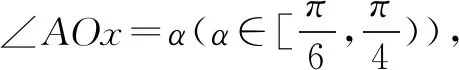
四、利用已知条件中的不等式或范围，建立关于a，b，c的不等式

充分考虑已知条件中的不等式或范围与a，b，c的关系，由此去建立关于a，b，c的不等式，进而转化为关于离心率e的不等式，解此关于离心率e的不等式，问题获解.

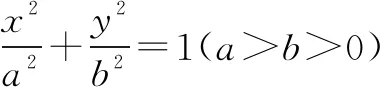
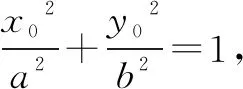
五、利用判别式，建立关于a，b，c的不等式

若直线与圆锥曲线有两个不同的交点，则将直线方程与圆锥曲线方程联立后，判别式大于零，由此建立关于a，b，c的不等式，进而转化为关于离心率e的不等式，解此关于离心率e的不等式，问题获解.

例5斜率为2的直线过中心在原点且焦点在x轴上的双曲线的右焦点，与双曲线的两个交点分别在左、右两支上，则双曲线离心率的取值范围是( ).

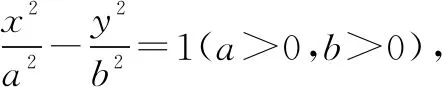
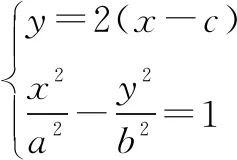
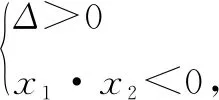
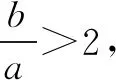
六、利用均值不等式，建立关于a，b，c的不等式

利用均值不等式，建立关于a，b，c的不等式，进而得关于离心率e的不等式，问题获解.

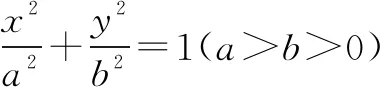
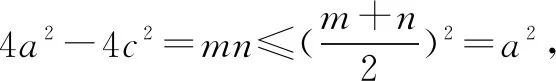
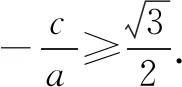
评注解答本题的关键是利用均值不等式，寻找到a，b，c之间的不等关系式，从而获解.

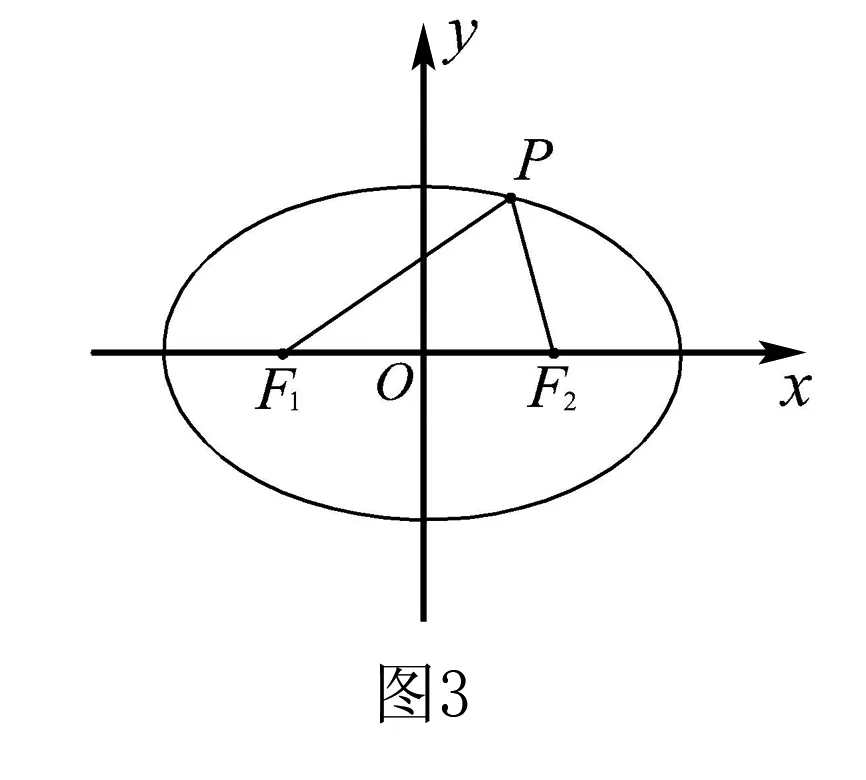
七、利用三角形性质，建立关于a，b，c的不等式

利用三角形任意两边之和大于第三边，任意两边之差小于第三边，同时注意到等号是否会成立，由此建立关于a，b，c的不等式，进而转化为关于离心率e的不等式，解此关于离心率e的不等式，问题获解.

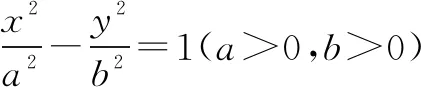
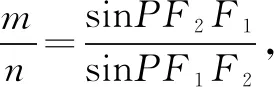
评注根据三角形中恒有“两边之和大于第三边”这一简单的性质，是建立a，b，c之间的不等关系式的关键.

八、利用渐近线的性质，建立关于a，b，c的不等式

利用几何方法、渐近线的几何特性，建立关于a，b，c的不等式，进而转化为离心率e的不等式，解此关于离心率e的不等式，问题获解.

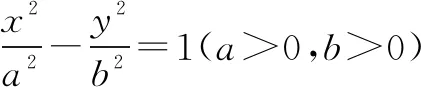
A. (1，2] B. (1，2) C. [2，+∞) D. (2，+∞)

解析此题可以用代数方法求解，即将直线与双曲线方程联立，根据判别式就可确定离心率的取值范围.但计算比较繁琐，因此考虑用几何方法，利用渐近线的几何特性，去求离心率的取值范围.

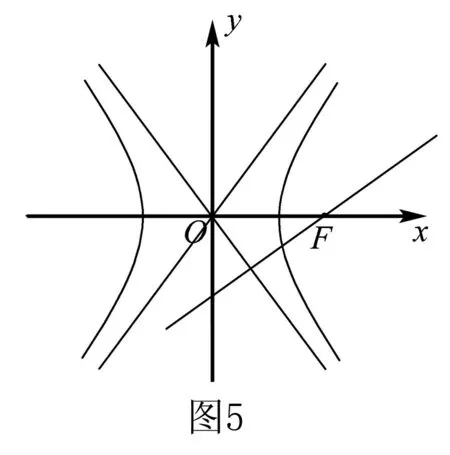
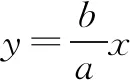
评注渐近线控制着双曲线的形状，这与离心率控制着双曲线的形状有着异曲同工之妙，知道了这点，许多求双曲线离心率的取值范围的问题就可以利用渐近线的性质来很快且轻松地解决了.

圆锥曲线的离心率的取值范围问题的求解方法，并非仅有上面介绍的8种方法，这8种方法仅是基本的、重要的、常见的、常用的方法，除此之外还有数形结合法、参数法等等，并且这些方法并非彼此孤立，在很多时候需要综合运用才能解决问题.限于篇幅，其它方法在此不再赘述，留给读者在学习中探究.但是，若能掌握这8种方法，可以说，解决这类问题就没有问题了.