高中数学选择题的命制方法研究
卢思聪
(福建省平和第一中学 363700)
高考(全国卷)数学科选择题部分的分值占整卷的四成,因此是高中一线数学教师必须潜心研究的课题.这一方面是学生应考的需要,另一方面也是教师更好培养学生数学解题能力的需要.以下从高中数学选择题常见的解题思路来整理阐述命制的技能.
选择题的命制应基于数学知识的内在规律,以数学定义、公式、定理等为基本元素,以数学思想方法为引线来命题.常见的命制方法有:
一、演绎推理法
基于某知识点、某命题,利用简单的逻辑推理来命制选择题的方法,它包含以下几种方法 :
1.直导法
例1依据命题“奇函数图象关于原点对称,偶函数图象关于y轴对称”,可以命制以下选择题:
函数f(x)=x3+x的图象关于 ( ).
A.y轴对称 B.直线y=-x对称
C.原点对称 D.直线y=x对称
从判断函数的奇偶性出发,让学生学会如何判断,从而得到函数图象的对称性.
2.变量替换法
变量替换法是把某些部分看成一个整体,用其它变量代替而生成的新命题,再将新命题构造出数学选择题.
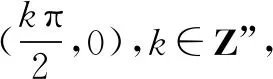
3.逆导法
逆导法是通过联系推导,将已准备的命题隐藏,这种命题的方式叫逆导法.
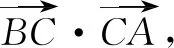
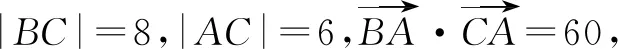
A.150° B.120° C.60° D.30°
二、交换法
寻找某一命题,将该命题的结论和条件交换,它的结论当选择题的条件,由此出发重新命制的方法.它包括:
1.不对等交换
(1)互换位置
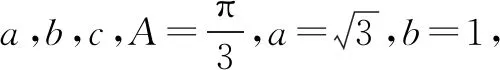
将已知条件b与所求c对调,可以命制以下选择题:
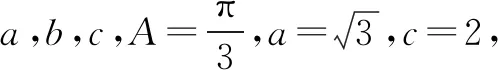
(2)弱化条件法
指的是去除原命题中某些已知条件,或者弱化某些条件,使原题产生质的变化,这种命题方法.
例5原命题:对于任意实数x,一元二次不等式(a-2)x2-2(a-2)x-4<0恒成立,则实数a的取值范围是( ).
A.(-∞,2) B. (-∞,2] C. (-2,2) D. (-2,2]
原命题去除一元二次不等式的限制,可以命制以下选择题:
对于任意实数x,不等式(a-2)x2-2(a-2)x-4<0恒成立,则实数a的取值范围是( ).
A.(-∞,2) B. (-∞,2] C. (-2,2) D. (-2,2]
(3)强化条件法
指的是增加原命题一些限制条件,或者用更好的条件代替原有的部分条件,这种命题方法.
例6原命题:设集合A={x|1 A. ∅ B. (3,4) C.(1,3) D. (1,2)∪(3,4) 原命题增加集合A中的x∈Z限制条件,可以命制以下选择题: 设集合A={x|1 A. ∅ B. (3,4) C.(1,3) D. (1,2)∪(3,4) 2.对等交换 通过等价改变原命题的表达方式,或者等价地更新某个或某些条件,而题目的原有逻辑关系不变,这种命题方法. 也可采用等价的逆否关系的表现形式来命制: 例8原命题:斜率为2的直线经过点A(3,5)、B(a,7)、C(-1,b)三点,则a、b的值为( ). A.a=4,b=0 B.a=-4,b=-3 C.a=4,b=-3 D.a=-4,b=3 采用等价的逆否命题表现形式,可以命制以下选择题: 经过A(3,5)、B(a,7)、C(-1,b)三点的直线,斜率为2,则a、b的值为( ). A.a=4,b=0 B.a=-4,b=-3 C.a=4,b=-3 D.a=-4,b=3 比如:等差(等比)数列具有很多、很好的性质,利用它们相互性质间较强的联系来命制试题. 等差数列{an}的性质:当m+n=p+q时,am+an=ap+aq. 例9已知数列的前n项和为Sn=an2+bn(a,b∈R)且S25=100,则a12+a14为( ). A.16 B.4 C.8 D.不确定 高中数学有些知识块之间形似无关,内容也有很大差异,但其实它们的衔接性、连贯性又能使得离散的知识块有它的内在统一性和逻辑性. 例10已知数列{an}满足a1=1,an=logn(n+1)(n≥2,n∈N*).定义:使乘积a1·a2·a3·…·ak为正整数的k(k∈N*)叫做“和谐数”,则在区间[1,2018]内所有的“和谐数”的和为( ). A.2048 B.4096 C.2036 D.4083 A.{0} B.{1} C.{0,1} D.∅ 在平时教学命题过程中,其实命制方法十分多样,这里无法全部列举.在实际教学实践中,我们可以通过不断的总结整理和积累,解决试卷选择题命制过程中的困惑,从而在试卷命制实践中不断成长. 在整份试卷中,作为客观题部分的选择题,难度其实相对较低,但考点覆盖面却是比较大的,且需要灵活熟练、迅速准确的解题能力.这就要求解题者尽量规避复杂的运算,选择“巧妙”的解答策略,从而快速完成选择.因此在以后的日常教学中,除了引导学生尽量巧做选择题外,在高中选择题的命制上,也力争在不断深入研究探索型和开放型的选择题上有新的成果.
三、知识归纳法
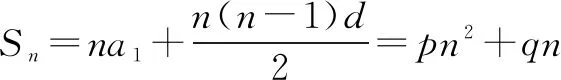
四、考点交叉法