程序框图常见的高考题型例析

杜红全

(甘肃省康县教育局教研室 746500)

算法初步与程序框图是每年高考必考的热点之一，高考命题考查两个方面的内容，一个是基本算法语句，另一个是程序框图，考查均以选择题或填空题的形式出现，试题难度不大，常见的试题类型有两种，下面举例说明.

一、结果输出型

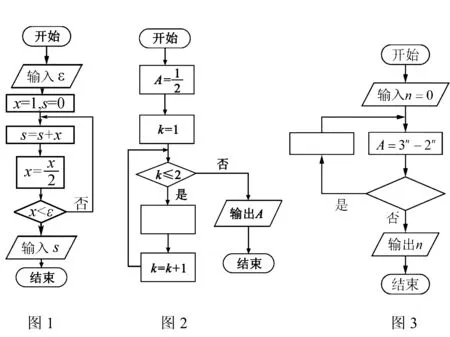
例1(2019年全国Ⅲ，文9理9)执行如图1的程序框图，如果输入的x=1为0.01，则输出x=1的值等于( ).

A.x=1 B.x=1 C.x=1 D.x=1

解析初始值x=1，s=0，执行程序框图.

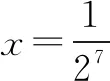
故选C.

点评本题是以程序框图为背景，考查了循环结构的程序框图、等比数列的前n项和公式；命题的形式是给出程序框图和初始数据，求输出结果，即结果输出型；解答本题的关键是准确地看出程序框图的意图，解答本题容易出现两个问题，一是不能准确地判断终止循环的条件，二是求数列的和时不能准确地判断数列的项数.

二、程序框图内条件的完善和补充型

例2 (2019年全国Ⅰ，文9理8)如图2是求A的程序框图，图中空白框中应填入( ).

A．A=AB．A=AC．A=AD．A=A

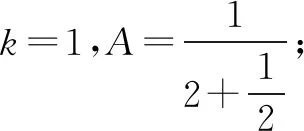
点评本题是以分式的运算为背景，考查循环结构的程序框图；本题是给出框图与输出结果，推理输入的某数据，即完善和补充程序框图; 解决此类问题的关键是读懂循环结构的程序框图，弄清楚当型和直到型循环结构的区别，以及进入、退出循环的条件、循环的次数.

例3 (2017年全国Ⅰ，文10理8)如图3程序框图是为了求出满足3n-2n>1000的最小偶数n，那么在和两个空白框中，可以分别填入( ).

A．A>1000和n=n+1 B.A>1000和n=n+2

C.A≤1000和n=n+1 D.A≤1000和n=n+2

解析因为输出的n为偶数，所以“□”中填n.因为输出的n满足3n-2n>1000，所以◇填A≤1000.故选D.

点评本题巧妙地设置了两个空框需要填写，也是属于完善和补充程序框图；解答本题需要抓住循环的重点、偶数该如何增量；解决此类问题的关键是读懂程序框图，明确顺序结构、条件结构、循环结构的真正含义.

总之，解决识别和完善程序框图需要注意三个问题：首先要明确程序框图的结构，是顺序结构、条件结构，还是循环结构；其次要识别程序框图，明确程序框图的功能；最后看清楚题目的要求，按照程序设计的步骤逐步运行即得结果.