无人机桨叶损伤的在线模型估计新方法

张霄，倪铭，余翔，郭雷

北京航空航天大学 自动化科学与电气工程学院，北京 100083

多旋翼无人机具有垂直起降方便、低空作业灵活等诸多优点，在军事侦察、反恐值勤、电网巡线等军用和民用领域有着广泛的应用[1]。然而无人机在复杂高对抗环境中极易出现结构受损。特别是无人机的桨叶，同时承担着动力输出和控制执行的双重任务。桨叶的损伤将改变无人机的实际控制模型，并严重影响无人机的控制稳定性和飞行安全性。

过去几年中关于无人机桨叶损伤或缺失的相关研究受到越来越多的关注。苏黎世联邦理工学院D’Andrea教授研究团队分别提出了四旋翼无人机缺失1支、2支、3支桨情况下的动力学模型，并进行了相关实验[2-4]。麻省理工学院Annaswamy教授研究团队针对桨叶损伤情况下无人机参数不确定性问题，设计了一种自适应控制器，解决了无人机推力异常情况下的稳定控制问题[5]。加拿大康考迪亚大学Zhang教授团队在文献[6]中总结了故障诊断与容错控制的相关研究，并对四旋翼无人机的执行器和传感器故障进行了建模和相关实验[7]。上述研究均针对确定的多旋翼无人机执行器故障，对于如何应对随机出现的执行器故障并未深入研究。

基于观测器和干扰估计方法是随机故障诊断与表征最常用的方法之一。其基本思想是以测量值为基础，对未知扰动参数进行估计[8-9]。文献[10]针对飞机舵面损伤的快速故障诊断问题,提出一种自适应补偿观测器方法。文献[11]设计了未知输入观测器，用于固定翼无人机的执行机构故障诊断。文献[12]提出了一种基于干扰观测器的反步控制，用于同时估计小型旋翼无人机的外界未知扰动和系统状态。文献[13]针对四旋翼无人机的外界干扰和量测时滞，利用干扰观测器技术实现了对干扰的估计。西班牙加泰罗尼亚理工Puig团队设计了二次型有界观测器，提高了无人机干扰估计速度和估计精度[14]。文献[15]针对四旋翼无人机自主着舰系统，将未知建模动态、地效、状态耦合以及外界干扰等因素看成“集总干扰”进行估计。文献[16]提出了一种基于滑模干扰观测器的控制方法，能够在控制增益和计算量较小的同时保持对外界干扰和模型误差的鲁棒性。文献[17]研究了在扰动参数和外部扰动等条件下四旋翼无人机的控制问题，结合干扰观测器，提出了鲁棒跟踪控制方案。文献[18]针对四旋翼无人机的精确建模和飞行控制问题，提出了一种基于干扰观测器的控制器，将模型的不准确部分和传感器噪声视为干扰并进行抑制。文献[19-20]设计了基于干扰观测器的控制系统，实现了干扰估计与补偿，解决了外界风干扰情况下的旋翼无人机飞行控制问题。上述研究主要针对可观测性较高的外部干扰、未建模内部干扰和内外部集总干扰设计观测器，鲜有文献对多旋翼无人机系统内部干扰的作用形式、量化模型及精细估计问题进行深入研究。

高对抗环境中桨叶的随机损伤引起的干扰是一种存在于控制模型内部、难以直接测量和观测的干扰。针对上述难题，本文拟设计一种新型干扰观测器，通过平行空间映射，提高干扰的可观测性，实现对桨叶随机损伤的快速估计，并在线重建桨叶损伤后的四旋翼无人机动力学模型。

1 桨叶随机损伤动力学模型

在典型四旋翼无人机模型[21]基础上，本节考虑桨叶随机损伤引起的升力损失和扭矩损失，并建立四旋翼无人机动力学模型。

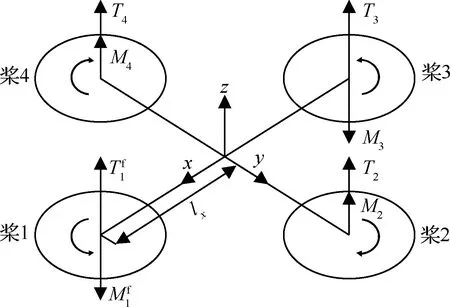
图1 +型构造四旋翼无人机受力分析Fig.1 Force analysis of concerned quadrotor UAV

在图1所示的四旋翼动力学模型中，若螺旋桨1出现损伤，则损伤后螺旋桨1升力可表示为

(1)

式中：CL为螺旋桨标准升力系数;ϖ1为螺旋桨1转速；α为螺旋桨升力的损失比率。

螺旋桨1损伤后对机体的反扭力矩可表示为

(2)

式中:CM为螺旋桨标准扭矩系数;β为螺旋桨扭矩的损失比率。

将螺旋桨桨叶损伤导致的力矩损失量作为系统的扰动力矩d0(t)，则四旋翼无人机在桨叶损伤情况下的动力学模型和运动学模型可表示为

(3)

在上述桨叶损伤模型条件下，四旋翼机体所受升力和力矩模型发生变化，如图1所示，当螺旋桨1损伤时，机体所受升力和力矩为

(4)

具体可表示为

(5)

式中：ϖi(i=1,2,3,4)为对应序号螺旋桨转速。

此时，桨叶损伤产生的扰动力矩d0(t)可表示为

(6)

对于损伤桨叶动力学模型的在线重建，关键便是对干扰d0(t)进行观测和估计。

2 穿透型干扰观测器

桨叶的随机损伤干扰d0存在于模型内部，可观测性较低。典型的干扰观测器难以实现对此类干扰的观测和估计。为了解决此类干扰的观测问题，本文提出一种“穿透函数”观测方法。穿透函数将模型内部的干扰映射到一个新建的平行空间中，在平行空间中通过设计相应的干扰观测器，可实现对此类干扰的观测和估计。本文将这种新型的干扰器称为穿透型干扰观测器(Penetrating Disturbance Observer，PDO)。穿透型干扰观测器的结构框图如图2所示。

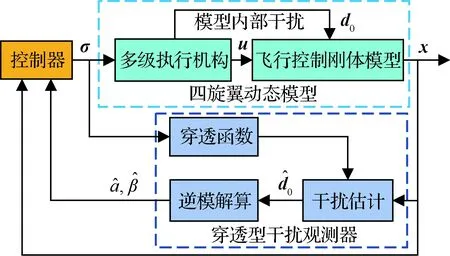
图2 穿透型干扰观测器结构框图Fig.2 Structure diagram of PDO

对式(3)表示的四旋翼姿态非线性模型进行线性化，得到四旋翼姿态线性模型，在螺旋桨桨叶损伤情况下，构造机体姿态控制系统状态方程为

(7)

选择状态变量为

(8)

控制输入变量为

u(t)=τ=[τx,τy,τz]T

(9)

则状态方程中

(10)

对上述线性系统中存在的干扰d0(t)设计穿透型干扰观测器：

(11)

式中：P0为所构造的干扰观测器穿透函数；σ(t)为控制器输出指令σ(t)=[σ1,σ2,σ3,σ4]T。

四旋翼无人机实际系统中，多级执行机构施加在系统动力学模型上的力或力矩u(t)难以通过传感器进行直接测量。尤其是在四旋翼无人机桨叶随机损伤故障下，多级执行机构产生的力矩输出u(t)叠加桨叶损伤产生的系统内部干扰d0(t)，更加难以分离出u(t)，给干扰观测器的设计造成了较大困难。因此，在设计穿透型干扰观测器(11)时，以可测量的P0σ(t)替代了传统干扰观测器中的u(t)，并将P0σ(t)作为穿透型干扰观测器(11)的输入项，有效解决了四旋翼无人机桨叶随机损伤故障下力矩输入u(t)难以直接测量的问题。

假设所构造干扰观测器穿透函数P0可以准确反映控制器输出至飞行控制刚体模型间的多级执行机构系统模型，即满足：

P0σ(t)=u(t)

(12)

定义干扰观测器估计误差为

(13)

结合式(7)、式(11)、式(12)，可得

(14)

因此，当观测器增益矩阵L满足：LH=S为Hurwitz矩阵条件时，穿透型干扰观测器(11)估计误差渐近稳定[22]。

将干扰表征为

(15)

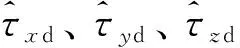
穿透型干扰观测器的输出是机体各轴向的力矩干扰量的估计值，为了获得螺旋桨损伤后的模型参数，需要根据力矩干扰量逆模型进行反演解算出损伤模型参数，反演解算方式为

(16)

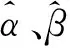
3 实验验证

3.1 实验环境

为了验证穿透型干扰观测器的性能，构建了图3所示的四旋翼无人机半物理仿真系统。系统由四旋翼无人机、动力部件参数测量装置、数据采集与仿真计算机、自动驾驶仪4个部分组成。飞行控制刚体动力学模型参数采用四旋翼无人机实际测量数据。动力部件参数测量装置用于测量驱动电机和桨叶的相关参数。数据采集与仿真计算机用于采集无人机相关参数及实时状态。自动驾驶仪用于实现无人机实时控制信号的加载。半物理仿真实验系统测量参数结果如表1所示。

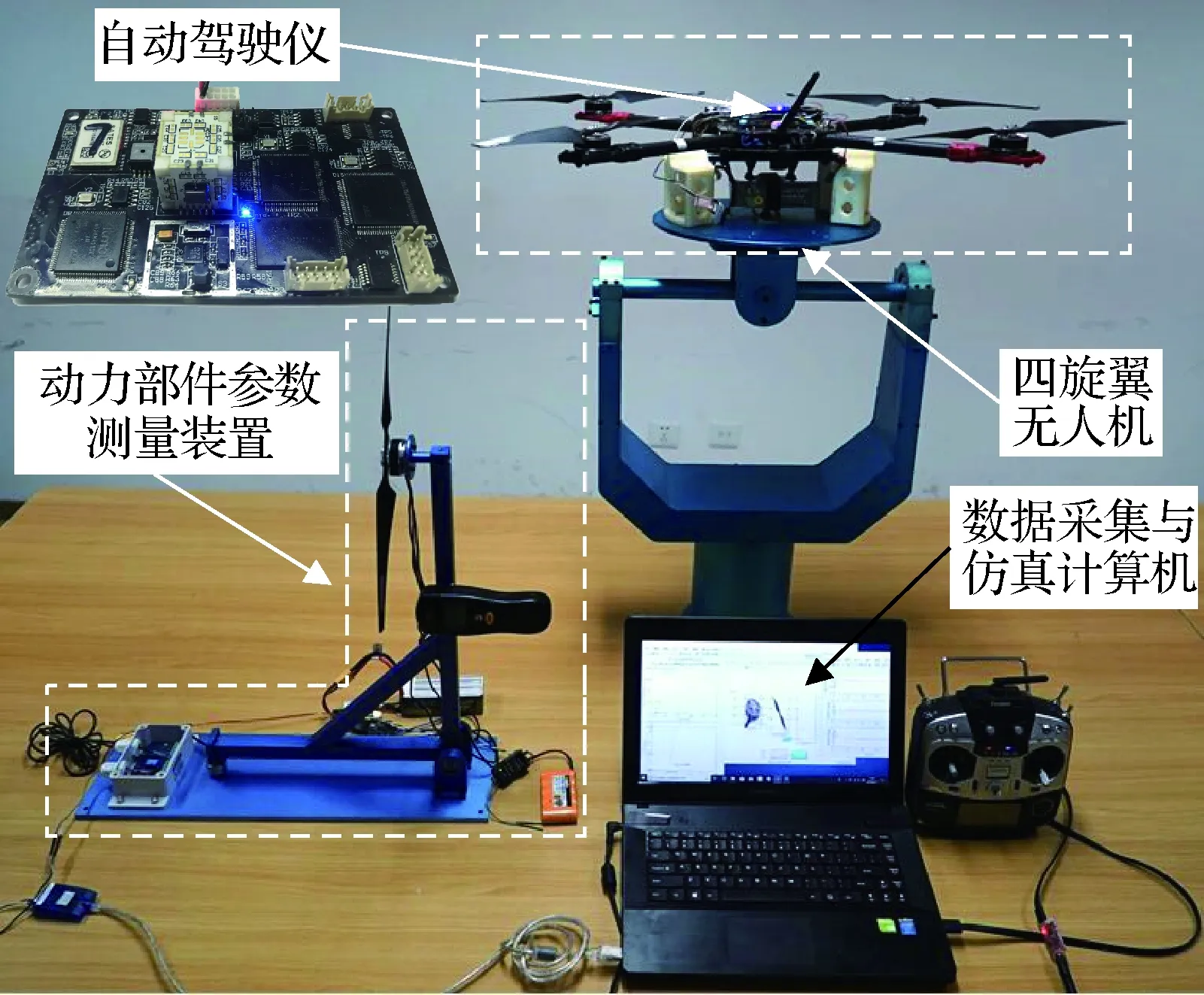
图3 四旋翼无人机半物理仿真实验系统Fig.3 Quadrotor UAV semi-physical simulation experiment system

表1 四旋翼无人机参数测量结果Table 1 Quadrotor UAV parameter measurement results

干扰观测器穿透函数P0的构造方式为

(17)

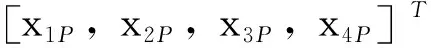
在式(17)中构造了4组无刷直流电机串联螺旋桨模型，并将表1中的参数测量结果代入，可较为准确地反映四旋翼无人机控制输入至飞行控制刚体模型间的多级执行机构系统模型，使最终通过穿透函数计算获得的力矩输出τP=P0σ(t)=u(t)，且不包含桨叶损伤故障产生的系统内部干扰d0(t)，从而满足条件(12)。

取观测器增益矩阵为

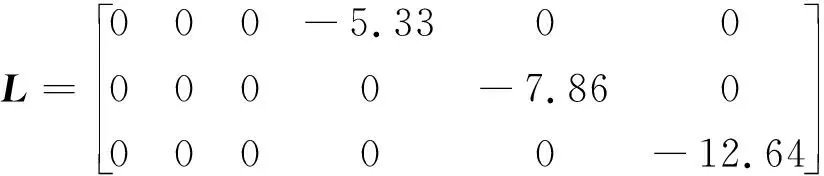
3.2 模拟桨叶损伤参数测试实验

在实验中，人为破坏图1所示的四旋翼无人机的1号桨模拟桨叶损失。动力部件动力学模型测量装置采集数据经地面站平台分析可得桨叶损伤参数测试结果如图4所示。

图4 桨叶损伤前后参数测试结果Fig.4 Parameter test results before and after blade damage

实验表明损伤后相同转速下螺旋桨升力和反扭力矩均下降，但升力和转速的平方、反扭力矩和转速的平方依然满足线性关系，升力损失比率α=0.193 5，扭矩损失比率β=0.266 5。

3.3 损伤参数估计与姿态控制仿真实验

进行PID和PID+PDO控制方法无人机姿态仿真对比实验，故障发生前后2种控制器参数均保持不变。实验结果如图6所示。

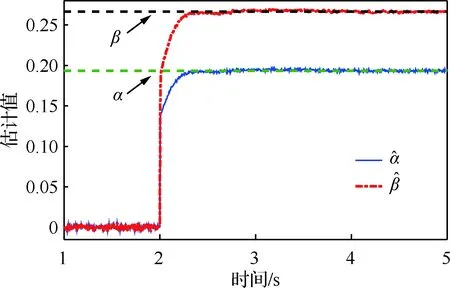
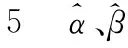
图估计曲线Fig.5 Estimation curves of

图6 姿态曲线Fig.6 Attitude curves

仿真结果表明，采用PID+PDO方法可在不改变所用控制器参数条件下显著减小桨叶出现随机损伤瞬间的姿态角振幅，加快姿态稳定速度，故障发生3 s后水平姿态稳定归零。并有效消除后续机体振荡现象和姿态稳态误差，显著提高姿态稳定性能。控制指标对比如图7所示，损伤瞬间横滚角、俯仰角、偏航角振幅分别减少85.5%、45%、58.9%，俯仰角、偏航角稳态误差分别减少99.6%、68.4%。

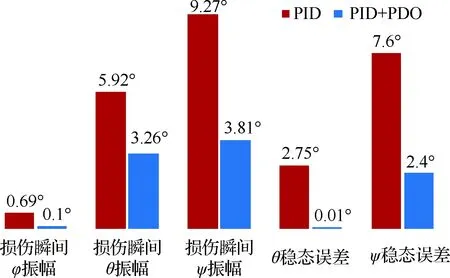
图7 姿态控制指标对比Fig.7 Comparison of flight attitude indicators

4 结 论

1) 本文提出的穿透型干扰观测器，其核心在于穿透函数的设计。穿透函数与控制对象的匹配性是保证穿透型干扰观测器稳定和准确的基本条件。

2) 四旋翼无人机桨叶的损伤属于随机干扰。有利于穿透函数的设计，干扰观测器快速实现了对桨叶损伤随机干扰的实时估计。

穿透型干扰观测器结构中，控制器的设计对于干扰估计的速度和精度同样具有较大的影响。下一步可考虑设计其他具有收敛速度优势的控制器，进一步提升干扰观测的响应速度。