单孔容腔瞬态充气换热的理论分析方法
丁水汀,于航,邱天,*,单晓明,贺宜红
1. 北京航空航天大学 能源与动力工程学院,北京 100083 2. 北京航空航天大学 航空发动机气动热力国家重点实验室,北京 100083 3. 中国航发湖南动力机械研究所,株洲 412000
伴随对航空发动机性能需求的不断提高及航空发动机技术的快速发展,发动机强整体、强瞬变、强耦合、强非线性的特征愈发凸显。发动机运行状态复杂多变,对发动机的安全性造成隐患。现阶段,航空发动机尤其是军用飞机发动机在整个飞行剖面内大部分处于多变的运行环境中,发动机经历慢车到最大转速的时间缩短,瞬变特征显著,严苛的运行条件导致发动机在过渡过程中故障频发[1]。
航空发动机是一多系统协调工作的实体,其中空气系统是处于发动机主流道内侧、外侧的转子与静子或转静子之间联系不同腔室、间隙、孔缝的空气系统流路总称[2],具有发动机冷却、封严、轴向力控制等重要作用。腔室类元件由于自身质量和能量的存储和释放效应而具有显著的瞬态特征,在发动机过渡过程中起到至关重要的作用。从压气机引气的气流边界发生变化时,各腔室的压力变化存在滞后性,对压力变化的预测直接影响到推算发动机轴向力的动态变化。这一指标在发动机安全性设计中有明确规定:发动机压力平衡系统需提供合适的轴向载荷[3]。
为预测容腔压力瞬态变化,已开展大量关于容腔瞬态响应规律的研究。Dutton和Coverdill[4]通过试验研究了容腔充放气过程,定性分析了描述瞬态变化的两种理论模型(绝热模型和等温模型)基本假设的适用条件,并使用这两种理论模型预测容腔的压力变化。通过与试验结果进行比较,发现模型与试验数据间存在差异,但是文中没有针对真实响应过程提出更为精确的数值模型。Thorncroft等[5]认为容腔瞬态响应是一多变过程,通过试验修正了多变过程的多变指数,使模拟结果与试验数据吻合。这一结果也表明了响应过程为非确定过程,非绝热也非等温,但只针对特定的试验数据进行模型修正,不具有可拓展性。Gallar和Calcagni[6]描述了静止容腔瞬态响应的数学模型,并借助此模型进行了空气系统网络的建模与分析工作。
在工程上,普遍采用绝热假设,即不考虑瞬态过程中气体与腔壁的换热,基于该方法模拟的压力响应过程与实际存在较大差别[4-7]。另一种较常采用的是等温假设,即在瞬态过程中气体温度始终保持不变[4],这种方法过高地估计了换热作用。两种方法的模拟精度都较差,根本原因在于缺少分析瞬态换热过程的有效方法。为了提高模拟精度,许多学者开展了针对容腔瞬态换热的研究。杨丽红等[8]研究了换热效应对于等温容腔放气过程的影响。郭钟华等[9]则针对真空系统容腔的压力响应建立了考虑换热影响的真空抽吸模型,使用了定努塞尔数换热模型,较好地模拟了真实响应过程。但是瞬态过程流动与换热状态随时间变化,换热分析方法应能适应变工况变化。本文作者团队[10-11]针对非绝热容腔瞬态响应过程进行了建模与试验研究,给出了通用的换热特性准则式,提出了一种研究瞬态换热的可行方法。
目前,开展容腔瞬态换热分析的试验成本和CFD模拟成本都很高,若利用绝热模型和等温模型简化计算,模拟精度又较低。所以,本文提出了一种具有较高精度,且可以大幅降低成本的理论方法。以非绝热单孔立方体容腔为研究对象,从容腔大间距冲击流动和外掠平板换热理论出发,建立了容腔瞬态换热的理论分析方法,并对方法进行了试验验证。
1 理论分析方法
在容腔充气过程中,由于发生质量和能量存储的时间尺度远大于建立稳定流场的时间尺度,所以认为在瞬态过程中的任一时刻,流动与换热仅与当前进气流动参数和腔内气体状态参数有关,与瞬变过程无关,基于这一假设建立瞬态换热的理论分析方法。
首先,需明确容腔充气的物理过程。立方体容腔中心横截面上的充气流动结构如图1所示,气流自圆形喷嘴射出,射流主要流经3个明显的流动区域,即自由射流区、冲击区和壁面射流区。在自由射流区,流动特性与自由射流相同,在冲击区,气流冲击壁面并在所有方向上均匀地沿径向扩散,气流经历了显著的弯曲,在该区末形成平行于壁面的流动,进入到壁面射流区,随后气流撞击到侧壁面继续流动,最终在容腔内形成循环流动。
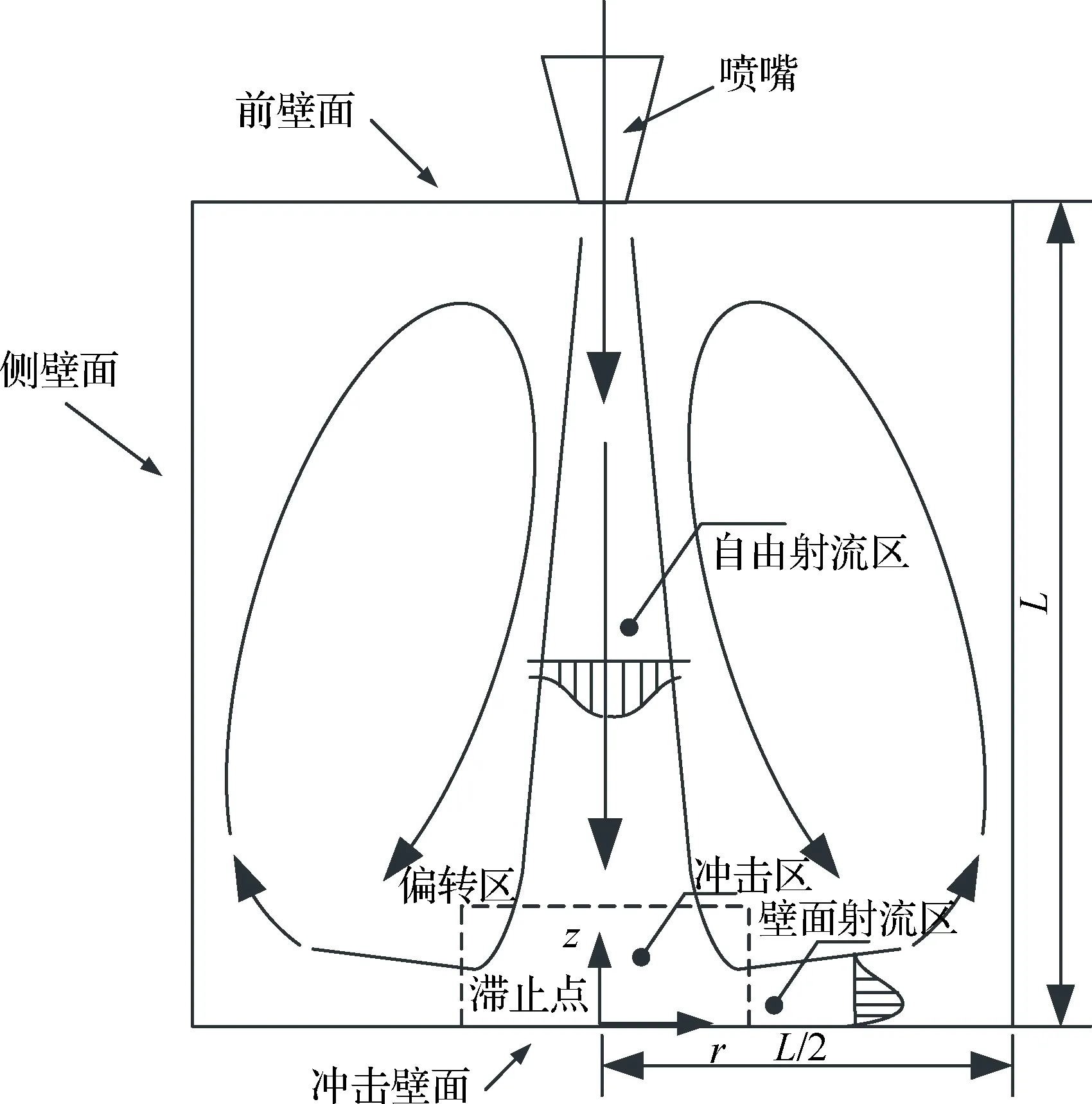
图1 容腔中心截面充气流动结构Fig.1 Charging flow structure of cavity central section
对于容腔这类大间距冲击射流结构,且喷嘴截面积远小于容腔截面积,喷嘴出口射流受侧壁及前壁影响较小,可近似为自由射流(除紧邻冲击壁面的位置)。以冲击壁面滞止点为原点建立圆柱坐标系,图1中纵轴为冲击壁面法向z轴,横轴为径向r轴,自由射流轴向速度满足[12]
(1)
式中:uz为轴向速度;u0为射流速度,在充气过程中,随着容腔内气体压力的逐渐升高而减小;d为圆形喷嘴喉道直径;z为距冲击壁面的法向距离;L为喷嘴出口到冲击壁面的距离。式(1)在自由射流处于充分发展段适用,通常在(L-z)/d>40范围内自由射流处于充分发展,各断面的流速分布具有相似性。同时为了保证射流外部对射流发展没有影响,要求侧壁尽量远离射流,需满足R/d≫1,R为侧壁距射流中心的距离。当z/L≥0.05时,uz/u0随d/(L-z)线性变化,可用自由射流轴向速度的变化关系式(1)描述。在冲击滞止点处,速度为0。对于三维轴对称无摩擦流,滞止点附近的轴向速度[13]为
uz=-2az
(2)
径向速度为
ur=ar
(3)
式中:a为常数;r为径向距离。当z/L≤0.05时,冲击射流轴向速度落在滞止点附近的线性变化区[14],取z/L=0.05位置处的速度u0.05作为线性变化区的特征速度,则根据式(2),常数a为
(4)
气流冲击到滞止点产生高压区,诱使滞止点临近区域流动为层流[13]。首先定义无量纲温度θ=(T-T∞)/(Tw-T∞),其中,T∞为热边界层外层流体温度,Tw为壁面温度,则层流热边界层内温度型[15]可表示为
(5)
式中:δt为热边界层厚度。壁面换热热流密度为
(6)
其中:λ为导热系数。利用无量纲温度分布,式(6)可简化为
(7)
对流换热系数为
(8)
基于上述分析,通过求解热边界层厚度δt即可求得对流换热系数。轴对称、定常圆柱坐标系下的连续性方程及忽略黏性耗散的能量方程分别为
(9)
(10)
式中:α为热扩散系数。
假设热边界层内沿流向传递的热流大小远小于沿壁面法向传递的热流大小,即
(11)
则式(10)可简化为
(12)
沿壁面法向0~δt对式(12)进行积分,以无量纲温度表示为
(13)
又有
(14)
(15)
将边界条件代入,式(13)可化为
(16)
联立式(9),得
(17)
将式(3)和式(5)代入式(17),则有
(18)
式(18)的推导是基于滞止点区域的热边界层厚度与径向位置无关的结论[16]。又由式(5),可得
(19)
联立式(18)和式(19),得
(20)
代入式(8),则冲击壁面滞止点对流换热系数hs为
(21)
文献[17]在分析中指出冲击区内换热努塞尔数与偏离滞止点的距离无关,故认为整个冲击区域内对流换热系数相同。
气流冲击到壁面后,径向速度从滞止点处零先达到峰值,随后由于能量耗散及壁面阻碍减速,气体由冲击区流入到壁面射流区,流动状态已由层流转捩为湍流[18-19]。文献[14]指出冲击射流壁面射流区范围为r/L>0.22时,壁面射流区速度衰减规律[20]为
(22)
式中:K为冲击射流的动量通量。
恒定均匀壁面温度条件下流体外掠平板湍流换热局部努塞尔数[15]为
(23)

(24)

(25)
冲击壁面换热热流密度为
(26)
式中:Tv为容腔内气体温度。
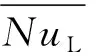

(27)



(28)
至此,容腔瞬态充气过程各壁面的换热热流均得到确定。上述建立的方法需满足一定的几何条件,具体为自由射流应处于充分发展,满足(L-z)/d>40;侧壁距射流中心足够远,满足R/d≫1。同时,方法中所采用的经验关系式均经过大量的理论或试验验证,在冲击射流领域普遍使用,具有可信度。
以各壁面热流总和作为容腔零维瞬态模型能量方程中的热流输入,模拟压力和温度的瞬态响应过程。具体的建模方法见文献[11]。
2 方法验证及讨论
通过容腔瞬态充气试验对理论方法进行验证。利用试验获取容腔瞬态充气过程中压力及温度的响应历程,与基于瞬态换热理论分析方法的零维模型模拟结果进行对比,验证方法的可行性。
2.1 试验方法
容腔瞬态充气试验在静止容腔试验台上进行,试验台如图2所示,其中包括了稳压箱、容腔试验件、数据采集系统等。

图2 静止容腔试验台示意图Fig.2 Schematic diagram of static cavity experimental apparatus
此前,本文作者团队通过瞬态充气换热试验获得了单一进气喷嘴、不同恒定壁面温度条件下的容腔瞬态响应规律,分析了相应条件下的瞬态换热特性[10]。但是本文建立的理论方法的可行性及通用性主要受容腔无量纲冲击距的影响,受壁面温度影响不大。所以,为改变无量纲冲击距,在该试验台的基础上,不改变容腔的几何尺寸,只更换充气喷嘴,进行了多组不同喉道直径喷嘴的容腔瞬态充气试验。
试验装置整体结构及几何尺寸如图3所示,试验件是立方体容腔,采用金属铝制成,内边长为300 mm,厚度为50 mm,实物如图4所示。包裹喷嘴管壁外侧的聚氨酯环用于密封及防止腔壁与喷嘴管壁间传热,外层岩棉为隔热材料。

图3 试验装置Fig.3 Experimental apparatus

图4 容腔实物图Fig.4 Photograph of cavity
配备4种不同的渐缩喷嘴,喉道直径分别为3.4、5.0、7.0、9.0 mm,实物如图5所示。

图5 渐缩喷嘴实物图Fig.5 Photograph of converging nozzle
容腔壁面上布置了3个压力测点,容腔内布置了3个温度测点,压力传感器与容腔内壁面齐平安装,热电偶伸入容腔内部,分别布置在立方体容腔3个顶点附近,该位置与相邻的3个内壁面距离相同,均为35 mm,具体位置如图6所示。同时,在进气位置上游布置了压力和温度测点用于监测进气边界条件。其中,供气温度是通过布置在气动阀门前30 mm左右位置处的热电偶测试,测点距离喷嘴喉道位置约400 mm。试验开始前,气体处于静止状态,测得的温度为气体总温。对于容腔内气体温度的判定关注的是供气总温,因为对于特定气体,总温就代表了总能量。试验过程中供气温度与环境温度相同,气流流经阀门及喷嘴时,在喷嘴中加速膨胀,此过程中气体温度会略低于喷嘴管壁。但是由于流动过程迅速,在喷嘴中气体与外界基本无换热,可以看作是绝能流动,总温不变,故忽略了气体在喷嘴中的温度变化,认为供气温度与测点位置处温度相同。

图6 测点布置Fig.6 Locations of measurement points
2.2 结果对比与分析
试验进气压力为310 560 Pa,进气温度为298.0 K,容腔壁面热边界为恒温334.0 K(边界的实现见文献[10]),腔内气体初始压力为大气压,初始温度与壁面温度相同。喷嘴喉道直径分别为3.4、5.0、7.0、9.0 mm的试验数据与理论非绝热模型(基于换热理论分析方法)、绝热模型及等温模型的计算结果对比如图7所示。当容腔内气体压力达到进气压力时,充气试验过程结束。
从图7中可以看出,压力及温度的试验瞬态响应与理论非绝热模型计算结果吻合很好,压力最大相对误差不超过3%,温度最大相对误差不超过1%。绝热模型与试验数据相比,压力和温度的最大相对误差分别为12%和14%。等温模型与试验数据相比,压力和温度的最大相对误差分别为6%和7%。事实上,绝热模型和等温模型是两种极限模型,分别忽略了换热效应和极大地估计了换热效应。在容腔充气过程中,压力和温度的实际响应过程介于两种模型之间。
从压力瞬态响应规律可以看出:① 随着充气过程的进行,气体压力逐渐升高,最后稳定,稳定腔压等于进气压力;② 不同喷嘴喉道直径条件下的瞬态响应快慢不同,喉道直径越大,充气流量越大,响应时间越短;③ 随着喷嘴喉道直径的增大,压力瞬态响应更接近绝热模型,偏离等温模型。喉道直径大意味着充气流量大,即进气焓流量大,转化为储存的气体内能多,引起气体温升大,等壁温条件下换热热流密度大。虽然换热热流大,但是瞬态响应过程更接近绝热模型,偏离等温模型。判断响应过程更符合哪种假设,不是以换热热流的大小为判断依据,而是以进气焓流与换热热流之比作为依据。在喷嘴喉道直径大的条件下,进气焓流与换热热流之比更大,所以能量较多地储存在容腔中,响应过程也更接近绝热模型。


图7 不同喷嘴条件下试验、理论非绝热模型、绝热模型及等温模型结果对比Fig.7 Result comparisons of experiment, theoretical non-adiabatic model, adiabatic model, and isothermal model with different nozzles
从温度瞬态响应规律可以看出:① 随着充气过程的进行,气体温度先升高,后缓慢下降。初始时刻,进气焓流要大于壁面换热热流,进气焓更多地转化为气体内能,导致温度升高。随着壁面换热增强,当进气焓流与换热热流之比小于1时,温度开始下降。② 在绝热模型中,进气焓全部转化为气体内能储存在容腔中,模拟的温度持续上升,背离真实变化趋势。③ 随着喷嘴喉道直径的增大,温度升高过程中达到的峰值越大。随着喷嘴喉道直径的减小,温度下降的趋势则更明显。从前面的分析知道,喉道直径小响应规律偏离绝热模型,接近等温模型,气体温升小,换热热流小。虽然小喉道直径下换热热流小,但是在温升阶段,小温升导致的气体内能增量也偏少,两者综合作用导致温度下降的趋势更明显。
3 结 论
本文基于自由射流、冲击射流及流体外掠平板换热等理论,建立了分析容腔瞬态充气换热的理论方法,模拟了非绝热单孔容腔瞬态充气过程的压力和温度变化,并通过试验进行了验证。主要结论为
1) 对容腔瞬态充气过程换热的理论分析方法进行了研究,并基于理论方法模拟了容腔压力及温度的瞬态响应过程。模拟结果与试验数据吻合很好,其中压力最大相对误差不超过3%,温度最大相对误差不超过1%,验证了该方法的可行性及准确性。
2) 在相同的物理边界条件下,喷嘴喉道直径越大,充气过程越接近绝热模型,偏离等温模型,响应速度越快。
3) 相较于绝热模型或等温模型,利用该理论方法不仅提高了模拟精度,而且分析方法更具通用性。将封闭容腔内部流动抽象为基本的自由射流、冲击射流、壁面射流及外掠平板流动单元的组合,该方法适用于具有这类相似流动结构的换热分析。虽然抽象结构与真实流动存在差异,牺牲了一定精度,但提高了方法的可拓展性,使其具备了解决相似问题的能力。同时,理论方法对于研究空气系统容腔类元件的瞬态换热具有一定的指导意义。

