复杂结冰环境下飞机鲁棒飞行安全包线分析

禹志龙，李颖晖，郑无计，徐文丰，董泽洪

空军工程大学 航空工程学院，西安 710038

飞机结冰是飞行实践中广泛存在的一种物理现象[1]，通常会破坏飞机的动力学特性，影响飞机的操稳性特性，降低飞行品质，严重威胁飞机飞行安全[2]。自20世纪20年代以来，飞机结冰一直是威胁航空安全的重要问题[3]，美国Safety Advisor对1990—2000年间因气象原因造成的飞行事故进行统计，共有3 230起，其中结冰事故占12%[4]，随后在2003—2008年间，又发生了380起因为结冰导致的飞行事故。

针对结冰对飞行安全造成的威胁，国外学者从20世纪30年代开始对结冰现象进行研究。Lynch和Khodadoust深入系统地研究了不同结冰位置、结冰形状对飞机升、阻力系数的影响，并量化分析了结冰引起的气动特性变化[5]。Bragg和Basar在国际结冰会议上提出了进行结冰程度量化的模型[6]，为结冰的量化分析奠定了基础。国内以研究飞机结冰、防除冰机理[7], 操纵保护，风险量化、评估[8]为重点。

为了降低飞机在结冰条件下的飞行风险，必须建立飞机的飞行安全包线，而传统飞行安全包线保护通常只用于防止飞行员操纵飞机进入超出飞机结构和气动极限的状态。1994年，美国鹰航公司一架ATR72-212飞机坠毁于印第安纳州，当时飞机的飞行迎角仅为5°，远低于飞控系统提供的迎角限制值18.1°，可是在机翼结冰的影响下，飞机仍然因失速而导致坠毁[9]。因此，必须获得飞机在复杂结冰环境下的飞行安全包线。目前，国内外确定飞行安全包线的方法很多，其中获得广大研究者公认的方法之一就是可达性分析[10]。可达性分析是指针对微分动力系统，是否可以通过有效控制策略、在特定的时间范围内使初始集范围内的状态达到指定目标集合的过程。该方法应用范围较广，在航空领域安全分析中表现突出。文献[11]利用可达集方法计算了飞机着陆阶段的飞行安全包线，并分析了襟翼切换对于飞机着陆时飞行安全包线的影响，文献[12]以最大可控不变集作为飞机的安全集，并基于安全集研究了机动边界的保护控制，文献[13]基于可达集方法求解飞行器筋斗动作各阶段的操纵边界，为飞行员完成标准动作提供决策支撑。由于可达集理论的实用性，一些学者将可达集理论应于对结冰飞行安全的研究，文献[14-15]将可达集用于结冰飞机着陆阶段的飞行安全研究，并分别得出不同结冰程度下的飞行风险与操纵策略，但是都是在结冰完全已知的情况下得出的结论，具有一定的局限性。

为了分析复杂结冰环境对飞机飞行安全包线的影响，首先利用时间尺度分离的方法将飞机运动方程解耦成两个系统，为方便研究选取快子系统为研究对象，以快子系统输出为虚拟输入，建立考虑飞机横向运动(β、φ)的纵向运动方程。然后根据结冰对飞机气动特性的影响，建立考虑结冰位置、冰型及分布等不确定性的复杂结冰环境下的鲁棒气动导数模型。运用可达集理论，得到飞机在不同结冰程度下的飞行安全包线，对结冰条件下飞机滚转运动进行分析。最后进一步分析考虑不同结冰程度下结冰位置、冰型及分布等不确定性结冰情况时的鲁棒飞行安全包线，由此得出结冰不确定性对飞机飞行安全带来的影响。

1 结冰飞机动力学建模

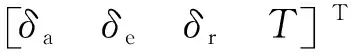
为简化分析过程，以RCAM(Research Civil Aircraft Model)简化模型为研究对象，飞机所有气动参数基于文献[18]。

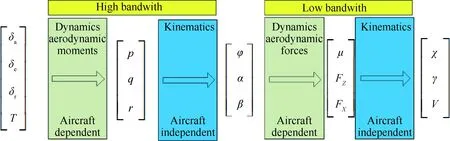
图1 飞机动力学时间尺度分离Fig.1 Time scale separation of aircraft dynamics

1.1 飞机非线性动力学模型

将运动飞机视为一个质点，其受力如图2所示。图中：Xb、Yb分别表示机体坐标系下的纵轴及竖轴；Xω、Yω分别表示速度坐标系下的阻力轴及升力轴；α为迎角；θ为俯仰角。

建立飞机非线性动力学方程:

(1)

式中：m为飞机质量；V为飞行速度；γ为航迹倾角；φ为滚转角；χ为航迹方位角；FX、FY、FZ分别表示沿X、Y、Z轴方向的合力，可表示为

(2)

式中：升力L、阻力D和侧力Y可表示为

(3)

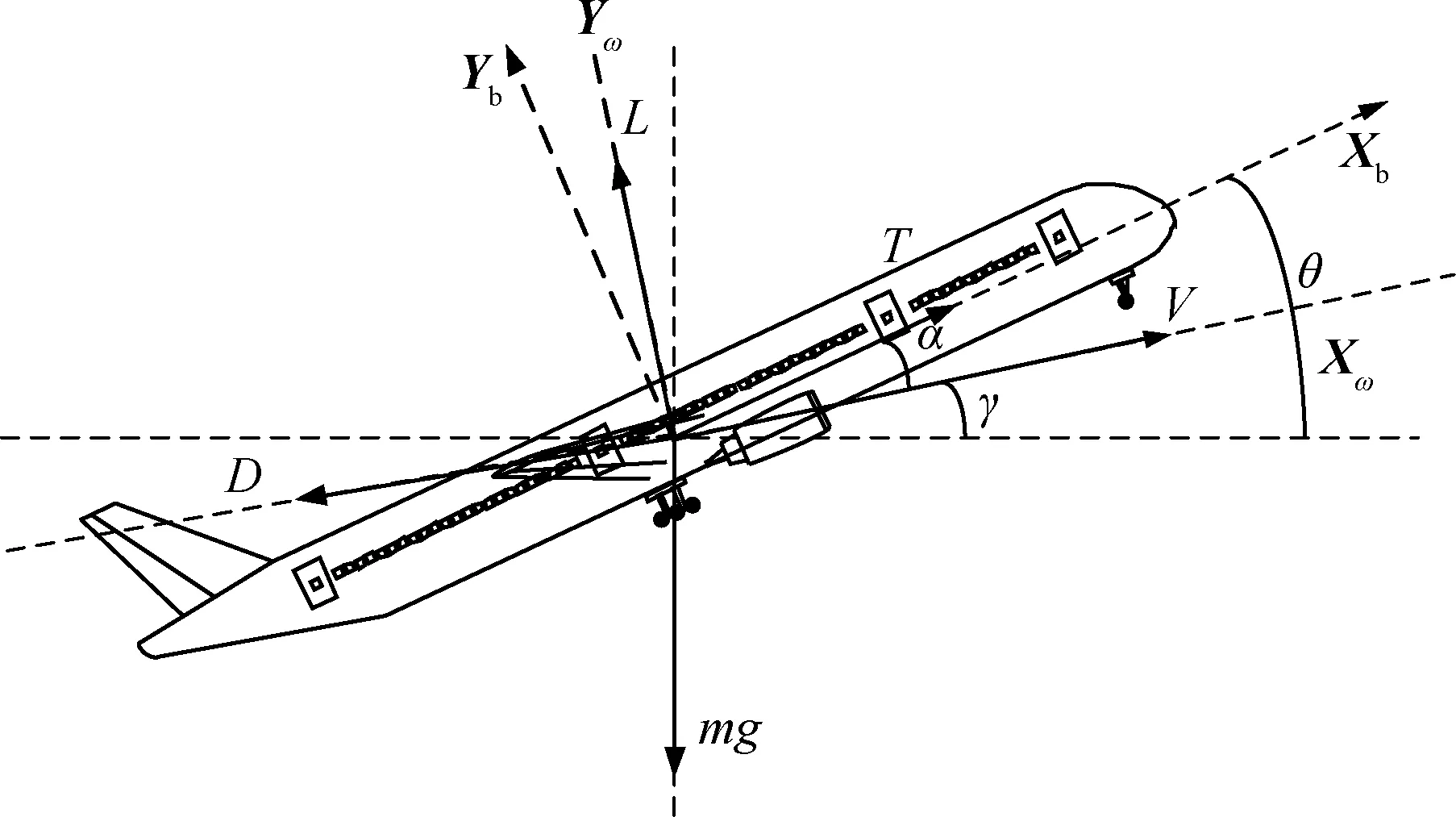
图2 飞机受力质点图Fig.2 Point mass force diagram for aircraft

其中：ρ为空气密度；S为机翼参考面积；CL、CD、CY分别为升力、阻力和侧力系数。

(4)

1.2 飞机结冰模型

飞机结冰是指飞机机体表面的某些部位聚集冰层的现象，主要会导致飞机空气动力学特性变差，升力系数减小、阻力系数增大，同时使得飞机最大飞行迎角减小，如图3所示。

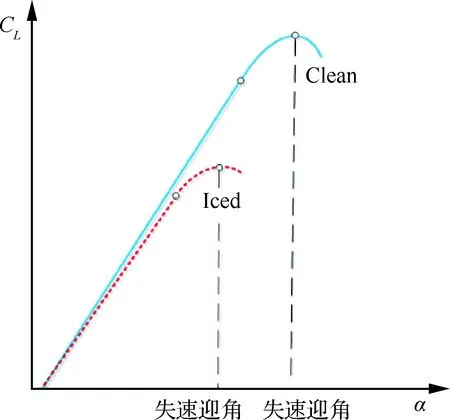
图3 飞机结冰前后升力系数变化示意图Fig.3 Diagram of lift coefficient of aircraft changes in clean and iced

根据Bragg和Basar提出的量化结冰模型，构建结冰程度对飞机气动参数影响的模型[6]：

C(A)iced=(1+ηkC(A))C(A)

(5)

式中：C(A)和C(A)iced分别为飞机结冰前后的某个气动导数值；kC(A)为飞机结冰因子，反映气动导数受结冰影响程度，通常由飞机本身结构决定,对于特定飞机为一个常值；η为表征飞机结冰程度的参数，未结冰时η=0，随着结冰程度的增加，η的值不断增大。

Bragg的结冰模型虽然能够定量反映飞机结冰的影响，但是一方面，飞机结冰程度难以准确测量，另外，结冰是一个非常复杂的过程，不同结冰程度、不同冰型、不同结冰位置等，都会对飞机的气动特性造成不同影响，并不能简单用η来描述。本文针对结冰难以准确量化问题，根据结冰对飞机气动特性的影响，提出鲁棒气动导数模型,可表示为

(6)

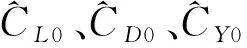
2 可达集及飞行安全包线保护

基于可达集理论，利用可达性分析获得的反向可达集作为结冰飞机最大飞行安全包线，一旦飞行状态超出反向可达集范围，飞机就有失控的危险。

2.1 可达集理论

飞机的动态特性可以表示为一个连续时间控制：

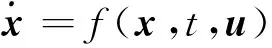
(7)

式中：x∈Rn表示n维状态空间；u∈U⊆Rm表示m维控制量且f(·,·):Rn×U→Rn为有界、连续的Lipschitz函数。

定义状态轨迹为

ξ(x0,t0,u(·),t):t→x∈Rn

(8)

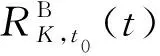
∃tf∈[t,T]|ξ(x,t0,u(·)，tf)∈K}

(9)

式中：K∈Rn为目标集；tf为达到目标集所需的时间。

本文研究飞机在结冰条件下的飞行安全包线，从理论上确定飞机能够安全飞行的最大可操纵范围，而通过可达性分析得到的反向可达集刚好能够求得飞机可以恢复到安全飞行状态的最大范围，因此，选取反向可达集作为复杂结冰条件下的飞行安全包线。

2.2 可达集计算

可达集的求解基本上可以分为两类，包括拉格朗日法和欧拉法[19]。拉格朗日方法利用紧集表示向量场的流向，因此，计算复杂度较高，一般用于计算较高维的可达集；欧拉法主要是以水平集方法为代表，水平集方法用HJB-PDE(Hamilton Jacobi Bellman-Partial Differential Equation)零水平集方程的黏性解表示可达集[20]，该方法将可达性分析与最优控制理论紧密结合起来，能处理复杂的非线性和最优控制策略问题[21]，在航空界应用较为广泛。

2.2.1 水平集方法

利用水平集方程求解时间依赖的Hamilton-Jacobi方程零水平集的黏性解，并将Hamilton-Jacobi方程的黏性解作为可达集的隐式表达式。

水平集方程可以表示为

(10)

式中：φ(x,t)为水平集函数。

目标集K可由水平集函数表示为

K={x∈Rn|φ(x,0)≤0}

(11)

通过计算HJB-PDE方程的黏性解，得到目标集K对应的可达集为

(12)

式中：

(13)

最优控制输入为

u*(x,p)=arg maxpTf(x,t,u)

(14)

表示在状态x下能使哈密尔顿方程H(x,p)达到最大的控制输入。

2.2.2 最优控制输入计算

最优控制输入u*(x,p)在飞控系统中的作用是使飞行状态x的轨迹始终保持在反向可达集内部，最终在t=τ时刻达到目标集。

由式(13)可得本文动力学模型的Hamilton函数为

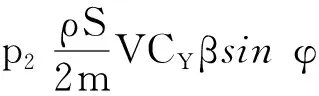
(15)

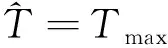
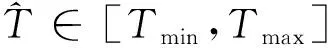
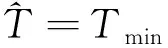
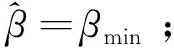
2.2.3 考虑不确定性的可达集

∃tf∈[t,T]|ξ(x,t0,u(·),tf,Δ)∈K}

(16)

HJB-PDE方程可以表示为

(17)

3 结冰飞机的飞行安全包线

以RCAM简化模型为研究对象，对结冰飞机低空平飞阶段的飞行安全包线变化及运动特性进行分析。正常飞行时飞机及飞行相关参数为：飞机质量m=120 000 kg,重力加速度g=9.81 m/s2,飞行高度H=2 000 m,大气密度ρ=1.006 5 kg/m3，最大推力Tmax=410 920 N，最小推力Tmin=20 546 N，机翼参考面积S=260 m2,升力系数CL0=1.065 6、CLα=6.072 5，阻力系数CD0=0.159 9、CDα=0.503 5、CDα2=2.117 5，侧力系数CY=-1.6。

3.1 结冰对飞行安全包线的影响

首先对确定性结冰进行分析，假设飞机机翼发生结冰，参照文献[22]中结冰程度的区分标准，分别定义3种结冰程度η，即η=0，0.1，0.3，分别对应未结冰、轻度结冰、严重结冰。

计算飞机正常情况飞行时在给定目标集下的反向可达集，并以反向可达集作为此条件下飞机的飞行安全包线，如图4所示，在可达集范围内，所有飞行状态都可在最优控制操纵下达到目标集。一旦状态超出可达集边界，飞机将无法恢复到正常飞行状态。

图4 正常条件下飞行安全包线Fig.4 Flight safe envelope in clean condition

计算飞机未结冰(η=0)发生轻度结冰(η=0.1)、严重结冰(η=0.3)时的飞行安全包线，并进行对比，如图5所示。图中绿色、粉色和红色包线分别代表未结冰、轻度结冰及严重结冰时飞机飞行安全包线，由仿真图可以看出，随着结冰程度的增加，飞机的可操纵性下降，飞行安全包线不断收缩，在速度轴V方向上收缩最为严重。当飞机发生严重结冰时，飞机的气动参数发生改变，最大失速迎角减小，最小失速速度增大，飞行安全包线向右收缩，飞机发生失速的危险增大。

考虑在结冰情形下飞机滚转对于飞行安全包线的影响，分别选滚转角φ=0°,30°,60°的情形进行研究，如图6所示。图中绿色、粉色和红色包线分别代表滚转角为φ=0°，30°，60°时的飞行安全包线，通过对不同滚转角下飞行安全包线的比较可以看出，随着滚转角φ的不断增大，飞行安全包线持续减小，且主要表现在γ轴方向上，飞机的爬升性能降低，这主要因为飞机爬升的力由Lcosφ提供，当滚转角增大时，爬升力减小，爬升性能降低。因此当飞机发生结冰时，应当减少滚转机动，以增大飞机爬升与俯冲的安全操纵范围。

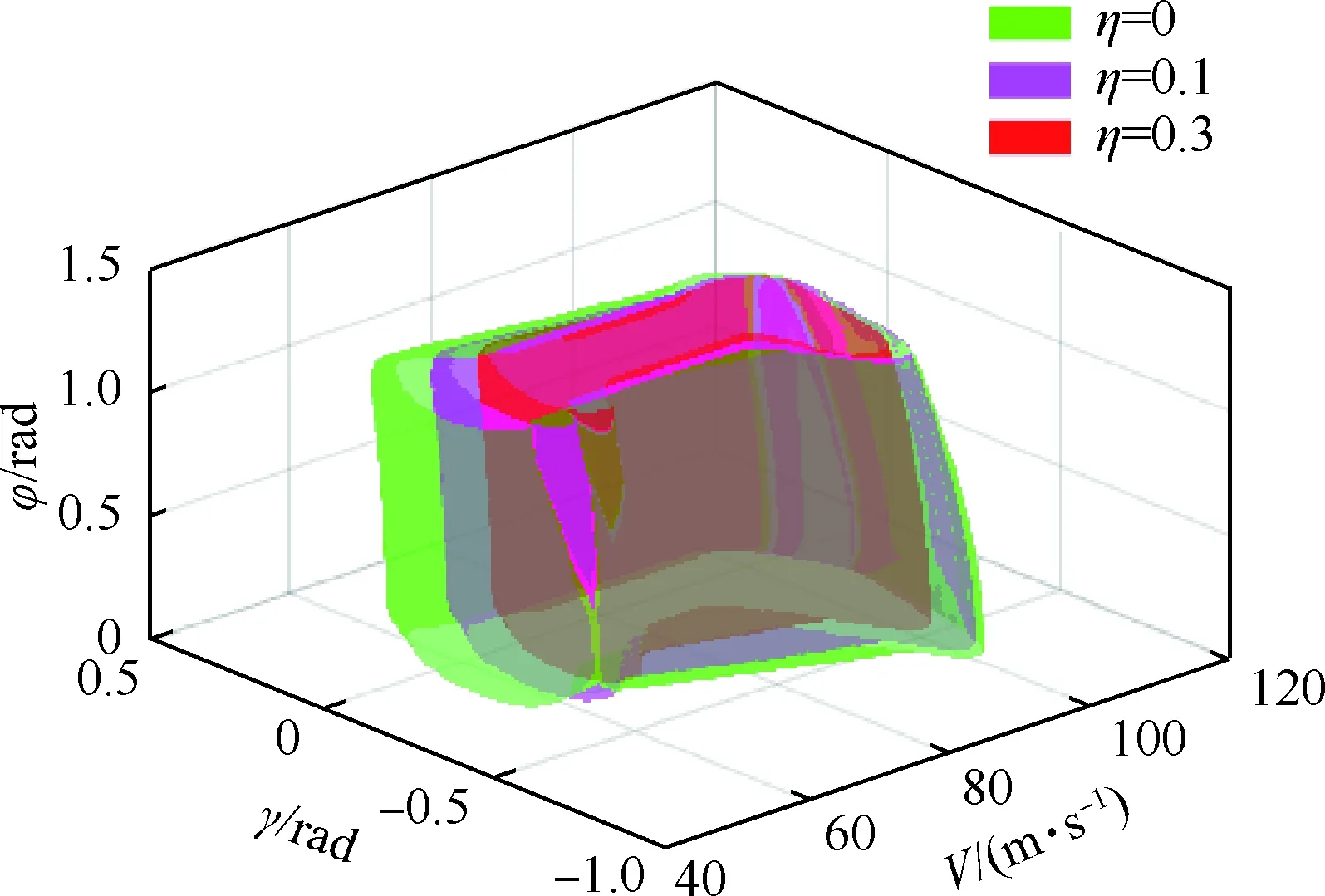
图5 不同结冰程度下的飞行安全包线Fig.5 Flight safe envelope under different icing degrees

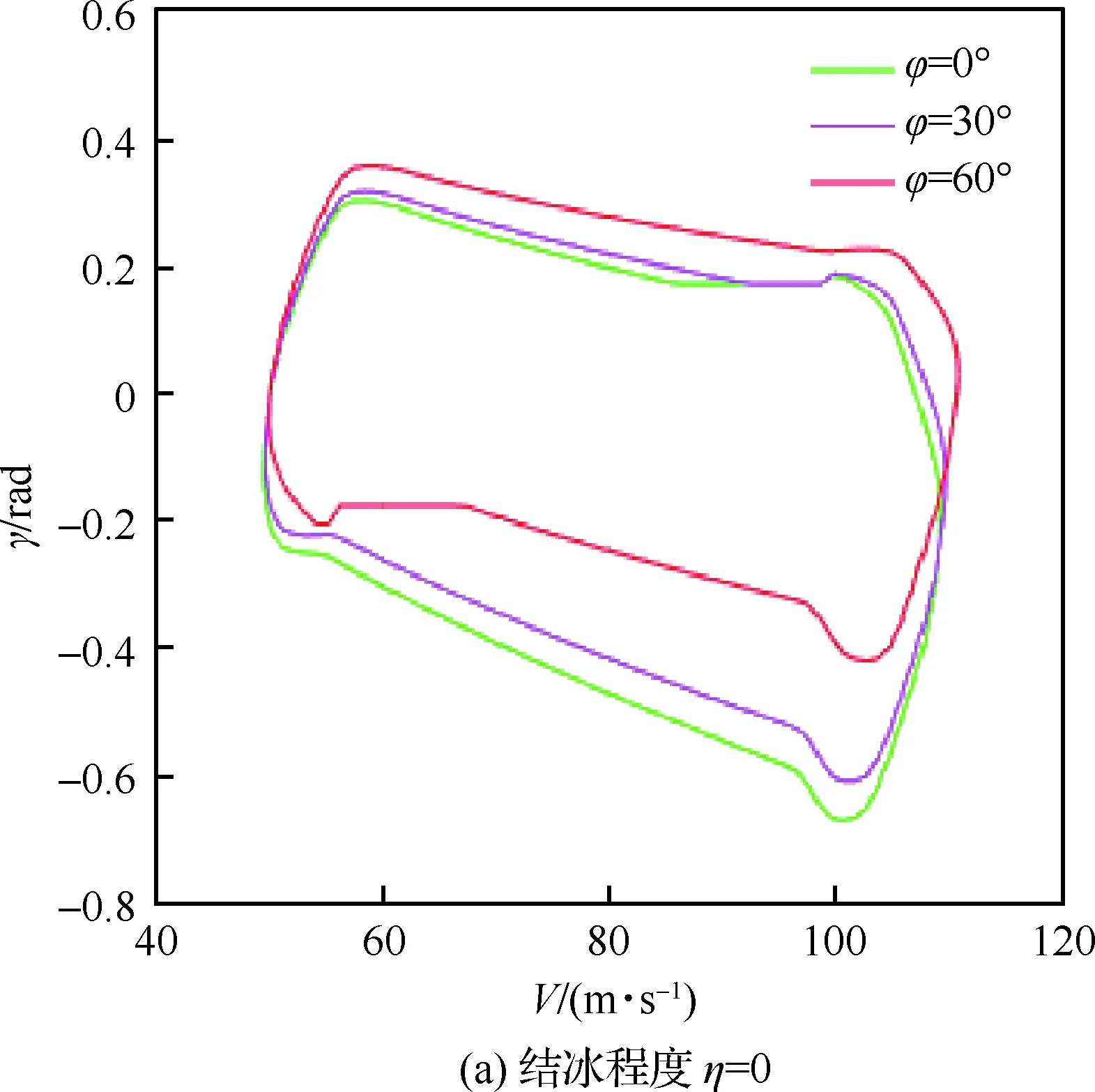
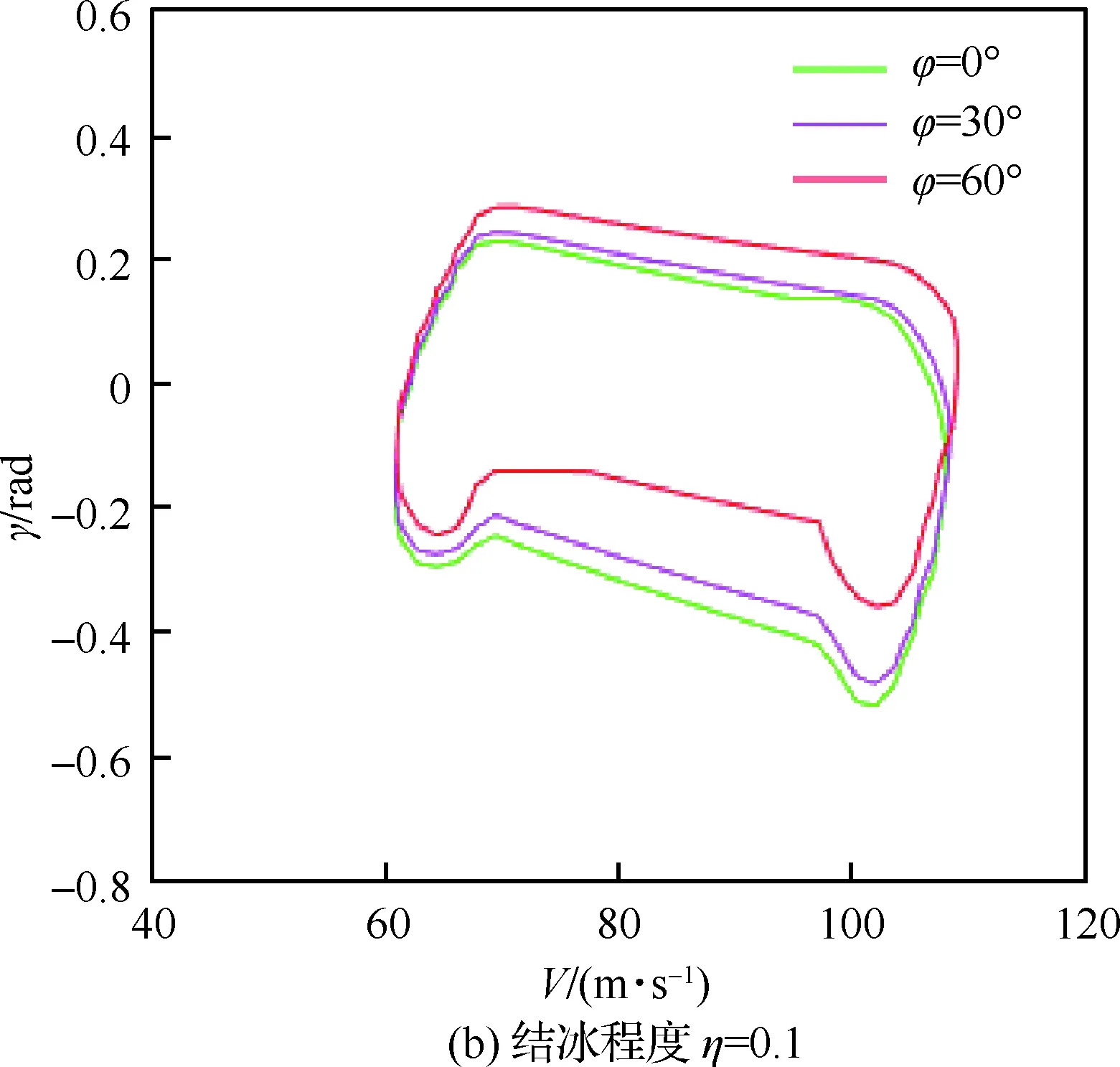
图6 不同滚转角下的飞行安全包线Fig.6 Flight safe envelope at different roll angles

3.2 不确定结冰条件下的飞行安全包线

在3.1节中讨论了在确定性结冰条件下飞机飞行安全包线的变化，但在实际飞行中无法完全获取飞机结冰信息，因此，也无法获得飞机准确的飞行安全包线。在此对结冰程度已知，但结冰位置、冰型及分布等存在不确定性情况下的飞机飞行安全包线进行鲁棒性分析。

根据第1节所建模型，选取高斯分布标准差为3σ(3σ置信度为99%)，不确定量Δ分别为0、20%和30%，对轻度结冰(η=0.1)、严重结冰(η=0.3)时的飞行安全包线进行分析，如图7、图8所示。

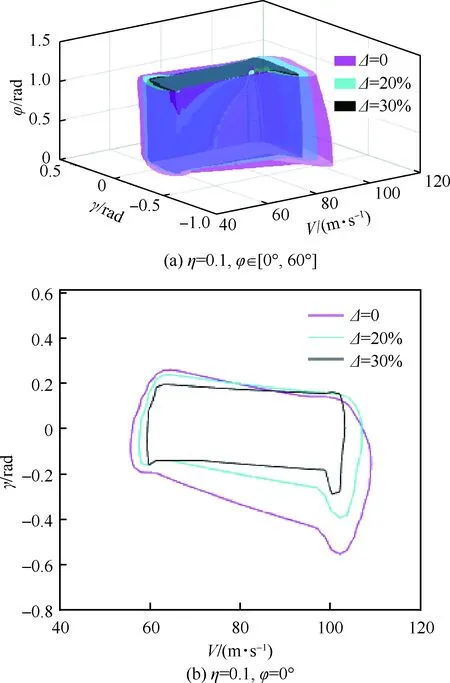
图7 轻度结冰条件下飞行安全包线的变化Fig.7 Changes of flight safe envelope under mild icing condition

图8 严重结冰条件下飞行安全包线的变化Fig.8 Changes of flight safe envelope under severe icing condition

图7中蓝色曲面和黑色曲面分别表示飞机在轻度结冰(η=0.1)条件下，不确定量Δ分别为20%和30%时的飞行安全包线。由于结冰位置、冰型及分布等存在不确定性，使得气动导数变化不确定，当考虑Δ=20%时，鲁棒飞行安全包线相较确定性安全包线在φ=0°收缩了30%，当考虑Δ=30%时，鲁棒飞行安全包线相较确定性安全包线在φ=0°收缩了45%。

图8中蓝色曲面和黑色曲面分别表示飞机在重度结冰(η=0.3)条件下，不确定量Δ分别为20%和30%时的飞行安全包线。当考虑Δ=20%时，鲁棒飞行安全包线相较确定性安全包线在φ=0°收缩了15%，当考虑Δ=30%时，鲁棒飞行安全包线相较确定性安全包线在φ=0°收缩了35%。

通过对比可知，结冰位置、冰型及分布等不确定性因素对轻度结冰时的飞行安全包线的影响大于重度结冰时的影响，这主要是由于确定性轻度结冰时飞机的气动导数变化相对较小，飞机所处于的状态仍然为平衡状态，但是当考虑不确定性时，气动导数变化增大，原平衡点的性质发生了改变，由稳定的平衡点变为不稳定平衡点。因此，当考虑不确定性时，轻度结冰条件下飞行安全包线收缩更加严重。

4 结 论

建立了考虑横向运动(β、φ)的飞机纵向运动模型，基于可达集理论利用可达性分析研究了飞机在确定性结冰条件下和考虑结冰位置、冰型及分布等不确定性结冰条件下飞机的飞行安全包线，分析了不同结冰程度(η=0,0.1,0.3)对于飞行安全的影响，得出以下结论：

1) 以反向可达集作为飞行安全包线相较于传统包线具有明显优势，并且在外部环境发生变化时，仍然能够指导飞行员操纵。

2) 随着结冰程度的增加，飞行安全包线的范围不断收缩，主要体现在速度轴方向上，飞机的气动参数发生改变，最大失速迎角减小，最小失速速度增大,包线向右收缩。

3) 当考虑滚转角φ对结冰飞机飞行安全包线影响时，随着φ的增大，飞行安全包线主要沿着γ轴方向收缩，飞行安全包线减小。因此，当飞机发生结冰时，应尽量减小滚转角φ同时避免俯冲机动，以提高飞行安全。

4) 当考虑结冰位置、冰型及分布等不确定性结冰情况下的鲁棒飞行安全包线时，不确定量Δ对于飞行安全包线影响较大，且不确定性因素对轻度结冰时的飞行安全包线的影响大于重度结冰时的影响。因此，即使飞机只是发生轻度结冰但是由于结冰位置、冰型及分布等的不确定性，飞行风险仍然较大，飞行员应该保持警惕，适当缩小操纵范围。