基于自适应Kriging代理模型的交叉熵重要抽样法
史朝印,吕震宙,李璐祎,王燕萍
西北工业大学 航空学院,西安 710072
结构可靠性分析的主要任务在于计算结构失效概率[1],迄今为止,研究者们已经提出了许多高效的可靠性计算方法。基于设计点的方法[2-4]是最为常见的一种可靠性分析方法,其中,一次二阶矩方法[4]最具有代表性,它通过将极限状态函数在设计点处进行泰勒展开,保留展开式一阶项,从而实现对极限状态函数的线性近似。但该方法需要计算极限状态函数在设计点处的梯度,且此方法的准确度严重依赖于所研究问题的线性特征。对于具有复杂失效域的问题,其失效域往往是数量众多的不连通域,且每个失效域相对于整个取值域占比较小,失效域的个数难以预先得到,设计点也难以预先求解。因此该方法无法解决复杂失效域、多设计点等问题。数字模拟方法中最基本的蒙特卡罗模拟(Monte Carlo Simulation, MCS)方法通过抽样并判断样本所处状态,计算结构失效概率。对于实际工程问题,失效概率通常较小(10-3量级及更小),导致MCS方法往往需要大量的样本(一般为102~104/Pf,Pf为结构真实失效概率),才能获得收敛解,计算效率低下。因此,研究者们提出了一系列改进数字模拟方法。其中,重要抽样(Importance Sampling, IS)法[5-8]是一种应用广泛的方差缩减方法,它通过构建重要抽样密度函数,使所抽取的样本尽可能多地落入失效域中,从而大幅缩小抽样样本池规模,提高失效概率的计算效率。
重要抽样方法的关键在于重要抽样密度函数的构建。Melcher[9]提出了基于设计点的方法,通过将原随机变量概率密度函数的中心平移至设计点处构建重要抽样密度函数。但该方法无法处理多设计点、复杂失效域的问题。吴斌等[10]提出了扩大方差的方法,这种方法难以确定方差扩大的倍数。Priebe和Marchette[11]提出了混合重要抽样法,对每个失效模式单独构造重要抽样密度函数后加权混合,有效解决了多失效模式问题。Au和Beek[12]提出了基于核密度估计的方法,通过马尔可夫链对失效域进行预抽样,获得一定量的失效样本后,通过核密度估计得到重要抽样密度函数;但核密度估计方法计算成本较大,且精度难以保证。Dubourg等[13]提出了元模型重要抽样(Meta-IS)方法,使用Kriging模型近似理论上最优重要抽样密度函数,同时,将失效概率转化为失效概率估计值和修正系数乘积的形式;但该方法在Kriging构建时收敛标准的物理意义并不明确,且需要大量调用极限状态函数以计算样本的真实响应值。Cadini等[14]提出了改进的Meta-IS-AK2方法,但该方法通过单高斯模型获得的重要抽样密度函数针对多失效域问题效率较低。Kurtz和Song[15]提出了交叉熵重要抽样(Cross Entropy Importance Sampling, CE-IS)方法,使用高斯混合模型作为重要抽样函数,通过交叉熵原理,迭代更新高斯混合模型(Gaussian Mixture Model, GMM)的参数,逐步逼近最优重要抽样密度函数。该方法较Meta-IS-AK2获得的重要抽样密度函数有更高的抽样效率,但在GMM的参数计算过程中,需大量调用极限状态函数计算样本点处真实输出响应值,使得最终的计算效率大幅下降。且Kurtz和Song[15]所提方法以落入失效域的重要样本比率作为收敛准则,没有考虑失效概率估计值的变异系数,对于部分问题,会存在解不稳定,迭代次数过多,甚至无收敛解的问题。
对于实际工程问题,极限状态函数往往是基于有限元模型[16]的隐式函数,每次调用都会带来大量的计算量,因此,应尽可能减少极限状态函数的调用次数。代理模型[17-22]可以有效避免极限状态函数多次调用问题,其通过一定的选点准则,筛选出对失效概率计算影响较大的点,添加至模型训练集,构建代理模型预测样本点处的响应值,计算结构失效概率。其中,Kriging模型由于其在可靠性分析领域存在特有的优势受到了最为广泛的关注。Kriging模型假设样本点之间服从高斯随机过程,通过极大似然估计模型参数值。由于高斯过程的特性,Kriging模型不仅可以预测样本点处的响应值,还可以预测样本点处的方差值。因此,Kriging模型有别于其他代理模型,对于样本点的预测具有随机属性,可以提供样本点的统计信息,与可靠性分析通过输入变量统计信息求解输出响应部分统计信息的思想相吻合。基于此,研究者们提出了一系列的学习函数,自适应地筛选出训练样本点,以提高Kriging模型的构建效率。常用的自适应学习函数有期望可行性函数[23]、U学习函数[24]、H学习函数[25]、期望最大学习函数[26]等。其中,U学习函数综合考虑样本点距极限状态面的距离和样本点的预测误差,筛选出最易错误判断失效状态的点,简单易行,本文选择U函数作为学习函数。通过自适应Kriging(Adaptive Kriging, AK)代理模型方法,来用少量训练样本即可构建高精度的收敛的代理模型替代极限状态函数,显著提高失效概率的计算效率。常用的AK-MCS[24]依旧需要构建大规模的样本池,对于小失效概率问题,计算效率依旧低下。
本文将CE-IS方法与AK方法相结合,通过少量训练样本,自适应地拟合极限状态面,减少CE-IS的极限状态函数调用次数,同时通过GMM,构建高效的重要抽样函数,大幅缩小AK-MCS方法的样本池规模。相较于现有方法,本文所提方法有以下创新性:
1) 改进CE-IS方法收敛条件,避免冗余迭代,同时增强CE-IS方法的适用性。
2) 通过AK模型拟合极限状态函数,可显著减少CE-IS方法的计算量。
3) 通过GMM近似最优重要抽样密度函数,相较于现有的重要抽样密度函数的构造方法,更为高效。
1 基于交叉熵的重要抽样法
1.1 重要抽样法
结构可靠性分析的关键是失效概率的计算,对于已知结构,其极限状态函数为g(x),其中,x为随机输入变量,其概率密度函数为fX(x),结构的失效域为F={x|g(x)≤0},失效概率Pf即为输入随机变量落入失效域的概率,可由积分求得,即
(1)
式(1)通常无解析解,故常采用MCS方法作为参照解。引入失效域指示函数IF(x):
(2)
则通过MCS方法估计结构失效概率的表达式为
(3)
式中:xi(i=1,2,…,N)为N个按fX(x)抽取的MCS样本点;Rd为d维的实数域。
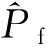
(4)
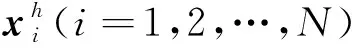
(5)
理论上可以推导最优的重要抽样密度函数hopt(x)为
hopt(x)=IF(x)·fX(x)/Pf
(6)
以hopt(x)作为重要抽样密度函数时,失效概率估计值的方差为零。通过对最优重要抽样密度函数进行近似拟合,即可得到抽样效率最高的重要抽样密度函数。
1.2 高斯混合模型
假设随机向量x服从K元高斯混合分布,其概率密度函数p(x)为
(7)
式中:K为高斯混合成分个数;f(x|μk,Σk)为第k个混合成分的混合高斯分布密度函数,μk和Σk分别为相应均值向量和协方差矩阵;πk为混为混合成分系数,由密度函数的归一化条件知,πk应满足:
(8)
0≤πk≤1
(9)
式中:混合系数πk表示随机变量x来自于第k个混合成分的概率。
记二值随机变量zk(k=1,2,…,K)表示在给定样本x的情况下,其是否由第k个混合变量生成,zk的后验概率为
(10)
对于一个未知K元混合高斯分布模型
(11)
其未知参数v共3×K组,每一元高斯分布的参数为{πk,μk,Σk},则
v={πk,μk,Σk;k=1,2,…,K}
(12)
通过交叉熵准则,可以迭代求出K元混合高斯分布的参数,使其尽可能地逼近理论最优重要抽样密度函数。
1.3 交叉熵准则
在信息论中,Kullback-Leibler交叉熵(K-L Cross-Entropy,KL-CE)D,简称交叉熵(Cross-Entropy,CE)常用来度量函数的差异,其定义为
(13)
由式(13)可知,交叉熵越小,函数f(x)与函数g(x)之间的差异就越小。为了使p(x;v)逼近最优重要抽样密度函数hopt(x),计算它们之间的交叉熵:
lnp(x;v)dx
(14)
将式(6)代入式(14)可得
(15)
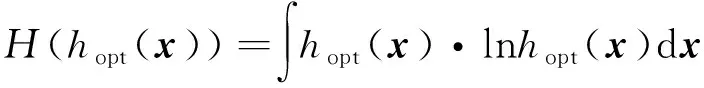
arg maxEX[IF(x)·ln(p(x;v))]
(16)
式(16)为嵌套形式,通常无解析解,一般采用迭代算法求解,逐步更新GMM参数,直至满足收敛要求。
为了提高计算效率,每一步迭代也采用重要抽样法进行计算,即,使用前一步迭代所得GMMp(x;w)作为当前重要抽样密度函数,w为其参数。式(16)可改写为
p(x;w)dx=arg maxEX~p(x;w)[IF(x)·
ln(p(x;v))·W(x)]
(17)
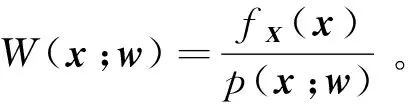
(18)
(19)
将GMM的定义式(7)代入式(19),得到关于模型参数v的方程:
(20)
分别对3×K组模型参数求导,以均值向量μk(k=1,2,…,K)为例,可建立方程为
(21)
解得
(22)
同理可得Σk和πk(k=1,2,…,K)的表达式为
(23)
(24)
式(22)~式(24)即为基于交叉熵原理得到的GMM参数更新准则,通过多次迭代,GMM即可较为准确地近似最优重要抽样密度函数hopt(x)。但注意到,式(22)~式(24)中失效域指示函数IF(x)的计算需要调用结构极限状态函数,而多次迭代会使得计算量显著加大,因此,本文将AK方法与CE-IS方法相结合,从而提高算法的效率。
2 CE-IS-AK算法
2.1 Kriging模型

Y=f(x)Tβ+z(x)
(25)
式中:f(x)=[f1(x)f2(x) …fM(x)]T为M×1维基函数向量;β=[β1β2…βM]T为相应的系数向量;z(x)为零均值高斯随机过程,协方差函数为
(26)

(27)
(28)

R=
(29)
由上述过程可知,Kriging模型的构建即为相关函数参数θ的确定,采取最大似然估计计算最优参数为
(30)
(31)
[FR-1r(x)-f(x)]T(FTR-1F)-1·
[FR-1r(x)-f(x)]}
(32)
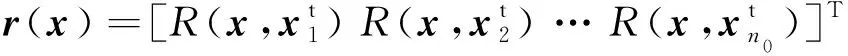
2.2 自适应Kriging模型
为了高效地选择模型训练点,通常需采取自适应的方法,选择恰当学习函数与收敛条件。本文选择的U学习函数表达式为
(33)
U函数表征了样本输出响应y=g(x)的正负状态被误分的概率。U函数值越小,样本点被错误分类的概率越大,故而筛选出U函数值较小的样本点作为新的训练点:
(34)
式中:S为候选样本池。
U(x)=2时,样本点被正确分类的概率为1-Φ(2)=97.7%,故可以认为当U(x)≥2时,所构建的Kriging模型对样本点的正负号判断有超过97.7%的概率预测正确。因此,确定Kriging模型构建的收敛条件为
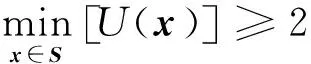
(35)
2.3 本文所提算法
本文所提方法结合了CE-IS方法与AK方法,避免了CE-IS方法计算量过大的缺陷,并提出了新的收敛准则,避免了冗余迭代,增强了CE-IS算法的适用性。同时,较AK-MCS方法缩减了样本池,使小失效概率的计算更为高效。以下给出本文所提方法的详细计算步骤。

4) 用Kriging模型计算样本池S(l)中样本点U函数值。
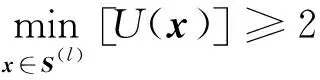
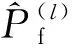
(36)

7) 计算抽样效率:
(37)
判断η是否大于指定值η*,如满足,则执行第8)步;否则,根据式(22)~式(24)更新GMM参数,增加迭代次数l=l+1,转跳至第3)步。
8) 扩大样本池规模,如:N=10N,转跳至第3)步。
方法流程图如图1所示。
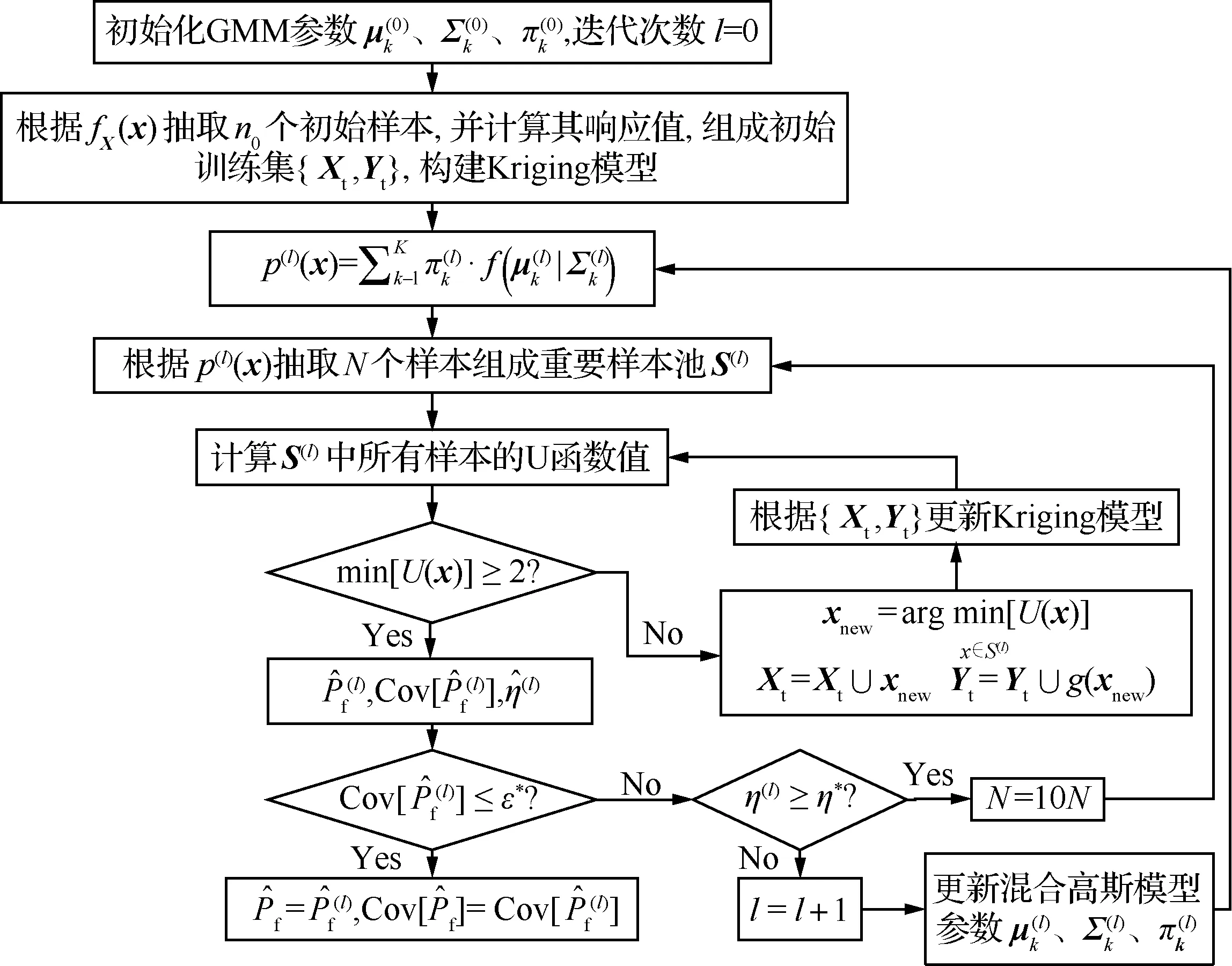
图1 CE-IS-AK方法流程图Fig.1 Flow chart of CE-IS-AK method
2.4 一些讨论及说明
文献[15]以其所提ρ分位数作为收敛准则,ρ分位数的概念与抽样效率η概念相同,均表征重要样本落入失效域中的比例;以其作为收敛准则,即以抽样效率η作为收敛准则,存在以下3个主要问题:
1) 对于部分复杂失效域问题,由于理论最优重要抽样密度函数的高度非线性以及不连续性,GMM难以十分准确地逼近理论最优重要抽样密度函数,单纯以抽样效率作为收敛准会造成方法迭代次数过多,甚至不收敛。
2) 对于部分失效概率较大的问题,只需较少的样本点即可得到稳定的解,以抽样效率作为收敛指标会使算法进行多次无意义迭代。
3) 对于部分极小失效概率问题,即使使用重要抽样的方法,也需要较大规模的样本池,仅通过抽样效率难以判断是否得到了稳定的收敛解。
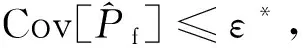
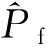
本文以失效概率估计值的变异系数作为方法收敛准则,可以准确衡量解的稳定性,以及样本池规模是否恰当,同时避免方法出现冗余迭代。
本文构建AK模型用于拟合极限状态函数,因此,每次更新重要样本池时,无需重新构建模型,仅需在原有Kriging模型的基础上,通过学习函数添加少量训练样本点,修正现有模型,即可完成收敛。
根据文献[15]的研究,本文建议高斯混合模型中混合成分数目K的取值应满足如下要求:
max{d,Ncomponent}≤K≤5%ηNNcomponent
(38)
式中:Ncomponent为结构失效模式数目,对于单模式问题Ncomponent=1。建议迭代样本池规模N为103~105。
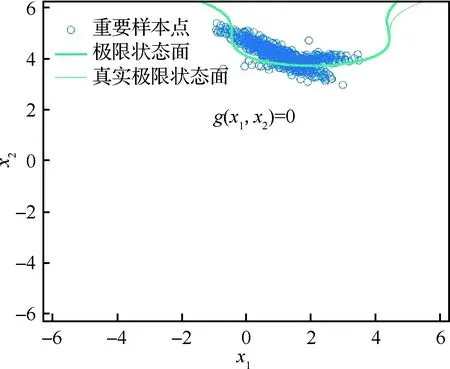
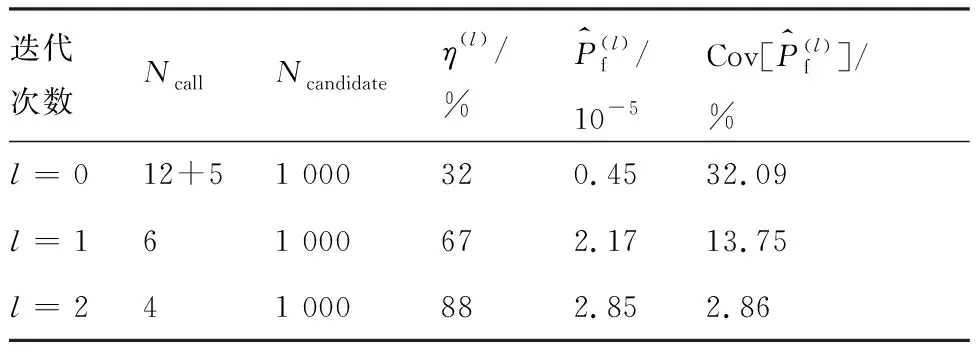
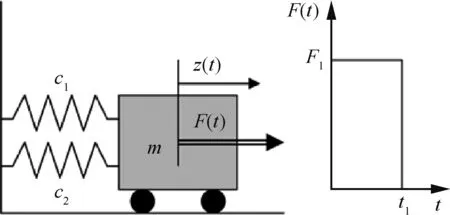
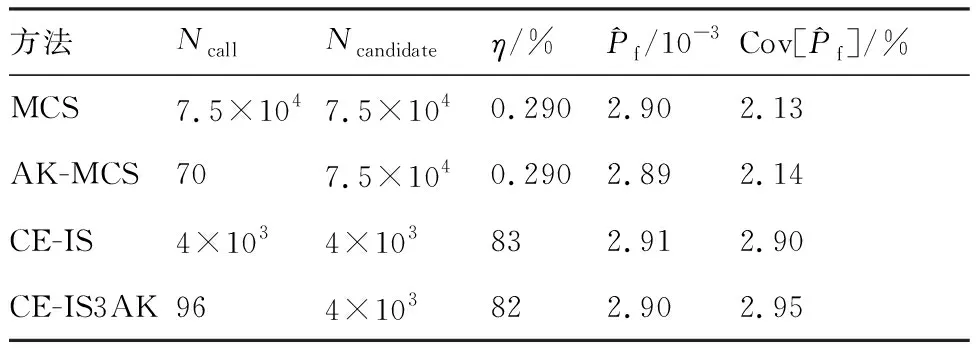
对于复杂失效问题,往往难以预先判断其失效域个数,因此建议选择d 本节给出5个算例证明所提算法的高效与适用性,第1个算例为小失效概率问题;第2个算例为串联系统问题,具有多失效域;第3个算例为复杂多失效域问题,不连续失效域较多,失效边界复杂;第4个算例为一个动态非线性振子问题;第5个算例为工程有限元算例。本文将所提方法与AK-MCS和CE-IS等方法所得结果进行对比。 一个非线性单设计点问题的极限状态函数为 g(x1,x2)=0.5(x1-2)2-1.5(x2-5)3-3 (39) 输入随机变量为标准正态变量,图2给出了算例一通过CE-IS-AK方法最终所得的重要样本点和极限状态面以及真实极限状态面。表1给出了算例一CE-IS-AK方法具体迭代结果,表2给出了算例一的各方法计算对比结果,表中,Ncall为极限状态函数调用次数,Ncondidate为备选样本点总数。 针对此算例,本文选择混合成分的个数K=20,每次迭代的样本池规模为N=103,收敛条件为ε*=5%,η*=80%。从算例1结果可看出,本文所提方法具有较高的效率,这是由于GMM模型本身的特性,可以对不连续的多失效域进行近似。通过3次迭代,方法即收敛。相较于CE-IS方法,本文所提方法在大幅减小极限状态函数调用次数的情况下,依旧保持了与其相当的高抽样效率;与AK-MCS方法相比,本文在极限状态函数调用次数基本相当的情况下,大幅度缩减了样本池规模,在实际计算中,大幅提升了计算效率。 图2 算例1 CE-IS-AK方法所得重要样本点及 极限状态响应面Fig.2 Approximate LSF and important samples obtained by CE-IS-AK of Example 1 表1 算例1 CE-IS-AK方法迭代结果 Table 1Results of iteration of CE-IS-AK of Example 1 迭代次数NcallNcandidateη(l)/%P^(l)f/10-5Cov[P^(l)f]/%l=012+51 000320.4532.09l=161 000672.1713.75l=241 000882.852.86 表2 算例1的计算结果Table 2 Results of Example 1 串联系统具有4个失效域,其极限状态函数为 g(x1,x2)= (40) 式中:输入随机变量均为标准正态变量。 图3给出了算例2通过CE-IS-AK方法最终所得的重要样本点、极限状态面以及真实极限状态面。表3给出了算例2 CE-IS-AK方法具体迭代结果,表4给出了各方法计算对比结果。 针对此算例,本文选择混合成分的个数K=50,每次迭代的样本池规模为N=103,ε*=5%,迭代门限值为η*=80%。 CE-IS方法只考虑抽样效率,故出现了冗余迭代的情况。而由于本文提出了更加合理的收敛条件,在失效概率估计值的变异系数满足要求后即收敛,虽然最终得到的抽样效率略低于CE-IS方法,但求解精度并无显著区别,且计算量有所减小,若再进行一次迭代即可得到与CE-IS方法相近的求解情况。与AK-MCS方法相比,本文所提方法虽然调用极限状态函数次数有所增加,但样本池规模远远小于AK-MCS方法,避免了对非常大一部分安全域内的样本点进行无意义的Kriging模型的反复多次预测。 图3 算例2 CE-IS-AK方法所得重要样本点及 极限状态响应面Fig.3 Approximate LSF and important samples obtained by CE-IS-AK of Example 2 表3 算例2 CE-IS-AK方法迭代结果 Table 3 Results of iteration of CE-IS-AK of Example 2 迭代次数NcallNcandidateη(l)/%^Pf/10-3Cov[^P(l)f]/%l=030+351 000541.7132.09l=1421 000672.226.75l=2371 000762.223.66l=3181 000882.222.94 表4 算例2的计算结果Table 4 Results of Example 2 注:(3)*表示迭代到l=2,(4)*表示迭代到l=3。 一经典的复杂高度非线性多失效域问题的极限状态函数为 (41) 式中:输入随机变量均为标准正态变量。表5给出了算例3的各种方法的计算结果。图4给出通过所提方法最终所得的重要样本点、近似极限状态面以及真实极限状态面。 针对算例3,本文选择混合成分的个数K=100,每次迭代的样本池规模为N=103,ε*=5%,η*=80%。此算例为一高度非线性多失效域算例,失效域数量较多,面积均较小且较为分散,理论上难以获得抽样效率较高的重要抽样密度函数,但此算例失效概率较大,因此并不需要特别大量的重要样本点即可得到收敛解。CE-IS方法由于仅以抽样效率作为收敛指标,故没有得到收敛的解。本文所提方法虽然最终抽样效率较之前算例有明显下降,但依旧得到了较为准确的收敛解,同时,抽样效率仍为所有对比方法中最高且样本池规模最小。故而,相对于其他对比方法而言,仍然具有较大优势。 表5 算例3的计算结果Table 5 Results of Example 3 图4 算例3 CE-IS-AK方法所得重要样本点及 极限状态响应面Fig.4 Approximate LSF and important samples obtained by CE-IS-AK of Example 3 一单自由度无阻尼弹簧振子模型,系统结构示意图见图5,系统的极限状态函数为 (42) 针对此算例,选择混合成分的个数K=100,每次迭代的样本池规模为N=103,ε*=5%,η*=80%。此算例的各方法对比结果证明了本文所提算法对较高维数的问题依然可以高效处理。 图5 单自由度无阻尼弹簧振子模型Fig.5 Model of single degree of freedom undamped spring oscillator 表6 算例4输入随机变量分布参数 Table 6Distribution parameters of input random variables of Example 4 随机变量分布类型均值标准差m正态分布10.05c1正态分布10.1c2正态分布0.10.01r正态分布0.50.05F1正态分布10.2t1正态分布10.2 表7 算例4的计算结果Table 7 Results of Example 4 以桁架中点位移u(X)为研究对象,结构极限状态函数为: g(X)=τ-u(X) (43) 式中:τ=12 cm为位移u(X)的阈值。 相应地,结构失效域为F={X|g(X)≤0}。算例5无法通过结构力学知识解析得到u(X)的具体表达式,因此,采用有限元仿真对其进行计算。 图6 桁架结构示意图Fig.6 A sketch of truss 表8 算例5输入随机变量分布参数 Table 8Distribution parameters of input random variables of Example 5 随机变量分布类型均值标准差E1,E2/Pa对数正态2.1×10112.1×1010A1/m2对数正态2×10-32×10-4A2/m2对数正态1×10-31×10-4P1,P2,…,P6/N耿贝尔5×1047.5×103 本文采用规模为1×106的MCS样本池,虽然在计算过程中需大量调用有限元模型,但由于该结构较为简单,有限元模型计算迅速,因此,仍可通过MCS方法得到参照解。表9中给出了该工程算例的计算结果。同时,各方法均由同一计算机进行计算验证,其计算时间T一并列出。 表9 算例5的计算结果Table 9 Results of Example 5 针对此算例,选择混合成分的个数K=100,每次迭代的样本池规模为N=103,ε*=5%,η*=80%。 本文所提算法可高效处理复杂失效域与小失效概率耦合问题,即结构系统的失效域较复杂且同时失效概率也较小的问题。 对于小失效概率问题,常规的数字模拟方法,需要规模巨大的样本池来保证计算的精度。所提方法使用基于高斯模型的重要抽样法,大幅度缩减了样本池规模。同时,引入自适应Kriging代理模型辅助计算,减少了功能函数的调用次数,进一步提高了计算效率。算例1所示结果也证明了本文所提方法能在精度范围要求内高效处理小失效概率问题。 对于复杂失效域问题,往往是串并联系统问题、隐式函数问题,甚至是有限元模型问题,针对此类问题,常规代理模型方法虽然能减少计算成本巨大的功能函数的调用次数,但由于样本池规模所限,计算时间成本依旧较大。本文所提方法引入基于高斯混合模型的重要抽样法,极大地缩减了样本池的规模,使计算效率进一步提高。算例2、算例3、算例4和算例5的计算结果也验证了本文所提方法的高效性。 1) 本文针对复杂失效域和小失效概率耦合的失效概率计算问题,提出了交叉熵重要抽样结合自适应Kriging模型的CE-IS-AK方法。通过交叉熵准则指导高斯混合模型逐步逼近理论最优重要抽样密度函数,参数更新中使用AK模型近似计算样本响应值,从而大大减少了计算过程中的结构极限状态函数调用次数,在保证方法计算精度的同时提高了CE-IS方法的计算效率。 2) 本文改进了CE-IS方法的收敛准则,以失效概率估计值的变异系数作为最终指标,抽样效率作为参考指标,避免了冗余迭代,也克服了CE-IS方法对于部分复杂失效域问题无法得到收敛解的缺点,扩大了方法的适用范围。 3) 相较于CE-IS方法,由于AK模型的引入,结构极限状态函数的调用次数大幅缩减,计算效率显著提高。相较于AK-MCS方法,由于采用了高斯混合模型代替重要抽样密度函数,抽样效率较MCS方法得到了显著提高,样本池规模大幅缩小,适用于小失效概率问题。同时,由于利用了高斯混合模型,方法对于多失效域和复杂失效域等问题也有良好的适用性。最后,算例分析结果也证明了本文所提方法的高效性。3 算例分析
3.1 算例1

3.2 算例2
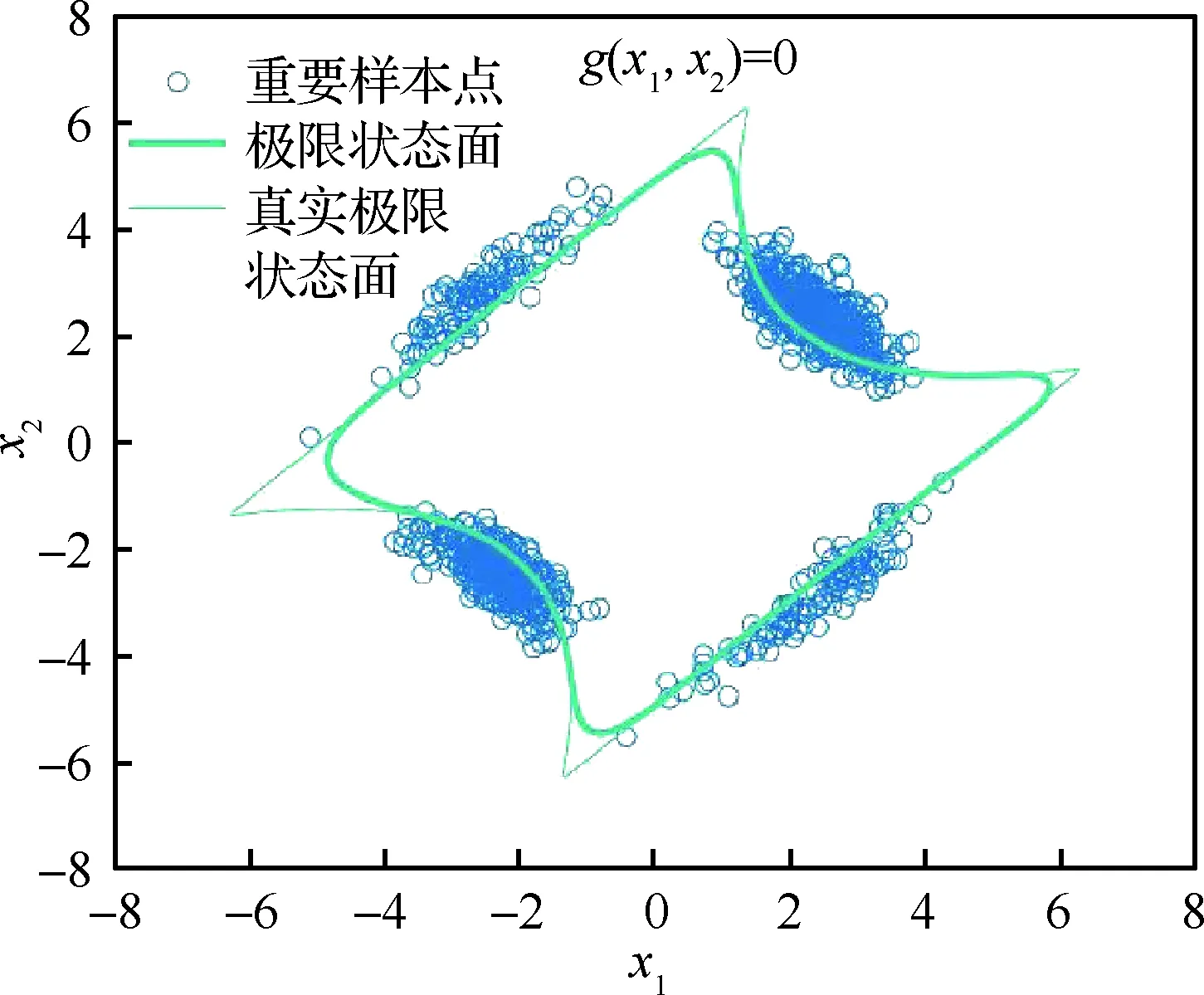

3.3 算例3

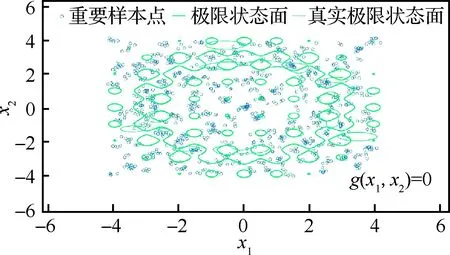
3.4 算例4
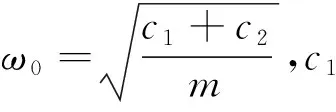

3.5 算例5



3.6 一些讨论及说明

4 结 论

