基于变权重变异鸽群优化的无人机空中加油自抗扰控制器设计
费伦,段海滨,2,*,徐小斌,鲍瑞,孙永斌
1. 北京航空航天大学 自动化科学与电气工程学院, 北京 100083 2. 鹏城实验室, 深圳 518000
空中加油 (Aerial Refueling) 技术是加油机在航行中为受油机补充燃料的技术,可以显著提高战斗机的续航能力[1]。在空中加油任务中,由于尾流等影响,需要受油机具有较高的控制精度,因此需要设计控制精度高、抗干扰能力强的控制系统。Nicol等[2]在2011年提出了一种直接近似的自适应控制方法,依靠一组先验的权重来指导学习,从而更新控制器的权重。Enomoto等[3]在2008年采用内外环动态逆方法,设计了无人机制导跟踪控制系统,该系统能够实现与目标无人机保持理想的相对距离。但动态逆系统控制器使用在空中加油的对接阶段,会造成逆误差,不能满足对接阶段的控制要求。Lungu[4]于2019年设计了一种基于动态反步控制的自动着陆飞行控制系统,验证了该控制结构在不同初始条件下的稳定性和鲁棒性,由于其控制算法需要基于准确的数学模型,其实现有一定的困难。
自抗扰控制(Active Disturbance Rejection Controll, ADRC)技术是Han在20世纪80年代所提出的一种新的控制理论,这种控制不依赖于受控对象的具体数学模型,具有很强的鲁棒性和抗干扰性[5]。自抗扰技术广泛地在控制工程领域应用[6-10]。相比于经典的比例-积分-微分(Proportional-Integral-Derivative, PID)控制器,自抗扰控制器的控制效果更为优越,系统的稳健性更强。但自抗扰控制同样存在控制器参数众多,整定参数往往依靠工程经验等问题,不容易得到最优控制效果[11]。
鸽群优化(Pigeon Inspired Optimization, PIO)是在2014年提出的一种启发式优化仿生算法[12],该算法基于鸽群在飞行中寻找目标的行为机制。鸽群优化算法由于具有收敛速度快、搜索效率高的优势,已得到广泛应用[13]。文献[14]在2014年将鸽群优化算法引入模拟退火算法思想,用于解决低空无人机目标检测问题。文献[15]在2015年将其运用在航天器的最优编队重构问题。文献[16]在2018年在线滚动时域控制中应用鸽群优化算法。但针对参数整定等多维优化问题,在鸽子的数目、寻优迭代次数较少的情况下,经典的鸽群优化算法容易出现陷入局部最优、迭代后期收敛速度过慢等问题。
本文提出了一种变权重变异鸽群优化(Variable Weighted Mutant Pigeon Inspired Optimization, VWMPIO)算法,将反向变异操作加入到地图和指南针算子中,从而降低了鸽群寻优陷入局部最优解的概率。自适应权值能够增加处于较优位置的鸽子在鸽群中的权重,相比经典的鸽群优化算法能够提高算法寻优的效率,从而提高无人机的姿态控制水平。
本文以F-16的公开数据为基础,建立无人机模型,通过MATLAB/SIMULINK进行建模仿真。仿真平台包括无人机六自由度非线性模型。本文首先根据自主空中加油的特点,基于自抗扰技术设计了姿态稳定控制器的结构。为解决人工整定参数困难的问题,获得最佳的控制效果,使用变权重变异鸽群优化算法进行寻优,并与传统的启发优化算法进行对比分析。
1 无人机六自由度数学模型
无人机通过调整升降舵、副翼和方向舵的角度,改变无人机的俯仰角、偏航角和俯仰角大小。构建无人机的六自由度运动学与动力学模型为
(1)
式中:p、q、r为无人机滚转角速度、俯仰角速度及偏航角速度;φ、θ、ψ为无人机的滚转角、俯仰角与偏航角;Ix、Iy、Iz分别为无人机绕机体轴的转动惯量;3个力矩分量为滚转力矩L、俯仰力矩M、偏航力矩N,其表达式为

(2)

无人机空中加油过程中,受油机受到加油机尾流等风干扰因素影响,同时空中加油任务的特殊性要求受油机跟踪快速运动的锥套。由于固定翼无人机系统具有欠驱动、强耦合的特点,处理好空中加油任务中控制器的控制精度与响应速度是控制器设计的难点。
2 无人机自抗扰控制器
2.1 自抗扰控制器结构设计
自抗扰控制器由跟踪微分器(Tracking Differentiator, TD)、扩张状态观测器(Extended State Observer, ESO)和非线性状态误差反馈控制律(NonLinear State Error Feedback, NLSEF) 3部分构成[17]。自抗扰控制器结构如图1所示。

图1 自抗扰控制器的结构Fig.1 Structure of ADRC controller
对于系统模型中的不确定性与外部的扰动,利用扩张状态观测器进行估计与补偿,从而抑制系统干扰。在基于自抗扰控制的无人机俯仰角、滚转角控制律以及偏航角的增稳控制律设计中采用相同的控制策略。基于自抗扰控制器的无人机姿态控制律结构框图如图2所示。将无人机姿态方程整理为符合自抗扰理论的对应形式如式(3)所示。

图2 无人机姿态控制律结构框图Fig.2 Diagram of attitude control law of UAV

(3)
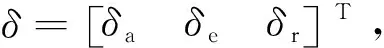
(4)
2.2 自抗扰控制器算法设计
1) 跟踪微分器
跟踪微分器的输出变量v1跟踪输入指令信号v0,输出变量v2是输出变量v1的微分。跟踪微分器的离散形式为
(5)
式中:r0为决定跟踪速度的速度因子;h0为滤波因子;h为时间步长,单位为s;fhan(·)为最速控制综合函数,表达式如式(6)所示;sign(·)为符号函数,其表达式如式(7)所示。
(6)

(7)
速度因子r0越大,跟踪器的跟踪效果就越快,反之则可以避免超调,因此选择合适的速度因子可以实现无超调的快速跟踪。滤波因子h0能够滤掉跟踪信号的噪声部分,对含有噪声或不连续的输入也可以得到平滑的跟踪信号,从而提高了系统控制的鲁棒性。对于无人机的控制来说,跟踪微分器可使控制器快速无超调地跟随指令,且输入保持连续光滑,减少无人机系统受突变指令信号的影响,从而避免机体抖振的出现。
2) 扩张状态观测器

(8)
式中:e为观测值与状态的误差量;fal(·)为非线性函数,其非线性的程度由α01、α02决定;β01、β02、β03为扩张状态观测器的增益;α01、α02一般取值为0.5与0.25,β01取值100[18]。fal(·)能够实现工程中所需要的 “小误差大增益,大误差小增益”的良好功能;δ表示其线性区间的宽度,在实际系统中,一般取为0.02 左右[6],α为幂次,反映了观测器的非线性程度。其表达式如式(9)所示。
(9)
3) 扰动补偿过程
在误差反馈控制量u0基础上,将观测到的扰动量用于补偿,控制量如式(10)所示。对扩充观测的补偿能够使得控制器实现抗扰。
(10)
4) 非线性状态误差反馈律

(11)
式中:β1、β2分别为非线性误差反馈的比例和微分的增益,相当于PID控制器中的增益参数。δ1的作用与扩张状态观测器中类似,本文取值为0.5。
在调节控制器参数时,r0、h0、β02、β03、a11、a12、β11、β12、b0等9个参数需根据系统实际需求变化。
3 变权重变异鸽群优化算法的设计
3.1 经典鸽群优化算法
鸽群算法由两个独立的迭代循环组成,在每个循环中使用不同的算子模型,模拟鸽子在飞行不同阶段使用不同的导航工具。

(12)
式中:R为地图因子;rand为数值在0到1之间的随机数;t为当前迭代的代数;Xgbest为上一次迭代中全局最好的位置。当算子循环次数达到NC1max后停止,进行下一个算子的操作。
地标算子(Landmark Operator)模仿鸽子利用地标导航的过程。地标算子如式(13)~式(15)所示更新。
(13)
(14)
Xi(t)=Xi(t-1)+rand·(Xgbest-Xi(t-1))
(15)
式中:NN为每一代中鸽子的总数;Xcentre(t)为第t代鸽子的群体中心位置;fitness(·)为鸽子所在位置的适应度函数。鸽群的数目按照式(15)更新。其中,处于适应度函数较差位置的鸽子会被舍弃。当算子循环次数达到NC2max次后,结束鸽群优化算法。
3.2 对经典鸽群优化算法的改进
鸽群优化虽然具有较快的收敛速度,当搜索范围复杂、搜索空间的维数较大时,搜索结果容易落入局部最优。为提高其在解决无人机控制问题时的精确性,本文从两个方面对经典鸽群优化模型的地图和指南针算子进行了改进。
在经典的鸽群优化公式中,权重ω=e-Rt随着时间的演化,调节鸽群的全局和局部搜索能力。受粒子群算法启发,对于复杂寻优问题,智能体间的信息共享能力比单个个体的搜寻功能更重要[19]。惯性权重高则全局的搜索能力较好,而惯性权重低能够获得局部搜索能力的加强[20]。但经典鸽群优化对所有鸽子均赋相同权重,没有考虑每只鸽子所处位置之间的差异。因此,本文设计了一种自适应的非线性有界递减权重,如式(16)所示。
(16)
式中:R和经典鸽群优化的定义相同;fitness(Xi)和fitness(Xgbset)为第i只鸽子和全局最优鸽子的适应度函数。在算法执行过程中,权重的初始值为e-R,并随着迭代连续有界下降,这与经典鸽群优化算法在初期具有较大的搜索范围、后期快速收敛的特性一致。同时,鸽子自身位置适应度函数和当前最优位置适应度函数之比反映了不同鸽子间的位置差异,用于调整权值,使得鸽群更好地收敛到最优解。
在广泛搜索的地图和指南针算子阶段,我们希望鸽子能够跳出局部最优值。对于适应度最差的鸽子,由于其与当前最优鸽子距离较远,按照经典鸽群优化算法对于寻优过程的贡献较低。因此将适应值最差的鸽子的速度设定为当前全局最优鸽子Xgbset的反方向,这样能够增加鸽群的多样性。经过反向变异操作后,鸽群提高了全局的搜索能力,更容易在前期跳出局部最优。适应值最差的鸽子的更新如式(17)所示。
(17)
无人机的控制目标是使无人机的姿态在较短时间内尽可能快速、精准地跟随指令,因此适应度函数中应当包括姿态角指令和无人机的真实姿态。本文选取时间乘绝对误差积分准则(ITAE)误差准则[21]作为优化算法的适应度函数。适应度函数的值越小,说明鸽子所处的位置越优越。用ITAE误差作为优化的适应度函数为

(18)
式中:τ为系统运行的时间;e(·)为无人机姿态角指令和真实姿态之间的误差;J为误差的评价函数,用作优化算法的适应度函数。按照本节提出的改进,本文所提出的变权重变异鸽群优化算法的流程图如图3所示。

图3 变权重变异鸽群优化算法的流程图Fig.3 Flowchart of VWMPIO
4 仿真及分析
本文使用MATLAB/SIMULINK仿真工具,搭建自抗扰控制器模型,并与经典的串级PID控制器的仿真效果比较。首先,本文测试俯仰角通道的控制性能,选取俯仰角指令的角度为5°,选取控制步长为0.02 s,并于经典PID的控制器进行比对。通过实验,选择自抗扰控制器粗调参数如表1所示。2种控制器的控制效果如图4所示。
对2种控制器分别加入等幅的高斯噪声,测试2种控制器的抗干扰能力,其输出曲线如图5所示。

表1 自抗扰俯仰控制通道粗调参数

图4 俯仰通道PID和ADRC控制器输出曲线Fig.4 Output curves of pitch channel of PID and ADRC controller

图5 干扰下的俯仰通道PID和ADRC控制器 输出曲线Fig.5 Output curves of pitch channel of PID and ADRC controller under disturbance
分析图4和图5可以发现,自抗扰控制器的过渡时间小于PID控制器,超调量也更小,对噪声的抑制效果显著。
本文使用变权重变异鸽群优化整定控制器的参数,优化的结果与粒子群优化算法及经典鸽群算法进行对比,优化算法适应度函数均采用上述的ITAE误差。对于俯仰角控制通道,对r0、h0、β02、β03、a11、a12、β11、β12、b0等9个参数进行优化,其他参数设定保持不变。首先需要对各优化算法的状态参数进行初始化操作,粒子群算法的参数如表2所示,经典和变权重变异鸽群优化的参数如表3所示。自抗扰控制器经过变权重变异鸽群优化算法的优化后,其控制性能得到了进一步的提高,各参数的迭代曲线与优化后的仿真结果如表4和图6~图10所示。

表2 粒子群算法初始参数Table 2 Initial parameters of PSO

表3 鸽群优化、变权重变异鸽群优化算法初始参数Table 3 Initial parameters of PIO and VWMPIO

表4 俯仰通道变权重变异鸽群优化前后的参数对照

图6 俯仰通道适应度函数优化曲线Fig.6 Optimization curves of fitness function of pitch channel

图7 俯仰通道r0、h0优化曲线Fig.7 Optimization curves ofr0and h0 of pitch channel

图8 俯仰通道β02、β03和b0优化曲线Fig.8 Optimization curves ofβ02, β03 and b0 of pitch channel

图9 俯仰通道a11、β11、β12优化曲线Fig.9 Optimization curves ofa11 andβ11 and β12of pitch channel

图10 ADRC控制器优化前后输出曲线Fig.10 Output curves of ADRC controller before and after optimization
对比变权重变异鸽群优化算法与粒子群算法、普通鸽群优化算法的优化结果,变权重变异鸽群优化算法在寻优的早期阶段可以快速收敛,且最终收敛的位置比粒子群算法和普通鸽群优化算法要优越。
本文接下来优化横滚和偏航通道参数。仿照俯仰角通道的优化,同样选取控制周期为0.02 s,优化算法的初始鸽群参数如表2和表3所示。设定滚转角指令角度为5°,滚转角控制通道跟随指令,控制回路偏航角通道为无人机的横侧向运动进行增稳。各优化算法的初始状态参数与俯仰通道保持一致,优化前后的参数分别如表5,参数对比曲线如图11~图18,仿真结果如图19所示。

表5 横滚、偏航通道变权重变异鸽群优优化前后参数对照

图11 横滚通道适应度函数优化曲线Fig.11 Optimization curve of fitness function of roll channel

图12 横滚通道r0、h0优化曲线Fig.12 Optimization curve ofr0and h0 of roll channel

图13 横滚通道β02、β03和b0优化曲线Fig.13 Optimization curve ofβ02, β03 and b0 of roll channel

图14 横滚通道a11、β11、β12优化曲线Fig.14 Optimization curve of a11, β11 and β12 of roll channel

图15 偏航通道适应度函数优化曲线Fig.15 Optimization curve of fitness function of yaw channel

图16 偏航通道r0、h0优化曲线Fig.16 Optimization curve of r0 and h0 of yaw channel
横滚和偏航通道的控制结果得到了一定的改善,横滚和偏航通道的结果验证了本文提出的算法的可行性。

图17 偏航通道β02、β03和b0优化曲线Fig.17 Optimization curve of β02, β03 and b0of yaw channel

图18 偏航通道a11、β11、β12优化曲线Fig.18 Optimization curve of a11, β11 and β12 of yaw channel

图19 ADRC优化前后和PID控制器控制效果对比Fig.19 Output curve of ADRC controller before and after optimization and PID controller
5 结 论
1) 本文设计了一种基于自抗扰控制技术的无人机的姿态增稳控制器。利用F-16模型进行了仿真实验,与经典的PID控制算法对比,本文设计的自抗扰控制器的控制精度较高,对噪声和扰动有着较好的抑制效果。
2) 与传统的优化算法相比,本文所设计的变权重变异鸽群优化算法保持了鸽群优化快速收敛的优点,并能够有效降低优化陷入局部最优的概率,且该算法容易实现,可提高无人机姿态控制的性能。

