高中古典概型的交汇命题教学实践与反思

杨 莹

（福建省三明市第二中学，福建三明 365000）

引 言

概率是高中数学的重点内容。新课程改革以来，概率在高中数学的地位日益重要，它不仅有利于培养学生的数学应用能力，而且也是学生在高等数学学习中必不可少的基础知识。古典概型是一种特殊的数学模型，也是最基本的概率模型。它的引入避免了大量的重复实验，得到的是概率的准确值。笔者在实际教学工作中发现，许多学生在解答与古典概型有关的题型时常常因不得要领而发生错误，为此，研究近年来高考中有关古典概型的考题，发现考题背景新颖、设问巧妙，且常在与其他数学知识点，如平面向量、立体几何、函数、统计等知识网络交汇处设计试题。

一、古典概型与平面向量的交汇命题

对古典概率与向量交汇的考查是高考常考命题之一，可将古典概型与平面向量的平行与垂直及坐标表示、平面向量坐标运算等基础知识有机结合。案例中使成立的(m,n) ，满足mn=−2 ，所以事件A 发生的情况有（-2，1），（-1，2），（1，-2），（2，-1），所求的概率为：使成立(m,n) 的条件满足m(m− 4) + 2n+ 1 =0，即m2− 4m=−1 −2n，事件B 发生的情况有（1，1），故所求概率为：。解此类问题，要先根据平面向量的知识进行坐标运算，得出事件满足的约束条件，再根据约束条件（等式或不等式）列举出所有符合条件的结果，最后利用古典概型的概率计算公式求解概率。特别注意的是，用列举法列出事件的所有可能结果时，要按一定的顺序，避免重复、遗漏。

二、古典概型与统计的交汇命题

案例：清明节期间，高速公路车辆较多，某调查公司研究了服务区中七座以下的小型汽车，按进服务区的先后每间隔50 辆就抽取一辆的抽样方法，抽取40 名驾驶员进行调查，将他们在某段高速公路的车速（km/h）分成6 段：（60，65）、[65，70）、[70，75）、[75，80）、[80，85）、[85，90）后得到如图1 所示的频率分布直方图。

（1）该公司在调查取样中用的是哪种抽样方法？

（2）若从车速在[60，70）的车辆中任取2 辆，求抽出的2 辆车的速度在[60，65）和[65，70）中各1 辆的概率。

对古典概率与统计交汇的考查是高考常考命题之一，其考点丰富，难度适中。此类题从考查统计的基础知识入手，侧重考查学生分析数据的能力，具有一定的综合性与灵活性。本案例考查了系统抽样和频率分布直方图等基本知识。解此类问题，重点要先分析相关数据，如频率分布直方图的有关特征问题，再用古典概型公式计算。易错点是用列举法列出事件所有的可能结果时没有按一定顺序而出现遗漏。

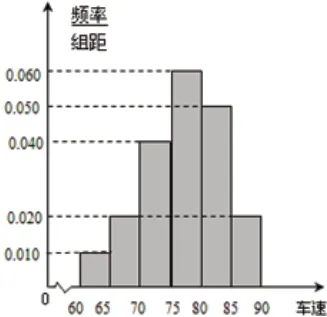
图1 频率分布直方图

三、古典概型与立体几何的交汇命题

案例：如图2 所示，从A1(1，0，0)、A2(2，0，0)、B1(0，1，0)、B2(0，2，0)、C1(0，0，1)、C2(0，0，2)这6 个点中随机选取3 个点，

（1）求这3 点与原点O恰好是正三棱锥四个顶点的概率；

（2）求这3 点与原点O共面的概率。

高考中这一类型的交汇命题属于中难题型，题型新颖，综合性强，巧妙地将古典概型与立体几何知识合理融合，既有趣味性，又考查了学生将二者综合分析的能力，对学生的思维能力要求较高。求解此类问题，应先利用立体几何知识求出基本事件总数和满足条件的事件数，再利用古典概型公式计算求得。在求一些较复杂的基本事件个数时，还可以利用排列组合知识解决问题，或者先求其对立事件的概率，进而再求解。案例中，从这6 个点中任取3 个点分三类：在x 轴上取2 个点、1 个点、0 个点，共有＝20 种取法，选取的3 个点与原点O恰好是正三棱锥顶点的取法有2 种，概率第二小题根据立体几何知识有两种方法。方法一：选取的3 个点与原点O共面的取法有＝12 种，所求概率为方法二：选取的3 个点与原点不共面的取法有＝8 种，这3 个点与原点O共面的概率

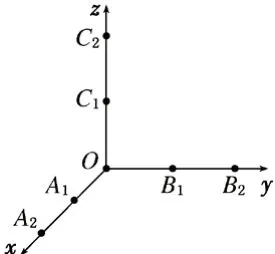
图2

四、古典概型与函数相结合

高考中，函数知识的命题属于中难题型。这类问题将函数知识融入概率相关知识，形成新的命题情景，加大了对学生的考查力度。解此类问题，要根据函数的相关性质，确定相关系数应满足的条件，如f(x)＞b恒成立，可转化为，再根据系数满足条件分类考虑，求出所有符合条件的基本事件个数，即事件A 包含：（1，2），（1，3），（2，2），（2，3），（2，4），（2，5），（3，2），（3，3），（3，4），（3，5）共10 个，最后利用古典概型概率计算公式求解概率得

结 语

古典概型作为一种知识媒介，可以和高中数学中的许多知识进行交汇[1]。除了以上四种情况，它还可以和不等式、数列、集合等知识“联袂出演”，创设出新的命题情境。整合后的命题综合性得到进一步加强，有利于提高学生学习的系统性、综合思维能力，这体现了高考题注重双基和能力的宗旨。教师在教学中应该注重古典概型的概念教学。只有学生真正地深刻理解了基本概念，掌握了思想方法，才能有效提高学生的应用能力，灵活解决位于知识网络交汇处的问题。