正逆双向思维在三维地质建模课程教学中的应用探讨

梅钢，徐能雄

(中国地质大学（北京）工程技术学院，北京)

一 引言

自然界的地质现象是多种多样的，由于地质发展和环境的差异，导致大部分的地质现象都具有一定的复杂性，地质研究者往往通过地质勘查和对应的分析来了解地质特征，同时建立抽象的数据轮廓。随着计算机技术的发展，人们希望更加立体和真实的认识地质现象，正是在这种背景下，三维地质建模技术应运而生，并且经过十几年的发展，三维地质建模技术已经在实践和理论方面都得到了很大的成就。

三维地质建模[1]技术涉及到多个学科，如地质学、数学地质、几何学、拓扑学与计算机图形学等领域的相关理论、方法与技术。三维地质建模[9]方法包括地质勘探数据的标准化处理、几何造型、三维空间数据模型，属性数据管理与图形可视化等方面。由于方法体系涵盖内容广泛，知识的跨越性大，阻碍了这项技术的实现与推广。研究生对地质知识点的理解，可以通过三维地质模型得到加深，三维地质模型不仅让地质教学变得更加生动有趣，同时也让课堂效率得到了极大的提高。三维地质建模课的主要目的是将三维地质建模的基础方法及其相应的算法与程序呈现给学生，通过算法和程序的学习，使学生能够学以致用，自己编写三维地质建模的算法和程序，从而为以后的工作和研究做准备。

由于三维地质建模课程具有多学科交叉的特点，所以学生针对复杂建模问题和算法的理解是这门课程的主要瓶颈。大部分学生在遇到复杂建模问题和算法时，往往倾向于从自己习惯的角度去寻找解决方法，这样虽然省去一些思考时间，但有时会限制解题思路，很多情况下学生的解决方案不尽人意。因此建立与三维地质建模相适应的教学方法成为一个值得探讨的问题。正逆双向思维是一种广泛应用于各个领域的思维方式，在教学和学习过程中，面对不同的问题，运用不同的方法去思考，可以激发学生的灵感和创造性思维。正逆双向思维是一种不可低估的创造性思维，它可以帮我们化解问题，使我们能够抓住主要矛盾，提高对问题的理解能力。

本文运用正逆双向思维的教学手段，以转换问题思考角度和解决手段为着力点，深度剖析两个三维地质建模经典算法案例，帮助学生快速准确理解三维地质建模的难点问题。

二 正逆双向思维及逆向思维的应用

正逆双向思维主要分为正向思维方式和逆向思维方式。正向思维一般是指人在长期学习生活中形成的一种惯性思维，在遇到新问题时，人们往往会倾向于选择这种对于自己更加熟悉和自然的思考方法；逆向思维是指人们跳出思维舒适区，打破思维定式，从反方向来思考问题的一种思维方式，逆向思维更强调思维的发散性与创新性。在三维地质建模教学时，教师应多角度地、全方位地、辩证地进行分析不同的三维地质建模问题，否则学生容易以偏概全，形成错误的三维地质建模概念，而正逆双向思维很好的解决了这一问题。正向思维方式主要针对简单问题，逆向思维主要针对较难理解的复杂建模问题，本文主要对逆向思维做详细论述。

逆向思维是一种将习以为常的事物反过来思考的思维方式，它不仅对我们的日常生活产生了积极的影响，而且在各个领域有着不可忽视的作用。在数学领域中，恰当地运用逆向思维可以化繁为简，化难为易，甚至可以解决许多利用常规思维难以解决的问题[2,3]；在新闻采写中，利用逆向思维提高新闻采写质量[4]；在化学教学中，常利用逆向思维来解决计算中的复杂问题[5]等。

常见的逆向思维有三种，分别是反转型逆向思维、转换型逆向思维和缺点型逆向思维。反转型逆向思维是从事物的因果关系反方向推导的一种思维方式，一般用于解决正向思考较为复杂的科学问题，最常见的方法就是反证法，反转型逆向思维的针对性较强，要求学生充分理解问题的充分和必要条件。转换型逆向思维是指在解决问题时常用的手段受阻而尝试转换思考方式或解决手段的一种思维方式，转换型逆向思维要求学生活跃思维，不拘泥于特定的思维定式。缺点型逆向思维是指合理利用事物的缺点，化不利为有利的一种思维方法，这种方法并不以克服事物的缺点为目的，相反，它是将缺点化弊为利，找到解决方法。在三维地质建模课程中，我们常用的逆向思维方法是反转型逆向思维和转换型逆向思维。

逆向思维有以下三个特点[2]：(1)普遍性。心理学上研究发现人的思维不是单向的，一个特定的思维过程一般来说都会有一个相应的反向思维过程，因此很多领域都存在着逆向性思维，如数学、物理、广告、设计等。(2)批判性。在日常学习工作中，我们往往习惯以常规的正向思维去思考解决问题，而逆向思维正好和其相反，是对我们习以为常的惯例或常识进行挑战，也就是逆向性思维具有批判性。(3)新颖性。我们常用的思维方式虽然简单高效，却容易使思维呆板，还会妨碍思维的发展。运用逆向思维思考问题可以一定程度上消除这种障碍，得出许多新颖的创造性的结果，给人眼前一亮的感觉。

三 正逆双向思维在三维地质建模课程教学中的应用

地质现象和事物是非常复杂的，所以在教学中，能全方位、多角度辩证的分析地质现象就变的尤为重要，否则学生容易形成片面理解和错误的地质概念。而用正逆双向的思维方式进行教学，很好的解决了学生对地质问题单一理解的思维模式。所以正反双向思维的教学方式不仅可以提高教学趣味，而且有助于学生对问题形成比较全面的认识，最后使学生的认识水平得到升华。总之，用正逆双向的思维模式进行教学，在多个学科中已经得到了应用，并且得到了积极的教学反馈，所以正逆双向的思维教学方法具有普遍适用性[6]。

插值是三维地质建模重要的研究领域之一。由于工程钻探的成本较高，在一个特定的研究领域钻孔的数量是有限的，直接使用原始的钻探数据进行地质建模不可能构建出精确的实体模型。因此，需要通过采用插值技术对我们得到的原始钻探数据进行加密，进而得到能够构建出满足需要的实体模型。原理上，插值是通过已知采样点计算未知采样点值的技术。IDW、趋势面插值、Kriging、样条插值等多个插值目前被广泛运用在多个领域。本文将以IDW[7]和Kriging[8]为例，探讨正逆思维在三维地质建模中的应用。

（一）运用正向思维理解IDW 插值算法

IDW 插值方法常作为课堂插值教学的第一个例子，因为其原理简单，且算法学生容易动手实现，IDW 在插值后能够保留原样点的真值，所以在离散点空间分析中也常被应用。IDW 插值算法是基于相近相似的原理，即距离插值点越近的采样点对插值点的影响就越大，距离插值点越远的采样点对插值点的影响就越小，当采样点距离插值点无穷远时，采样点对插值点的影响很小，并几乎趋近于0。以一个待插值点p(x,y)和三个采样点p1(x1,y1)、p2(x2,y2)、p3(x3,y3)为例，详细推导。推导过程如下：

第一步是计算每个采样点和待插值点的距离

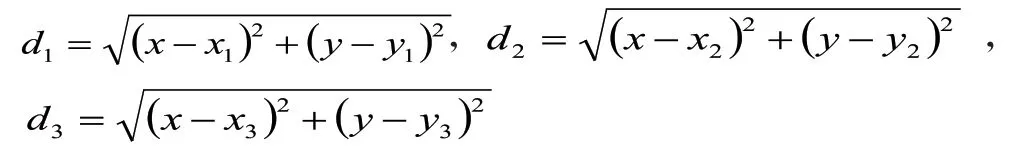
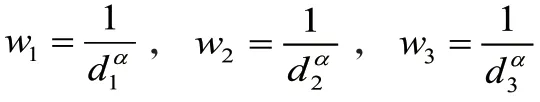
为了求得插值点的属性值，将每个采样点的属性值赋予一定的权重然后求和，即，展开得到：

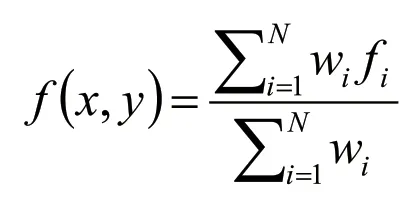
基于以上推导，将此方法类比到N 个采样点，就能得到一般的IDW 插值计算公式：

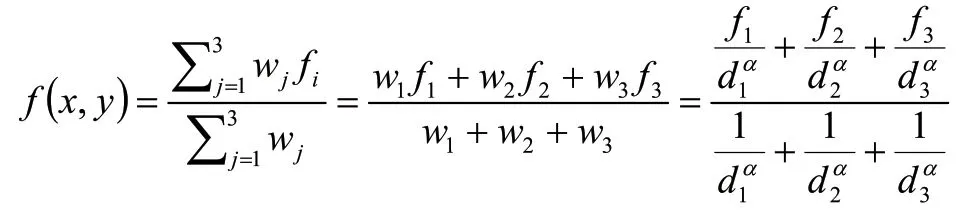
从以上对IDW 插值的一般过程的推导，可以看到这是一个原理比较简单的插值算法，因此对于形式简单的IDW 插值，一般课堂教学采用正向思维的方式进行讲解。

（二）运用正逆双向思维解析克里格插值算法

相比于IDW 插值，Kriging 插值在形式和数学原理上更加复杂。为了使学生充分理解Kriging 插值算法，需要用逆向思维的方式引导学生并为学生讲解。

空间连续性变化的属性往往是不规则的是Kriging 插值方法的主要观点，并且地理统计的思想也在Kriging 插值方法中体现出来。由于平滑的数学函数对Kriging 插值方法简单模拟的误差较大，所以在对空间场进行预测时，一般会将空间场视为随机场。Kriging 插值的算法流程图如图1 所示。

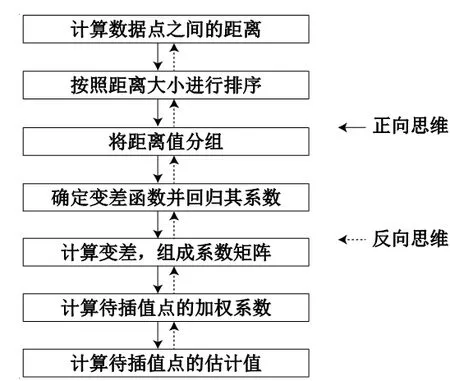
图1 Kriging 法的算法流程图

从Kriging 插值算法流程图看出Kriging 插值的计算过程从正向理解比较复杂，且目的性不够明确，在有限的课堂教学时间内，让学生充分理解Kriging插值算法存在一定难度。但是，如果运用逆向的思维方式进行讲解，Kriging 插值算法中每一步推导过程的目的性就会较为明确，学生也会更容易理解。以下运用逆向思维对Kriging 插值进行讲解。

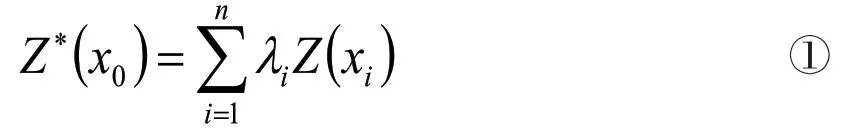
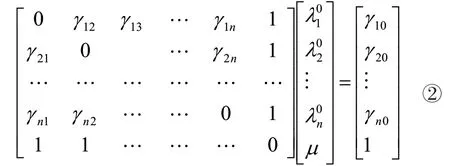
3.线性方程组的系数矩阵和右侧的列向量根据变差函数γ(h)的表达式进行组装，要得到变差函数γ(h)的表达式，需要进行函数拟合，选择一定的变差函数理论模型，并求出模型参数。

4.拟合变差函数γ(h)的表达式的过程需要根据式③变差函数γ(h)的估计值γ*(h)的计算理论。

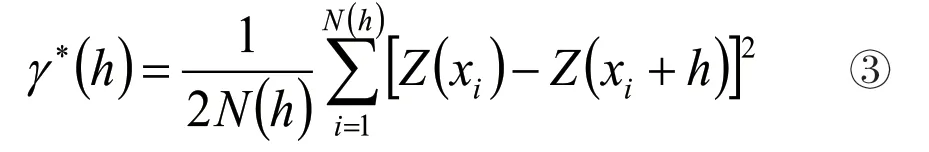
5.计算理论变差函数γ(h)的估计值γ*(h)，需要将所有各测量点之间的距离按照由小到大的顺序分组。

从结果出发，需要求什么，我们就去计算什么，这样学生就能很直观的理解为什么这么计算。从步骤1 到步骤5 可以明显感觉到运用逆向思维的讲解模式，从结果出发，求解过程中遇到未知量，再去求解未知量，即带有目的性的去求解，这样的讲解模式增加了学生对问题的直观理解，使学生从多方位思考问题和掌握解决问题的方法。

（三）逆向思维在三维地质建模课程中对提高教学质量的作用

三维地质建模方法是若干理论、方法与技术的集合体，具有多学科交叉融合的背景。传统的三维地质建模课堂教学模式都是以教师讲解理论知识和原理为主，没有深入推导验证关键算法，导致学生对建模相关的算法的原理理解不够透彻，进而可能导致学生无法建立理想的三维地质模型。

本课程将正逆双向的思维授课模式与三维地质建模授课相结合，将课程中的复杂插值方法化繁为简，化难为易，帮助学生抓住主要矛盾，使学生掌握教学大纲的重要知识点，更重要的是引导学生积极思考和创新，提高学生解决复杂问题的能力。

四 结语

三维地质建模是一门多学科交叉的课程，它不仅需要一定的地质基础知识，也需要对编程算法有一定的认识，所以学生针对复杂建模问题和算法的理解是这门课程的主要瓶颈，而正逆双向的思维方式可以帮我们把认为难以理解的教学例子变得简单，大大提高课堂效率，所以将正逆双向思维运用在三维地质建模课程上，不仅可以帮助学生理解复杂地质三维建模问题和算法，还有助于学生思维方式的转变，使学生在将来遇到问题时，可以多方位剖析问题。因此，在三维地质建模这门课程授课过程中，教师适当的运用正逆双向的教学手段，有意识的引导学生运用正逆双向思维方式分析，这将对学生以后创新能力和解决问题能力提高都大有裨益。