对一道高考概率压轴题的思考与拓展

汪 乐 张启兆

近年来，高考数学试题正从能力立意到素养导向发展,同时，压轴题不再拘泥于传统的数列、导数等问题,2019年高考全国卷Ⅰ理科数学的压轴题就是一道概率题，本文就对这道概率压轴题进行分析与拓展．

1 原题呈现

例1(2019年全国卷Ⅰ) 为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.

(1) 求X的分布列;

(2) 若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.

(ⅰ) 证明: {pi+1-pi}(i=0,1,2,…,7)为等比数列;

(ⅱ) 求p4,并根据p4的值解释这种试验方案的合理性.

2 思维障碍

许多同学一见到此题,就被“吓住”了:文字信息多,数据多,做题的信心也就不那么足了!笔者分析主要会在如下5个方面存在问题.

1) 审题时不会抓关键词．如“若都治愈或都未治愈则两种药均得0分”,有部分学生将“若都治愈”忽略掉了,从而在计算P(X=0)时出现了错误.

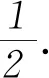
3) 数据分析的能力有待提高．如第(2)问中给出了一些数据,但部分同学不会分析,想不到利用第(1)问的结论把a，b，c先求出来,然后代入pi=api-1+bpi+cpi+1(i=1,2,…,7),从而得到0.5pi=0.4pi-1+0.1pi+1．

4) 缺乏解题经验的积累．这种综合题,通常“没有白做的前一问”,即前一问常常为后一问“铺路搭桥”．由于缺乏这种意识,第(2)问(ⅱ)没想到利用前一问得到的pi+1-pi=p1·4i-1(i=0,1,2,…,7),从而无法联想到“等差数列”和“累加法”,进而不知道利用方程思想解决问题．

5) 不会分析试验方案的合理性，特别是有些学生对概率的意义不理解． 在本题中，若不了解假设检验的统计思想和基本概念，就不会根据p4的值解释这种试验方案的合理性．

3 解法剖析

1) 阅读理解, 寻求突破.

在阅读过程中要学会抓关键词．本题的关键信息有如下4点.

a)当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效;

b)对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分;

c)甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X;

d)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.

第(1)问的目标是求X的分布列,因此先要明确:X表示一轮试验中甲药的得分,X的取值有3种情况，即1，-1，0.得1分是施以甲药的白鼠治愈且施以乙药的白鼠未治愈,则P(X=1)=α(1-β);得-1分是施以乙药的白鼠治愈且施以甲药的白鼠未治愈,则P(X=-1)=(1-α)β;得0分是都治愈或都未治愈,则P(X=0)=αβ+(1-α)(1-β)．

第(2)问(ⅰ)要证明: {pi+1-pi}(i=0,1,2,…,7)为等比数列;第(2)问(ⅱ)求p4,并根据p4的值解释这种试验方案的合理性.由于第(2)问直接给了数列的递推式,因此顺着题目要求,利用题目中所给的“脚手架”,问题就容易突破了．

2) 化归整合, 提炼题目.

在阅读过程中学会“翻译”,把文字语言“翻译”成对应的数学语言．如:随机分配一只小白鼠试验甲药,随机分配一只小白鼠试验乙药(隐含的条件就是试验是独立的),一轮试验共有4个可能出现的结果(每一个结果即为一个样本点)，如表1所示.

表1

(这里符号√,×分别表示治愈和未治愈)

又如:一轮试验会反复进行,即独立重复试验,什么时候结束呢?如何将已知条件“当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验”翻译为数学语言?

当问题比较抽象的时候,可以运用特殊化法和枚举法帮助我们理解题目，如表2所示．

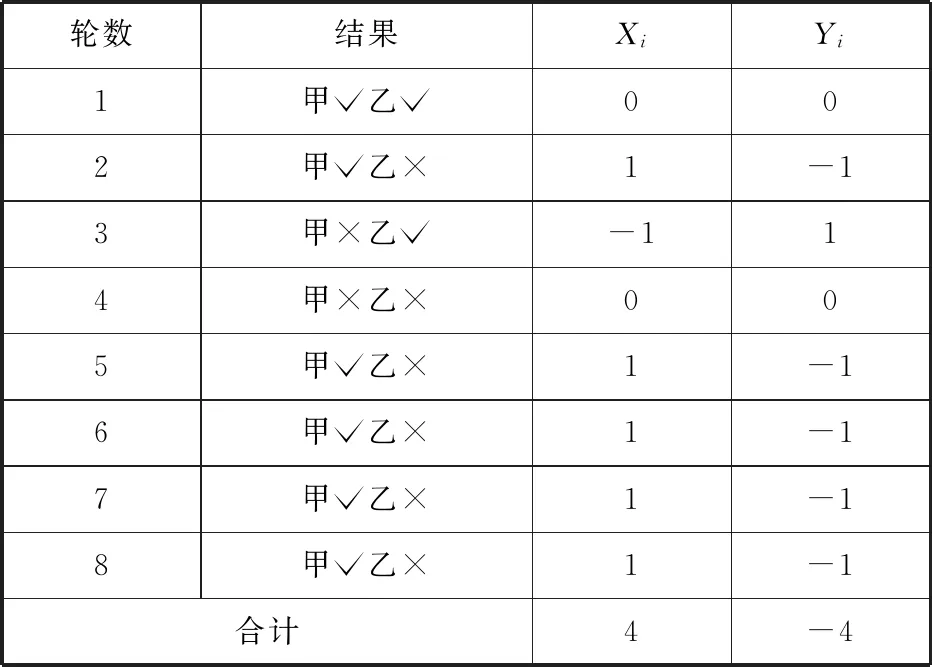
表2

从表2中,我们不难发现，因为Xi=-Yi,所以 ∑Xi=-∑Yi;当且仅当∑Xi=4 或-4时试验结束．这样就把“当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验”翻译为数学语言了．即当∑Xi=4时，认为甲药更有效,当∑Xi=-4时，认为乙药更有效．

3) 追本溯源, 梳理知识.

通过联想,找到与问题信息相关的知识、解题技巧以及对相关数学符号、概念、命题等的理解,识别出问题类型.如本题在分析已知条件后，需要联想到随机试验、独立重复试验、离散型随机变量的分布列及其概念,同时，要掌握证明等比数列的基本方法、数列的递推关系等．

本题中试验的思路和各类比赛记分方法相似，以乒乓球比赛为例,甲、乙进行乒乓球比赛,三局两胜制.每局比赛中,如果甲至少得到11分且至少领先乙2分才能获胜,也就是说甲以11∶9，12∶10，13∶11，14∶12…比分领先才算获胜．这里看的是净胜球,不是得分比例．这道题题干中相当于把甲至少得到11分且至少领先乙2分换成了甲至少得到4分且至少领先乙4分．有了这个模型,第(1)问的解题思路就有了．

由第(2)问(ⅰ)要联想到数列的递推关系和“差数列”模型,从而联想到“累加法”,p4的值就容易求出了．

4) 水到渠成, 得出结论.

解析 (1)X的所有可能取值为1，-1，0.

得1分是施以甲药的白鼠治愈且施以乙药的白鼠未治愈,则P(X=1)=α(1-β);

得-1分是施以乙药的白鼠治愈且施以甲药的白鼠未治愈,则P(X=-1)=(1-α)β;

得0分是施以甲药和施以乙药的白鼠都治愈或都未治愈,则P(X=0)=αβ+(1-α)(1-β).

综上，X的分布列如表3所示.

表3

(2) (ⅰ)因为α=0.5,β=0.8,则

a=P(X=-1)=0.4,b=P(X=0)=0.5,
c=P(X=1)=0.1.

故可得pi=0.4pi-1+0.5pi+0.1pi+1,则

0.4(pi-pi-1)=0.1(pi+1-pi),

①

(ⅱ) 由(ⅰ)知,等比数列 {pi+1-pi}(i=0,1,2,…,7)的首项为p1,那么

p8-p7=p1×47,
p7-p6=p1×46,
…
p2-p1=p1×4.

以上式子两边同时相加,得p8-p1=p1×(47+46+…+4),则

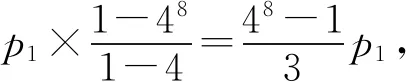
p4-p1=p1×(4+42+43),

p4表示“甲药治愈的白鼠比乙药治愈的白鼠多4只,且甲药的累计得分为4”，即最终认为甲药更有效的概率.

4 变式拓展

例2有人玩掷骰子移动棋子的游戏,棋盘分为A,B两方,开始时棋子放在A方,根据下列规定移动棋子:① 骰子出现1点时,不能移动棋子;② 出现2,3,4,5点时,把棋子移向对方;③ 出现6点时,如果棋子在A方,则不动,如果棋子在B方,则移至A方,将骰子掷了n次后,棋子仍在A方的概率记为Pn．

(1)求P1,P2;

(3)求Pn．

解析 (1)P1为将骰子掷了1次后,棋子仍在A方的概率;P2为将骰子掷了2次后,棋子在A方的概率.

这两道概率问题将概率知识与数列知识有机结合,并且问题贴近生活,体现出数学知识在解决实际问题中的价值和作用.例1对高考复习具有导向作用,能看出高考数学压轴题不再拘泥于传统的数列、导数等问题,凸显出试题正从能力立意到素养导向转变．因此,在今后的学习中,同学们不仅要重视“四基”(基础知识、基本技能、基本思想、基本活动经验),还要重视数学知识和方法在解决问题中的应用,重视数学阅读能力的培养,提高解答实际数学问题的能力.同时，要学会冷静思考,顺着问题的要求进行思考,思路中断时不妨问自己:“前一问对后一问有辅助作用吗?”要学会利用题目本身为我们搭好的“脚手架”,学会拾级而上,就能以不变应万变,在高考中取得理想成绩．