几何光学问题分类剖析
张大洪
光学是人教版高中物理教材《选修3-4》中的一个板块,也是高考的必考内容,现对近几年高考中涉及的几何光学问题进行分类剖析.
1 简单的折射光路计算问题
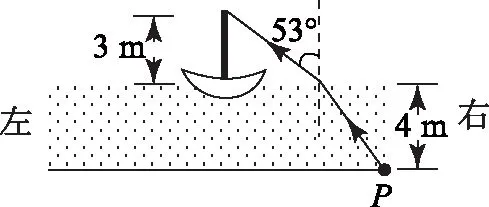
图1

(1)求桅杆到P点的水平距离;
(2)船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍然照射在桅杆顶端,求船行驶的距离.

点评 对于单纯光的折射情况,按题目要求正确作出光路图,正确理解折射率公式中与光传播方向对应的相关角度(入射角、折射角),再利用几何关系及折射率公式即可顺利解题.
2 光在等边三棱镜中的折射问题
例2(2018年全国卷Ⅲ) 如图2-甲所示,某同学在一张水平放置的白纸上画了一个小标记“·”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上,D位于AB边上;过D点作AC边的垂线交AC于F,该同学在D点正上方向下顺着直线DF的方向观察,恰好可以看到小标记的像;过O点作AB边的垂线交直线DF于E,DE=2 cm、EF=1 cm.求三棱镜的折射率.(不考虑光线在三棱镜中的反射)
解析 过D点作AB边的法线NN′,O点发出经过D点的光线即为OD,其在D点的入射角∠ODN=α,设该光线在D点的折射角为β,如图2-乙所示.根据折射定律
①
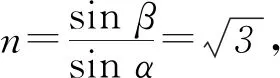
点评 对于光线经过等边三棱镜折射的情况,按题目要求和题意正确作出光路图是解题的关键.本题抓住等边三角形的特殊角,利用几何关系找准入射角与折射角,正确理解折射率公式中与光传播方向对应的相关角度即可顺利解题.
3 光在圆球形介质中的折射、反射问题
例3(2017年新课标卷Ⅰ) 如图3-甲所示,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高为2R的圆柱体,圆柱体底面镀有反射膜.有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R.已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射).求该玻璃的折射率.

图3
解析 根据球体的对称性及光路的可逆性,要使平行于中心轴OC从半球面射入的光线最后从半球面射出时恰好与入射光线平行,则只能使光线经过球面第一次折射后恰好经过底面的C点,其完整的光路如图3-乙所示.设此光线在半球面的入射角为i,折射角为r,由折射定律得
①
由几何关系知
sini=0.6, cosi=0.8,
②
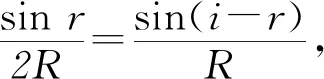
sinr=2(sinicosr-cosisinr).
③
将式②代入式③解得
④
将式②④代入式①得玻璃的折射率
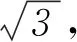
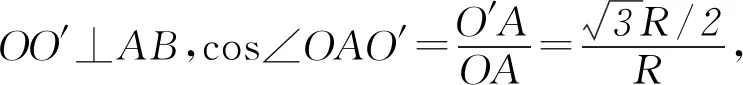
得r=30°,因而折射光线MN必垂直平分半径OA,且光线在N点对AB面的入射角∠MNE=30°,利用反射定律作出光路图如图4-乙所示,因MN垂直平分OA且∠MNA=∠MNO=60°,知反射光线NO必经过球心O点,那么反射光线NO再次经过半球面时的入射角为0°而将沿直线射出.由图可知MA∥NE且∠ONE=30°,故该光线从球面射出的方向即NO相对于其初始入射方向的偏角
θ=180°—∠ENO=150°.
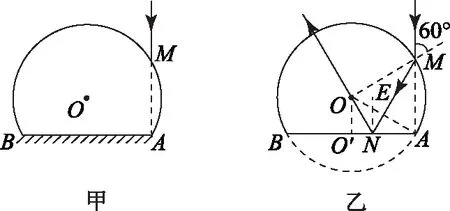
图4
点评 对于光线经过圆球形光学元件折射的情况,抓住球的对称性及半径与法线的相关性,据题意正确作出光路图是解题的关键.例3、例4充分应用平面几何知识准确找出入射角、折射角、反射角及其相互之间的关系,利用折射率公式、三角函数相应关系(如正弦定理等)进行分析处理.
4 光的全反射与平面几何知识关联问题
4.1 全反射位置不明确的探究类问题


图5

①
又由于临界角为r,则折射率为
②
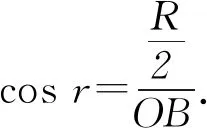
点评 对于可能发生全反射的问题需注意以下几点: 1) 明确光线传播的方向及将要经过的各个界面;2) 判定是否发生全反射,讨论发生全反射的可能范围;3) 完整分析并作出不同区域的光线经过各界面的传播光路图,找到所求区域;4) 正确作出必要的辅助线,充分运用平面几何、三角函数等知识,找准入射角、反射角、折射角,关注光的传播方向并正确运用折射定律完成解答.

图6
例6如图6所示,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线).已知玻璃的折射率为1.5,现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线).求:
(1) 从球面射出的光线对应的入射光线到光轴距离的最大值;
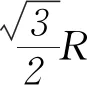



图7
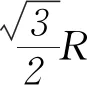
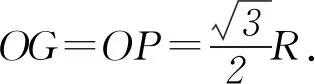
4.2 有明确的全反射位置问题
例7(2018年全国卷Ⅱ) 如图8所示,△ABC是一直角三棱镜的横截面,∠A=90°、∠B=60°,一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出.EG垂直于AC交BC于G,D恰好是CG的中点.不计多次反射.
(1) 求出射光相对于D点的入射光的偏角;
(2) 为实现上述光路,棱镜折射率的取值应在什么范围?
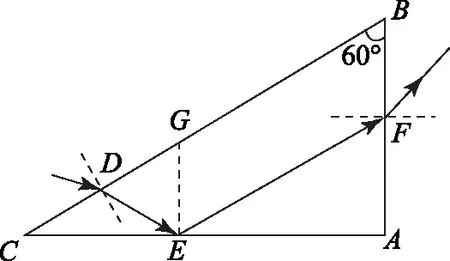
图8


图9
结合上述分析可得i2=r2=60°,r1=i3=30°,i1=r3;再由几何关系得F点的出射光相对于D点的入射光的偏角为δ=β+α,其中α=r3-i3,由三角形内角和等于180°可得β=180°-(i2+r2)-(i1-r1),再结合相应的角度值可得δ=60°.

点评 对明确发生全反射位置类问题应注意以下几点: 1)正确认识并读懂光路图;2)正确作出必要的辅助线,充分运用平面几何、三角函数等知识,找准入射角、反射角、折射角;3)准确运用光在相应界面处的折射定律(注意光的传播方向及对应公式中的角度)与反射定律完成解答;4)对于物理量的范围问题,要抓住产生此范围的原因,再利用相关数学知识进行有效处理.
5 不同色光(不同频率的光)在同种介质中的折射、全反射作图类问题

图10
例8虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明.两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图10所示.M、N、P、Q点的颜色分别为( ).
A. 紫、红、红、紫
B. 红、紫、红、紫
C. 红、紫、紫、红
D. 紫、红、紫、红
解析 白光中的可见光部分从红到紫在同一介质中的折射率大小关系为n紫>n红,由折射定律知紫光的折射角较大,由光路可知紫光将到达M点和Q点,而红光到达N点和P点,故选A.
点评 不同频率的色光在同种介质中的折射率与偏折程度不同,在可见光中从红光→紫光:光的频率增大、在同一介质中的折射率增大、偏折角增大、传播速度减小、产生全反射的临界角减小.注意根据折射定律、反射定律正确作出光路图来分析处理.
6 光的折射实验类
例9(2016年四川卷) 某同学通过实验测定半圆形玻璃砖的折射率n.如图11-甲所示,O是圆心,MN是法线,AO、BO分别表示某次测量时光线在空气和玻璃砖中的传播路径.该同学测得多组入射角i和折射角r,作出sini-sinr图象如图11-乙所示.则( ).
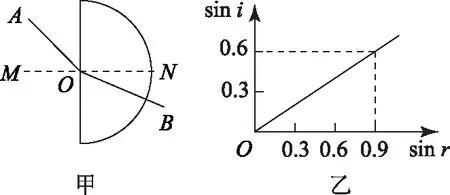
图11
A. 光由A经O到B,n=1.5
B. 光由B经O到A,n=1.5
C. 光由A经O到B,n=0.67
D. 光由B经O到A,n=0.67

点评 测定介质折射率实验中,需正确作出光路图并深入理解折射率公式中的相应角,若涉及图线则要准确挖掘图线中的各种信息,并正确分析、理解其意义.
7 光束与微小实物粒子产生经典相互作用类问题

图12
例10(2016年北京卷) 激光束可以看作是粒子流,其中的粒子以相同的动量沿光传播方向运动.激光照射到物体上,在发生反射、折射和吸收现象的同时,也会对物体产生作用.光镊效应就是一个实例,激光束可以像镊子一样抓住细胞等微小颗粒.一束激光经S点后被分成若干细光束,若不考虑光的反射和吸收,其中光束①和②穿过介质小球的光路如图12所示,图中O点是介质小球的球心,入射时光束①和②与SO的夹角均为θ,出射时光束均与SO平行.请在下面两种情况下,分析说明两光束因折射对小球产生的合力的方向.
(1) 光束①和②强度相同;
(2) 光束①比②强度大.
解析 (1) 因不考虑光的反射和吸收,仅考虑光的折射,设t时间内每束光穿过小球的粒子数为n,每个粒子动量的大小为p,以该束粒子流为研究对象,则这些粒子进入小球前的总动量为p1=2npcosθ(因①②具有对称性,故在竖直方向的总动量为0),方向沿SO水平向右;由于光在同种介质中的传播速度是相同的,即光束中的粒子在经过介质小球前、后的动量大小必均为p,故t时间内从小球射出后粒子流的总动量必为p2=2np,且方向沿SO水平向右;对这束粒子(粒子数为n)根据动量定理有Δp=p2-p1=F·Δt=2np(1-cosθ)>0,故小球对这些粒子的作用力F的方向必沿SO向右,再根据牛顿第三定律得两光束对小球合力的方向必沿OS向左.

图13
(2) 建立图13所示的xOy坐标系,在x方向:根据(1)同理可得两光束对小球的作用力必沿x轴负方向;在y方向,设t时间内光束①穿过小球的粒子数为n1,光束②穿过小球的粒子数为n2,因光束①比②强度大,即n1>n2,这些粒子进入小球前的总动量为p1y=(n1-n2)psinθ>0,即其方向竖直向上(y轴正方向);从小球出射时y方向的总动量p2y=0.根据动量定理得
Fy·Δt=p2y-p1y=-(n1-n2)psinθ,
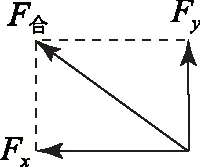
图14
可知小球对这些粒子的作用力Fy的方向沿y轴负方向,根据牛顿第三定律两光束对小球的作用力沿y轴正方向;所以两光束对小球作用力的合力方向必沿图14所示的左上方向.
点评 光束与微小实物粒子产生经典相互作用时,合理使用动力学规律进行分析是关键.
总结1)几何光学的命题方向与特点:
光的折射定律、折射率、全反射现象的考查常以计算题形式出现,是命题热点、常考点,且通常与几何作图、三角函数等知识有机结合,涉及的模型常有平行玻璃砖、三棱镜、圆柱体(球)形玻璃体及透明液体等.
2)处理几何光学问题的技巧:
b)折射率不仅与介质有关,还与光的频率有关,同种介质中频率越大的色光的折射率也将越大,光线偏折得越厉害,光的传播速度越小.
c)发生全反射的条件:① 光线从光密介质射向光疏介质; ② 入射角大于或等于临界角.
d)全反射的能量分配关系:折射角随着入射角的增大而增大,折射角增大的同时,折射光的强度减弱,即折射光的能量减小,亮度减弱,而反射光的强度增强,能量增大,亮度增加.
e)临界角:① 临界角的定义:光线从介质射向真空(空气)(即从光密介质射入光疏介质)时折射角等于90°时的入射角;

f)作出必要的辅助线,运用好几何关系及三角函数关系.

