用图象处理实验数据中的“化曲为直”方法
矫岩松
用图象处理实验数据往往能够直观地反映出物理量之间的关系.从实验测得的数据点出发,我们经常希望能找到一个函数来反映物理量之间的关系.实际中可能遇到的问题是:如果直接看两个物理量之间的关系,这个函数可能比较复杂,图象往往是一条曲线.在没有计算机辅助的情况下,曲线的参数就不好确定.这种情况下,如果事先对物理量进行适当的处理,再画出图象,数据点就有可能大致分布在一条直线附近,对应的函数关系就简化为一次函数,即线性关系.这样一来,用直尺就可以近似画出我们要寻找的函数关系了.求出这条直线的斜率和截距,我们就可以知道最初两个物理量之间的关系.这样处理数据的方法叫作“化曲为直”.
下面,我们先以“探究加速度与力、质量的关系”实验为例,来介绍这种方法的具体应用.然后,再讨论其他一些可以利用“化曲为直”方法的情况.
1 探究加速度与力、质量的关系
我们选取如图1所示的装置.假定已经补偿好各种阻力.设小车质量为M,槽码质量为m,重力加速度为g.我们要研究的是小车沿斜面下滑时的加速度a与小车所受的拉力F、小车质量M之间的关系.

图1
1.1 满足质量条件m≪M时
在满足质量条件m≪M的前提下,小车所受的拉力F可认为与槽码所受的重力mg相等.
我们以a为纵坐标、F为横坐标建立直角坐标系探究a与F的关系.根据各组实验数据在坐标纸上描点,作出a-F图象.如果描出的点在一条过原点的直线附近,说明a与F成正比.如果不是这样,则需进一步分析.

1.2 不满足质量条件m≪M时



①
即a与F成正比、与M成反比.但是,当m足够大,或者M不是很大时,分母的m就不能忽略了.这时候,加速度a与F和M的关系只能通过下式计算,不能加以简化.

②
此时,a与F或者M就不是简单的正比或者反比关系了.


图2


图3


③

图4

图5

下面我们通过几个例题来说明“化曲为直”方法在解题中的应用.


图6



值得注意的是,对于同一个实验,“化曲为直”的方法有时不是唯一的.本题答案为C.


图7






图8



2 “化曲为直”的其他应用
2.1 研究匀变速直线运动


图9


2.2 用单摆测量重力加速度的大小

图10


我们依然可以通过T2-l图象的斜率来求g.只不过这时图象多了截距,而截距反映了不知道的那部分摆长d.

2.3 验证机械能守恒定律


图11
实验中,先接通电源,再释放重物,得到图12所示的一条纸带.在纸带上选取三个连续打出的点A、B、C,测得它们到起始点O的距离分别为hA、hB、hC.某同学想用下述方法研究机械能是否守恒.在纸带上选取多个计数点,测量它们到起始点O的距离h,计算对应计数点的重物速度v,描绘图象,并做如下判断:若图象是一条过原点的直线,则重物下落过程中机械能守恒,请你分析论证该同学的判断依据是否正确.

图12



2.4 测量电源的电动势和内阻

(1) 请根据测定电动势E和内电阻r的要求,设计图13中器件的连接方式,画线把它们连接起来.

图13 图14


图15
(3) 在图15上把描绘出的坐标点连成图线.
(4) 根据图15描绘出的图线可得出这个电池的电动势E=________V,内电阻r=________Ω.

U=E-rI.
①
可见图象的斜率为内阻r的相反数,截距为电动势E.
如果有电流表和电阻箱而没有电压表,那么我们可以测出对应外电路电阻为R时,流过电源的电流I.可是I和R的关系并不是一次函数.由闭合电路欧姆定律可得

②
③
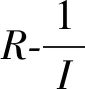
如果有电压表和电阻箱而没有电流表,那么类似地,我们可以测出对应外电路电阻为R时,电源两端的电压U.但是,U和R的关系也不是一条直线.因为将U=IR代入式②并整理,可得

④
但是,如果我们对式④两边取倒数,再整理一下,可以得到

⑤
答案(1)见图16.
(2)见图17.
(3)见图17.
(4)1.5(1.46~1.54); 0.3(0.25~0.35).

图16 图17
2.5 测定玻璃的折射率


图18
3 总结
“化曲为直”是高中阶段处理实验数据的一种常用方法.通过对实验数据的预先处理,复杂的函数关系可以简化为一次函数,使得曲线拟合变得简单易行.这既可以帮助我们找到物理量之间的关系,又可以简化一些物理量的测量.但是我们知道,更加严密的做法是通过适当的算法(如最小二乘法)计算出最合适的拟合直线(或曲线).如果有计算机辅助,那这样的工作也很容易实现.例如在Excel中,我们就可以通过选择多项式拟合,直接得到a与M成反比(即幂近似为-1)的关系.但是,“化曲为直”作为一种简化问题的思想方法,能把曲线(非线性)化为直线(线性),仍然值得我们学习.

