数学问题2155的新解与推广
郑娇凤 祝敏君 陈清华
《数学通报》2013年第12期中的2155号数学问题是一道经典的问题,本文在给出问题2155新解的基础上,得到以下三个结论. 1)发现该问题所得到的结论∠EAF=135°是EF=BE+DF的充要条件;2)问题2155对一般三角形仍然成立;3)问题2155可以推广到三维空间的三棱锥情形. 先回顾2155问题.
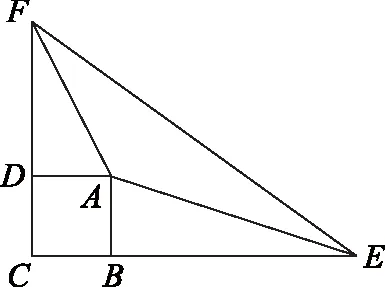
图1
如图1所示,在正方形ABCD中,E,F分别是CB,CD的延长线上的点,已知EF=BE+DF,求∠EAF的度数.
王远征老师给出了三角公式解法,吕爱生老师提供了几何解法,本文从向量视角给出新的解法,并对其结论进行相应的推广.
1 问题2155的新解

图2


①

ab-1=a+b.
②
2 ∠EAF=135°是EF=BE+DF的充要条件
根据本题的题设条件,我们发现:所求结果∠EAF=135°不仅是EF=BE+DF的必要条件,而且还是充分条件,即有
定理1如图1所示,在正方形ABCD中,E,F分别是CB,CD的延长线上的点,则EF=BE+DF的充要条件是∠EAF=135°.
证明必要性证明同上,下证充分性.
以C为原点,CE为x轴,CF为y轴建立直角坐标系(如图2),记AD=1,DF=a,BE=b,则

因为∠EAF=135°,所以
整理得
(a+b)2=(ab-1)2.

图3

a+b=ab-1.
①

②
3 问题2155在平面上的推广
定理1说明了直角三角形中边与角的一种关系,在一般三角形中是否也有这种边与角的关系呢?易知在满足条件EF=BE+DF或∠EAF=135°时,点A是△CEF的内切圆圆心,因此可以将定理1推广到一般三角形中.

图4




①

故

②

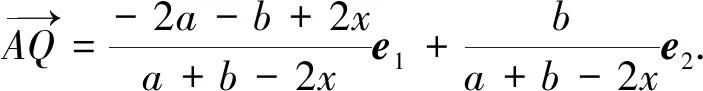
③
由式①②③有



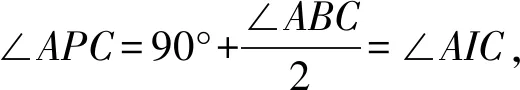

图5
因此P是△ABC内切圆的圆心,过点P向△ABC三边作垂线,垂足分别为E,F,H(如图5所示),则HA=EA,HC=FC,故
AC=HA+HC=EA+FC.
4 问题2155在空间上的推广
进一步考虑将定理从二维平面推广到三维空间.先回顾二面角平分面的一个性质.
引理四面体二面角平分面上任意一点到形成这个二面角的两个面的距离相等.
定理3如图6,在三棱锥A-BCD中,P是侧二面角平分面交线上一点,过P点分别作三棱锥的面ABC、面ACD、面ABD、面BCD的垂线,垂足分别为E,F,G,H,则S△EBC+S△FCD+S△GDB=S△BCD的充要条件是P为内切球的球心.

图6 图7
证明过点P,E,H的平面与BC交于Q(如图7).因为PE⊥平面ABC,所以PE⊥EQ,PE⊥BC;同理可证,PH⊥HQ,PH⊥BC;所以BC⊥平面PEH,于是EQ⊥BC,HQ⊥BC,即EQ,HQ分别是△EBC和△HBC边BC上的高.
充分性证明:因为P是内切球的球心,所以PE=PH,故△PEQ≌△PHQ(HL),从而有EQ=HQ,因此S△EBC=S△HBC.同理可证
S△FCD=S△HCD,S△GDB=S△HDB.
故S△EBC+S△FCD+S△GDB=S△HBC+S△HCD+S△HDB=S△BCD.
必要性证明:过点P,F,H的平面与CD交于S,过点P,G,H的平面与DB交于T.
因为PE2+EQ2=PH2+HQ2,所以PH2=PE2+EQ2-HQ2.同理有
PH2=PF2+FS2-HS2,
PH2=PG2+GT2-HT2.
因为P是侧二面角平分面交线上一点,所以PE=PF=PG,所以
EQ2-HQ2=FS2-HS2=GT2-HT2.
因此,(EQ-HQ),(FS-HS),(GT-HT)符号相同.
又因为S△EBC+S△FCD+S△GDB=S△BCD,所以
EQ·BC+FS·CD+GT·DB=
HQ·BC+HS·CD+HT·DB,
因此(EQ-HQ)=0,(FS-HS)=0,(GT-HT)=0,则PH2=PE2=PF2=PG2,所以P为内切球的球心.

图8

证明如图9,过P作PE⊥QM,PH⊥QN,因为BC⊥平面MQN,所以∠MQN=α,BC⊥PE.因为QM和BC相交,故PE⊥平面ABC,同理可证PH⊥平面BCD.

图9
因为P是三棱锥A-BCD内切球的球心,所以PE,PH都是内切球半径.以P为圆心PE为半径画圆,即球P与圆P半径相等,则MN与圆P必然相离,下面说明MN与圆P不可能相交或相切.
因为MN在平面ABD上,而平面ABD与球P至多只有一个交点,故MN与圆P也至多只有一个交点,即MN与圆P不可能相交.
若MN与圆P相切,切点记为G,则PG⊥平面ABD,故有PG⊥AB.又因为PE⊥AB,所以AB⊥平面MQN.已知BC⊥平面MQN,因此AB∥BC,矛盾,因此MN与圆P不可能相切.

顺便指出,三棱锥是正四面体时,MN与AD重合,上述结论仍然成立.对于其他二面角也有对应的结论,这里就不再赘述.

