高考复数问题的命题视角
刘勇华
复数在历年各省市高考试卷及全国卷中均以选择或填空题的形式出现,题目难度不大,考查内容主要涉及复数的有关概念、复数的运算、复数的几何意义、复数方程及复数的应用等.本文进行举例说明.
1 考查基本概念
复数的概念主要包括:复数单位i的性质,复数的实部和虚部、共轭复数、复数的模等.准确理解这些概念是求解问题的关键.

A. 充分不必要条件
B. 必要不充分条件
C. 充分必要条件
D. 既不充分也不必要条件




由复数单位的定义i2=-1,i4=1,所以i2 020=1,所以i+i2+i3+…+i2 020=0.







2 考查基本运算
复数的基本运算包括:加、减、乘、除、相等,求解中要准确理解、记忆相应的运算法则.如,复数的加、减法则,实部与实部相加减、虚部与虚部相加减;乘法法则,按分配律展开求解.除法法则,分母实数化.复数相等,实部与实部相等、虚部与虚部相等.







3 考查复数的几何意义
复数和复平面内的点具有一一对应关系,判断复数在复平面内对应的点所在的象限是高考常考题型.

A. 第Ⅰ象限 B. 第Ⅱ象限
C. 第Ⅲ象限 D. 第Ⅳ象限



A. (x+1)2+y2=1
B. (x-1)2+y2=1
C.x2+(y-1)2=1
D.x2+(y+1)2=1


4 考查复数方程的根
对于一元二次方程ax2+bx+c=0 (a≠0),若Δ=b2-4ac<0,则方程在实数范围内没有根,但方程在复数范围内存在虚根.对于求高次方程的虚根,可通过因式分解、转化等手段,将其化为低次方程求解.

A.p=-4,q=5 B.p=-4,q=3
C.p=4,q=5 D.p=4,q=3

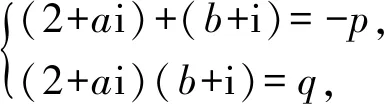
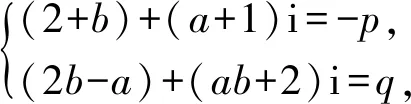
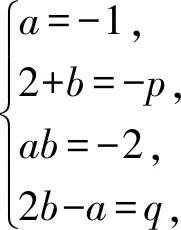



(x2+ax+1)(x2+bx+1),
即
x4+x3+x2+x+1=
x4+(a+b)x3+(ab+2)x2+(a+b)x+1.
由对应项的系数相等,得
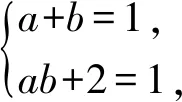
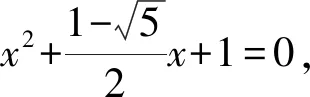
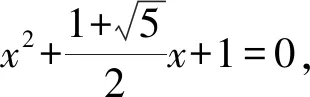

5 考查复数的应用
在某些问题的求解中,复数可以作为一种解题工具,即通过构造复数来解决问题.

证明令z1=x+yi,z2=a+bi,则z1+z2=(x+a)+(y+b)i,由复数的性质,可知|z1|+|z2|≥|z1+z2|,所以


