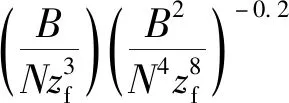静态温度分层水体中点源羽流云团垂向运动规律

陈 铂,彭梦辉,王 华

(1.长沙理工大学水利工程学院,湖南 长沙 410004; 2.水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410004)

经济高速发展使得我国环境污染形势严峻,而水污染事件已成为我国主要的突发性环境污染事件[1-8]。我国可建设的大型水电站共有1 360多座,其中很多都是高坝深库。大型深水库在蓄水后往往出现水体温度分层,使水库有着与河流不同的水温分层结构[9-11]。水库建成运行后,为处理类似新安江水库苯酚泄漏、墨西哥湾漏油事件等突发污染事件造成的环境问题,需要准确掌握温度分层水体中污染物运动规律,对污染情况进行预测和预警,为控制污染物扩散提供事故处理决策支持。

很多突发环境事件中,污染物泄漏是以瞬时点源羽流(thermal)的形式扩散。Scorer[12]研究了静态均质水体中的点源羽流云团运动规律,认为云团的运动会在一个顶角约为30°的圆锥体范围内;马福喜等[13]通过试验观测与大涡模拟也得到了相近的结果。Tarshish等[14]采用直接模拟方法研究了紊动热气团(turbulent thermals)运动规律,发现气团上升时均为椭球体,而气团加速上升时所受的浮力与椭球的高宽比相关;林伟波[15]对密度分层流中的浮射流进行了试验,并对垂向密度呈线性变化的垂直浮力射流进行了数值模拟,得到射流的密度场、射流轨迹、稀释度和射流宽度等的分布规律;黄海宁等[16]为研究碱渣倾倒入海洋后引起的污染情况,在静态温度分层水体中进行了碱渣云团和泥浆云团沉降试验,认为密度跃层对云团有阻碍作用，当分层强度大时,云团会停滞在密度跃层处振荡;分层强度弱时,云团会穿过跃层,但部分云团内的细颗粒仍会滞留在跃层。

点源羽流云团在温度分层水体中的沉降主要受浮力影响,水温结构不同时,浮力变化有很大差异,对云团垂向运动规律影响很大。本文通过物理试验,对静态温度分层水体中点源羽流云团垂向运动规律进行研究,为水库和湖泊中污染物扩散预测提供依据。

1 试验装置与试验方法

试验用水箱如图1所示,水箱中间位置布置有挡板,挡板下方先注入冷水,挡板闭合后在其上方注入热水,待水体平静后(约5 min)缓慢打开,形成温度分层水体。使用电热耦合温度计测量水箱中间垂线上温度随时间变化情况,结果如图2所示,可以看出不同温差的分层水体,在50 min内仍旧保持稳定的分层结构。污染物垂向扩散试验通常不到1 min,故在试验中忽略热量损失。所有试验中水箱中部温度梯度最大可以达到0.5℃/mm。

图1 试验水箱示意图(单位:mm)

图2 分层水体温度场

试验使用氯化钠和少量染色剂作为模拟污染物的溶质,与水混合形成模拟污染物溶液,模拟污染物室温下初始密度为1.028～1.126 g/cm3。试验中假定污染物云团的平均密度为云团内环境水体与污染物溶质的质量和云团体积的比值。使用3种方式在水体表面投放模拟污染物:①试验组R1使用一无底圆筒(图3(a)),内部填充纱网,试验时将圆筒大部置于水面以下,倒入5 mL污染物后提起,形成污染物云团;②试验组R2使用一硅胶软管(图3(b)),一端储存污染物(0.4 mL)，另一端密封,试验时将有污染物一端置于水面以上5 cm,打开另一端释放污染物,形成点源羽流云团;③试验组R3释放方法与R2相同(图3(c)),但其释放口略低于水面,释放污染物0.25 mL。由于投放污染物体积远小于环境水体,故认为污染物投放后立即与上层水体混掺,形成的云团内部温度与上层水体相同。

图3 污染物表层投放方式

采用摄像机拍摄羽流云团垂向运动过程,对试验图像进行分析并得到所需的各项参数。羽流云团沉降时其形状近似于椭球(图4),与Tarshish等[14]数值模拟结果相同,可认为云团是水平向两轴长度均为w、垂向高度为h的椭球。根据Beer-Lambert定律,将云团图像与原有背景之间的亮度差与污染物质量相关联,定性分析污染物浓度分布[17]。

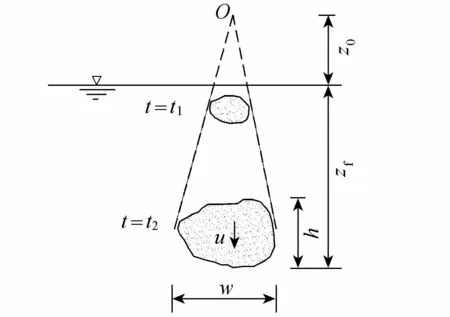
图4 羽流云团垂向运动示意图

将试验照片(图5)与原背景图片逐像素比较,得到由染色剂引起的亮度变化,使用云团内最大亮度变化值的50%作为阈值消去噪点(孤立的亮度变化像素点),再将最大亮度变化值的20%作为阈值勾勒出云团的边界。每一帧图片处理完后,将各像素点位置浓度分别在垂向和水平向叠加(图6),并按照时间顺序排列得到历时变化过程,如图7所示。根据边界位置计算云团宽度w和高度h,由浓度分布确定云团重心位置,并根据重心位置变化计算云团垂向沉速u。

图5 原始试验照片

图6 单帧图片垂向浓度分布和水平浓度分布叠加示意图

图7 污染物云团浓度分布叠加历时变化

2 试验结果与分析

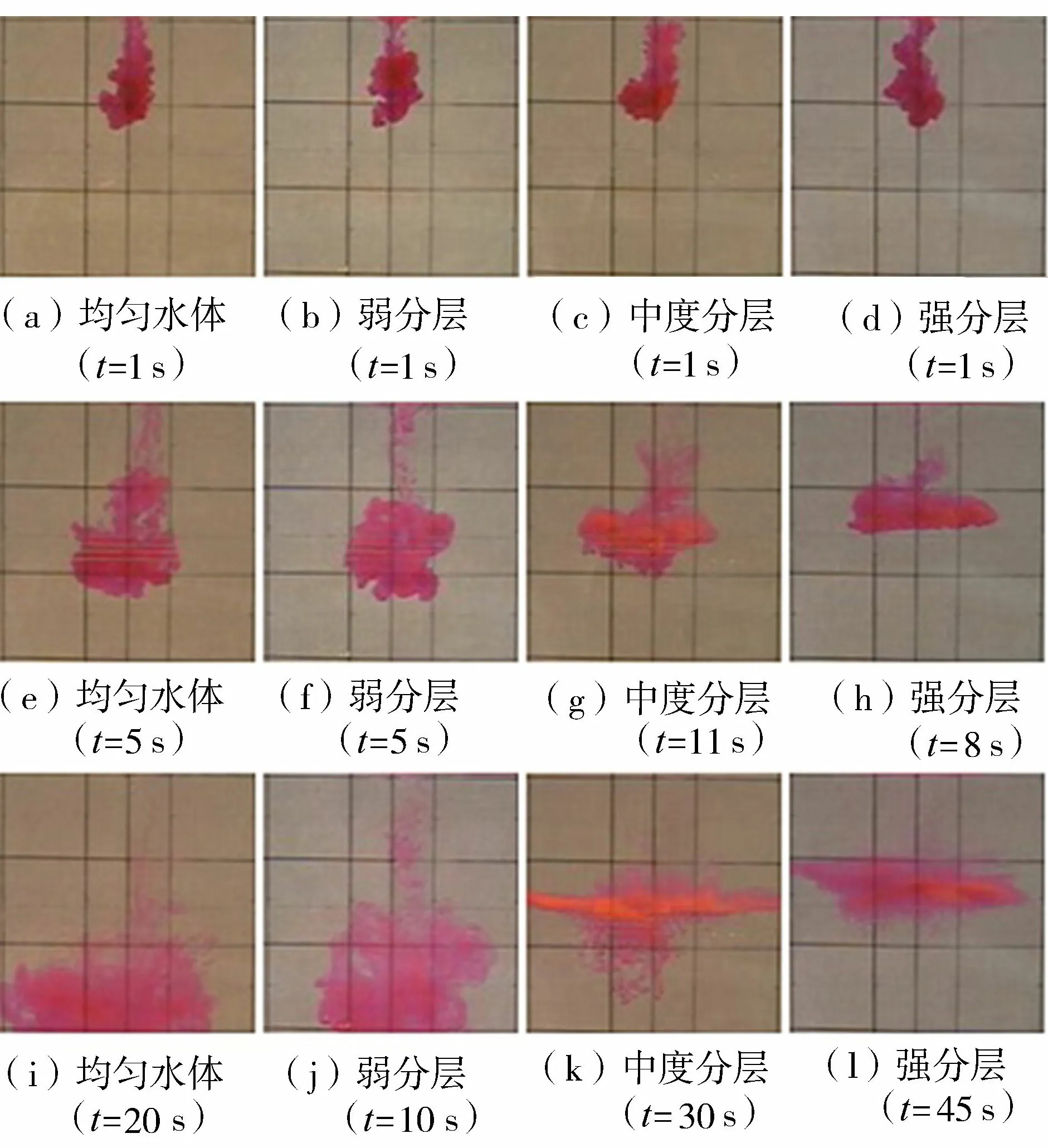
图8 羽流云团试验照片

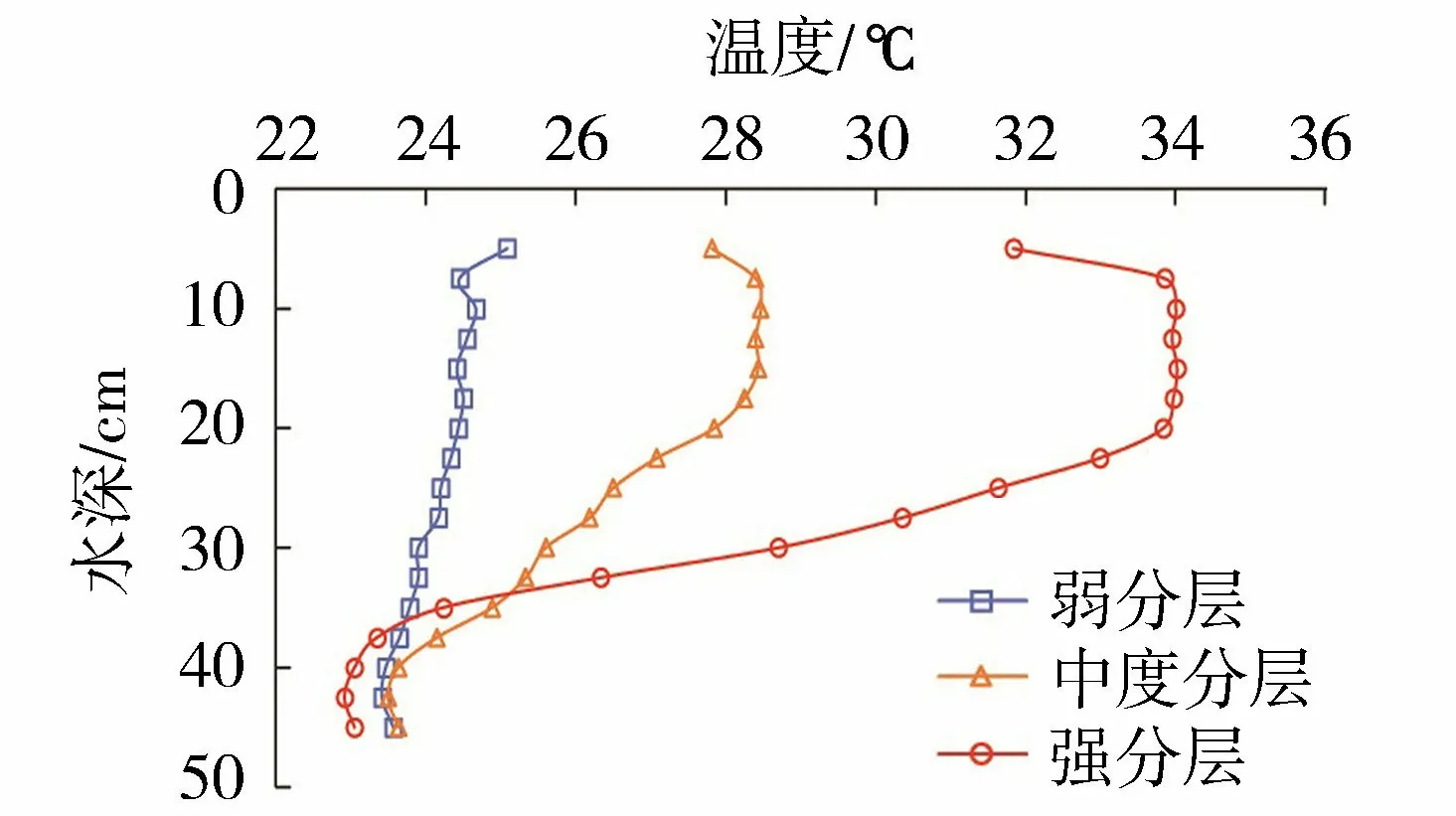
图9 试验环境水体温度场

图8为不同分层程度典型试验照片,不同水温结构的分层水体中,羽流云团的运动规律有着显著差异。当上下层水温差异较小时,温度梯度引起的浮力作用较弱,挡板开合产生的扰动会在垂向传播,最终形成近乎线性分层的水温结构(图9中弱分层)。此时,羽流云团的运动(图8(b)(f)(j))与均匀水体中的羽流云团(图8(a)(e)(i))相近,但垂向速度要小于不分层情况;同时由于线性分层水体内的斜压作用,横向扩散也受到限制。如果增大上下层水体温差,此时水箱内可以分为3层:上下层不同温度的均匀水体和中间温度线性分布的温跃层,如图9中的中度分层。此时的羽流云团在温跃层会受到明显的浮力顶托。由于云团内部浓度分布不均匀,浓度小的部分(密度小于下层水体)停滞在温跃层后会沿横向继续扩散,浓度大的部分(密度大于下层水体)会因Rayleigh-Taylor不稳定,产生尺寸较大的指状液滴,侵入下层水体,如图8(c)(g)(k)所示。上下层水体温差很大时,温跃层厚度会变得很小,此时可认为温度场为阶梯形分布,如图9中的强分层。由于较强的浮力作用,羽流云团会被阻滞在温跃层,由于温度梯度(上热下冷)和浓度梯度(上层水含溶质,下层为清水)的共同作用产生双扩散对流(double-diffusion convection)[18],云团下部会出现大量细小的指状对流液滴,如图8(d)(h)(l)所示。Chen等[19]测量了上述指状侵入液滴的尺寸与侵入量(中度分层试验与强分层试验),认为指状侵入液滴的量约为总污染物量的5%～20%,且其宽度大于双扩散盐指(salt-finger)宽度。显然其测量的指状液滴既有因双扩散对流产生的液滴,也包含了中度分层时Rayleigh-Taylor不稳定产生的液滴。

羽流云团垂向运动主要受浮力影响,其值为

(1)

u=f(B,N,zf)

(2)

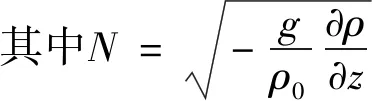
使用量纲分析可以得到分层水体中羽流云团的垂向沉速为

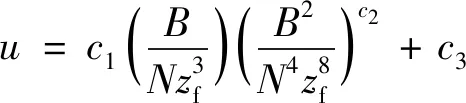
(3)

式中:c1、c2、c3均为系数。对于均匀水体,羽流云团的垂向沉速为

(4)

式中:c4、c5为系数。根据试验采集数据,采用文献[20]中的方法计算每组试验中的系数,所得结果如图10和图11(图中白点为中位数,黑色粗条为上、下四分位点,外部为对称的概率密度曲线)所示,系数c1、c2、c3、c4、c5中位数分别为0.44、-0.2、8.18、1.65和-3.46。

试验使用了3种不同的污染物投放方式,且污染物投放量也不相同,同时羽流云团在不同环境水体中的运动规律有很大差异(图8),为了解不同情况时羽流云团的垂向运动规律,需要分别分析沉速公式中的系数。由图10(a)和图11(a)可以看出,投放方式R2试验得到的系数c1和c4与其他投放方式有明显差异,显示R2试验中采取水面以上5 cm投放污染物,污染液滴下落产生的较大初始动量对云团垂向运动有影响。而分层水体羽流云团沉速公式(式(3))中的幂指数c2在不同投放方式和水温结构中变化不大,且都集中在-0.2附近;相反c3和c5的值虽然受投放方式或水温分层影响不大,但数值较为离散。式(3)中的c1和c3以及式(4)中的c4和c5,与具体试验时的初始动量、虚源点O位置(见图4,综合反映投放位置和投放量)和试验误差相关,不同情况会有一定差异;式(3)中的幂指数c2反映了各物理量之间的关系,受初始状态影响较小。

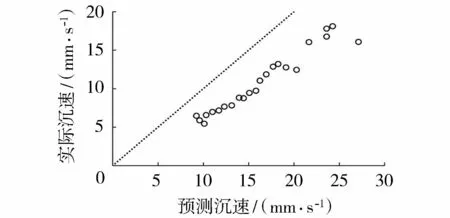
图12 典型试验云团垂向沉速关系

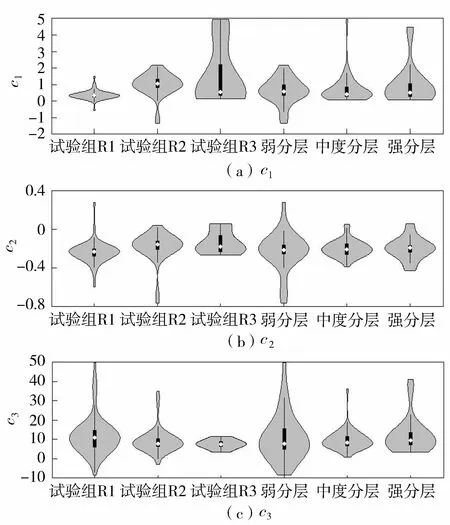
图10 分层水体沉速公式系数小提琴图

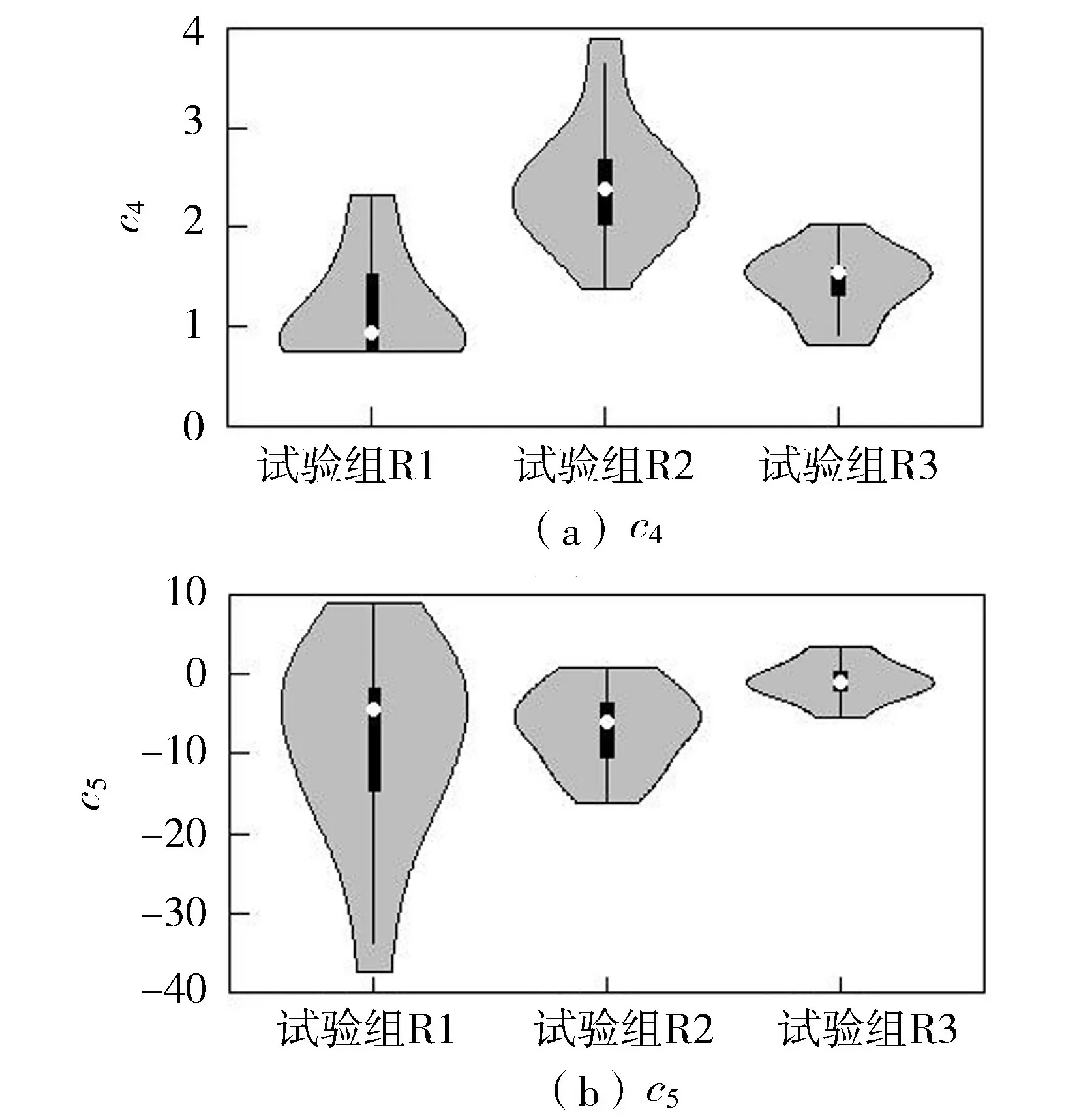
图11 均匀水体沉速公式系数小提琴图

将分析得到的c1、c2和c3的中位数代入式(3),即可以预测分层水体中污染物云团垂向运动。图12为弱分层、投放方式为R1的云团垂向沉速预测值和实际值,可见预测沉速与实际沉速趋势相同,但由于不同条件下,污染物初始速度、污染物总量和污染物与环境水体密度差都不相同,导致了预测沉速与实际沉速之间的差异,这也是今后需要继续研究的方向。

3 结 论

a. 不同水温结构中羽流云团的垂向运动有很大差异,在线性分层水体中云团下沉过程中横向扩散受到一定限制。

b. 在有温跃层的水体中,云团会在温跃层位置停滞,由于云团与环境水体密度之间的差异,可能出现Rayleigh-Taylor不稳定或双扩散,并出现指状侵入,且其尺寸较盐指要大。