无线网状网中多并发流路由结合调度的组合方案

黄启嵩, 曹霑懋, 单志龙

(华南师范大学计算机学院， 广州 510631)

无线网状网(Wireless Mesh Networks,WMNs) 作为无线宽带服务的技术，旨在提供无处不在的信息服务[1]. 由于移动终端爆发式增长，多用户同时发出传输请求是常态[2]. 如何有效利用资源以减少干扰成为提高系统传输性能的关键问题. 多并发流的问题是由多对传输请求这个共有现象抽象出的多路不同的源节点到目标节点对之间的数据流并发的问题,要解决此问题，需为每路数据流分配链路以传输数据. 若多路数据流之间的路径没有合理地协调调度，数据流所选取的路径将可能交错在一起，产生节点负载不均衡现象[3]，从而导致请求的传输任务不能及时完成,以至于影响网络性能，且造成无线网络资源的浪费.

多并发流的问题，单独考虑路由、信道分配或调度都被证明是NP-Complete的[4]. 对此问题，学者们从不同角度提出解决方案. 如：提出一种分布式联合候选节点选择和速率分配的多流机会路由算法，通过速率分配确定并发流下机会路由的候选节点[5]；提出一种宽松的联合协作路由选择和信道分配算法，解决多数据流下协作路由和信道分配[6]；提出一种分布式算法用以最小化信道的最大拥塞，解决了基于MIMO的多并发流的路由问题[7]；提出一种干扰感知的路由度量，该路由度量考虑了流内和流间干扰以及链路速率，在多并发流的网络下尽可能地选择能够并发且互不干扰的路径[8]；进一步提出了一种基于博弈论的干扰感知信道分配算法，公平地将网络非重叠信道分配给接口，有利于增加多并发流条件下并发传输的连接数量[9]；通过广义Benders分解方法解决联合信道分配、链路调度、路由和速率控制的问题，从而获得多数据流下信道分配的最优方案[4]；提出一种负载均衡链路层协议，该协议按干扰的大小进行信道分配并基于霍夫曼树按链路的负载进行调度，实现了多数据流下节点接口间的负载平衡，但未能实现多数据流下节点间的负载平衡[10]；提出一种跨层联合信道分配和路由算法，该算法在信道分配阶段贪婪地选择干扰最小的信道，并在路由阶段提出一种结合了路径剩余容量和预期传输时间的新路由参数[11]. 从资源利用角度，同时考虑多并发流的路由、信道分配和调度问题是一种有益的探索[12]. 然而，现有的解决方案大多针对多路数据流并发问题在路由、信道分配和调度等方面中的1个或者2个方面，并未能将这几个方面有效结合起来.

基于这些研究的启发，本文将路由、信道分配和调度结合起来，提出一种依托信道分层方法的组合式路由结合调度的方案，以期更有效地利用资源和提升传输性能.

1 模型及算法

1.1 图模型

为了减少信道分配的复杂度，引入笛卡尔乘积(Cartesian Product of Graph,CPG)模型[13]，方便多并发流条件下路径选择判据的讨论. 多并发流下的无线网状网结构可用Γ={G,I,Ω,ξ,{(si,di)}}来表示，其中：

(1)G=(V,E)为无向网状图，|V|代表节点数量，|E|代表边的数量；

(2)I为G上节点之间的无线干扰关系；

(3)Ω={c1,c2,…,cq}为G上可用正交信道的集合，q为网络中正交信道的数量；

(4)ξ为节点接口数量；

(5){(si,di)}(i=1,2,…,ρ)为多个源节点到目标节点对的集合；

(6)Λ={i}={(si,di),zi}为列表{(si,di)}相对应的传输请求队列，zi(zi>0)为数据的大小.

在无线网状网中，路由问题是为每一个传输请求确定一条从源节点到目标节点的路径. 路径可被视为一条包含了有限个首尾相接的连接构成，可以用一个顺序的节点序列表示. 信道分配是为所选择的路径上的每一条连接分配信道. 调度是将一个传输时隙分配给找到的路径上的每一条连接. 从源节点开始，数据包被逐跳传输到后继节点，直到传输到目标节点为止.

根据正交信道的数量q，CPG模型将网状网分为q个虚拟层，各层拓扑结构相同，所属正交信道不同. 此时，一个多信道多接口节点因其参与通信的信道层，其身份转化为信道差异的节点，本质上还是该节点自身. 为每一条连接寻找可用信道时，只需逐层检测当前网络层下的信道可用性. 若该连接在当前网络层下能满足同一信道中的连接可共存条件[14](2个不同的发射节点间的距离不小于2跳；2个不同的接收节点间的距离不小于1跳；发射节点与接收节点间的距离大于1跳)，则当前网络层所属的信道为该连接的可用信道.

1.2 路径选择判据

为解决路由问题，首先，需要根据当前网状网的拓扑以及可用资源找到几条可选路径；其次，基于路径选择判据，从可选路径中选择最合适的一条路径. 尽管以跳数作为路由度量的最短路径并不能获得较好的网络性能[15]，但在网络资源充足的情况下，最短路径由于其跳数小、占用资源少的特点仍为首选路径. 另外，寻找其他路径与最短路径进行比较，以找到最合适的路径.

在路径发现阶段，对给定节点对(si,di)，先采用BFS算法找到一条(si,di)的最短路径，确定其长度li，并将该最短路径放入路由表中. 然后采用回溯法搜索可用路径. 为了防止路径长度过长，占用过多网络资源，回溯法将路径长度的限制参数δi作为约束条件. 路径长度的限制参数δi的计算公式如下：

δi=li+α,

(1)

其中，α为常数参数，该参数值由实验者根据实验需要指定. 同时，为了避免无休止地搜索可用路径，当可用路径的数量为3时终止，并将所搜索到的可用路径放入路由表中.

经过路由发现，(si,di)的路由表中将有4条可用路径，包括最短路径以及3条由回溯法发现的可用路径. 在后续的路径选择阶段，将从(si,di)的路由表中选出最合适的一条路径. 为此，需要建立一个合适的路径选择判据. 本文将节点的可用接口数量和可用信道数量定义为节点可用资源. 其中，节点的可用接口指的是节点未被占用的接口，节点的可用信道指的是与当前已存在的信道分配不冲突的信道. 对于一条路径，其可用资源主要体现在路径上所有节点的可用资源. 一条路径的可用资源越多，路径上节点的可用资源越多，路径上节点被占用的资源也就越少，则路径上节点负载越轻. 因此，选用可用资源多的路径，能够有效地绕过节点过载的区域，智能地选择负载较轻的节点，实现节点负载均衡，从而避免资源竞争现象，有效地利用网络资源.

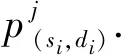
(2)

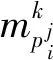
(3)

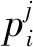
1.3 资源有效利用

同一时隙下，更多的激活连接可以传输更多的数据，实现网络的高性能传输. 为了有效利用网络资源，在每个正交信道下找到更多的激活连接，并将其组合到一起以形成更多的路径[14]. 这种通过恰当地组合正交信道上的多条无干扰连接而形成的路径，称之为可兼容路径. 可兼容路径上的每一条连接恰当地选择最合适的信道，以规避可能产生的无线干扰，使其不会与此前已有路径占有的信道分配产生冲突. 在整个网状网中，多条路径只有满足可兼容条件才能够并发传输.

找到可兼容路径最关键的一点是：路径上的节点有可用接口且所有跳的邻节点对有可用信道. 确定一个节点是否有可用接口并不难，困难的是确定邻节点对的可用信道. 对于路径上某跳的邻节点对，即发射节点和接收节点，其可用信道为发射节点和接收节点的可用信道集合的交集. 只有当发射节点和接收节点都工作在同一正交信道时，才能够建立连接，并进一步激活.

1.4 组合优化调度

要实现网络资源的最大化利用，需要在Γ中调度尽可能多的连接，也就是说最大化多并发流连接的数量[16]. 本节将结合路由、信道分配和调度，提出一种组合优化调度方案(Combinatorial Optimization Scheduling Scheme,COSS).

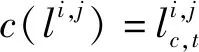
组合优化调度方案的具体流程见算法1.

算法1组合优化调度方案

输入：Γ,Λ.

forv=1 to |V| do

updatedv;

updatecv;

end for

fort=1 toTdo

fori=1 toρdo

forj=1 toLido

vsis the sender ofli,j;

vdis the receiver ofli,j;

if (cvs>0)∧(cvd>0)∧(cvs∩cvd≠∅) then

select one channelckfromcvs∩cvd;

else {at least one condition is not satisfied}

cancel the channel assignment forli,k,k=1 toj;

break;

end if

end for

ifj==Lithen

end if

end for

end for

该方案的具体步骤如下：

(1)在调度前，收集网络的全局信息，包括节点、传输请求和网络拓扑等. 基于全局信息，更新所有节点的状态，对所有传输请求作出合理的全局规划，也就是协调调度.

(2)在调度时，首先将T划分为多个时隙ti(ti=1,2,…,T). 在每个时隙下，逐一检查未加入的所有路径是否为当前时隙下的可兼容路径. 若符合可兼容路径条件，则将该路径分配合适的信道和当前时隙，并加入中. 反复检查，直到所有路径都加入到，算法结束.

(3)一条路径是否为可兼容路径，可根据该路径上的所有连接是否有可用资源来判定. 若路径上的所有连接都有可用资源，则该路径在当前时隙下为可兼容路径. 若路径上某一连接没有可用资源，则该路径在当前时隙下为不可兼容路径，该路径所分配的信道将被释放.

算法1将网络拓扑的更新周期T分为多个时隙，通过逐一遍历所有路径，为符合可兼容路径条件的每条路径上每一跳的邻节点对分配无干扰的信道及时隙，使之成为可兼容路径，并将路径加入到可同时调度的路径组中. 通过启发式的方法找到每个时隙下尽可能多的可兼容路径，实现所有可兼容路径组合优化调度，最大化同一时隙下可兼容路径的数量. 而同一时隙下更多的可兼容路径可传输更多数据，有效地提高了网络资源的利用.

2 仿真实验

本文将分别在不同网络资源配置、多种流量请求下进行仿真实验，根据网络最大吞吐量、平均端到端时延、传输时间3个性能参数评估本文的COSS算法性能. 更进一步，选用AODV路由协议[17]与COSS算法做对比实验.

2.1 仿真场景及评价指标

实验场景是在1 000 m*1 000 m的区域范围内随机生成64个节点，如图1所示. 在仿真参数设置上，每个节点的可用接口数目R{4,8,12,16,20}，网络的可用正交信道数量C{8,16,32,64,128}，数据包大小为1 MB，每个传输请求的数据包数量为250个，链路容量为200 MB/s，时隙为5 ms，时间周期为0.5 s.

在性能指标上，采用能够反映网状网性能的指标：网络最大吞吐量、平均端到端时延、传输时间. 这些指标定义如下：

(1)网络最大吞吐量：在某个单位时间内目标节点所接收的最大数据量.

(2)平均端到端时延：一个数据包从源节点传输至目标节点所需的时间.

(3)传输时间：所有传输请求从开始发送数据到全部数据被接收所需的时间.

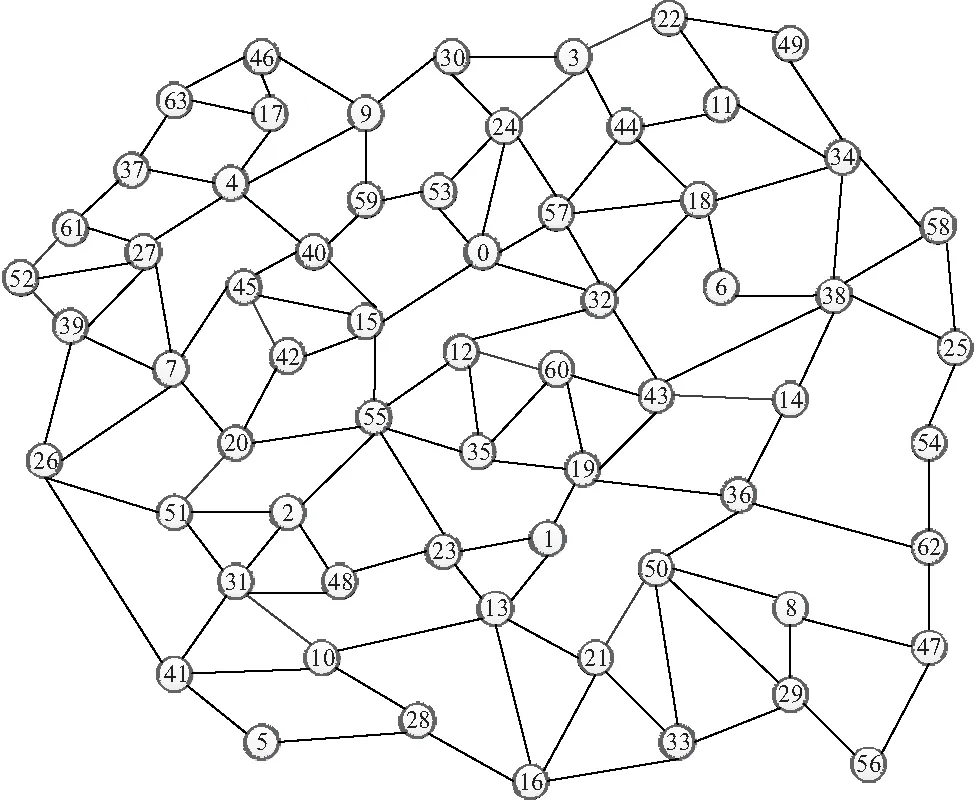
图1 64节点随机拓扑图Figure 1 The 64-node random topology

2.2 性能比较

2.2.1 不同网络资源配置下的性能 将传输请求节点对数量设置为80对，通过改变网络资源配置(节点接口数量和正交信道数量)，分析算法在不同网络资源配置下性能指标的变化情况.

由图2可知：(1)当C=8时，随着接口数量的增加，网络最大吞吐量并未有显著提升. 这表明了该例中限制网络最大吞吐量的主导因素是信道数量. (2)当C=16、C=32时，随着接口数量的增加，网络最大吞吐量快速提升，但明显因信道数呈现顶板效应. 这表明了接口数量较少时，限制网络最大吞吐量的主导因素为接口数量；而当接口数量足够多时，限制网络最大吞吐量的主导因素变为信道数量. (3)当C=64、C=128时，网络最大吞吐量的折线几乎重叠在一起，随着接口数量的增加而不断提升. 这表明了当R≤20、C=64/C=128时，信道数量已经足够多，网络最大吞吐量不再显著提升，此时限制网络最大吞吐量的主导因素是接口数量.

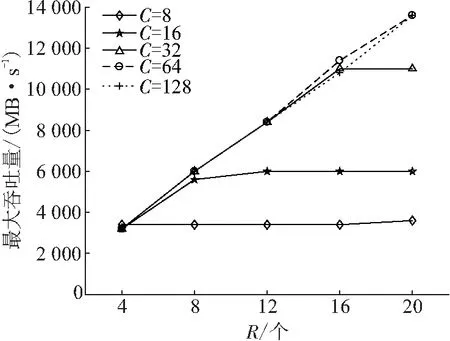
图2 不同接口数量、信道数量下的最大吞吐量变化Figure 2 The changes of maximum throughput with different numbers of radios and channels

由图3可知：随着网络资源配置的增加，网络平均端到端时延维持稳定且较小，网络资源配置的增加并不会对网络平均端到端时延产生影响. 这是因为经过组合优化调度，同一时隙下的可兼容路径间互不干扰，不会产生数据包重传、丢包和网络延迟高等情况，因而在不同的网络资源配置的条件下，网络平均端到端时延较为稳定且较小.

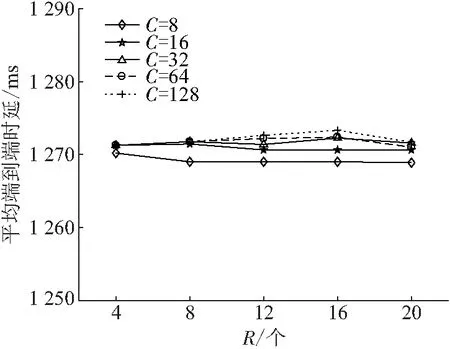
图3 不同接口数量、信道数量下的平均端到端时延变化Figure 3 The changes of average end-to-end delay with diffe-rent numbers of radios and channels

由图4可知：随着接口数量的增加，拥有更多信道数量的网络的传输时间减少得更快. 这是因为COSS算法能够有效地利用信道资源，最大化同一时隙下可兼容路径的数量. 但是，对于给定的信道数量，当接口数量超过某个阈值时，由于网络中可用信道数量的限制，同一时隙下可兼容路径的数量已达峰值，传输时间不再减少.

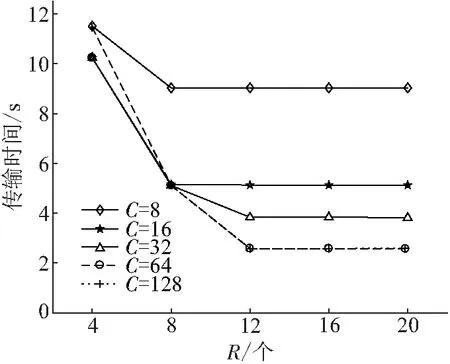
图4 不同接口数量、信道数量下的传输时间变化Figure 4 The changes of transmission time with different numbers of radios and channels

2.2.2 多种流量请求下的性能 网络资源配置分别设置为R=4∧C=8、R=12∧C=32、R=20∧C=128，通过改变节点对数量(从10对到160对)，分析算法在不同节点对数量下性能指标的变化.

由图5可知：随着节点对数量的增加，拥有更多网络资源配置的网络的最大吞吐量增加得更快. 这是因为网络资源配置的提升能有效地提高网络承载能力，使网络在同一时隙下的可兼容路径增多. 同时，网络的最大吞吐量最终都趋于一个稳定的值，这是因为节点对数量已经超过网络承载能力，网络同一时隙下可兼容路径的数量已达峰值，故而网络的最大吞吐量不再有显著的提升.

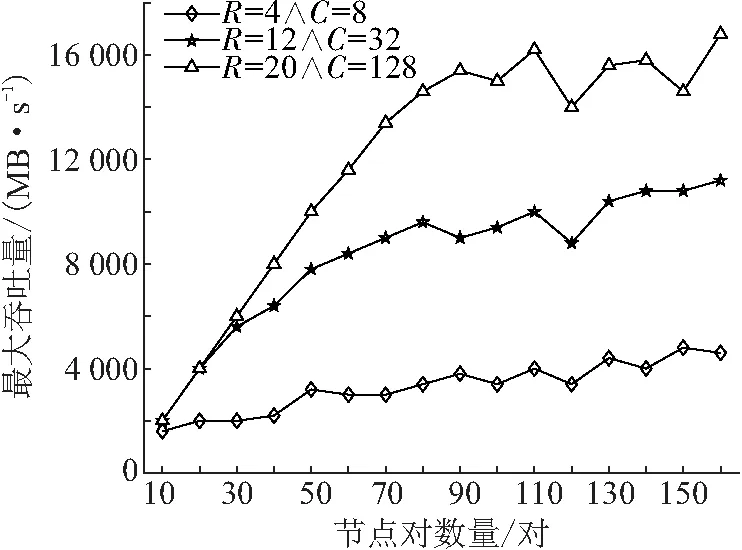
图5 不同节点对数量下最大吞吐量的变化Figure 5 The changes of maximum throughput with different numbers of pairs

由图6可知：随着节点对数量的增加，不同网络资源配置下的平均端到端时延依旧保持稳定. 这说明在多节点对数量下，COSS算法依旧能够合理调度每个节点对，使其能够在合适的时隙下无干扰地完成传输任务. 这也同样表明了COSS算法在高负载下能够保持高资源利用率，使数据的传输保持稳定.

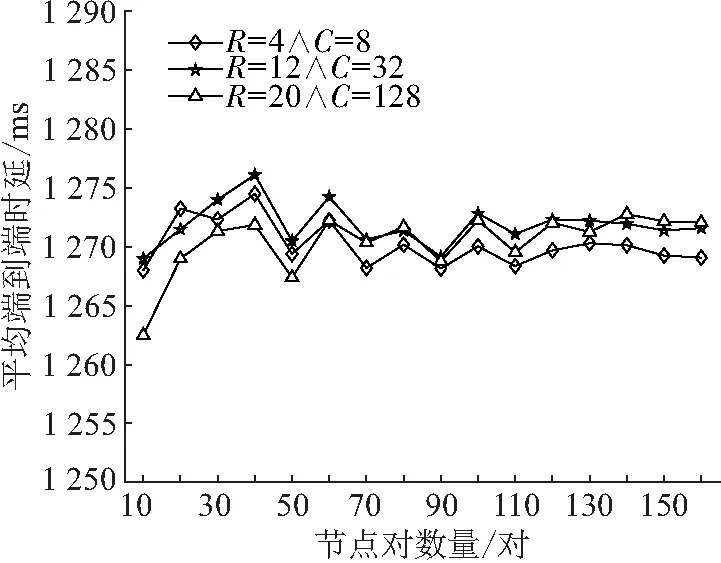
图6 不同节点对数量下平均端到端时延的变化Figure 6 The changes of average end-to-end delay with diffe-rent numbers of pairs

由图7可知：(1)当网络资源配置为R=4∧C=8时，随着节点对数量的增加，网络传输时间几乎呈线性增长. 这是因为受限于有限的网络资源配置，同一个时隙下激活的可兼容路径数量有限. 当节点对数量增加时，超过网络承载能力的这部分节点对将被分配到下个周期传输数据，从而使得传输时间增加. (2)当网络资源配置为R=12∧C=32时，传输时间呈阶梯状增加. 取其中一段阶梯(传输请求的节点对数量从10对到40对)为例：当节点对数量从10对增加到30对时，网络负载并未到达网络承载能力的瓶颈，无需增加时间周期便能完成传输任务；当节点对数量从30对增加到40对时，由于网络负载已经超过网络承载能力的瓶颈，超出网络承载能力的这部分节点对将被分配到下个周期传输数据，因而所需传输时间增加. (3)类似地，当网络资源配置为R=20∧C=128时，所需传输时间也呈阶梯状增加.

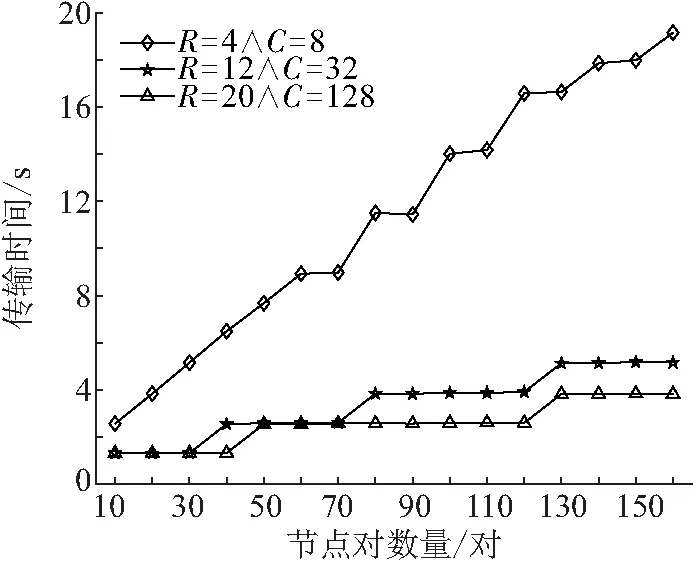
图7 不同节点对数量下传输时间的变化Figure 7 The changes of transmission time with different mumbers of pairs

2.2.3 对比实验 在对比试验中，本文选用了AODV路由协议作为对比算法. AODV路由协议是一种按需的路由协议，允许节点迅速获得到达目的地的路由，且并不需要维护超出自己辐射范围的路由.

网络资源配置分别设置为R=4∧C=8、R=12∧C=32、R=20∧C=128，通过改变节点对数量(从10对到160对)，比较COSS算法与AODV路由协议在不同节点对数量下平均吞吐量的变化.

由图8可知：在不同的网络资源配置下，COSS算法的平均吞吐量均优于AODV路由协议. 而且，随着网络资源配置的提升，COSS算法的性能优势愈加凸显. 这是因为AODV路由协议在路由阶段时选用跳数作为路径选择判据，并未能充分考虑网络资源；而COSS算法在路由阶段时选用了资源可获得度作为路径选择判据，能够智能选择当前网络资源下最大可用资源的路径，有效地减少了多对节点对路径之间的节点交叉重复度，实现了节点负载均衡，从而提升了网络性能.

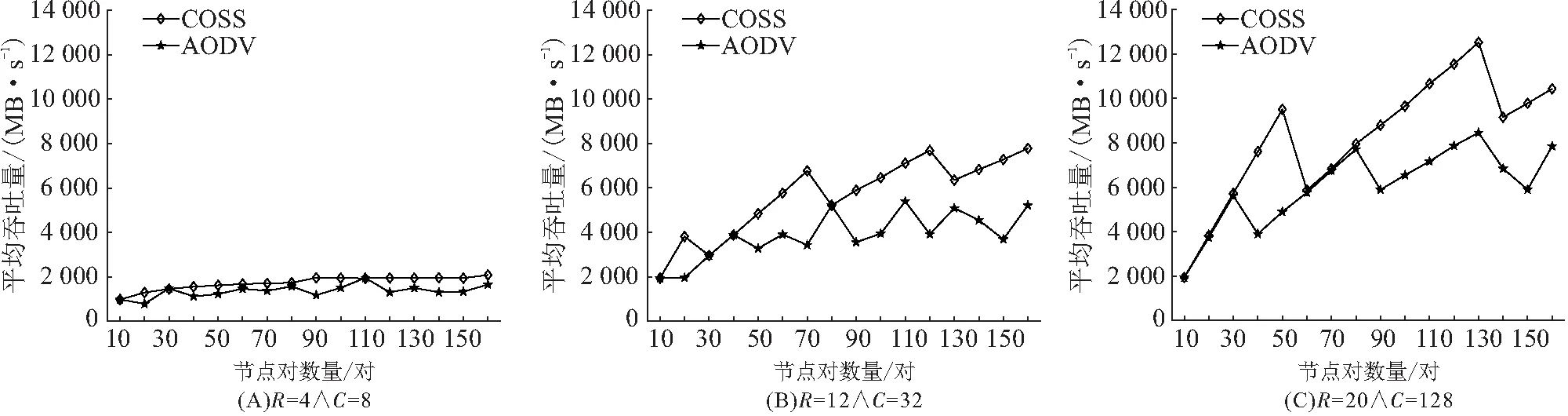
图8 2种算法的平均吞吐量比较Figure 8 The comparison of average throughput between two algorithms

3 结论

针对多并发流的问题，本文提出了一种结合路由、信道分配和调度的组合优化调度方案，旨在最大化网络资源的利用，减少多并发流下路径间的无线干扰. 该方案首先基于已经收集的全局信息，包括节点、传输请求和网络拓扑等，为多数据流协调建立资源可获得度最大的路径；然后，为这些路径协调分配无干扰的信道，使之成为可兼容路径；最后，组合优化调度所有可兼容路径，最大化同一时隙下可兼容路径的数量. 实验表明：该方案在不同网络资源配置、多种流量请求下均能取得较好的性能，并在吞吐量上优于AODV路由协议.