代数体函数的几个定理

谭 洋

(北京师范大学珠海分校应用数学学院, 珠海 519085)

代数体函数的唯一性是值分布论中的一个重要研究课题,已有一些研究成果[1-11]. 如，VALIRON[10]给出了著名的4v+1值定理;HE[11]得到了改进的4v+1值定理;何育赞[1]研究了涉及重值的代数体函数的唯一性;孙道椿和高宗升[7]定义了 代数体函数的运算并进一步研究了涉及重值的代数体函数的唯一性;姜云波和高宗升[3]研究了2个代数体函数记重数分担公共值的唯一性问题. 我们知道,Nevanlinna开创了亚纯函数值分布理论并得到亚纯函数五值定理[12]、四值定理[13]. 之后，很多学者对亚纯函数值分布进行了深入研究. 如强化了亚纯函数五值定理,得到亚纯函数五值强化定理[14].

在文献[13-14]的基础上,本文研究了代数体函数的唯一性问题和分担值较少时2个代数体函数的特征函数之间的关系,分别将亚纯函数五值强化定理和四值定理推广到代数体函数.

1 基本概念和相关性质

关于代数体函数的一些基本性质和结果可参阅文献[15-16]. 本文的符号除特别说明外均采用 Nevanlinna 理论的常用符号[14-16]. 本文中用表示复平面,用表示扩充复平面.

设Ak(z),Ak-1(z),…,A0(z)是定义在复平面上的一组没有公共零点的全纯函数,则方程

Φ(z,W)=Ak(z)Wk+Ak-1(z)Wk-1+…+A1(z)W+A0(z)=0

(1)

ψ(z,M)=Bs(z)Ms+Bs-1(z)Ms-1+…+B1(z)M+B0(z)=0.

设W(z)是由式(1)定义在复平面上的k值代数体函数. 称z0是W(z)的临界点,当且仅当Ak(z0)=0或者Φ(z0,W)与偏导数ΦW(z0,W)有公共根(即Φ(z0,W)有重根,z0为分支点). 所有临界点之集称为临界集,记为Sw,称其补集Tw=-Sw为正则集. 每一个临界点z0Sw是孤立点,在z0附近|(z-z0)kW(z)|有界,且是可去奇点或极点,因此,代数体函数W(z)在球面上是按球距连续的. 本文研究的函数一般只在正则集Tw中讨论,剩下的孤立临界点由连续性即可唯一确定.

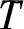
设W(z)是k值代数体函数,a(a,W)表示所有W(z)-a的零点集合(不计重数)，表示在|z|≤r内W(z)-a的所有零点数(不计重数，但包含有分支点的零点),表示在|z|≤r内W(z)-a和M(z)-a的所有公共零点数(不计重数). 相应的计数函数分别记为(r,1/(W-a))及0(r,a),称a是2个代数体函数W(z)和M(z)的IM公共值,若(a,M).

下面给出亚纯函数的五值强化定理和四值定理:

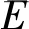
则f(z)≡g(z).

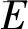
(ii)

(iii)对任意的a≠aj(j=1,2,3,4),有

引理1[15]设W(z)为方程(1)所定义的v值代数体函数,aj是q个不同复数(有穷或否),则

当W(z)为有穷级时,有

S(r,W)=O(logr) (r→);

当W(z)为无穷级时,有

S(r,W)=O(logrT(r,W)) (r→,rE),

可能除去一个线性测度有穷的r值集E.

引理2[15]设W(z)和M(z)为2个v值代数体函数,若W(z)≢M(z),则

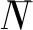
2 主要定理及证明

本文将定理A推广到代数体函数,得到:

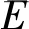
则W(z)≡M(z).

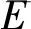
(2)

由式(2),有

再由引理2,有

(3)

再结合引理1可得

(4)

整理式(4),有

所以

这与题设条件矛盾,所以W(z)≡M(z). 证毕.

为研究分担值较少时,2个代数体函数的特征函数之间的关系,将定理B推广到代数体函数：

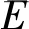
(ii)

(iii)对任意的a≠aj(j=1,2,…,4v),有

证明(i)由引理1,有

此外,由于

所以

T(r,W)≤(1+o(1))T(r,M),

T(r,M)≤(1+o(1))T(r,W).

从而得到(i)的结论.

(ii)由(i)可知

(1+o(1))v[T(r,W)+T(r,M)]=

(2v+o(1))T(r,W),

则

同理有

从而得到(ii)的结论.

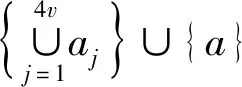
(2v+1)(1+o(1))T(r,W)≤

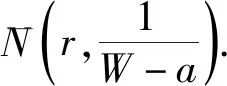
再由代数体函数第一基本定理有

从而有

同样可以得到

证毕.