硅波导纵向多模式分离与交叉的片上解决方案

朱 凝， 骆 晖， 张 凯， 刘 琼， 汪 洋

(华南师范大学半导体科学技术研究院∥广东省光电功能材料与器件工程技术研究中心，广州 510631)

随着社会对数据应用需求的急剧增长[1-2]，不同光通信技术相继被提出以应对在通信容量上的新挑战，例如空分复用(Space Division Multiplexing,SDM)、波分复用(Wavelength Division Multiplexing,WDM)、极分复用(Polari-zation Division Multiplexing,PDM)和模分复用(Mode-Division Multiplexing,MDM)等[3-6]. 在这些技术中，MDM技术允许每个波长下不同导模在多模光纤或波导内部可以传输不同的信号，光传输系统在单波长下的原始容量随导模数量的增大而等比例增加. 因此，理论上MDM技术可满足现代社会对信息容量不断增长的需求，这使其成为对当前WDM系统传输进行极限拓展的一个有利方式[7-8].

MDM技术在芯片上的数据通信中也颇受关注[9]，因为可以通过精心设计的光子集成回路(Photonic Integration Circuits,PIC)来传输和转换多模波导内不同的固有模式信号. 然而，在近年来关于多模片上器件的研究[10-11]中，几乎所有与MDM相关的研究都集中在横向多模上. 因此，研究适用于纵向多模集成光子器件具有重要的应用价值. 本文研究几种片上多模器件，这些器件继承了绝缘体上硅(Silicon-On-Insulator,SOI)平台的技术兼容性和成熟度，并可实现硅波导内部纵向多模的模式分离和交叉.

1 模式分离器件

1.1 横向、纵向多模波导

在横电(TE)偏振下，研究包覆于SiO2中的硅波导在横向和纵向上的基模、一阶模和二阶模，绘制出主要电场分量Ex的场振幅分布(图1). 横向多模波导(图1A)的宽度和高度分别为1 500、400 nm；而纵向多模波导(图1B)的宽度和高度分别为400、1 500 nm. 纵向多模波导通常具有比横向多模波导小得多的弯曲半径(20～30 μm)，这是由于弯曲区域中模场的横向畸变对纵向分布的模式正交性影响小，从而有效降低了模间串扰[12]. 此外，在未来应用中信息传输有可能需要使用二维多模波导结构(横向和纵向均为多模场分布)，以进一步提高最终传输速率.

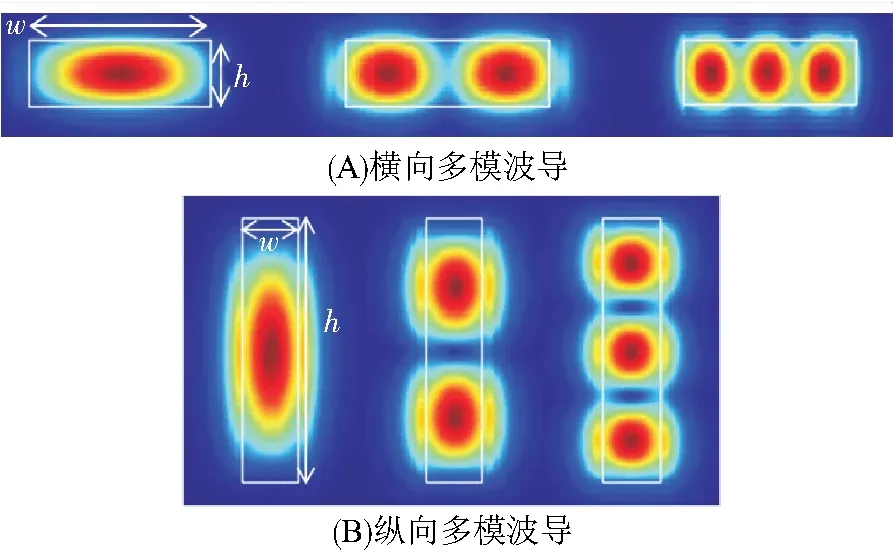
图1 在Si横向、纵向多模波导中前3个准TE模式在波长1 550 nm处的横向电场振幅分布
Figure 1 The electrical field amplitudes of the first three quasi-TE modes at the wavelength of 1 550 nm in the Si horizontal and vertical multi-mode waveguide
注：2个多模波导的尺寸均为400 nm×1 500 nm(波导放置方向不同)，其结构的轮廓用白色实线标记.

1.2 基于阶梯光栅的解复用器

在现有的片上MDM应用方案中，模分复用器/解复用器的设计通常依赖于非对称Y分支[13-14]、非对称定向耦合器(Asymmetric Directional Couplers,ADC)[15-18]、多模干涉(Multimode Interference,MMI)耦合器[19-20]和布拉格光栅(Bragg Gratings)[21-22]等器件. 基于上述器件设计一个独立的复用/解复用器,同时分离总线波导内的所有本征模式几乎是不可能的，通常需通过级联器件来实现3个以上模式的复用/解复用. 在WDM应用中，波长解复用器可以通过单个器件同时分离所有波长信道,例如阵列波导光栅(Arrayed Waveguide Grating,AWG)或阶梯光栅(Echelle Grating,EG). 图2是基于罗兰圆设计的阶梯光栅原理示意图.

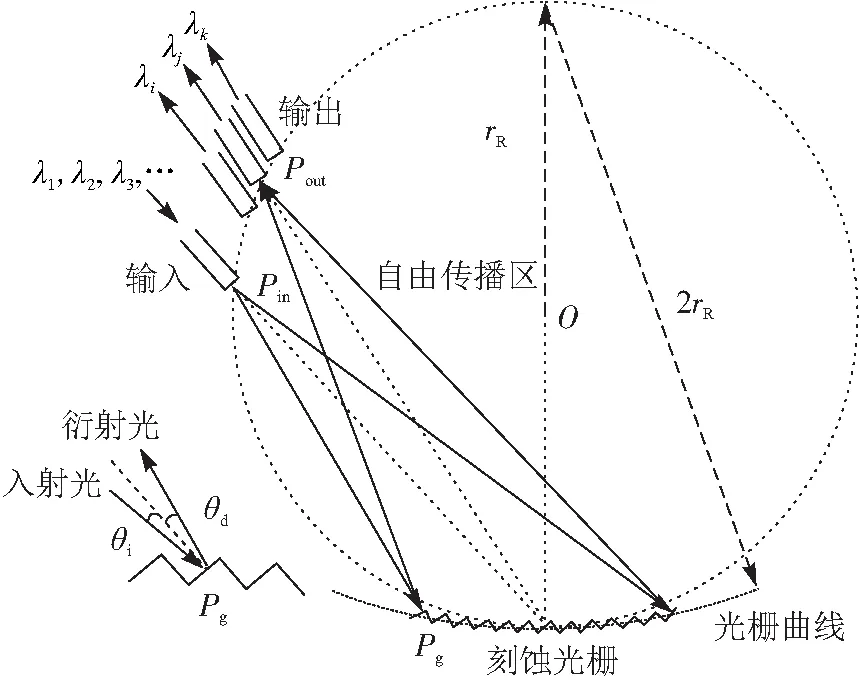
图2 应用于WDM的阶梯光栅解复用器的原理Figure 2 The principle of the echelle grating demultiplexer for WDM applications

光栅方程为

neffΛ(sinθi+sinθd)=m,

(1)

其中,θi和θd是入射角和衍射角；m是工作衍射级；Λ是光栅周期；neff是在自由传播区域(Free Propagation Region,FPR)中与工作波长相对应的有效折射率. 在纵向多模波导结构中，FPR中的2D平板波导在纵向方向上也是多模式的，输入波导中的高阶模在FPR中维持其高阶形态并通过光栅衍射后分离，因为不同模式对应的有效折射率提供了不同模式之间的相位差，这与横向多模的情况不同.

在前期研究[23]中，我们设计了一种基于阶梯光栅对3种纵向模式同时解复用的器件. 以硅波导中的准TE偏振为例，参考方程(1)可选取光栅各结构参数：入射角为35°，衍射级数为20，基模在波长为1 550 nm处的衍射角为32°，罗兰圆的半径为250 μm. 通过将一阶模和二阶模的折射率代入方程(1)，可分别计算出衍射角.

在MDM应用中，由于不能自由选择各模式折射率的差值，各模式的衍射角可能彼此远离，这会降低输出光谱响应的均匀性. 为提高光谱响应的均匀性，我们提出一种跨阶方案，不同模式可工作于不同衍射级(m)下[24]. 根据计算，将一阶模和二阶模的衍射级分别设置为19和18，可分别实现衍射角为31.44°和33.52°，相比之下，当衍射阶数保持恒定时与基模的输出角更加接近.

采用基尔霍夫标量衍射法[25]计算出3个模式通道的频谱响应(图3). 输入和输出波导分别使用绝热锥形波导展宽到2 μm，以便获得更好的光栅成像质量[26]. 尽管无法从频谱响应曲线中直接观测到各模式之间的串扰，但可以根据复用器的工作机制间接计算得出. 通过方程(1)可计算出，一阶模的图像以31.44°的角度聚焦，该位置与波长1 538.7 nm下的基模图像重叠. 它表示从一阶模泄露到基模输出波导的耦合效率等同于在波长1 538.7 nm下基模自身的输出效率.

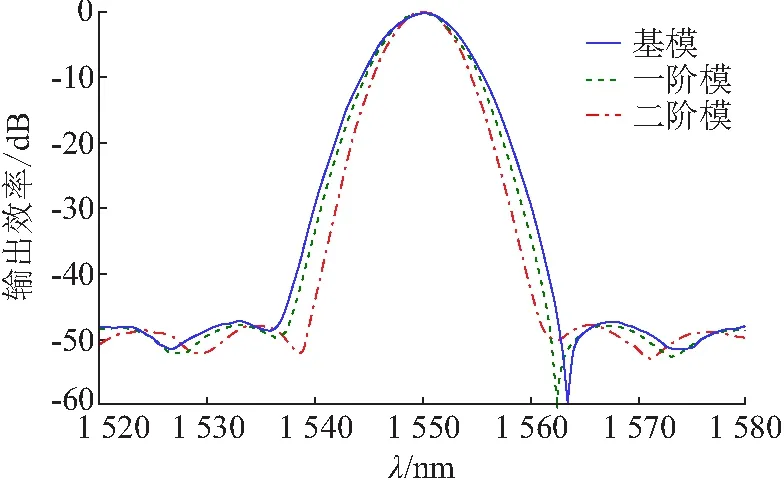
图3 前3个纵向TE模式的模拟输出光谱Figure 3 The simulated output spectra of the first three vertical TE modes under investigation

由图3可看出，该输出效率为-37.5 dB，即从一阶模到基模的串扰为-37.5 dB. 类似地，通过计算与二阶模衍射角对应的基模波长，可以求出二阶模到基模的串扰为-48.5 dB. 通过这种方式，可以进一步计算得出从基模和二阶模到一阶模的串扰分别为-38 dB和-50 dB，从基模和一阶模到二阶模的串扰分别为-49 dB和-53 dB. 由于本设计沿袭了阶梯光栅的低串扰特性，所以各通道间的串扰均很低.

在实际应用中，通常需要将MDM与其他复用技术(例如WDM或PDM)结合起来以实现更大带宽[11,27-32]. 这种混合系统可能会大大提高设计的复杂性. 然而，在阶梯光栅设计中，混合复用系统的布局同样简单与直接. 例如，当考虑用于WDM和MDM的混合系统时，波长差和模式折射率差都可提供相位偏移. 因此，对于具有特定波长j的第i模式，存在唯一的衍射角θij. 只需正确选择光栅参数即可同时解析所有通道. 文献[23]中提出的混合系统如图4所示，其中j个波长通道×i个模式通道可以同时进行多路分解，来自输入波导的所有j×i个通道将根据其衍射角重新聚焦. 此外极分复用(PDM)也可以通过相同的设计规则进行集成. 文献[23]中设计了3波长及3模式(共9个通道)的混合复用系统，3个波长分别为1 545、1 550、1 555 nm，3个模式同图3所选. 计算所得光谱响应如图5所示，为清楚起见，各模式的频谱依次下移10 dB以示区分.

图4 混合系统的示意图Figure 4 The schematic layout of a hybrid system

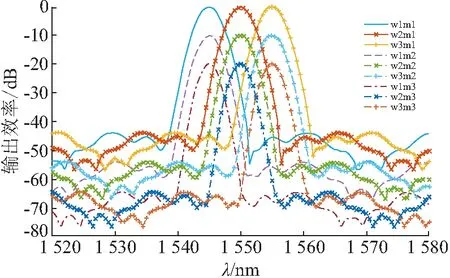
图5 所有3×3通道的模拟输出光谱Figure 5 The simulated output spectra of all 3×3 channels

注：“w” “m”后的数字分别代表波长、模式的数目.

1.3 基于非对称定向耦合器的解复用器

基于ADC结构设计的模式解复用器已得到了广泛的应用[15-18,33-35]，但是在使用纵向多模式时，情况会略有不同. 受制作工艺的制约，集成波导器件通常具有相同的高度，因而在发生耦合的2个纵向多模波导中，各自导模的对称中心在纵向方向上没有发生相对偏移(仍然重合)，这导致ADC的2个相邻通道中不同阶次模式之间的正交性没有被打破，2个耦合模式的重叠积分接近于0. 这意味着当波导具有相同的高度时，纵向多模式很难彼此耦合. 为了解决这一问题，一种方法是采用2个不同高度的条形波导组成ADC，利用2个耦合臂[36]；另一种方法是使用脊形波导作为ADC的其中一个通道，以打破对称性或正交性.

本文提出一个基于ADC纵向模式分离的简单示例，该ADC中一个耦合臂为常规条形波导，并由具有相同高度的脊形波导构成另一耦合臂，其横截面如图6所示.

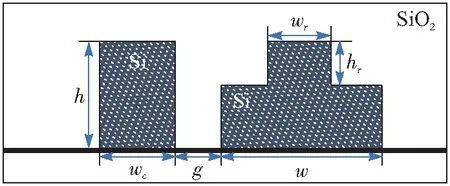
图6 ADC模式解复用器/转换器的横截面示意图Figure 6 The schema of the cross-section of the proposed ADC mode demultiplexer/converter

脊形波导的优点：即使在大尺寸下也可以通过调节波导参数以保持单模传输. 在以下计算中，只选取TM偏振，将中心波长设置为1 550 nm. 硅波导的高度h=1 500 nm，以容纳多个纵向导模. 2个波导的参数定义见图6，当考虑将条形波导中的基模耦合为脊形波导的基模时，将各波导参数选为：hr=800 nm，wr=500 nm，w=800 nm. 2个波导之间的间隙设为g=200 nm. 调节条形波导的宽度，以使待耦合的2个模式具有相同的相速度，即相同的有效折射率. 通过使用全矢量有限差分(FVFD)方法计算模式指数(令wc=614 nm). 经过优化，耦合长度选为160 μm. 对于从条形波导中一阶模到脊形波导中基模的耦合，可使用较小的脊形波导尺寸以减小耦合长度、缩短器件尺寸. 波导的各结构参数：hr=900 nm，wr=300 nm，w=500 nm，wc=527 nm，该情况下的耦合长度为78.5 μm. 图7给出了2种模式转换方式下主要电场分量的模拟结果. 通过上述2种转换方式的结合，可以实现条形波导中一阶模与基模的相互转换. 类似地，也可以通过同样的方式实现条形波导中基模与任意高阶模式的转换.

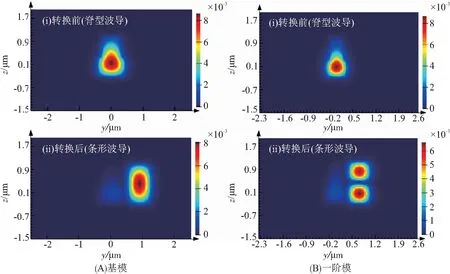
图7 从脊形波导中的基模转换为条形波导中基模和一阶模时器件横截面中的主要电场轮廓图Figure 7 The field profiles in the cross-section of the device when converting from the mode in the ridge waveguide to the fundamental mode and 1st mode in the channel waveguide

2 模式交叉器件

2.1 高效的多模交叉设计方案

在集成光学中，波导交叉是不可避免的，是大规模集成回路的必要组件之一. 在交叉区域，由于缺乏横向限制，透射光将会发散并导致传输效率降低和串扰增加. 特别是对于硅这样的高约束材料来说，波导中传输光场较大的发散角会导致明显的串扰. 因此，通常需要形成传输光束的聚焦图像或使用模式编辑方法将光束限制在相交区域中，可将散射的光强度降低到最小[37-45]. 现有的大多数研究主要针对单模波导，而对于多模波导则通常无法正常工作. 在MDM系统中，需要设计合适的多模波导交叉结构以优化系统布局. 此外，在兼具WDM和MDM的混合复用方案中，可能需要多模式交叉以建立无阻塞的光学交叉连接[46-47]. 文献[48]提出了一种解决多模式交叉的设计，采用优化的MMI耦合器可同时让2种导模交叉，但这种通过匹配成像距离的设计思路很难扩展到更多的模式中. 另一种设计引入鱼眼透镜对输入的多模成像，为横向多模提供高效的交叉[49]. 但该器件在面对纵向多模时会受到一些限制，因为对于不同的纵向分布模式，透镜焦距会随模式折射率的不同而发生偏移. 为了实现不同纵向多模的交叉，曲面反射镜可能是一种解决方案，因为它具有特定的几何特性，可以对不同的导模同时成像，从而为PIC提供了高效的多模交叉方案[50]. 这种器件的制造工序简单，不会引入任何额外的工艺步骤(如套刻).

2.2 椭圆形反射器实现单模式交叉

在前期研究中，我们借助椭圆形反射器来实现单个模式的交叉[51]，通过使用类似的器件形式设计了一种纵向多模交叉系统，并进行了相关的性能分析. 根据椭圆的性质，当光束从一个焦点入射并通过在椭圆边界全内反射时，由于从椭圆上任意一点到2个焦点的距离之和相等，因此在另一个焦点处将形成一个聚焦图像，并且可以利用1对椭圆形反射镜使光束在2次全反射后沿相同方向传播. 器件布局如图8所示，上椭圆和下椭圆形成1对椭圆. 第一椭圆形反射器的其中一个焦点与另一个反射器的一个焦点重叠. 来自焦点O1的入射光束汇聚在重叠的焦点O处，且在第二反射器的另一个焦点O3的输出端重新汇聚. 将这对椭圆形旋转90°，从而得到其他2个椭圆形反射器(左椭圆形和右椭圆形). 2束入射光的交叉区域位于所有椭圆的共同焦点O处.

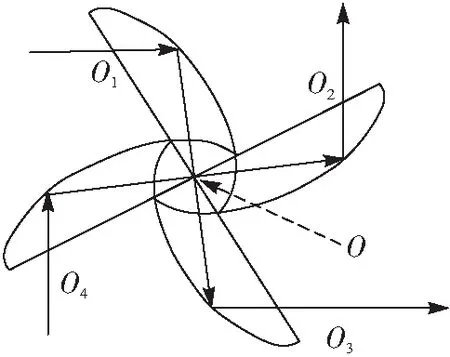
图8 椭圆形反射器的波导交叉结构示意图Figure 8 The schematic diagram of a waveguide crossing device using elliptical reflectors注：O1、O2、O3和O4是4个椭圆形反射镜的焦点，而O是共同焦点. 带有箭头的实线表示光束传播的方向.

2.3 纵向多模波导交叉的仿真结果

使用三维有限差分时域(FDTD)仿真计算所提出的纵向多模波导交叉的传输效率和串扰. 此处选择了SOI作为波导材料平台，并假设波导芯层被上包层SiO2覆盖. 在波长1 550 nm下，Si和SiO2的折射率分别取3.45和1.46. 多模波导的宽度和高度分别为400、1 500 nm. 根据椭圆的成像规则，通过解析计算可获得椭圆反射器的参数[51]. 椭圆的半长轴为12.3 μm，半短轴为8.7 μm，焦距为17.4 μm. 在仿真中，使用锥形波导将输入和输出波导的宽度从400 nm增加到大约1 μm时，器件的成像性能得到明显改善. 因此，在以下FDTD仿真中，输入波导和输出波导的宽度都设为1 μm. 仿真得到的场分布如图9所示.

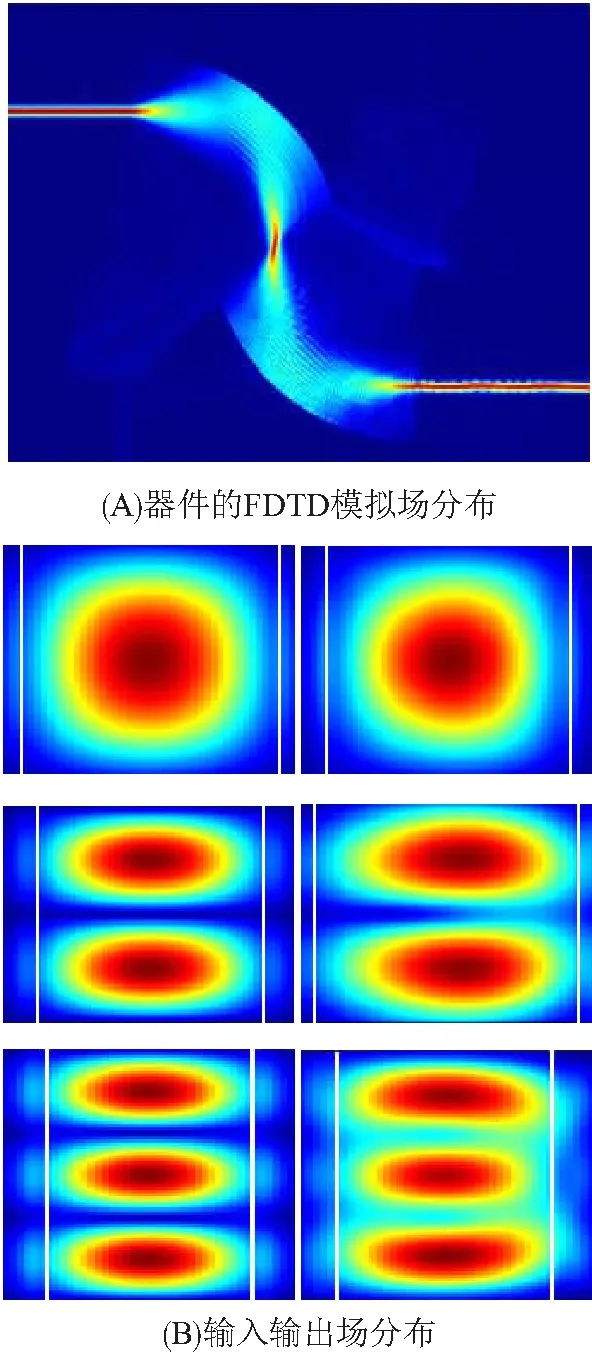
图9 器件的FDTD模拟以及输入/输出波导的场分布Figure 9 The field profiles of the proposed device simulated with FDTD and the input/output waveguides注：B图中输入和输出波导的宽度均为1.0 μm.

2.4 纵向多模波导交叉的性能

计算得到基模的额外损耗和串扰分别为0.21、-42.8 dB，这比直接使用直波导交叉的效率高. 为了验证该设计对于纵向多模的操控能力，计算工作于高阶模下的器件性能. 一阶模和二阶模额外损耗分别为0.21 dB和0.33 dB，且基模、一阶模和二阶模的串扰均低于-40 dB. 高阶模损耗和串扰与基模的基本接近，不存在显著差别. 在整个C和L波段，使用相同椭圆形反射镜的参数计算各纵向模式下的交叉性能(图10)，可以看出，该器件具有相对较大的带宽，这是其独特优势之一，特别是考虑到还需要用在具备WDM器件的混合复用系统中.

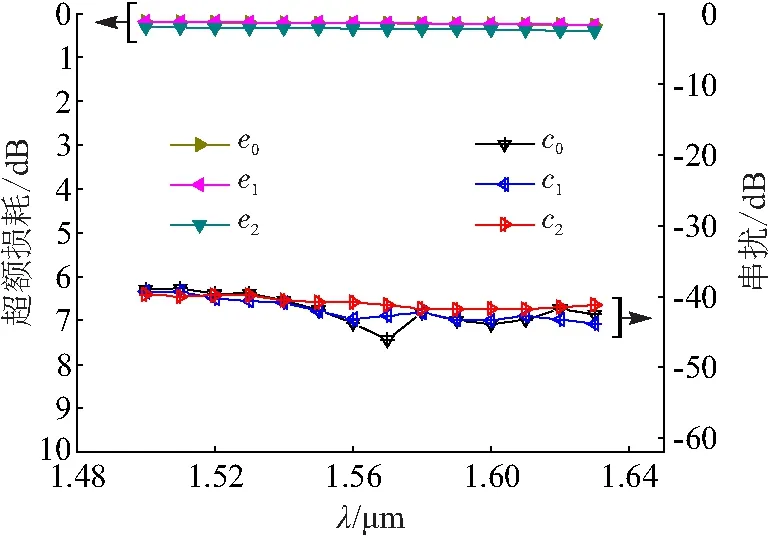
图10 3种准TE模式的额外损耗和串扰与波长的关系Figure 10 The excess losses and crosstalks of the first three quasi-TE modes as functions of the wavelength注：e0、e1、e2表示基模、一阶模和二阶模的额外损耗；而c0、c1、c2分别表示它们的串扰.

3 结论

研究了一些可用于纵向多模硅基纳米波导的片上光子集成器件，具体包括：提出了一种基于阶梯光栅的模式解复用器，可以同时分离包括不同波长及模式等共9个信号通道，所有通道的串扰均达到-30 dB以上；设计了基于脊形波导的ADC结构，展示了纵向多模波导中基模及一阶模与脊形波导中基模的相互转换；提出了基于椭圆反射面的多模式交叉的器件，计算结果显示，该器件至少可支持基模、一阶模及二阶等模式的同时交叉，且各模式交叉时的串扰均能达到-40 dB左右的优异水准.