基于大学数学语言向自然语言过渡的一些思考
(陆军步兵学院基础部 江西·南昌 330103)
由于数学学科追求精确性和高度概括性的特点,决定其需要发展自身特有的语言来描述其内涵。在数学教材里充满了特定的术语,统一通用的符号等等,这些都属数学语言的范畴。数学语言与我们习惯的自然语言大相径庭,其具有的抽象属性,无疑增加了学生们的理解难度。
1 数学语言的内涵和作用
在数学教材中布满了大量的数据、术语、图形、表格以及符号等等,它们构成了数学语言并承载着数学知识。比起自然语言,数学语言有着能够准确描述数学中各种对象的优势,它克服了自然语言在表达上的含混不清。但是,数学语言明显不如自然语言通俗易懂,形象直观。所以教师授课时,一定要把握可接受原则,只有在学生形成一定理解的基础上,才能继续发掘更深层次的数学内涵。
我们的学生就读中小学期间,因应试的需要,许多教师在数学教学上更为侧重对各类题目的梳理、求解和归纳,而淡化对基本概念,基本定理以及基本数学符号的解析。这使得学生们对数学产生片面化,套路化和庸俗化的理解。同时采用“刷题”的方式,也使学生们的数学语言运用不够,理论基础不牢。当面对更加精炼,更加抽象的大学数学语言时,学生们领悟起来就非常吃力。
针对上述现状,教师在大学数学教学中,很有必要把抽象难懂的数学语言转化成具体易懂的自然语言。本文以高等数学课程里常见的一些术语和符号为例,具体讨论如何把它们从数学语言层次过渡到自然语言形式上来。
2 数学语言向自然语言转化实例
2.1 术语的转化
数学术语是介绍数学中定义,定理等产生的专有名词,它分为两类,一类是具有实际意义的术语,比如等差数列;一类则是纪念在某领域有过伟大成就的数学家并以他们的名字来命名的术语,比如微分学里的柯西中值定理。对术语的充分理解,可以使学习者事半功倍。下文就一些常见数学术语,举例说明。
2.1.1 极限保号性
高等数学中极限概念的引入为研究函数的分析性质提供了有力的工具。然而它的定义和性质,成为了学生们学习时的“拦路虎”。如探究极限保号性时,“保”代表什么,“号”是谁的号?定理内容往往使学生感到晦涩难懂。教师应该做到清晰通俗地表述,“在函数极限存在的前提下,极限值号的正或负,可以保证在某一局部范围内对应函数值的号同正或同负”。然后再配合相应的几何直观加以说明。这要比直接灌输抽象的数学语言定义,更易使学生接受。
2.1.2 间断点
关于间断点,很多老师这样来讲解,可按左,右极限是否都存在,分为第一类和第二类间断点;若存在,又可按左,右极限是否都相等,把第一类间断点分为可去间断点和跳跃间断点。但“可去”具体指什么,“跳跃”又是何意,却并没有引起相应的注意。“可去”意味着补充或修改函数在间断点处的函数值,使其等于左,右极限值,该函数就成了连续函数,该类间断点可去除而成连续点,“跳跃”指的是函数图像在间断点处呈现跳跃式的断开,无论怎样补充或修改定义,都不可能使在该点处的函数值同时等于左,右极限值,该类间断点不能去除而使函数连续。这样通俗说明一下,对初学者理解术语的益处在于形象直观,便于认知。
2.1.3 驻点
不论是教师教学,还是学生学习,大多都只关注一句话“使导数值为零的点是函数的驻点”,就把这个概念一带而过。实际上它在数学,物理等学科中都有应用。驻点(Stationary Point)又称平稳点、稳定点或临界点(Critical Point),通俗来理解驻点就是在“这一点”处(注:驻点并不是平面上某点,而是这点处的横坐标值)函数输出值停止增大或减小。
从几何角度看函数的图像在驻点处趋于平缓,停止变化。对于一元函数,驻点处对应切线平行于x轴;对二元函数来说,驻点处对应切平面平行于xoy面。从物理角度讲,临界点(驻点)表示物体由一种状态变到另一种状态,所要满足的条件。比如电容器充放电时的电压。依据驻点在数学上是函数可能的极值点这一理论,在某些情况就可迁移到物理中,建立临界点与取最值点之间的联系。教师这样解释术语,就使得驻点的概念不再孤立,而是与后续学科搭起了桥梁。
2.1.4 中值定理
“中值定理”这一节内容出现的多是带有人名的术语,其重要意义在于为导数的应用奠定了基础。该节内容抽象度高,理论性强,学生们学习起来异常困难。
从逻辑角度出发,教师可采用问题教学法来设置一系列与内容具有密切联系的问题。比如,由历史上对最值问题的研究来引出费马(Fermat)定理,再利用所得结论引出下一个问题“究竟满足什么条件的函数,一定存在驻点?”由此导出罗尔(Rolle)定理的内容,通过讨论“若去除罗尔定理中,区间端点值相等这一较强条件,原有几何直观及相应结论又会如何变化?”引出拉格朗日(Lagrange)中值定理,再讨论“若函数以参数方程形式给出,拉氏定理的结论又会出现哪些变化?”进而推广到研究两个函数情形的柯西(Cauchy)中值定理。当学生知悉内容之后,教师还需“打铁趁热”引导学生构建知识链条,把握微分学中这三大中值定理的联系,使学生领悟这种从特殊到一般的逻辑衔接和思维跃迁过程。
从历史角度出发,中值定理的发展,由最初的萌芽到最终的完善,经历过这样几种形式。首先是卡瓦列里(Cavalieri)和阿基米德(Archimedes)给出的几何形式的微分中值定理。接着罗尔研究了代数形式的微分中值定理,后来,随着极限、连续、导数、微分等定义的相继严格化。拉格朗日,柯西等一批数学家给出了严格的分析形式的微分中值定理。教师在助力学生理解中值定理内容时,应从几何、代数、分析的角度加以通俗注释,这样不仅是对内容的全面解析,更是与中值定理的历史发展脉络相契合。同时中值定理形式的发展,内容的逐步精确严格化,也体现着逻辑与历史的辩证统一。
2.2 符号的转化
数学符号作为一种记号用来表示数学中的概念、关系等等,它是一种含义极具概括,形体非常浓缩的特殊的数学语言。对数学符号的理解不到位,新旧符号易混淆等等原因,易使学习者产生厌学,畏难情绪。教师有必要加强符号教学的设计,多用自然语言解析符号的含义。下文中将通过“高阶无穷小”符号,“中值”符号等例,列举说明。
2.2.1 高阶无穷小的符号“o”
在高等数学中,当函数极限存在时,函数可以转化成它的极限值加上无穷小,其作用是“游离”出极限号里的函数,把从研究一般极限转到研究特殊极限(无穷小)上去;无穷大的情形也可转化成研究无穷小来考虑,所以研究无穷小量意义重大。我们知道对任意两个实数,可通过作差或作商的方式比较它们的大小。而对于两个无穷小量,作差取极限仍是无穷小量,故可通过作商取极限来比较它们趋于零的速度,基于此数学中引入无穷小比较的概念。而高阶无穷小是其代表情形,若明白其意义,对低阶无穷小,同阶无穷小,等价无穷小等概念都会迎刃而解。
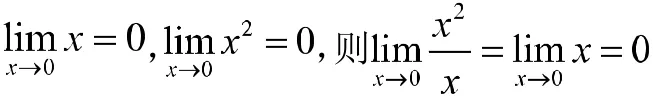
从以函数形式呈现的零点定理,介值定理。到以导数形式呈现的中值定理。再到以积分形式呈现的中值定理。尽管表达式各异,但是这些定理有一个共性的地方,它们的结论里面一定与所讨论的区间(a,b)中的某一个点(值)有关,这个点(值)统称为中间点(值)。数学上,我们用符号“”来表示中间点(值)。
学生们常常感觉这个符号,弯弯曲曲,别扭难写。作为教师应强调该数学符号的重要性,讲清符号产生的前因后果。因为古希腊很多数学家的杰出贡献,所以希腊字母在数学中广泛应用。国际上统一约定符号“”表示区间内的一个未知特定值。
值得注意的是,和中间值有关的定理,大多是没法准确知道这个“中值”到底是多少,不少学生对此会有疑惑,教师则需要说明“中值”的存在意义,即使不知其精确数值,但它的客观存在性对定理的结论,对实际的应用并不影响。在这里,教师可用一句古诗“只在此山中,云深不知处”,通俗来描绘中间值(点)这种“存在的意境”,用符号抽象之美与诗句文学之美相融合的过程,来引起同学们的学习兴趣。
导数是高数中重要的概念,其内容复杂抽象,其符号形式多变,初学者很难真正通晓其义,因此要求教师须把抽象定义通俗化,讲清各个符号历史来源及演变,让学生理解导数全貌。可从几何、物理、经济、军事等角度来通俗理解,在几何上,导数表示切线的斜率;物理上,导数理解为物理量变化率(如在某一时刻瞬时速度,瞬时功率等);经济上,“边际”,“弹性”成为导数的代名词(边际成本,供给价格弹性等都有相应各自函数的导数表达);军事上导数体现在军事量变化率(如在某一时刻兵员伤亡率,弹药损耗率等)。无论模型如何变化,这些事例的共性都是函数在某一时刻的瞬时变化率问题,在数学量上有统一的表达形式,即通俗地理解导数的本质就是“增量比的极限”(注:增量比虽形式多样,但本质相同)。
3 结语
对大学数学中术语的通俗解释,符号的寻根溯源,旨在使学生对数学有清晰的理解和良好的认知。当学生具备了一定的学科基础和认知基础之后,教师还要引导他们再回归到数学语言层面,在感受到数学语言严谨精确的同时,学生的逻辑思维也会得到锤炼和升华,体会到其中散发的抽象之美,学生们自然而然就不再畏惧数学。

