多级轴流式膨胀机的多学科优化设计*

王国欣 郭 伟 邵伟龙 任霁筇 刘凤祺 闻苏平＊

（1.西安交通大学能源与动力工程学院；2.沈阳鼓风机集团股份有限公司）

0 引言

膨胀机作为有机朗肯循环等工业余热回收系统中实现热能转换为机械能的核心动力部件，国内、外研究人员对此进行了长期深入的研究。Moroz[1]等人对以R245fa为工质的250kW功率有机朗肯循环系统膨胀机在150℃以下低温工况下的详细设计进行了讨论，重点介绍了膨胀机流道、气动和结构设计的细节并强调了级数、泄漏和叶片扭曲等关键参数对膨胀机效率的影响。Jubori[2]等在小型单级亚音速轴流膨胀机中，在应用6种工质条件下，采用多目标遗传算法对轴流膨胀机叶片数、叶片前缘角、后缘角和叶片安装角等8个设计参数进行优化，使轴流膨胀机与基准设计工况相比，最大绝热效率提高了14.08%，突显三维优化技术在提高轴流膨胀机性能方面的技术潜力。陈朝辉[3]等人基于有限元法，对涡轮机叶轮及叶片进行了模态分析，研究获得了叶片旋转的动力特性并提出叶片动频不能小于3.5倍基频的设计准则。

轴流膨胀机的工程优化设计流程如图1，首先建立轴流膨胀机气动数值计算模型，进行气动数值分析，根据轴流膨胀机叶栅的气动性能进行单目标或多目标优化，再进行结构设计，对动、静叶片的强度和动力特性进行优化，由于气动与结构性能存在一定的制约关系，这种优化策略可能无法获得合理的结构方案，而需要重新对动、静叶栅进行气动设计，就大大增加了优化设计的时间成本。本文利用某5MW有机朗肯循环膨胀机建立了一个多级轴流膨胀机的跨学科优化平台，对轴流膨胀机的多列动、静叶栅同时进行气动与结构的多学科与多工况优化，快速获得综合性能提升的优化设计方案。

图1 膨胀机工程优化流程图Fig.1 Engineering optimization flow chart of expander

1 多级轴流膨胀机多学科优化平台

多级轴流膨胀机的优化平台主要由几何识别及参数化、气动数值计算、结构数值计算和优化算法几大模块组成；几何识别及参数化模块用于对原型轴流膨胀机的气动模型和结构模型按照一定的参数化规则进行逆向几何识别，将几何设计参数提取至参数池；气动数值计算模块包含气动计算域提取、网格划分与数值求解，并将数值求解的温度场与压力场传递至结构数值计算模块实现单向流固耦合。提取膨胀机总-静绝热效率ηts和轴向推力F作为优化参数加入参数池；结构数值计算模块包含固体计算域提取、网格划分、强度求解、动力特性求解，提取动叶片最大等效应力S和最大径向位移A，并加入到参数池；优化模块将参数池中的设计变量进行数值边界和数值类型定义，将优化变量进行优化目标定义和数值约束，利用多目标遗传算法MOGA（Multi-Objective Genetic Algorithms，MOGA）进行优化。此优化平台可对多级轴流膨胀机的多工况和多列动、静叶栅同时进行优化，自动进行模块间数据传递，形成工作流，实现多学科和多目标优化设计，优化平台的架构图和流程图如图2所示。

图2 优化平台架构图和流程图Fig.2 Optimization platform flow chart

2 多级轴流式膨胀机叶栅参数化方法

原型轴流膨胀机动、静叶栅采用平面流面的二维叶栅积叠，使用等中径端壁型线进行截取，通过调整流道宽度可快速实现机组模化设计，如图3所示（图中蓝色代表静叶片，红色代表动叶片）。叶片的空间形状由沿叶高方向11个截面所确定，将每个截面的二维叶栅使用由Pritchard[4]改进的八参数法定义。动叶和静叶的中径截面的基本几何参数见表1。叶片的压力面和吸力面一般常采用多阶贝塞尔曲线[5]定义，n个曲线控制点存在2n个设计变量，经过研究改进，将曲线采用多阶B样条曲线[6]定义，引入向量因子作为设计变量，利用向量运算可使n个曲线控制点存在n+1个设计变量，对于高阶曲线可大幅减少设计变量数目，大大减少了压力面、吸力面曲线相交等无效方案的几率。控制点定义方式见图4，CAESES[7]平台下向量运算式为：

图3 原型机叶栅造型方式Fig.3 Original blade cascade

表1 原型轴流膨胀机叶栅中径截面设计参数Tab.1 The design parameter of cascade pitch section of axial expandar

图4 二维叶栅曲线控制点定义方式Fig.4 2D blade control point

为了减少设计变量的数量，动叶和静叶的空间定义仅选取沿叶高方向0%，25%，50%，75%和100%，5个截面，每个截面处的压力面和吸力面的B样条曲线控制点向量因子Tp1，Tp2，Tp3，Tp4，Tp5，Tp6作为一组设计变量；动叶和静叶的切向积叠线采用B样条-直线-B样条曲线的方式定义。静叶采用前缘积叠，动叶采用重心积叠，叶根截面端点固定不动，存在积叠线各控制点Tvc1，Tvc2，Tvp1，Tvp2，Tα1，Tα2，Tα3，具体定义方式见图5。

图5 切向积叠线Fig.5 Stack line in tangential

3 多级轴流式膨胀机数值计算方法

3.1 气动数值计算方法

原型轴流膨胀机由两级叶栅组成，单主流区域包含两列动叶和两列静叶共计四列叶片，如图6所示。计算域沿介质流动方向由进口静止区域（延长段）、静止区域、旋转区域、静止区域、旋转区域和出口区域组成。

图6 计算域Fig.6 Computational domain

轴流膨胀机三种工况如表2所示，进口静止区域给定总压、总温和介质流向，出口给定静压，叶片采用单通道周期性边界，旋转区域设置转速，计算域内所有固体壁面均为光滑、绝热、无滑移，动静交界面使用混合平面法。动叶叶顶间隙与固体壁面一般连接，旋转区域叶顶侧壁面与出口区域两侧固体壁面在相对坐标系下设置反向旋转。

表2 膨胀机三种工况参数Tab.2 Three kinds of design condition parameters of expandar

数值计算采用有限体积法离散求解三维定常可压缩的雷诺时均N-S方程，湍流模型为两方程的SST模型[8]，近壁面采用自动壁面函数，气体介质为R245fa。

计算域的空间离散使用结构化网格，拓扑结构为H-O-H，叶片周围采用O型网格，向外过渡为H型网格，动叶叶顶间隙采用蝶形网格，如图7所示。近壁面网格作加密处理，最大延展比1.3，粘性底层至少设置10个节点，进口静止区域和出口区域处延展比1.02。保证计算域网格最大长宽比小于1 000，正交度15°～165°，网格质量能够确保计算精度。全局残差均方根值RMS的值小于10-4，计算域进出口质量流量之差小于0.5%则视为计算收敛。

图7 数值计算网格细节Fig.7 Details of grid

图8 网格无关性验证Fig.8 Grid independence verification

图8所示是y+≈30与y+≈1使用自动壁面函数，1×106,2×106和4×106三套不同网格数所得到的三种工况的相对功率-效率曲线，考虑到计算的精确性和效率，最终使用了y+≈30，2×106个节点的网格来进行数值计算与优化。

3.2 强度与动力特性数值计算方法

多级轴流膨胀机动叶片强度与振动采用有限元方法，原型膨胀机动叶的轮盘和动叶片整体铣制，轮盘最大等效应力和变形均远小于动叶片相应值，因此忽略轮盘，建立动叶有限元模型并考虑叶根圆角。该膨胀机动叶材料属性如表3所示。

表3 动叶材料特性参数Tab.3 The dynamic blade material parameters

约束动叶叶根表面所有自由度，添加轴向旋转速度3 000r/min。图9所示为第一级动叶离散化的固体计算域，网格为四面体非结构化网格并在叶根圆角进行局部加密；将CFD计算获得的动叶叶片的压力场与温度场加载到对应固体计算域，计算获得了在最大膨胀比工况（工况3）下动叶片最大应力和位移，如图10所示。网格分别采用了第一级动叶5×103，1×104和1.6×104及第二级动叶8×103，1.4×104和2×104三套方案。图11所示为采用三套网格在工况3下计算获得的膨胀机两级动叶的无量纲最大应力和应变，可以看到，采用三套网格计算结果基本相同，考虑到精度及计算效率，最终采用了第一级动叶1×104和第二级动叶1.4×104的网格。最后求解了预应力处理下两级动叶的前六阶模态，用于判定优化后动叶片的工作转速频率激励与静叶通过频率激励。

图9 动叶片四面体网格Fig.9 Rotor blade tetrahedral grid

图10 动叶片加载压力、温度场Fig.10 The pressure and temperature field of dynamic blade

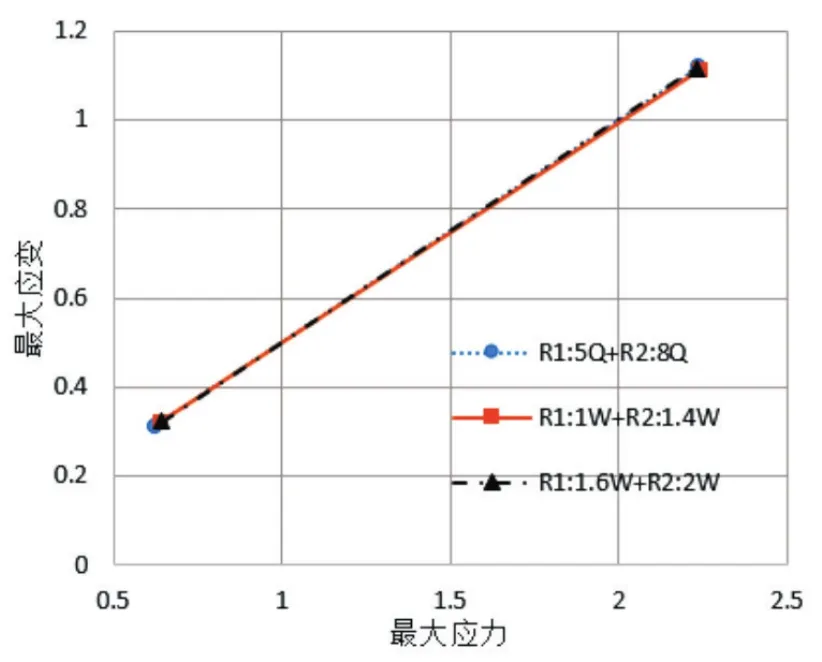
图11 网格无关性验证Fig.11 Grid independence verification

4 多级轴流式膨胀机多学科优化方法

4.1 数学描述

本次轴流膨胀机的优化参数为三种工况下的总-静效率ηts、轴向推力F、动叶最大等效应力S和动叶顶最大径向位移A，将三种工况下的ηts最大化，F最小化，约束最大膨胀比工况（工况3）下的Sc3小于830MPa，Ac3小于0.9mm，约束三种工况下ηts大于初始值，F均小于65kN，质量流量m变化均小于2%。该问题目标函数的数学描述如下：

对于设计变量X集合元素，需定义各自的上下边界，描述单一叶片形状的设计变量X=(Tp1i,Tp2i,Tp3i,Tp4i,Tp5i,Tp6i,Tvc1,Tvc2,Tvp1,Tvp2,Tα1,Tα2,Tα3,i=1,2,3,4,5)，共计 37 个设计变量，两级轴流膨胀机共有动、静叶片四列叶片，共计148个设计变量。

4.2 优化方法

将多级轴流膨胀机的多学科多工况优化问题转化为一个多目标优化的数学问题。因变量数较多，通过空间取样建立映射关系良好的数学代理模型，需要数量庞大的样本点，是几乎不可完成的。因此，优化方法直接使用多目标遗传算法（MOGA）进行两轮优化的策略[9]，第一轮优化针对叶片积叠线造型，侧重于全局寻优选取动静叶栅耦合较好的倾、弯规则，第二轮优化针对叶片沿叶高方向五个截面的压力面吸力面控制点，在首轮优化后所得最优叶片积叠规则的基础上寻找二维叶型的最优解，图12为多目标遗传算法流程图，设置初始人口数为20，最多进化20代，每次进化生成10人口，多点交叉，交叉率50%，变异率20%。

图12 多目标遗传算法流程图Fig.12 MOGA workflow chart

5 多级轴流式膨胀机优化结果与分析

5.1 优化方案及分布规律

经过两轮约420次迭代计算，选取了54个非劣解集中的一个作为最优解，如表4中所示，工况1的总-静效率ηc1.ts提高了1.23%，输出功率Wc1提高1.1%，轴向推力Fc1减小4.5%，工况2的总-静效率ηc2.ts提高1.44%，输出功率Wc2提高1.6%，轴向推力Fc2减小2.5%，工况3的总-静效率ηc3.ts提高1%，输出功率Wc3提高0.67%，轴向推力Fc3减小3.4%，三种工况下质量流量变化m均小于1%，R1和R2动叶的最大等效应力S均未超过表3中的材料屈服极限。工况1为有机朗肯循环的设计工况，工况2和工况3分别为夏季和冬季时循环中凝汽器冷却水温度变化，导致上游膨胀机不同总静膨胀比[10]的运行工况，将两级轴流膨胀机优化前后的性能绘制成特性曲线，见图13。

表4 优化前后性能参数对比Tab.4 Comparison of performance parameters before and after optimization

图13 两级轴流膨胀机三种工况性能曲线Fig.13 Two stage axial expander performance curve

图14为多维空间中两级动、静叶栅总-静效率ηts的分布图，图14（a）中可发现较高的第二级总-总效率η2.tt对应了较高的整体总-静效率ηts，第二级效率对整体效率影响较大，而第一级效率η1.tt与整机效率的影响并不明显；图14（b）中可见在第二级反动度Ω2在0.25～0.3时，第一级反动度Ω1在0.46～0.52大范围内可以获得较高的第二级总-总效率η2.tt和整体效率ηts，第一级反动度Ω1在0.5～0.52时，高效点比较集中；图14（c）中可发现对于第二级动叶，尾缘出口马赫数MR2.te在0.8～0.84，出口气流角αR2.te约在-58°时，可获得较高的第二级总-总效率η2.tt和整体总-静效率ηts，在此范围内马赫数MR2.te越高，效率越高。

将叶片弯曲和倾斜方向朝向吸力面定义为正弯和正倾，朝向压力面定义为反弯和反倾。图15（a）和图15（b）分别为整机总-静效率随R1动叶和R2动叶的弯曲形式分布情况，蓝色圆点为满足约束的非劣解集，红色为选取的优化方案，结合图2可知当Tα1＞0时，叶片下半部呈正倾或正弯，反之为反倾或反弯，Tα3＞0时，叶片上半部呈正倾或正弯，反之为反倾或反弯。可发现R1动叶下半部正弯20°和40°时，高效点较为聚集，R2动叶下半部反弯-10°左右，上半部正弯45°时高效点比较集中；图15（c）和图15（d）分别为R1动叶和R2动叶的最大应力随弯曲形式分布情况，可发现R1和R2动叶类似，均在叶片的下半部正弯20°～40°时，最大等效应力较大。

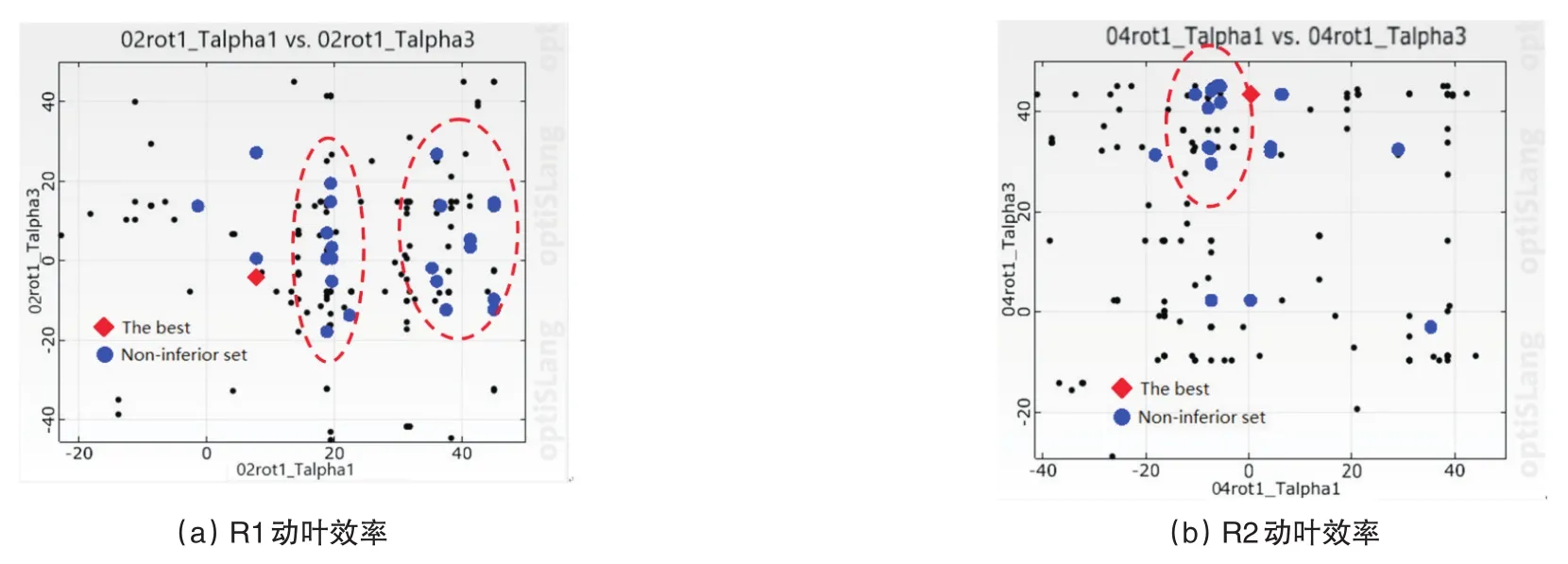
图15 动叶弯曲分布图Fig.15 Bend blade distribution chart

5.2 气动性能分析

图16为原始叶片与优化后叶片的对比，可以看到S1，S2静叶和R2动叶优化后均呈反弯，R1动叶为正倾加顶部正弯，呈倒J型，图17（a）与（b）为工况1下子午面压力梯度和熵分布图，可发现由于压力梯度与流速的影响，R1动叶片正倾加正弯曲在通道内形成J型压力梯度，使叶顶端壁附面层及叶中主流区向叶根端壁迁移，改善了叶顶端壁损失和叶中的二次流损失，而叶根附面层增厚，流动恶化；S1，S2静叶和R2动叶反弯曲会在通道内形成反C型压力梯度，使叶中主流区向两侧端壁迁移，减少叶中二次流损失，增加端壁侧的流动损失；从图17（b）中可以看到，优化后叶中主流区低熵产区面积增大，二次流损失减小，S2静叶叶顶高熵产区消失，端壁损失减小，R2动叶后叶顶一侧高熵产区增大，端壁损失增大。

图16 优化前后叶片对比Fig.16 Blade row comparison

图17 子午面压力梯度及熵分布Fig.17 The distribution of meridional pressure gradient and entropy

表5为各列叶片能量损失系数对比，可看到三种工况优化情况类似，与图13（b）相对应，S1、S2静叶和R2动叶损失减小，R1动叶损失增大，通过动、静叶片倾、弯规则的耦合，可达到局部级损失增大，但整机损失减小，总效率提高的优化目的，定义能量损失系数定义如下：

表5 各列叶片能量损失系数对比Tab.5 Blade energy loss coefficient comparison of blades

其中，h01为静叶进口总焓；h2为静叶出口静焓；h2S为静叶出口绝热静焓；h3为动叶出口静焓；h3S为动叶出口绝热静焓；h02,rel为相对坐标系下动叶进口总焓。

图18为能量损失系数沿叶高方向分布曲线，各列叶片在三种工况的能量损失优化前后趋势均相似，图18（a）中S1静叶20%叶高以下与80%叶高以上的两侧端壁面损失增大，叶中主流区损失减小，这与图17中S1静叶优化后的反弯形式流体迁移特点相一致；图18（b）中R1动叶80%叶高以下部分损失增大，以上部分损失减小，R1动叶优化后顶部为正弯，整体呈倒J状，顶部损失减小与正弯形式叶片的特点相一致；图18（c）S2静叶与图18（d）中R2动叶的50%叶高以下均损失增大，以上部分损失减小，是由于R1动叶顶部正弯与S2静叶、R2动叶反弯形式耦合后，产生指向叶片下部区域的正压梯度，使流体向叶根侧端壁面进行迁移，改善了叶片上部区域的流动情况。

图18 能量损失系数沿叶高分布Fig.18 The distribution of energy loss coefficient along the blade height spanwise

5.3 强度分析

轴流膨胀机运转时，叶片受离心载荷、热载荷和气动载荷等多种因素影响，叶片上会产生拉伸和弯曲应力，根据第四强度理论，叶片最大等效应力大于材料屈服强度将产生塑性变形；当动叶的最大径向位移大于叶顶安装间隙时，动叶将与端壁发生刮碰导致断裂。

工况3下两级动叶的最大等效应力见图19，数值均小于材料屈服强度，R1动叶最大应力出现在叶根吸力面最大叶厚处，而R2动叶最大应力出现在约30%叶高的尾缘处，并且在前缘处也出现较大的应力分布。

两级动叶的最大径向位移见图20，R1动叶为0.012mm，处于动叶50%叶高以上的前缘处；R2动叶为0.573mm，处于动叶叶顶尾缘。

图19 最大等效应力云图Fig.19 Maximum equivalent stress

图20 最大径向变形云图Fig.20 Maximum directional deformation

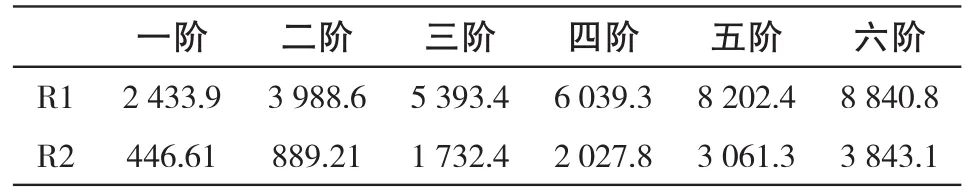
表6 动叶片前六阶固有频率Tab.6 The dynamic blade first six order natural frequency

5.4 振动分析

轴流膨胀机叶片的振动产生的主要原因是周期性的机械激振与叶片流道气流尾迹激振[11-13]，机械激振力来源于膨胀机的主轴旋转，而气流尾迹激振来源于当前叶片上下游的交变气流，当激振频率与叶片固有频率呈倍数关系时，叶片与激励源发生共振，严重时导致叶片疲劳断裂[14]。计算得到的两级动叶片前六阶固有频率如表6。

图21和图22为两级动叶的前六阶振型图，对于R1动叶，一阶振型为切向弯曲振动，弯曲发生在叶顶；二阶振型为扭转振动，扭转最大变形发生在叶顶尾缘；三阶振型主要为轴向弯曲振动，弯曲最大变形量出现在叶中尾缘；四阶振型为二阶切向弯曲振动；五阶振型为二阶切向弯曲与二阶扭转复合振动；六阶振型为三阶切向弯曲振动。R2动叶的一阶振型为切向弯曲振动，二阶振型为扭转振动，最大变形发生在叶顶尾缘；三阶振型为扭转复合振动，主要为一阶扭曲振型；四阶振型为二阶切向弯曲振动；五阶六阶振型均为高阶弯曲振动。

图21 R1动叶前六阶振型图Fig.21 R1 dynamic rotor blade first six order vibration mode

图22 R2动叶前六阶振型图Fig.22 R2 dynamic rotor blade first six order vibration mode

激振频率与叶片固有频率（动频）呈阶次倍数关系时，叶片会以当前阶次振型发生最大振幅共振，因为峰值附近的振幅依然较大，还需要设定安全避开率；高阶振动振幅较小，危害相对较小，因此对于低频激振，一般取二到六阶次[15]。低频激振力避开率见公式（6），高频激振力避开率见公式（7）：

其中，Δf为避开率；K为阶次，取2～6；fz为激振频率；fn为动叶片固有频率；Z为上下游静叶数量；Zfz即静叶栅通过频率。

根据动叶片前六阶模态振型，取不同的安全避开率，将激振力干涉范围与动叶前六阶固有频率绘制到图表中，见图23（a）～（d），可见R1，R2动叶前六阶固有频率均未落入工作转速干涉和静叶通过频率干涉区域，不会发生大幅度振动，判定结果合格。

图23 R1，R2动叶前六阶固有频率判定Fig.23 R1，R2 dynamic rotor blade first six order natural frequency

6 结论

通过建立以多目标遗传算法MOGA为基础的的两级轴流涡轮多学科多工况优化平台，在维度庞大的设计空间中寻求最优解，得到了在气动和结构多方面综合评估得到提升的方案。

通过对5MW有机朗肯循环系统中的两级轴流膨胀机的优化，获得如下主要研究结论：

1）对十一参数法叶栅定义方式改进的八参数法进一步研究，对动、静叶片的压力面、吸力面曲线采用多阶B样条定义，引入向量因子并作为设计变量，可大幅减少设计变量数目，同时建立控制点二维拓扑，减小曲线相交等无效方案的发生几率。

2）两级轴流膨胀机的第二级效率η2.tt对整体效率影响较大，而第一级效率η1.tt与整机效率的影响并不明显；第二级反动度Ω2在0.25～0.3时，第一级反动度Ω1在0.46～0.52大范围内可以获得较高的第二级总-总效率η2.tt和整体效率ηts，第一级反动度Ω1在0.5～0.52时，高效点比较集中；对于第二级动叶，尾缘出口马赫数MR2.te在0.8～0.84，出口气流角αR2.te约在-58°时，可获得较高的第二级总-总效率η2.tt和整体总-静效率ηts，在此范围内马赫数MR2.te越高，效率越高。

3）优化后的膨胀机工况1下总-静效率ηc1.ts提高了1.23%，输出功率Wc1提高1.1%，轴向推力Fc1减小4.5%，工况2下总-静效率ηc2.ts提高1.44%，输出功率Wc2提高1.6%，轴向推力Fc2减小2.5%，工况3下总-静效率ηc3.ts和输出功率Wc3基本持平，轴向推力Fc3减小3.4%，三种工况下质量流量变化m均小于1%，R1和R2动叶的最大应力S、叶顶最大径向位移A，均满足材料力学性能和工程实际要求。

4）对设计变量分布情况做了分析，在R1动叶下半部正弯20°和40°时，高效点较为聚集，R2动叶下半部反弯-10°左右，上半部正弯45°时高效点比较集中；R1和R2动叶均在叶片下半部正弯20°～40°时，最大等效应力较大。

5）分析优化后的两级动叶片前六阶固有频率和振型图，对工作转速频率激励和静叶通过频率激励进行了评估，结果均合格。