W 波段UAV MISAR 实时成像运动补偿方法
曾朝阳,王 辉
(上海航天技术研究院毫米波成像技术重点实验室,上海 201109)
0 引言
毫米波具有频率高、波长短的特点,能够得到更高分辨率的合成孔径雷达(Synthetic Aperture Radar,SAR)图像,同时电磁散射细节特征丰富。近年来,毫米波SAR 成为了现代雷达发展的重要趋势[1]。W 波段与SAR 技术及调频连续波(Frequen⁃cy Modulated Continuous Wave,FMCW)技术的结合,促使了轻质量、低成本、低功耗的高分辨成像雷达的诞生,使其能够安装在小型无人机上,甚至在航模飞机上。FMCW 体制SAR 可以在接收端采用Dechirp 接收体制,回波信号与参考信号进行Dechirp,产生了较小带宽的差拍信号,从而降低对后端接收通道、后端A/D 采集设备和信号预处理设备的要求[2]。常规的脉冲式体制SAR,峰值发射功率较高,作用距离较远,但是整个SAR 系统质量大、功耗高、造价成本高,且对发射系统、馈线系统要求会比较高。同时整个系统对搭载平台也有很高要求,只能搭载于较大型运输机。FMCW 体制SAR因为发射脉宽大,只需要较低的峰值功率,用较低功率的固态放大器就可以满足系统要求,因此,系统造价会大大降低。而低成本的特点也促进了其在军民两用方面有更广阔的市场。总之,FMCW体制SAR 有着诸多的优点,国内外高校、科研机构对其研究也将越来越深入和广泛。
FMCW 体制SAR 与传统的脉冲式SAR 在成像处理方法上是不同的。传统的脉冲体制SAR 基于“stop-and-go”模型,即认为雷达是“一步一停”的工作模式。这是由于发射信号的脉冲宽度是微秒级,在信号发射过程中假设目标与雷达平台的相对距离没有发生变化,而FMCW 体制SAR 工作时发射天线一直在发射脉冲,扫频时间是毫秒级,扫频时间较长不能忽略,因此,在发射信号的过程中目标与雷达平台之间的距离是不断变化的。雷达平台的连续运动会使距离向产生多普勒频移,这个多普勒频移会使目标的回波包络产生方位向和距离向耦合,影响图像的聚焦[2-3]。
W 波段无人机载频高、带宽大,可以获得高分辨率SAR 图像。但由于W 波段波长约为X 波段1/10,对运动误差的敏感度非常高,同时无人机抗干扰能力差,平台运动误差进一步加大了获取W 波段高分辨率图像的难度。因此,准确的运动误差估计与补偿是W 获取波段高分辨率图像的难点。此外,由于要在实时系统上实现,因此,无法进行插值类操作,使得误差估计与补偿更加困难[4]。
针对上述问题,本文提出了一种基于惯导补偿和相位梯度自聚焦(Phase Gradient Autofocus,PGA)运动误差估计的中心波束平面补偿方法。该算法将惯导补偿与PGA 有机结合,利用惯导数据把带有运动误差的回波包络拉直,再利用PGA 算法对回波进行相位误差估计并补偿。相对于传统成像方法,该方法取消了徙动校正步骤,无需插值类操作,同时结合方位向子孔径数据处理方法,相对于传统的成像方法减少了每次快速傅里叶变换(Fast Fourier Transform,FFT)运算的数据长度,降低了在实时系统中实现时矩阵转置的难度,为后续实时成像的实现提供了可能。最后,通过点目标仿真验证了本模型的正确性和算法的有效性。
1 条带模式下FMCW SAR 回波模型
在脉冲SAR 信号处理中,因雷达发射的脉冲信号持续的时间非常短,一般为几个μs,而脉冲的调制周期为ms,即发射脉冲信号占用的时间非常少,调制周期内其余时间都用来接收回波信号。因此,相对于回波的延时,发射脉冲的时间是可以忽略的,目标与雷达之间的距离可以视为保持不变,这就是说相当于直接接收到目标的反射回波,不需要考虑SAR 沿方位向连续运动的影响。所以在传统的脉冲SAR 体制中,通常将雷达的连续运动等效为“停-走-停”(stop-go-stop),同一脉冲在收发的时刻,载机被视为是不动的。这种假设在脉冲SAR中广泛被应用。但是FMCW 体制SAR 发射的却是在整个调频周期内一直持续的连续波信号,发射信号和接收信号同时进行。由于载机的连续运动产生的瞬时斜距的不断变化在FMCW 体制SAR中不能被忽略,传统的脉冲SAR 的“停-走-停”模式在FMCW体制SAR中并不适用。因此,需要对FMCW 体制SAR 的回波模型进行分析。
1.1 瞬时斜距
图1为SAR 信号的条带正侧视成像几何关系,雷达载机飞行速度为v,载机的飞行高度为H,设点目标T(X0,Y0,Z0)到雷达的最近距离PcG为RB=则以离雷达最近点处为时间零点,在时间零点附近变化时,雷达与点目标的瞬时距离表达式为
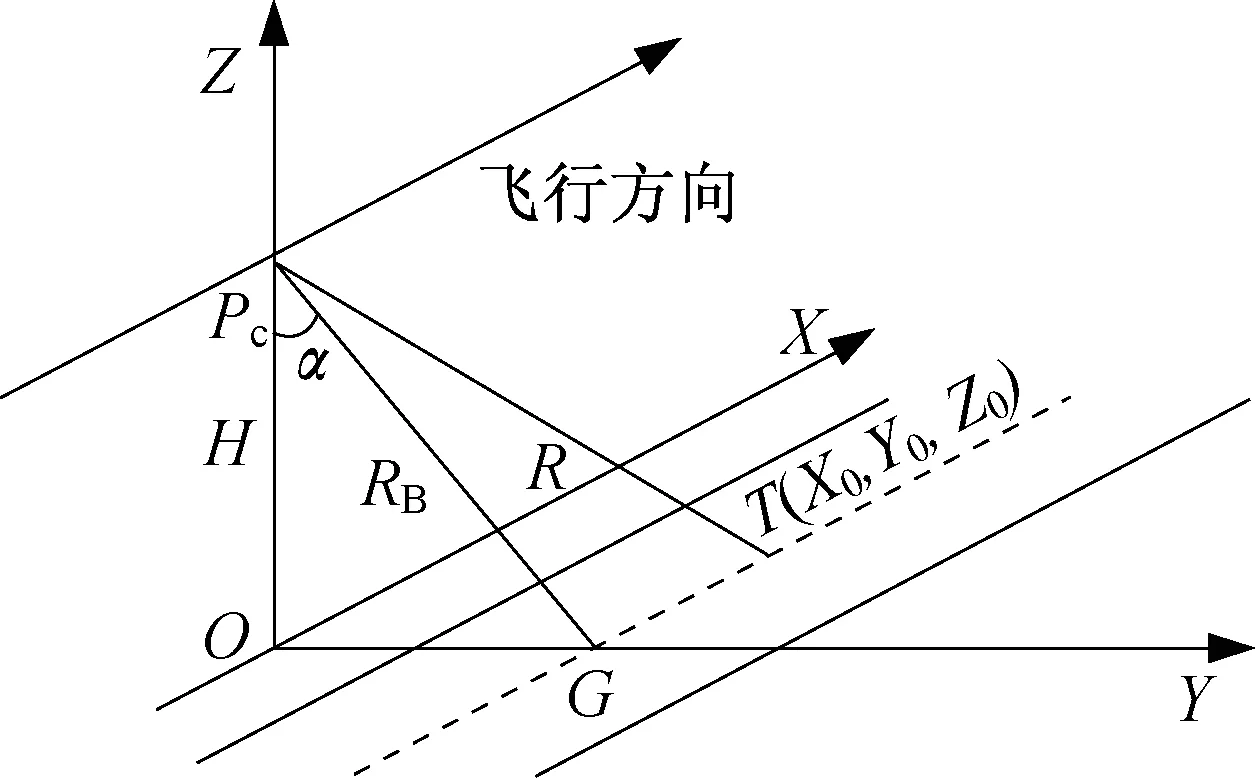
图1 条带SAR 成像几何关系Fig.1 Geometric relationship of strip SAR imaging
如图2 所示,锯齿波为调频连续波发射信号与接收信号。
由于发射机在整个发射周期内都发射电磁波,则某个时间点可以表示为

图2 FMCW 发射信号与接收信号Fig.2 Transmitting and receiving signals of FMCW

式中:tm=NTp,称为距离向慢时间变量,N为发射连续波整数个数,Tp为脉冲重复周期;t'为方位向快时间变量。
设雷达的相位中心的坐标为(x0,0,0),则雷达的瞬时斜距R(t',tm)表达式为

1.2 回波模型
本项目采用的连续波信号为锯齿波(见图2),FMCW 信号在一个周期的调制相位φ(t)为

式中:fc为发射信号载频;kr为发射信号调频率。
在整个扫频周期内,发射信号st(t)的瞬时表达式为

雷达系统接收到的回波信号sr(t)是发射信号的延时,即

将发射信号st(t)与接收信号sr(t)进行差拍,这样就得到去调频后中频信号sif,即

将t=t'+tm带入发射信号表达式中,发射信号的表达式为

则接收回波信号是发射信号的延时,延时时间为τ,表达式为

在实际的雷达接收系统中,调频连续波的去调频处理通常是将接收到的回波信号与最小距离参考点的参考信号相乘,去调频处理的参考信号表达式为

式中:Rref为参考距离。
去调频后的回波表达式为

2 实时成像处理算法
2.1 运动误差补偿方法研究
由SAR 基本原理和成像算法可知,载机的运动形成长的线性合成阵列,从而获得方位向的高分辨率。在理论分析时,载机的运动状况被假设为理想的,即雷达在空中沿着固定的航向和高度匀速直线飞行。实际情况下,载机的运动不可能是匀速直线飞行。受到天气等因素影响,载机的运动有很大的不稳定性。如果不采取运动补偿,则录取到的回波数据会有较大的失真,从而使成像质量下降,甚至不能成像。机载SAR 的运动补偿主要有两种方法:1)基于惯导数据的运动误差补偿;2)基于回波数据的运动误差补偿方法[6]。两种方法各有优点和不足:惯导系统是与雷达相分离的测量系统,其测量精度决定了补偿精度,因此,要想达到高分辨率效果,则必须配备高精度的昂贵的惯导设备[7-9];而基于回波数据的运动误差补偿方法是从雷达回波中估计相位误差,不受设备因素影响,但补偿算法相对复杂[5]。在进行运动误差补偿时,由于要在实时系统上实现,因此,无法进行差值类操作,采用中心波束平面补偿是一种有效的补偿方法。中心波束平面补偿指的是在每个回波录取位置,补偿中心波束平面上的点目标的运动误差,包括包络补偿与相位补偿。本文采用基于惯导的运动补偿与基于回波数据的PGA 运动误差估计方法相结合的中心波束平面运动补偿方法,既减少了系统成本,又降低了算法的复杂度,有利于实时成像算法在机载系统中的实现。
由载机受到干扰不平稳运动而引起的航迹误差如图3 所示。图3中,实线表示机载雷达的天线相位中心(APC)的实际航迹,而用虚线拟合出一条与实际航线最接近的直线,并认为载机雷达的APC沿该直线做速度为V的匀速直线运动,我们称之为“理想航迹”。以理想航线的起始天线相位中心位置为原点,以理想航迹飞行方向为X轴,Z轴与地面垂直,Y轴垂直于XOZ平面。为了便于分析机载雷达APC 位置误差各个分量的影响,可用[X(tm),Y(tm),Z(tm)]表示载机实际航迹,而“理想航迹”则表示为[Vtm,0,0],两种航迹的坐标差即雷达APC 位置的3 个误差分量。雷达APC 位置的自变量为方位向慢时间tm,因为雷达以一定的周期Tr重复工作,tm以Tr的整数倍离散变化,对于“理想航迹”,机载雷达APC 的位置也以等间隔(VTr)沿X轴均匀排列,而实际航迹与理想航迹相比较,其误差分量为[X(tm)−Vtm,Y(tm),Z(tm)],其中Y(tm)、Z(tm)为tm时刻法平面里偏离原点的误差。气流扰动等干扰因素可使载机在方位向和距离向有亚米级到米级的随机位移,它的变化较快。同样的因素也会影响载机速度,使瞬时航速偏离平均值,这种变化比较慢。若对很长的数据作一次性的成像处理,在某一段时间里载机的飞行速度可能会偏离平均速度,则X轴向的APC 位置误差X(tm)−Vtm有时比较大,可达米级甚至更多。因此,分子孔径进行运动误差估计和补偿很有必要。
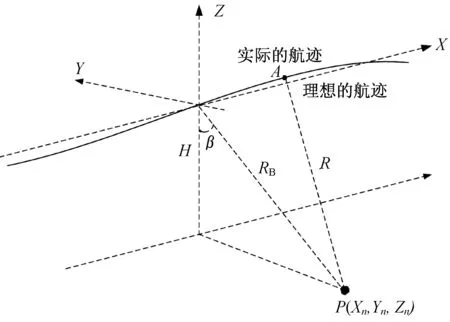
图3 存在运动误差的SAR 几何关系示意图Fig.3 Geometric diagram of SAR with motion errors
由惯导信息可以得到载机平台在地球空间坐标系中的东北天三向速度Veast、Vnorth、Vsky,机载XYZ三轴坐标系的飞行速度Vx、Vy、Vz。为便于分析,假设载机自西向东飞行。在地球空间坐标系下,载机的实际航迹位置[X1(tm),Y1(tm),Z1(tm)]为
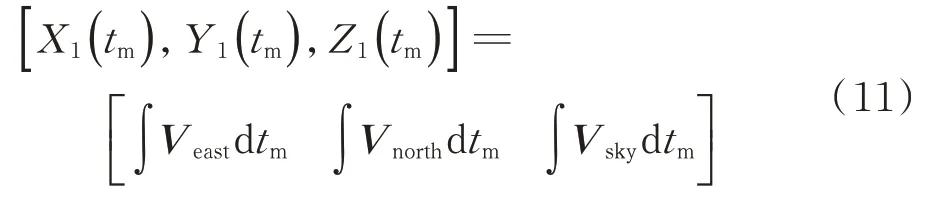
实际航迹与理想航迹的位置偏差ΔR1(tm)为
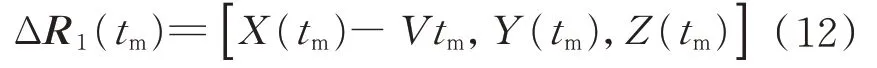
地球空间坐标系中的位置偏差转化到机载XYZ三轴坐标系中需要乘以一个旋转矩阵,即

式中:ΔR(tm)为机载XYZ三轴坐标系下实际航迹与理想航迹的位置偏差;θ为实际航迹与理想航迹在沿航迹方向的偏角。
故可得到利用惯导信息载机平台天线相位中心在中心波束平面内需要补偿的包络误差ΔR为

式中:MRotion为实际航迹与理想航迹位置偏差沿斜距投影到地面的投影矩阵。
进一步可得到载机平台天线相位中心在中心波束平面内需要补偿的相位Δϕ为

利用惯导数据对回波进行运动误差补偿后还有残余相位,继续使用PGA 对残余相位进行估计。PGA 算法直接对相位误差进行估计,能够同时补偿低阶和高阶的相位误差。PGA 算法包括4 个关键步骤:圆周位移、加窗、相位梯度估计和迭代运算。这4个步骤可以用不同的方法来实现[10-11]。
本文选择从复图像域出发,将散焦的图像聚焦。圆周位移和加窗针对图像域数据,相位梯度估计则需要通过IFFT(Inverse Fast Fourier Transform)到时域进行。
2.2 实时成像算法流程
实时成像由于受时间与内存等资源的限制,需要在满足成像精度的同时尽可能地降低计算复杂度,因此,在实现实时成像时应该尽可能地消除不必要的计算步骤。同时实时成像需要采用流水式设计,即对部分数据先进行处理,直到数据量达到全孔径时,进行方位脉压出图。对于更长时间的成像过程,先按照每两个全孔径数据进行成像处理各自出图,为了保证所有点都是全分辨,仅保留每幅图像中一个全孔径的图像大小,相邻两幅图像通过重叠一半进行图像拼接。这个时候,重叠部分的数据处理可以保留至于下一幅图像的成像过程中。
通过分析所设计系统的参数,减少实时算法的复杂度,系统参数见表1。

表1 实时成像系统参数Tab.1 Parameters of the real-time imaging system
由1.2 节回波模型知,Dechirp 接收信号需要去RVP 项处理,以消除剩余相位对方位聚焦的影响。针对Dechirp 接收信号,为了与成像算法更好地结合,设计采用Dechirp 转直采接收的处理方式。通过计算可得距离向8°的波束宽度对应的地面幅宽为222 m,斜距平面上为300 m。200 m 的幅宽与0.075 m 的距离向采样点数为2 666 点。考虑到波束宽度对应场景点数为4 000 点,因此,距离向成像点数最多只需用4 096 点。最优的方位分辨率为0.11 m×1.2=0.13 m。最大方位带宽小于300 Hz,考虑到900 的PRF,可以做一次方位数据抽取。全孔径数据点数在2 000 点以内。考虑方位抽取一倍,则只有1 000 点。
通过分析可知,所设计的系统由于波束宽度的限制,距离向最多只要4 096 点即可满足成像幅宽要求,方位向2 048 点可满足方位全分辨成像需求。同时距离徙动量小于一个距离单元,因此,可以忽略距离徙动的影响,从而取消距离徙动校正的步骤。所设计的实时成像算法流程图如图4 所示。

图4 实时成像算法流程图Fig.4 Flow chart of the real-time imaging algorithm
对录取的子孔径回波数据进行一次处理,首先通过RVP 项校正,去除因Dechirp 接收引起的方位相位调制,这一步骤可以对每一个录取的回波进行处理,不一定要累计到一定脉冲数量的子孔径回波数据。然后对距离向进行分块估计运动误差,这是因为由于观测距离较近,运动误差的距离空变不可忽略,需要通过多距离块的拟合实现运动误差的距离空变估计。每个子块的运动误差估计采用PGA的方式实现。当数据量累计到2 048 点时,这时方位数据已经达到两个全孔径长度,通过匹配滤波可以获得一个全孔径大小的全分辨图像,对数据进行运动误差补偿,并通过方位匹配滤波实现成像,最后做方位向多视出图。
2.3 几种实时成像算法的比较
在SAR 实时系统中,实现原始数据成像需要考虑算法实现时的运算量和存储量,同时还需要充分考虑到利用硬件电路进行计算时与普通计算机运算的差别。
对传统的距离多普勒(RD)算法、线频调变标(CS)算法,与本文论述的基于惯导和PGA 相位误差估计的中心波束平面补偿算法的运算量、存储量进行比较,见表2。

表2 实时成像算法的运算量及存储量对比Tab.2 Comparison of computation and storage of the real-time imaging algorithms
RD 算法和CS 算法都采用全孔径处理的方式,在实时成像系统中进行方位向运算时,通常取两个全孔径长度的数据进行运算,并通过重叠保留实现大面积的连续成像。采用中心波束平面进行成像时,方位向采用了子孔径的处理方法,缩短了每次进行运算的FFT 长度,在一定程度上能减小硬件的压力,并且两个全孔径重叠的部分不需要重新估计,重叠部分的数据处理可以保留至下一幅图像的成像过程中,极大地减少了运算量。
从算法的实时实现角度看,RD 算法运算量的大小以及成像质量的好坏主要取决于插值算法的精度,而在实时系统中,插值类操作很难实现。CS算法不需要插值,但在实时系统中实现时需要进行4 次全孔径数据长度的矩阵转置的操作,需要更多的处理板来实现转置功能。同时,CS 算法中各个补偿因子需采用泰勒级数展开等方法进行合理的近似以及补偿因子的三角函数运算的实现,都在一定程度上增加了软件开发的难度。本文提出的中心波束平面补偿算法优势在于不需要进行插值,同时矩阵转置的操作大部分都是小矩阵转置,大大降低了转置操作的难度。整体上看,虽然FFT 运算次数有所增多,但增加的都是短序列FFT,在基于FP⁃GA 的实时系统中实现具有很大优势。
3 仿真试验
为了验证本文分析的正确性,进行了点目标的仿真。系统仿真参数见表3。
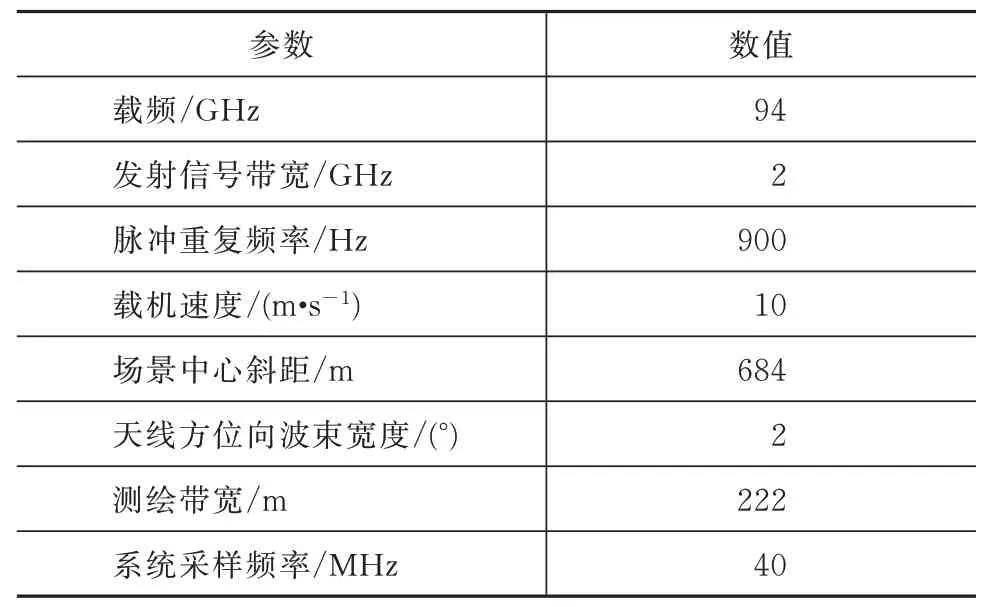
表3 仿真参数Tab.3 Simulation parameters
仿真XYZ三轴运动误差输入如图5 所示,仿真结果如图6 所示。

图5 XYZ 三轴运动误差仿真输入Fig.5 Simulation inputs of the motion errors of the X-,Yand Z-axes

图6 点目标二维成像结果Fig.6 Two-dimensional imaging result of the point target
成像结果方位向剖面如图7 所示。

图7 成像结果方位向剖面图Fig.7 Azimuth profiles of the imaging result
成像结果距离向剖面如图8 所示。点目标成像结果两维剖面分析见表4。可以发现,距离向的峰值旁瓣比和方位向峰值旁瓣比都接近理论值。绘图时采用了插值,使图像看起来更加平滑。

图8 成像结果距离向剖面图Fig.8 Range profiles of the imaging result
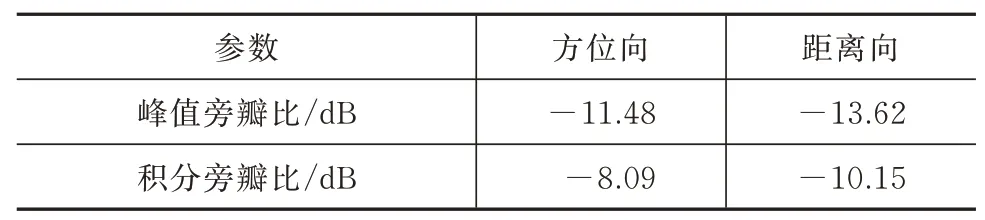
表4 点目标成像结果两维剖面分析Tab.4 Two-dimensional profile analysis of the point target imaging result
4 结束语
本文针对实时成像算法受限于时间与内存等资源的限制问题,提出了一种基于惯导的运动补偿与基于回波数据的PGA 运动误差估计方法相结合的中心波束平面运动补偿方法,完成包络校正和相位误差补偿。该方法在保证成像分辨率的前提下减少了成像算法的复杂度。仿真结果验证了该方法的有效性。

