再入过程中的同位素热源可靠性评估
吴胜娜,罗洪义,武伟名,李 鑫,唐 显
(中国原子能科学研究院 同位素研究所,北京 102413)
放射性同位素热源(RHU)是利用放射性同位素衰变产生的衰变热为探测器提供热能的装置。迄今为止,美国已在其多次航天任务中部署了百余枚RHU,其中先驱者号、旅行者号上装配的RHU,使用寿命均超过30年,长寿命、高可靠等特点使得RHU成为目前深空探测任务中能量供应的首选。RHU在执行任务期内可能经历各种复杂、恶劣的环境,包括再入大气层坠入深海等过程,任务要求RHU在经历上述环境条件下仍具备保持放射性物质不泄漏的能力。一方面,由于目前国内RHU的工程应用主要依赖于进口,无可借鉴的历史经验信息,因此无法通过相似产品法[1-3]进行可靠性评估;另一方面,单纯通过试验方法获得评估结果[4-9],所需试验规模大、测量精度难以保证。因此探索一套科学、实用的RHU可靠性评估方法,对RHU国产化应用具有十分重要的意义。基于此,本文以某型RHU为例,拟采用有限元仿真与试验相结合的方式,通过开展少量的研制试验并收集试验信息,对仿真模型进行反复修正,利用修正后的模型开展大量的仿真模拟试验,利用仿真模拟试验数据计算RHU的可靠度,以期在有限试验规模的前提下,获得满足用户精度要求的RHU可靠性定量评估结果。
1 RHU可靠性评估
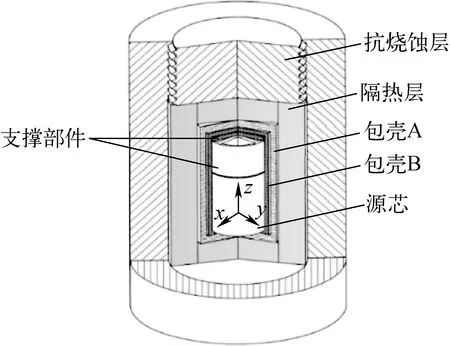
图1 RHU基本结构示意图[10]Fig.1 Structure of RHU[10]
RHU的基本结构示于图1。RHU由热源盒、隔热层、包壳B、包壳A、源芯及支撑部件组成。源芯是由放射性同位素原料制成的陶瓷芯块,其功能是产生热量,只要不发生散落,其功能就能满足;包壳A和B由特殊的金属合金制成,起密封放射性物质和力学保护作用,是衡量RHU可靠性水平的关键部件;隔热层的作用是在短时间内阻止热量大量传入包壳A、B,确保金属包壳的密封性;热源盒具有耐高温、抗烧蚀作用。
1.1 系统可靠性评估
RHU可靠性评估属于系统可靠性评估范畴,在系统可靠性问题的探究中,关于零部件失效之间的统计相关性、复杂载荷环境问题、复杂失效状态问题已开展了大量研究[11-12],但上述研究主要考虑载荷的复杂性,未能全面反映载荷的随机不确定性,本研究充分考虑载荷历程、工作环境分散性的影响,采用蒙特卡罗法,通过大量随机抽样得到RHU可靠性评估结果。
RHU再入过程可靠性是指RHU在再入大气层返回至深海过程中持续保证放射性物质密封的能力。首先采用解析法建立系统可靠性功能框图,结合失效模式分析,明确RHU的系统可靠性框图是包壳A和B的并联模型;而意外再入过程依次经历模拟空气动力学过热→热冲击→深海外压3个阶段,此过程为串联过程,因此,RHU在意外再入过程中的可靠性模型为串并联模型,如图2所示。

图2 RHU再入过程的可靠性框图Fig.2 Reliability block diagram of RHU in reentry process
其可靠度R的表达式如下:
R=[1-(1-R空气动力学过热,包壳A)·
(1-R空气动力学过热,包壳B)]·[1-(1-R热冲击,包壳A)·
(1-R热冲击,包壳B)]·[1-(1-R外压,包壳A)·
(1-R外压,包壳B)]
(1)
利用RHU零部件的可靠度分布函数,结合上述公式,采用蒙特卡罗法,即可得到RHU系统可靠度。
1.2 零部件可靠性评估
衡量RHU可靠性水平的关键部件包壳A和B,是由特殊的金属合金制成的,因此RHU零部件的可靠性评估属于结构可靠性评估范畴。目前已对船舶、采煤机等产品中的结构件开展了广泛的研究[13-16]。本研究采用机械产品可靠性评估方法中广泛使用的应力-强度干涉理论确定RHU中关键部件的可靠度。机械产品的可靠度为:
R=P{δ-S>0}
(2)
其中:δ为强度;S为应力。在实际分析中应力和强度的意义都可扩展使用。应力可泛指结构所受的外界载荷,如温度、冲击、振动等,强度则对应结构自身对外界载荷的承受能力,如温度阈值、模态频率等。
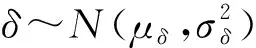

R=Φ(ZR)
(3)

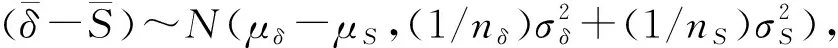
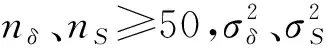
(4)
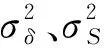
(5)

R=Φ(ZR)=
(6)
或
R=Φ(ZR)=
(7)
式(6)和(7)即为所求单元的结构可靠度分布函数。
1.3 RHU系统可靠性评估总方案
基于上述研究得到RHU系统可靠性评估的总体方案,如图3所示。首先根据3σ原则确定各试验条件的分布函数,同时利用ANSYS 有限元分析软件得到各零部件在不同环境载荷下的最大应力,然后基于各试验条件的分布函数,对有限元分析输入的试验条件进行参数化,采用响应面法进行试验设计,得到各零部件在不同环境载荷下的1组样本值,进而拟合出各组最大应力的分布函数,通过应力-强度干涉模型和信仰推断,得到各零部件在不同环境载荷下的可靠度分布函数,最后结合RHU的系统可靠性模型,通过蒙特卡罗仿真,在给定置信水平的前提下,得到RHU在意外再入过程中的系统可靠度置信下限。

图3 再入过程中RHU系统可靠性评估方案Fig.3 Reliability evaluation scheme of RHU in reentry process
2 RHU包壳结构可靠性评估
RHU在意外再入过程中依次经历模拟空气动力学过热→热冲击→外压3个阶段,各阶段具体试验条件如下。
模拟空气动力学过热试验条件:RHU表面温度(1 650 ±25) ℃,持续时间10 min。
热冲击试验条件:RHU表面温度(1 100 ±25) ℃,保持30 min,之后浸入温度为30 ℃水中。
外压试验条件:给RHU施加(100±5) MPa压力,保持10 min。
2.1 试验条件分布确定
RHU在意外再入过程中经历的3个阶段的试验条件并不固定,而是以某一分布形式表示,正态分布是一种常见的分布形式,本文以试验条件在给定容差范围内的概率为99.73%为准则,获得各试验条件参数的分布函数。
假设某一试验条件参数为随机变量X~N(μ,σ2),以目标值T为均值μ,代入容差c,即可按式(8)得到X的分布:
P(|X-T|≤c)=99.73%
(8)
根据上述方法分别求得各试验条件参数的分布如下。
模拟空气动力学过热试验条件参数分布:表面温度X~N(1 650,11.608 92),单位℃;持续时间10 min。
热冲击试验条件参数分布:热冲击试验计算分2个阶段,首先计算出金属包壳温度随时间的变化曲线,再基于温度随时间的变化速率得到热应力。而表面温度随时间变化的数据量较大,无法进行参数化,基于均匀设计的思想,选取1 075、1 100、1 125 ℃ 3个温度点进行热应力计算。
外压试验条件参数分布:施加压力X~N(100,2.262),单位MPa;保持10 min。
2.2 最大应力分布
从RHU的故障模式及影响分析(FMEA)出发,综合考虑可收集到的可靠性数据类型和样本量大小,基于产品在不同任务剖面下的材料性能数据,以及研制试验和鉴定试验过程中收集到的信息,对仿真模型进行反复修正,计算各试验条件下金属包壳的最大应力分布。
以空气动力学过热试验为例,试验条件的输入参数为1 650 ℃,利用瞬态热分析,得到RHU 2层金属包壳的温度分布,如图4所示,其中,包壳A的最高温度为1 667 ℃,包壳B的最高温度为1 661 ℃。
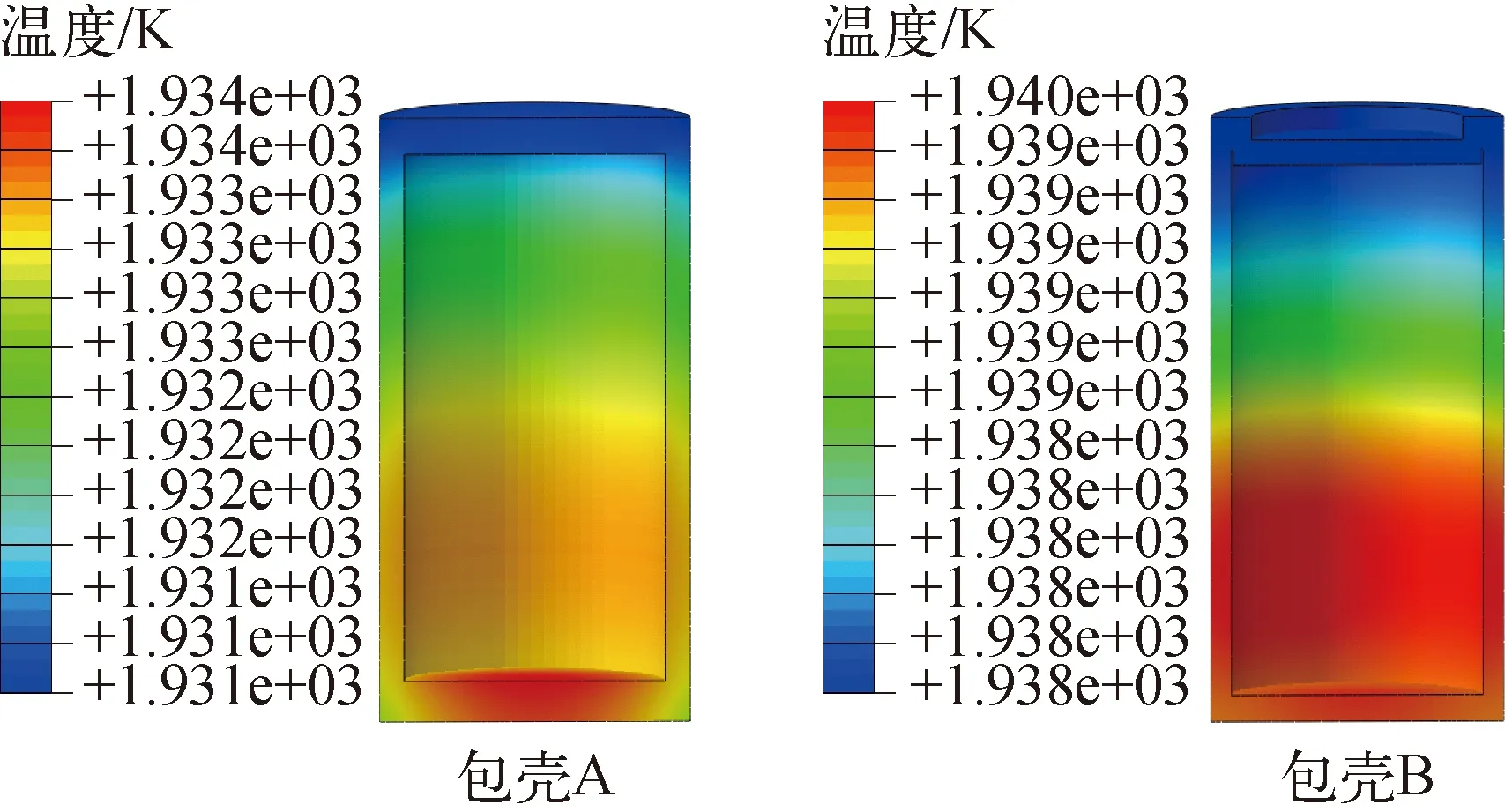
图4 1 650 ℃空气动力学过热下金属包壳温度分布Fig.4 Temperature distribution isopleth of metal cladding under condition of aerodynamic overheating at 1 650 ℃
将输入条件中的表面温度参数化为X~N(1 650,11.608 92),采用响应面法(SSA)进行试验设计,得到包壳A和包壳B最高温度的1组样本值,如表1所列。

表1 空气动力学过热试验条件下各层包壳最高温度Table 1 Maximum temperature of metal cladding under aerodynamic overheating test condition
对表1数据进行正态分布检验,得到在模拟空气动力学过热试验条件下,包壳B和包壳A最高温度的分布函数,分别为N(1 667.54,18.9322)和N(1 667.49,18.9312)。
上述计算结果表明,包壳A和包壳B最高温度的分布函数基本一致,故取1 667 ℃作为2层金属包壳的输入边界条件,根据克拉伯龙方程pV=nRT,将压强p、气体体积V、物质的量n(放射性源衰变公式计算得到2年后发射时产生衰变气体的物质的量)、绝对温度T以及气体常数R=8.314 Pa·m3/(mol·K)代入克拉伯龙方程,计算得到2年后发射的最大内压为11.3 MPa。,从而得到1 667 ℃下金属包壳2年后发射的应力分布云图,如图5所示。

图5 空气动力学过热试验2年后各层包壳内应力云图Fig.5 Internal stress isopleth in metal cladding after 2 years of aerodynamic overheating
将2层金属包壳最高温度和最大内压参数化,最高温度的分布函数取N(1 667,18.932),2年后发射的最大内压分布为N(11.3,0.112),由温度和最大内压共同作用得到的金属包壳最大等效应力样本值列于表2。

表2 空气动力学过热试验条件下各层包壳2年后的最大等效应力Table 2 Maximum equivalent stress of metal cladding after 2 years of aerodynamic overheating
对表2数据进行K-S检验,结果显示,包壳A、B的最大等效应力的p值均大于0.05,即所检验的样本满足正态分布。同时可得到,在模拟空气动力学过热试验条件下,两层金属包壳2年后最大等效应力的分布函数分别为N(44.62,0.6632)和N(21.33,0.3822)。
同理,可得到RHU在再入过程其他阶段包壳A和B的应力分布,如表3所列。

表3 再入过程各阶段金属包壳应力分布Table 3 Stress distribution of metal classing in each phase of reentry process
2.3 材料强度分布
根据包壳A、B在不同温度下的抗拉强度检测数据,选取正态分布函数类型进行拟合,分别得到包壳A、B在常温、1 100 ℃以及1 600 ℃条件下的抗拉强度的分布,如表4所列。

表4 RHU各试验条件下金属包壳强度分布Table 4 Strength distribution of metal cladding under test condition of RHU
2.4 可靠度分布
将RHU在再入过程各阶段的包壳A、B的应力分布(表3)及强度分布(表4)数据代入式(7),即可得到RHU零部件的结构可靠度分布。
3 RHU系统可靠性评估
利用MATLAB进行蒙特卡罗仿真(图6),仿真次数N=10 000,取α=0.05,计算得到RHU再入过程可靠度置信下限为0.999 989(置信度为95%)。
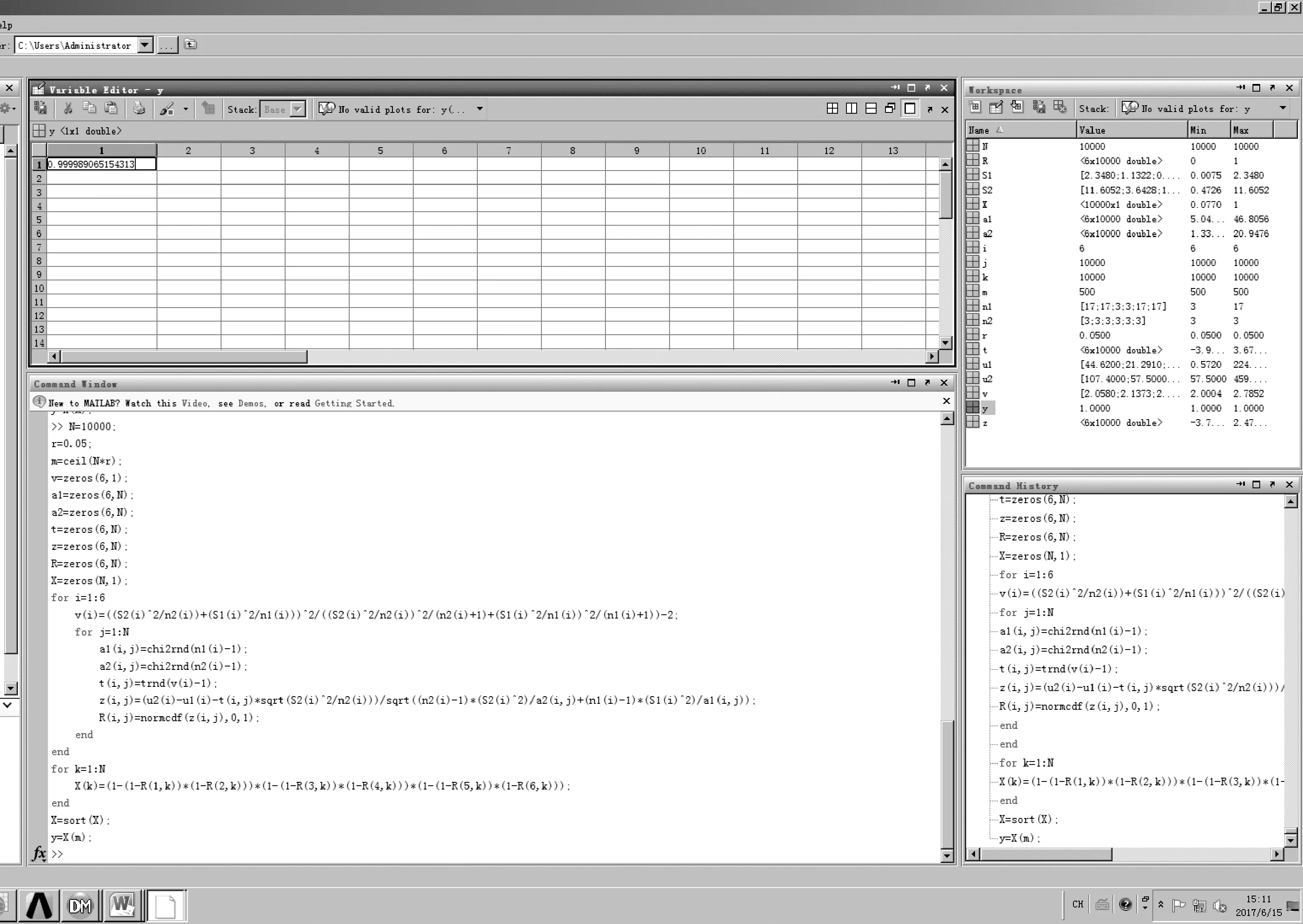
图6 系统可靠度置信下限蒙特卡罗仿真Fig.6 Monte Carlo simulation of system reliability low confidence limit
4 结论
1) 对于零部件结构可靠性评估,考虑应力和材料强度的不确定性因素,进行基于响应面法的随机有限元分析,分别得到了应力和强度的随机分布,根据应力-强度干涉理论,评估零部件的结构可靠度。
2) 对于系统可靠性评估,针对显式功能函数较为复杂的RHU系统可靠度评估,采用蒙特卡罗法结合解析法的综合法计算结构可靠度,显著提高了计算效率。
3) 基于小样本的可靠性评估问题,采用研制试验与仿真模拟试验相结合的方式,可根据用户评估精度要求,相应地调整仿真模拟试验样本量,对于试验规模有限的产品可靠性评估问题,具有十分重要的参考价值。

