一种改进的双馈风力发电网侧变流器控制策略

胡向前，毕雪芹，陈超波

（西安工业大学 电子信息工程学院，西安710021）

双馈风力发电机组作为风力发电的主要机型[1-2]，主要通过控制双馈风力发电机转子侧电流来实现并网电压的稳定输出，其系统结构如图1所示，网侧变流器（GSC）和转子侧变流器（RSC）协同合作完成对双馈发电机转子侧电流进行变流控制与并网。当电网发生不平衡故障时，主要通过GSC 来提前发现和处理电网不平衡波动，以降低电网不平衡对风力发电机的影响，因此在不平衡电网电压下，对网侧变流器控制策略具有较高的要求。

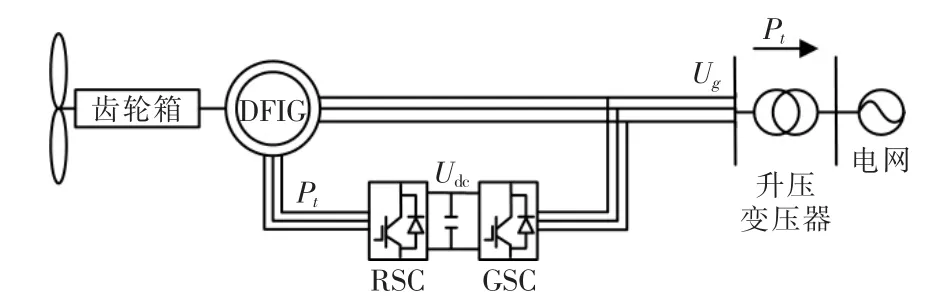
图1 双馈风力发电机组硬件结构图Fig.1 Hardware structure diagram of doubly-fed wind turbine

不平衡条件下，网侧变流器的控制策略主要通过在两相旋转坐标系下，三相交流电呈现直流特性[3]，通过双PI控制算法分别计算控制器对正、负序分量的给定参考值，实现对负序分量的抑制，但PI控制对交流信号抑制能力较弱，不能消除系统的交流误差，文献[4]通过设计数字陷波器的方法，精准分离出不平衡电网电流中正序分量，并计算谐波分量的补偿值，抵消了负序分量对系统的影响，文献[5-7]提出了网侧变流器直接功率控制，有效地降低了负序分量的影响，但需要查表确定PWM的参考电压，造成系统硬件参数难以确定，文献[8-9]通过在两相静止坐标系下，利用比例谐振控制器直接控制正序分量，避免了因正负序分解的时间延时，加快了系统响应速度，文献[10-11]提出来滑模变结构的直接功率控制策略，消除了因坐标变换造成的瞬时功率误差的影响，但需要进行正负序分解，增加了系统的复杂性。

本文通过建立基于LCL型并网变流器的数学模型，并通过坐标变换将数学模型换为两相静止坐标模型，在此基础上提出了基于比例积分谐振控制和滑模变结构控制策略：

（1）通过比例积分谐振控制器对网侧电流值谐波分量进行初步滤除；

（2）通过计算网侧变流器的输出有功功率和无功功率的参考值和实时值，并通过滑模变结构控制对系统进行功率控制，使系统产生稳定的网侧电流，从而消除了谐波和负序分量的影响。

1 网侧逆变器系统模型建立与分析

双馈风力发电机组因其转子电流幅值仅为定子电流的1/3，降低了对变流器容量的要求，背靠背变流器作为双馈电机转子电流并网的重要部件，由转子侧变流器（RSC）和网侧变流器（GSC）两个PWM变换器组成，直流母线电压间并联有大容量的滤波电容，在轻度不对称电压条件下可保证直流母线电压稳定不变，成为两变流器之间具备解耦运行的条件，因此可分别对两变流器进行控制器设计。

本文根据网侧变流器的主电路图建立数学模型，通过建立在αβ坐标系下的功率关系，通过比例积分谐振控制器对负序分量进行抗扰动控制，降低电网电压中负序分量带来的谐波扰动，对网侧变流器的有功、无功功率进行计算，采用滑模变结构控制算法进行功率精准控制，从而实现网侧变流器的控制策略在电网不平衡状态下，网侧变流器对负序分量进行完全抑制，提高系统对负序分量扰动响应的快速性和稳定性。

网侧变换器主电路如图2所示，根据基尔霍夫定律，建立三相电网电压不平衡情况下，在三相静止坐标系下网侧变流器的数学模型。

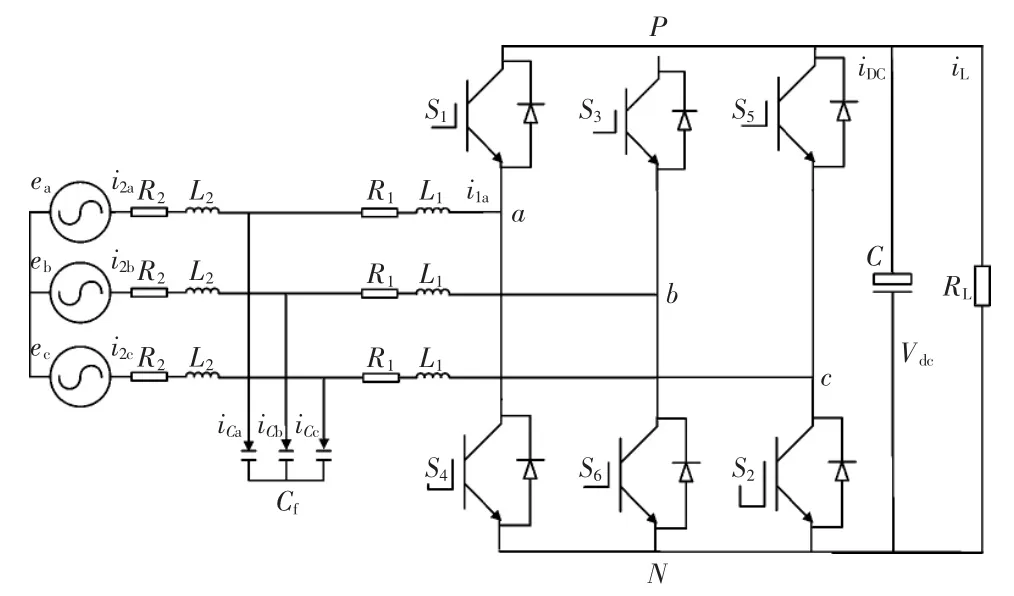
图2 网侧变流器主电路图Fig.2 Main circuit diagram of the grid side converter

由KVL、KCL定理求出网侧变流器电压电流关系如式（1）所示：

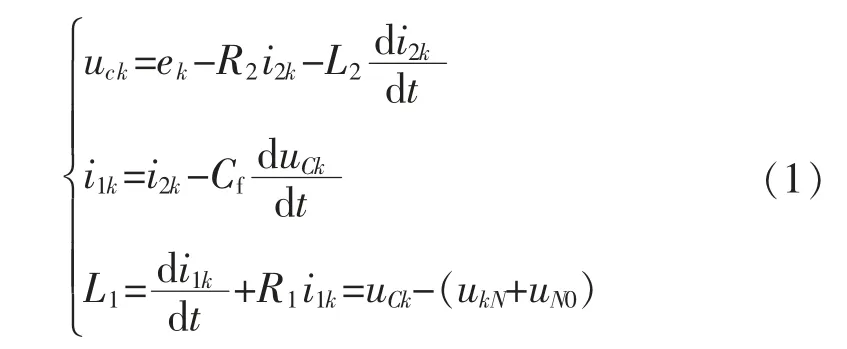
式中：uCk为滤波电容电压；ek为电网电动势；i1k为桥臂侧电流；i2k为电网侧电流；L1为桥臂侧电感；L2为网侧电感；Cf为滤波器电容。

根据逆变器电压与功率器件的关系，得到三相静止坐标系下网侧变流器的数学模型如式（2）所示：

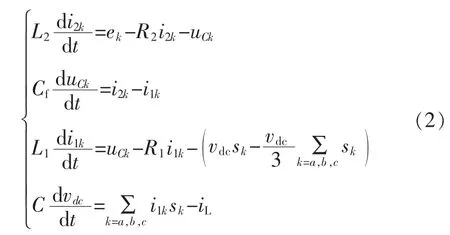
式中：C为直流侧电容；vdc为直流侧电压；sk为三相PWM变换器中各相桥臂的开关函数，开关函数如式（3）所示：

经恒幅值坐标变换得到网侧变流器在αβ坐标系下的关系如式（4）表示：

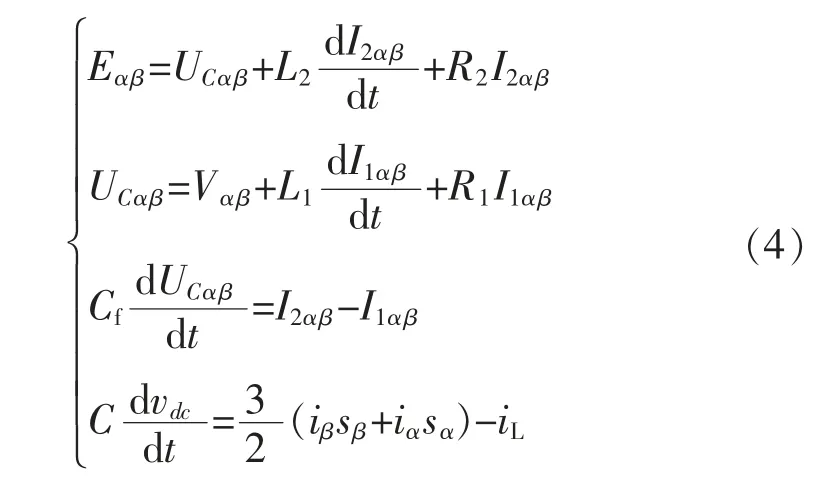
式中：Eαβ、UCαβ、Vαβ、Cf、I1αβ、I2αβ分别为网侧电压、电容电压、逆变侧输出电压、滤波电容、逆变侧输出电流、并网输出电流，网侧变流器的功率关系中网侧变流器的有功功率、无功功率表达式如式（5）所示：

若以d轴为电网电压矢量的两相静止坐标系的基准轴时，有功功率和无功功率表达式为

根据建立的数学模型关系，通过控制静止坐标系的电压电流，可实现对功率的精准控制。

2 控制算法的实现

2.1 PIR控制器的实现

比例积分谐振控制器是在原有PI控制器的基础上加入谐振控制器，用于提高控制器在指定谐振频率点的增益，比例积分谐振控制器的传递函数为式（7）：

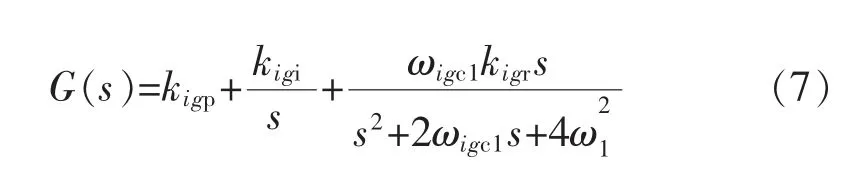
式中：kigp、kigi、kigr分别为网侧变换器PIR电流控制器的比例、积分和谐振系数，ωigc1为谐振电流的衰减系数，工程应用中ωigc1取值范围为5～15 rad/s，在Matlab 中建立控制器仿真，结果如图3所示，随着截止频率的不断增加可以发现，当电网频率发生波动的情况下，谐振调节器也能提供足够大的幅值增益，本文选择ωigc1为10 rad/s。

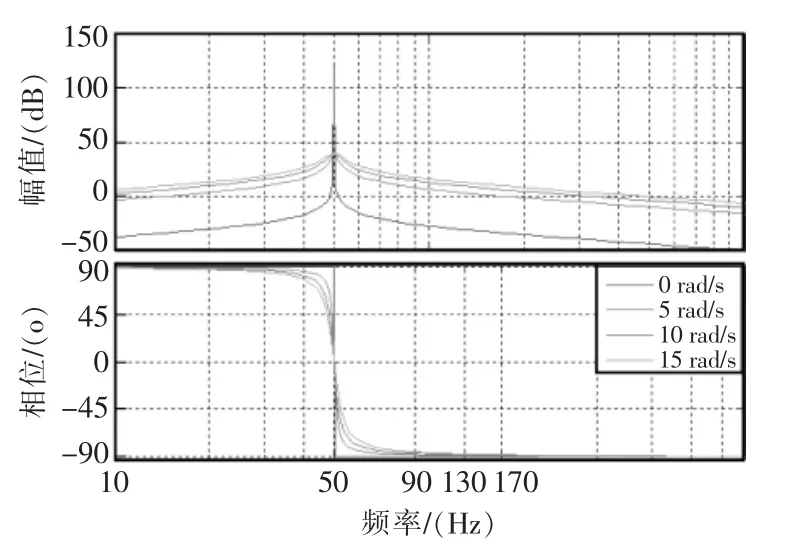
图3 PIR控制器伯德图Fig.3 PIR controller Bode diagram

网侧变流器矢量电压表达式如式（8）所示：

将上式变换得到网侧电压参考值的表达式如式（9）所示：

其中U′Cαβ表达式如式（10）所示：

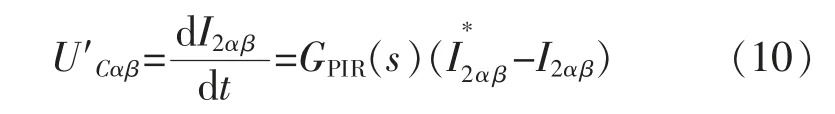
式中：GPIR（s）为PIR控制器的传递函数。

2.2 滑模变结构控制策略实现

滑模控制作为一种非线性控制方法，其基本思想是根据系统期望的动态特性设计滑动面的等效控制，使系统状态从超平面之外向滑动面转移，并根据滑动模态存在的条件使得系统平稳到达滑动面。

设不连续控制系统的微分方程为表达式（11），切换函数为表达式（12）：

式中：x＝[x1，x2，x3，…，xn]为n维状态向量；f=[f1，f2，f3，…，fn]T为已知n维向量函数；fl= fi（x，t）（i=1，2，3，…，n）为关于x的方程；u=[u1，u2，u3，…，um]T为m维不连续控制向量，其中u为各控制分量；S（x）=[S1（x），S2（x），S3（x），…，Sm（x）]为切换函数；B（x，t）为n×m 阶矩阵。

滑模变结构控制系统首先定义滑模面函数，通过判断滑模面函数的正负来控制系统状态变量的大小，使得系统状态快速运行到滑模面，并沿滑模面到达平衡零点。

滑动面函数S（x）=0时，系统到达滑动面，为研究滑动面的稳定性，需引入李亚普诺夫函数来判定，若李亚普诺夫函数表达式如式（13）所示：

且式（13）恒满足式（14）的要求：

则说明在理想条件下，当系统的状态进入滑动面后，系统将满足式（15）的条件：

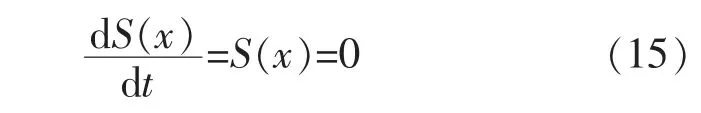
一旦系统脱离滑动面，系统状态将立即沿与滑动面相切方向运动并回到滑动面，使得系统在滑模面切换过程容易出现高频抖动现象，主要是因为切换函数为符号函数，在切换过程存在大的跳动，因此切换函数可选择饱和函数，使得系统平稳过度，降低系统的高频抖动。

在电网电压不平衡和电网电压畸变情况下，网侧变流器输出平均有功功率和无功功率与基波正序电网电压与正弦电流的关系如式（16）所示：

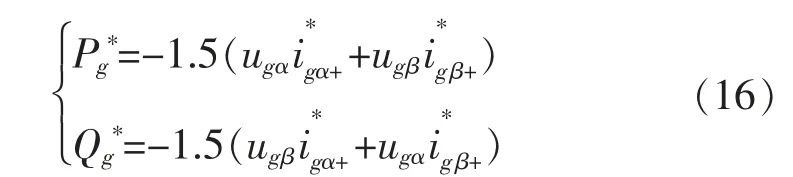
式中：pg*和Qg*分别为网侧变流器输出平均有功功率和平均无功功率给定，若控制器能对给定值进行精确跟踪，则网侧变流器输出电流为网侧电流的参考值，即消除了网侧变流器的负序分量及谐波分量。

若想对功率进行精确控制，需要控制有功功率实时值与给定值的误差为零，将滑模变结构与直接功率控制方法相结合，可消除系统的负序分量和谐波分量。

定义滑模变结构的滑模面函数如式（17）所示：

式中：S1、S2为有功、无功功率的滑模面函数；Pg*、Pg为有功功率指令值和实时值；Qg*、Qg为无功功率指令值和实时值，当系统稳定时，其滑模面函数的变化率为零，实时值与跟随指令值变化，从而消除负序分量对系统的影响。

控制的系统框图如图4所示，控制思路如下：首先通过电压外环计算得出交流电流参考值，并经坐标变换到两相静止坐标系中，计算出网侧电流信号的参考指令值，通过PIR控制器对网测电流进行消抖处理，然后计算网侧变流器的有功、无功功率指令值和瞬时值，经过滑模变结构控制策略，对网侧变流器的输出功率进行直接功率控制，最后输出SVPWM所需的参考电压值。

图4 PIR控制与滑模变结构控制结构Fig.4 PIR control and sliding mode variable structure control structure

3 仿真验证分析

为了验证上述分析，通过在Matlab/Simulink 搭建双馈风力发电网侧变流器控制模型，对2 MW 全功率网侧变流器在电网谐波畸变时的并网运行工况进行仿真研究，其中网侧变流器输出的电压有效值为690 V，电网频率为50 Hz，直流母线电压为1080 V，桥臂侧电感为0.075 mH，电网侧电感为0.035 mH，滤波电容为55.7 μF，功率器件的开关频率为2.5 kHz。

在Matlab 中搭建双馈风力发电网侧变流器的数学模型，首先对控制策略在电网无扰动情况下进行模拟仿真，得到理想条件下PIR控制策略和PIR加滑模控制策略下，网侧变流器电压输出波形如图5、图6所示。

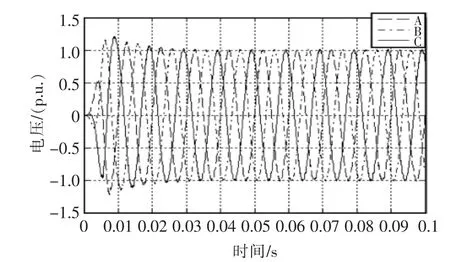
图5 理想条件下PIR控制策略输出Fig.5 PIR control strategy output under ideal conditions

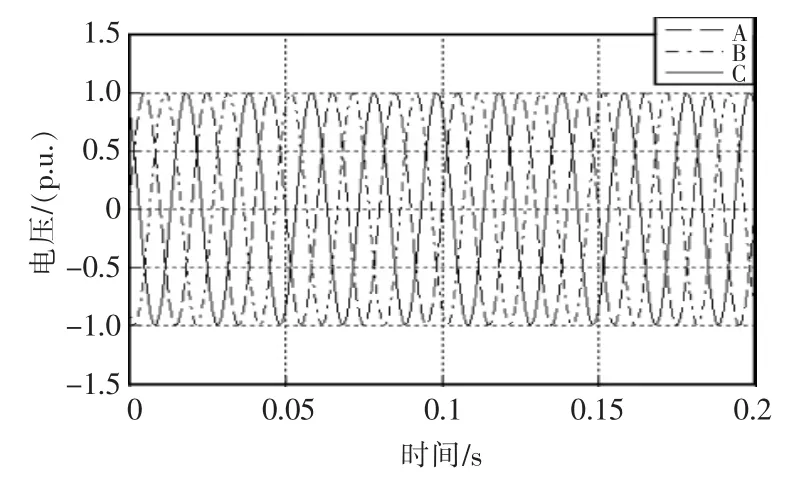
图6 理想条件下PIR与滑模控制输出Fig.6 PIR and sliding mode control output under ideal conditions

通过图5、图6展示的理想条件下网侧变流器输出电压输出波形可以看出，单纯PIR控制策略在系统启动过程中，系统响应速度较改进控制策略的速度慢，稳定之后通过Matlab 中Powergui 工具计算两个电压输出的谐波畸变率（THD）值分别为3.4%和2.3%。根据并网要求并网电压的谐波畸变率不能大于4%，两种控制策略均可实现并网要求，基于比例积分谐振和滑模变结构控制策略在稳态时输出更加稳定。

电网故障主要分为单相、两相、三相短路故障，当电网发生不平衡故障时，单相短路故障次数较多，本文仿真采用电网发生单相接地故障，对两种算法进行模拟仿真实验，结果如图7、图8所示。

图7为PIR控制在A相短路故障时输出的电压波形图，当发生单行短路故障时，C相电压发生畸变，幅值增大加据系统对输出的影响，图8为PIR控制与滑模变结构控制共同作用的电压波形，当A相发生短路故障时，B、C两相之间可以做到解耦控制，避免了因单相故障造成的二次危害。

图7 A相短路故障PIR控制输出Fig.7 A phase short circuit fault PIR control output

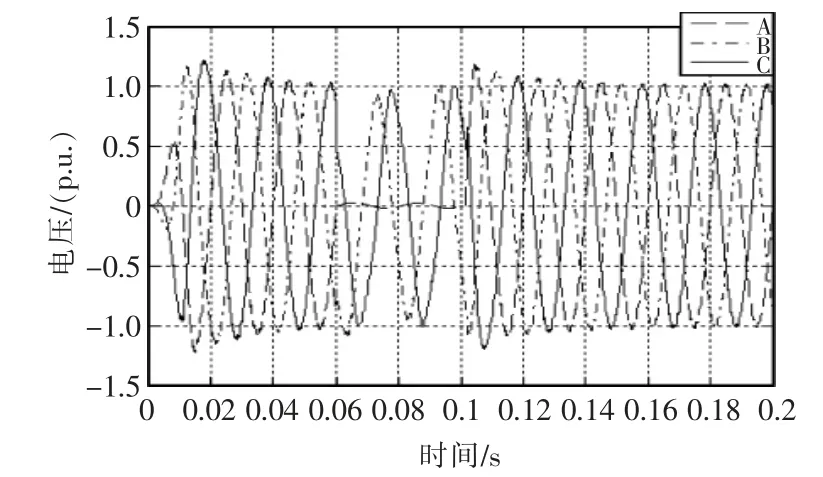
图8 A相短路故障PIR与滑模控制输出Fig.8 A-phase short-circuit fault PIR and sliding mode control output

4 结语

基于比例积分谐振控制和滑模变结构控制，可以通过两相旋转环坐标系直接对电网电流进行控制，避免了坐标变换和正负序分解，从而降低了系统的复杂性，提高了系统的响应速度，通过该策略实现单相短路故障时对负序分量的抑制和三相电路的解耦控制，提高了系统的抗干扰能力。