基于滑模控制的独立光伏发电系统控制策略

宋汶秦，薛 晟，张中丹，王兴贵，郭 群

（1.国网甘肃省电力公司 经济技术研究院，兰州730050；2.兰州理工大学 电气工程与信息工程学院，兰州730050）

随着能源需求的急剧加大和石化能源的不断消耗，其他可替代能源受到越来越多的关注，丰富的太阳能资源在应用中被证明是一种经济的能源[1]，目前光伏发电系统作为分布式电源受到人们的重视，为提高能源利用率，对光伏发电系统进行最大功率点跟踪（MPPT）成为其研究重点之一[2]，最大功率点跟踪是一个自动寻优过程，为克服固定电压法、电导增量法、扰动观察法[3]等常用MPPT 方法的缺点，近年来发展了滑模控制、模糊逻辑控制、遗传算法等智能控制方法，以提高控制精度和响应时间[4]。

对于离网运行分布式发电系统，可以采用蓄电池等储能装置，其对于系统的稳定控制、电能质量改善和不间断供电具有非常重要的作用，文献[5]介绍了多种适用于独立发电系统的储能装置；文献[6]比较了不同储能装置的特点，文献[7]提出孤岛微源逆变器双闭环控制策略，实现对交流母线电压和频率的稳定控制；文献[8]在传统下垂控制的电压电流环加入动态虚拟阻抗反馈，增强了系统频率和电压的动态稳定性。在此，以研究光伏电池滑模MPPT控制为基础，分别提出了逆变器输入侧直流母线电压稳定控制策略和独立光伏发电系统微源逆变器电压电流双闭环控制策略。

1 系统拓扑结构及数学模型

所研究的独立光伏发电系统拓扑结构如图1所示。光伏电池PV（photo voltaic）组件输出后，经第1级Boost变换器实现升压，以满足负载侧直流母线电压利用率要求[9]，同时实现光伏阵列MPPT；第2级电路由三相逆变器，通过滤波器连接到负载组成。逆变器输入侧直流母线通过双向DC/DC变流器接入蓄电池，确保系统输出电压稳定，以满足负载供电需求。

图1 系统拓扑结构Fig.1 System topology

1.1 光伏阵列模型

理想的单个光伏电池可等效为电流源并联二极管的形式，考虑光伏阵列形式，其I-U 特性表示为[10]

式中：Ipv为输出电流；Upv为输出电压；Isc为光生电流；I0为二极管反向饱和漏电流；Uth为光伏阵列端电压；Rs为光伏阵列的等效串联电阻；Rb为等效并联电阻。

1.2 boost变换器模型

通过VT7开关函数u的模式组合，得到Boost变换器的状态空间平均模型如下：

u=0时，VT7关断，二极管VD1导通，电感L放电，电容C充电，表达为

u=1时，VT7导通，VD1截止，电感L 储能，电容C 放电，表示为

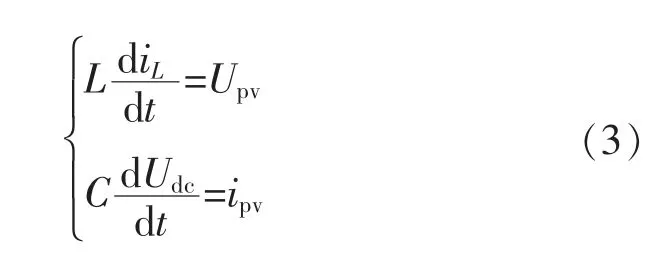
式（2）、式（3）平均得到变换器的平均状态空间模型为

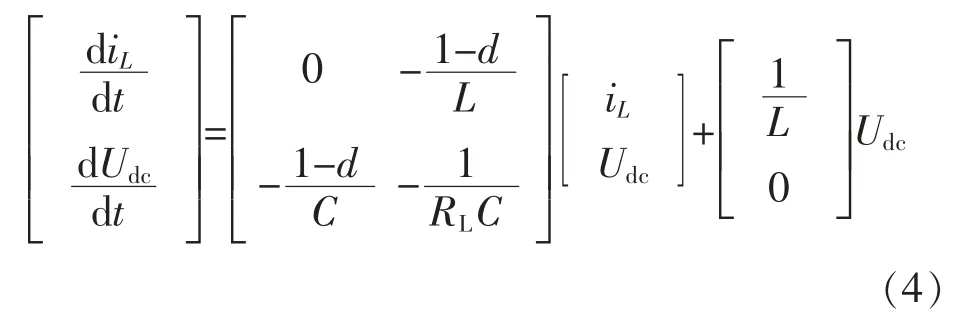
式中：RL为Boost输出直流侧等效负载；d为VT7占空比。

1.3 逆变器模型

逆变器采用滞环电流控制策略，其输出电压va，vb，vc以及直流侧输入电流Idc与逆变器开关状态s1，s2和s3有关。

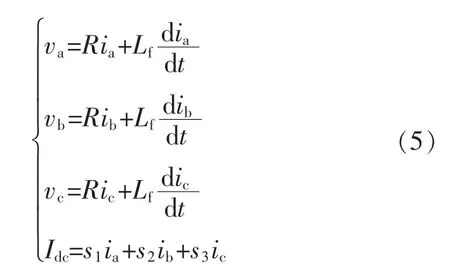
1.4 储能系统模型

双向DC/DC变流器的上、下桥臂开关管控制信号反向，两管交替互补导通，这种控制方式不需要状态逻辑单元就可以获得双向状态切换，系统响应更快[11]，忽略开关损耗，可得系统状态空间方程为

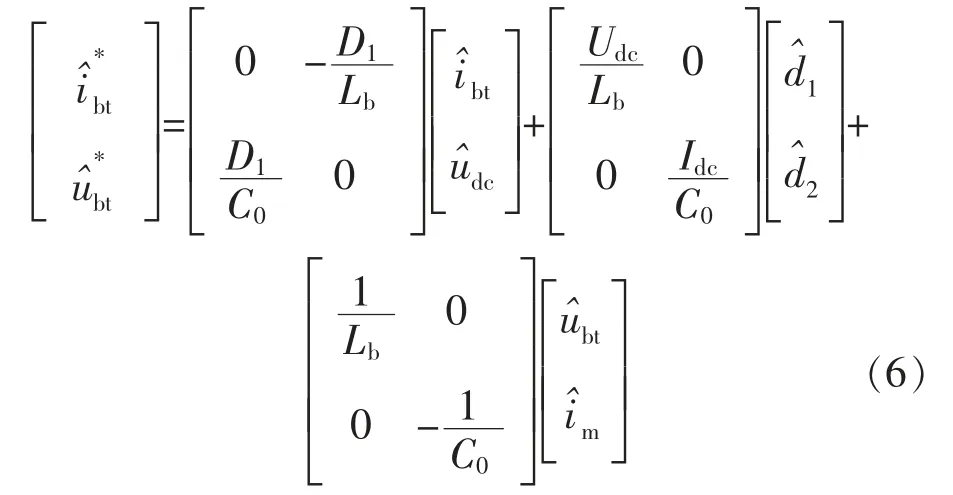
式中：d1，d2分别为双向DC/DC变流器开关管V1，V2的占空比；im为储能系统输出电流；Ibt为蓄电池输出电流；ubt为蓄电池端口电压。

2 系统控制策略

2.1 光伏电池滑模MPPT控制

滑模控制应用于微源MPPT 具有良好的跟踪性能且抗干扰性强，在此采用一阶滑模控制器作为优化工具，由PV 特性曲线可知，当∂Ppv/∂Upv=0，即Upv∂Ppv/∂Upv+Ipv=0时，太阳电池将持续产生最大功率输出，因此定义滑模切换函数s，可得

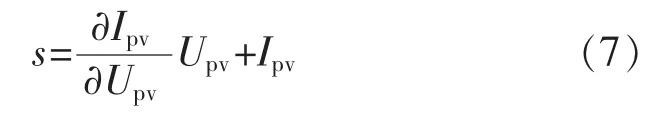
而在PV输出功率曲线中，滑模切换函数s 叠加调节量Δ 即可到达MPP点。因此可将控制函数α设置为

为减少系统不确定性及外界干扰对系统的影响，将滑模控制结构分为等效控制αeq和变结构控制αw两部分，即

其中，αeq确保系统状态在滑模面上，αw确保在非理想情况，系统状态不离开滑模面，αeq由条件s˙=0 得出，满足：

变结构控制αw可定义为

式中：K为趋近律系数，且K>0。存在边界层Δ，使得sat（s）满足：

因此，控制信号α应为

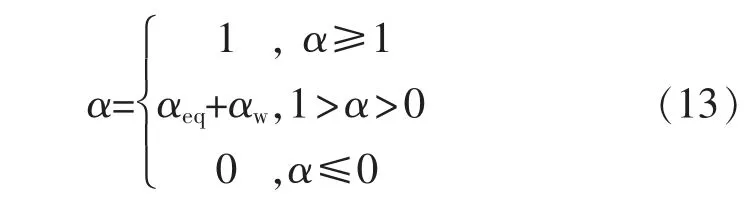
结合文献[12-13]可知，选取李亚普洛夫函数为

在此所选滑模切换函数s满足广义滑动模态存在条件，即

则对于系统（4），选择切换函数（7），采用式（13）所示开关信号，系统存在滑动模态，并符合稳定性需求。

2.2 逆变器输出控制

独立光伏发电系统运行时，为确保系统能够稳定运行，逆变环节采用电压电流双闭环控制，从而为系统提供电压和频率支撑，电压外环的主要作用是确定指令电流的参考值和稳定系统逆变器交流侧电压幅值，电流内环根据指令电流参考值对电流进行控制，实现电流快速跟踪。系统控制原理如图2所示。

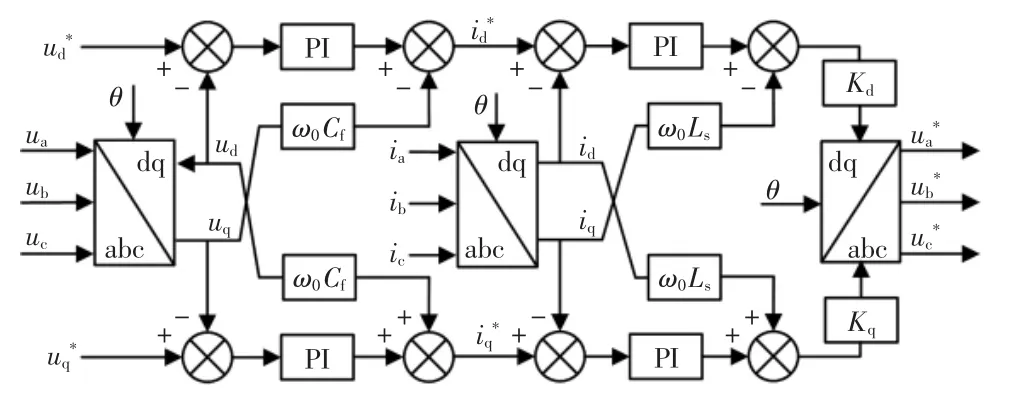
图2 逆变器输出控制原理Fig.2 Inverter output control schematic

系统运行时，坐标变换相位θ 由系统给定频率积分所得，电压外环的给定电压与反馈电压作比较后，经PI 调节器并加入滤波电容电流解耦分量得到电流内环参考值，之后与反馈电流进行比较，电流环也采用PI 调节器，输出后加入电感电压解耦分量得到电流内环输出量，再乘以调节系数Kd，Kq并经坐标反变换得到系统调制信号参考值。

2.3 储能系统控制

蓄电池双向DC/DC变流器工作于单端稳压模式以确保逆变器输入侧直流母线电压稳定，母线电压参考值Udc*与测量值Udc的差值经PI 调节器得到蓄电池参考电流ibt*，与ibt作差经PI 调节器得到输出控制信号，经脉宽调制后实现变换器的控制。其控制原理如图3所示。

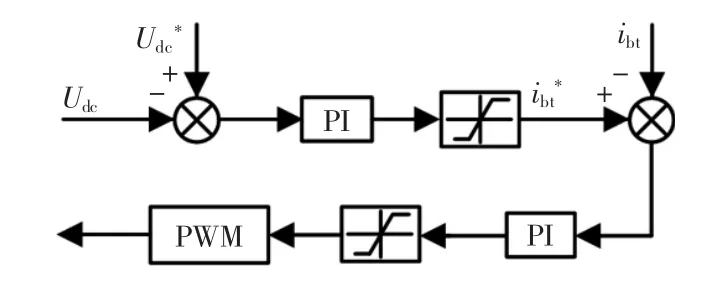
图3 蓄电池控制原理Fig.3 Battery control schematic

3 仿真结果

为验证所提出控制策略的有效性，利用MatLab/Simulink 建立了基于滑模控制的光伏电池MPPT、蓄电池储能以及微源逆变器仿真模型，其中PV 参数见表1。

表1 PV 参数Tab.1 PV parameters

根据搭建的仿真模型，设置环境温度为25℃。仿真时间0～2 s时，光照强度为420 W/m2；2～4 s时，光照强度为450 W/m2；4～6 s时，光照强度为410 W/m2；6～8 s时，光照强度为380 W/m2；8～10 s时，光照强度为420 W/m2，PV输出电流及功率波形如图4所示，Boost变流器输出功率及电压波形如图5所示。

由图4，图5可见，当环境温度保持不变，而光照辐射强度变化时，PV输出电流波动较大，符合光伏电池的输出特性，随着光照辐射强度增加，PV的最大功率点跟随增加光照辐射强度。Boost变流器输出功率、电压均跟随PV输出功率变化。

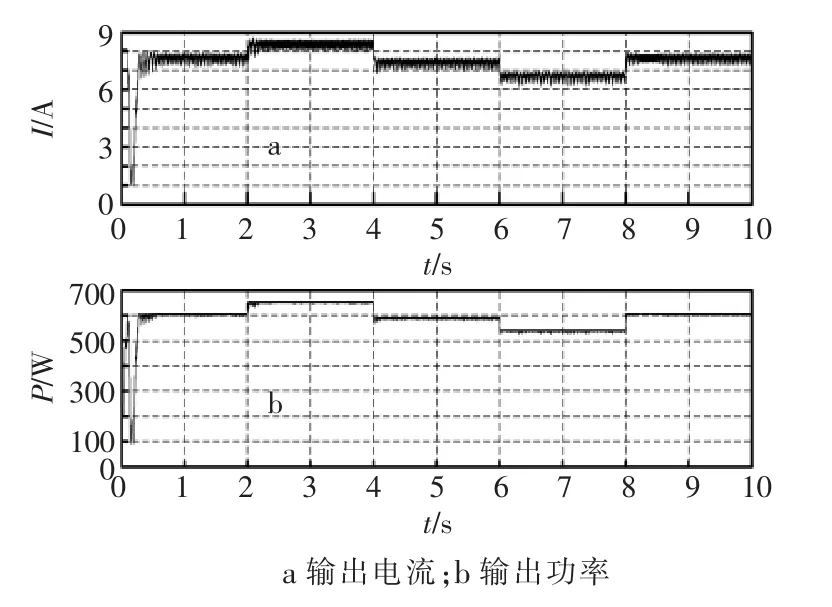
图4 PV输出电流及功率的波形Fig.4 Waveform of PV output current and power

图5 Boost输出功率及电压的波形Fig.5 Waveform of Boost output power and voltage

将3 组PV 电池串联组成PV 发电单元，通过逆变器输出，采用储能补偿后的光伏微源直流链电压波形如图6所示，由图可见，在光照条件变化的情况下，直流链电压幅值波动较小，输出电压稳定，表明该控制策略能够达到良好的直流链电压稳定控制效果。

图6 逆变器输入侧电压波形Fig.6 Voltage waveform at input side of inverte

负载从28 Ω变化至20 Ω时，系统的电压、电流波形如图7所示，图中，时间为2 s时，负载增大，系统线电压减小，1个工频周期后电压恢复。可见系统电流在负载变化时发生突变，电流增大。

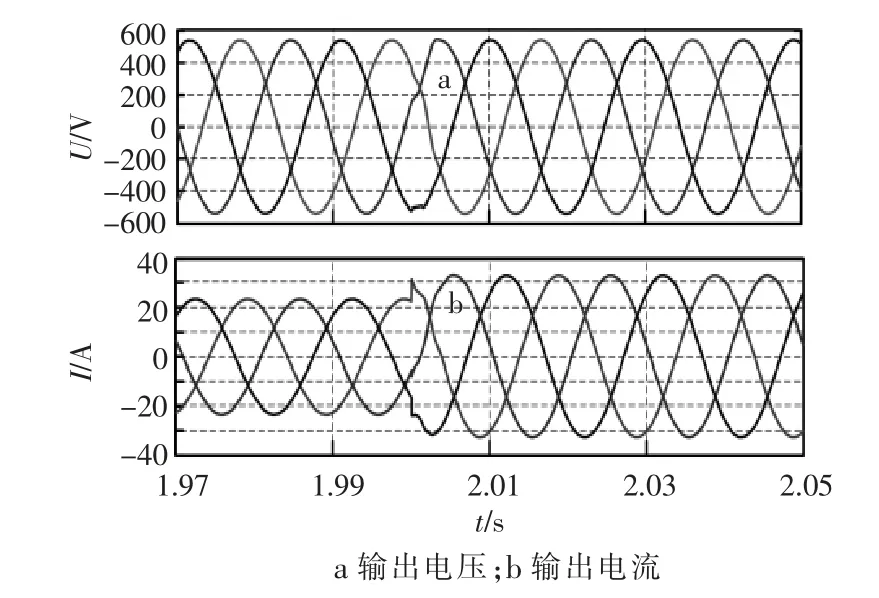
图7 系统输出电压及电流的波形Fig.7 Waveform of system output voltage and current

系统输出频率波形如图8所示，由图可见，在负载突变情况下，系统输出频率偏差始终保持在-0.2～0.2 Hz 以内，满足电网频率要求。

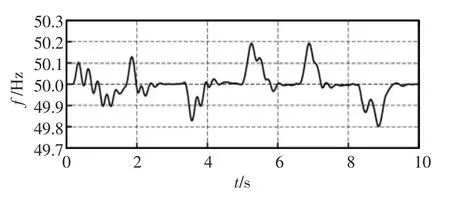
图8 系统频率波形Fig.8 System frequency waveform

4 结语

所提出的基于滑模控制和电压电流双闭环控制的独立光伏发电系统运行策略，经过仿真验证，表明：基于滑模变结构的MPPT控制器能够在光照辐射强度变化条件下快速跟踪最大功率，控制效率较高，提高了光伏微源利用率；采用蓄电池储能装置可有效抑制光伏微源输出功率随机性引起的逆变器输入侧直流母线电压波动；系统逆变器采用电压电流双闭环控制可确保在负载波动条件下系统输出电压和频率的稳定。