基于非局部均值去噪和快速谱相关的滚动轴承早期故障诊断方法

万书亭，彭勃

(华北电力大学机械工程系，河北保定，071003)

滚动轴承作为旋转机械的重要“关节”，是机械系统的重要零部件之一，当其出现故障时会影响到整个设备的安全运行[1-4]。滚动轴承早期故障时，传感器采集到的振动信号冲击分量较弱，经常被强背景噪声淹没，给诊断过程带来了难度。滚动轴承早期故障诊断一直是研究人员和学者们关注的焦点和难点。小波变换[5]、盲源分离[6]和经验模态分解[7]等分解重构方法虽然能够有效地分离噪声和原始信号，但也会导致信号局部信息失真和细节丢失。BUADES等[8]利用信号的自相似性提出了用于图像去噪的非局部均值(NLM)算法。TRACEY 等[9]和胡新海等[10]应用NLM 算法分别处理ECG 信号和地震信号，去噪后的信号均具有较大的信噪比。LÜ等[11]在经典NLM算法的基础上提出了一维NLM 快速算法，并与包络谱分析法相结合，成功提取出滚动轴承故障特征。VAN 等[12]将NLM，EMD 和包络检测相结合，利用NLM 算法首先对原始信号进行去噪处理降低背景噪声，然后利用EMD 将去噪信号分解为有限个本征模态分量(IMF)，最后对第一个IMF 分量进行包络谱分析，提取滚动轴承故障特征。熊国良等[13]将NLM和谱峭度(SK)相结合，首先利用SK算法对原始信号进行分析，并据此构造出带通滤波器实现初步降噪，然后应用NLM 算法进一步去除带内噪声，最后从滤波信号的包络谱中提取故障特征频率。滚动轴承表面局部缺陷产生的周期性冲击使其振动信号具有循环平稳特征，将循环平稳理论应用于轴承故障诊断领域[14-16]。谱相关分析方法是最有效的基于循环平稳理论的方法之一。与经典的谱分析方法不同，谱相关可以增强分析信号中蕴含的周期性成分。平均周期图(ACP)是轴承故障检测中广泛使用的谱相关估计方法[17]。周徐宁等[18]将ACP 与隐马尔可夫模型相结合实现了滚动轴承故障诊断。ANTONI等[19-20]对有关轴承信号的谱相关技术进行了研究，针对传统谱相关技术计算效率较低的问题提出了快速谱相关(FSC)方法。针对如何抑制滚动轴承早期故障振动信号中噪声和谐波干扰，增强并提取微弱故障特征，本文作者首先利用NLM 算法处理原始振动信号，降低背景噪声。然后，对降噪信号进行快速谱相关分析，增强信号中的周期成分，获得快速谱相关谱及其对应的增强包络谱。最后，识别增强包络谱中幅值突出的频率成分，准确判断故障类型。通过对仿真故障信号、实验故障信号进行分析，验证了本文提出方法的有效性。

1 理论背景

1.1 非局部均值去噪

自然图像中存在大量的类似成分，基于加权平均法搜寻类似成分去除随机噪声的NLM 算法被提出[11]。因NLM 算法可以有效保留信号中的细节信息和尖锐边缘，被用于解决一维信号处理问题。假设1个一维信号x(t)被1个高斯白噪声信号n(t)污染，则含噪声信号为

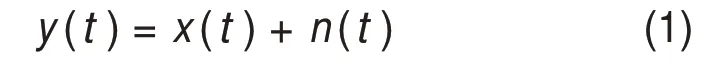
NLM算法是通过计算y(t)中全部相似块的加权平均(t)对原始x(t)进行估计进而实现去噪。(t)的计算过程如下：

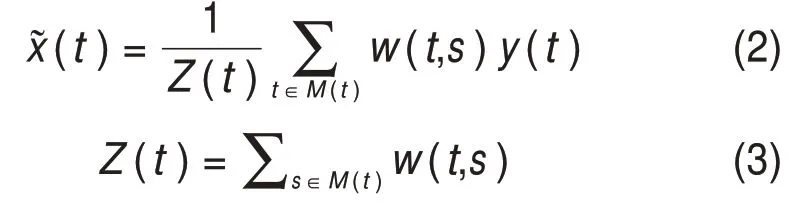
式中：w(s,t)为以t和s为中心的2 个搜索块之间的相似度；t为以点t为中心的搜索块；M(t)为搜索域中全部点的集合；Z(t)为归一化常数，表示全部搜索块相似度之和。w(s,t)需要满足如下2个条件：

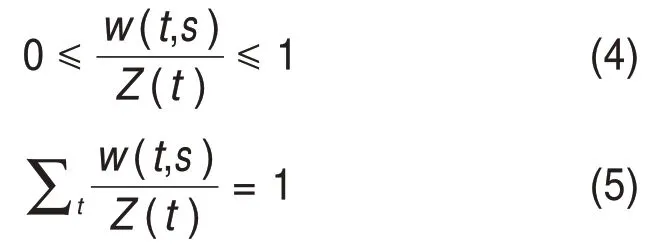
w(s,t)的计算过程如下：

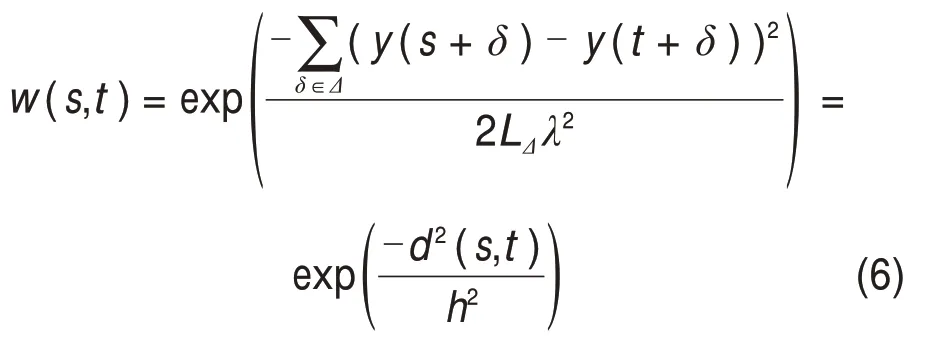
式中：λ为滤波器带宽参数；Δ为以t为中心的搜索块；LΔ为以s为中心的搜索块；d2(s,t)为以t和s为中心的2个搜索块之间欧氏距离的平方和，其数值越小，表示相似度越大；d2决定w(s,t)的衰减速度，进而控制滤波器的性能。

1.2 快速谱相关

FSC算法是由ANTONI等[20]提出的，其可以降低计算谱相关的时间且不影响效率。假设x(tn)是一个循环平稳信号，其谱相关性定义为

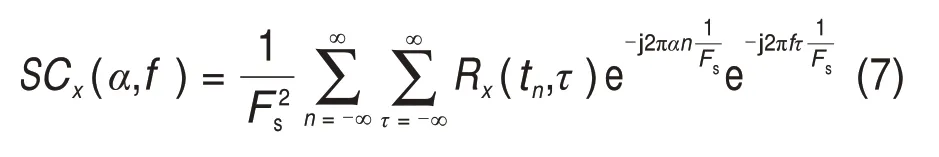
式中：Fs为采样频率；tn为时间瞬间，tn=n/Fs；Rx(tn,τ)为x(tn)的循环自相关函数；τ为时间延迟；α为循环频率；f为信号频率。谱相关是2 个频率变量的二维傅里叶变换，反映了信号相对于频率和循环频率的功率分布。

为了提高计算谱相关效率，引入短时傅里叶变换。信号x(tn)的短时傅里叶变换(STFT)分析过程如下：

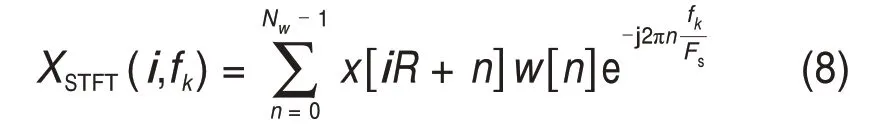
式中：Nw为STFT的窗长；R为STFT 中的块移位；w(n)为窗函数；x[n]为x(tn)的缩写形式；fk为离散频率，fk=kΔf，k=1,2,…,Nw-1；Δf为频率分辨率，Δf=Fs/Nw。

STFT的相位校正过程如下：

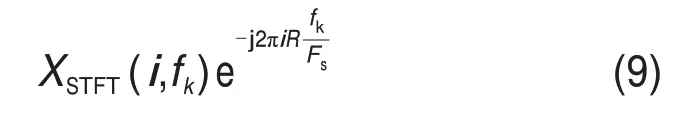
式中：Xw(i,fk)为信号x(tn)在iR/Fs处的复包络；|Xw(i,fk)|2为频带的能量流。

基于STFT的循环谱计算过程为

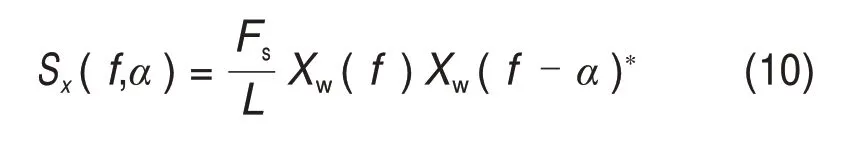
式中：L为信号x(tn)的长度。

假设f=fk=kΔf和α=pΔf+δ，可以推断f-α=fk-α≈fk-p和α≈pΔf。基于此，式(3)可以写为

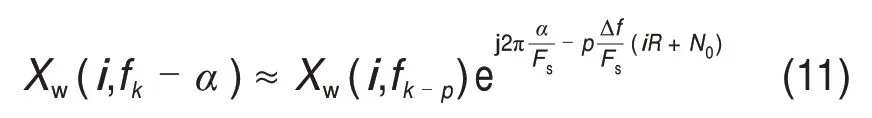
式中：p为最接近给定循环频率α的STFT 频率指数；δ为余数。

将式(11)和式(9)代入式(10)，得：

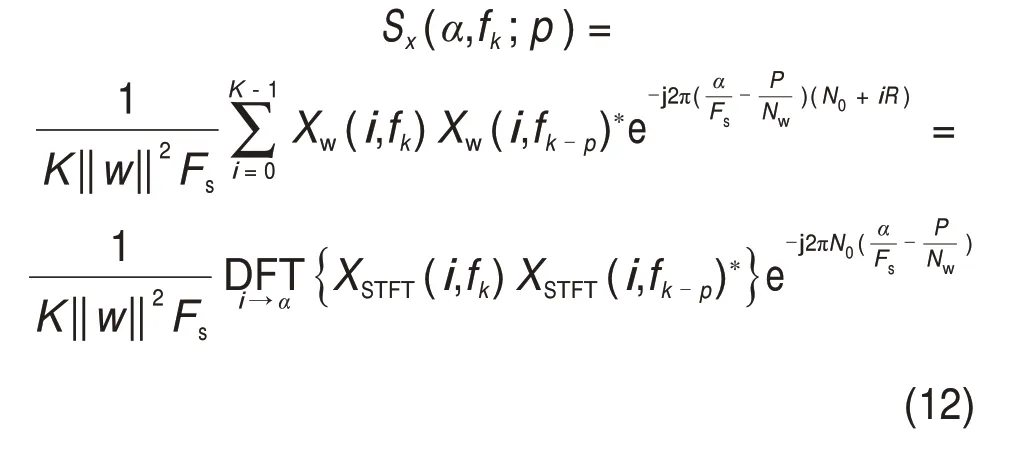
式中：DFT表示离散傅里叶变换。

当p=0 时，信号x(tn)的周期为T，其循环频率α=1/T，能量在频带[fk-Δf/2,fk+Δf/2]内周期性流动；当p≠0 时，Xw(i,fk)Xw(i,fk-p)*表示能量在频带[fk-Δf/2,fk+Δf/2]与频带[fk-p-Δf/2,fk-p+Δf/2]之间流动。

快速谱相关的定义为：

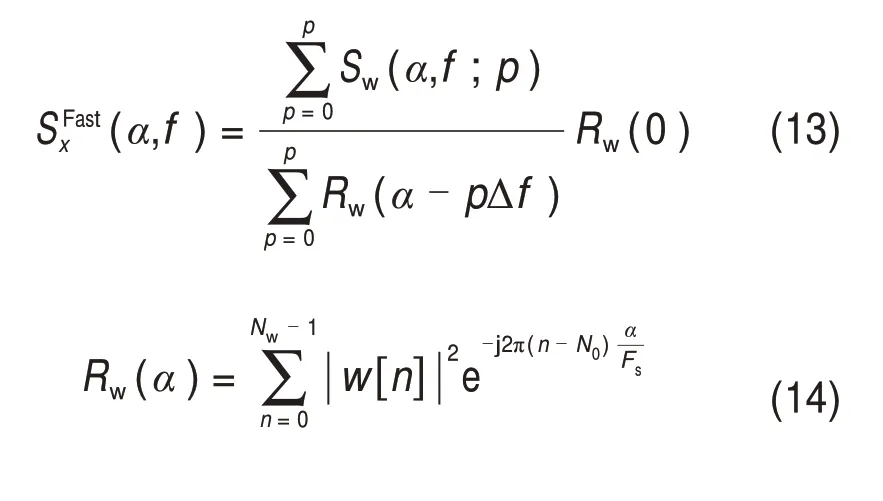
式中：Rw(α)为核函数；Rx(0)=||w||2。

快速谱相关函数定义为

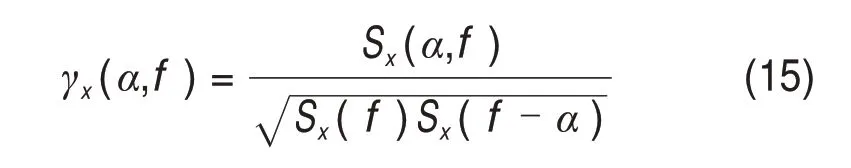
增强包络谱定义为

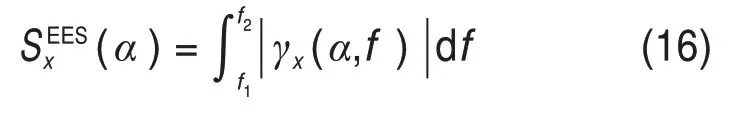
2 基于NLM-FSC 的滚动轴承早期故障诊断

NLM 算法具有良好的提高信号信噪比性能，FSC算法具有增强信号中周期成分的特性，本文提出了基于NLM-FSC 的滚动轴承早期故障诊断方法，诊断过程如图1所示。

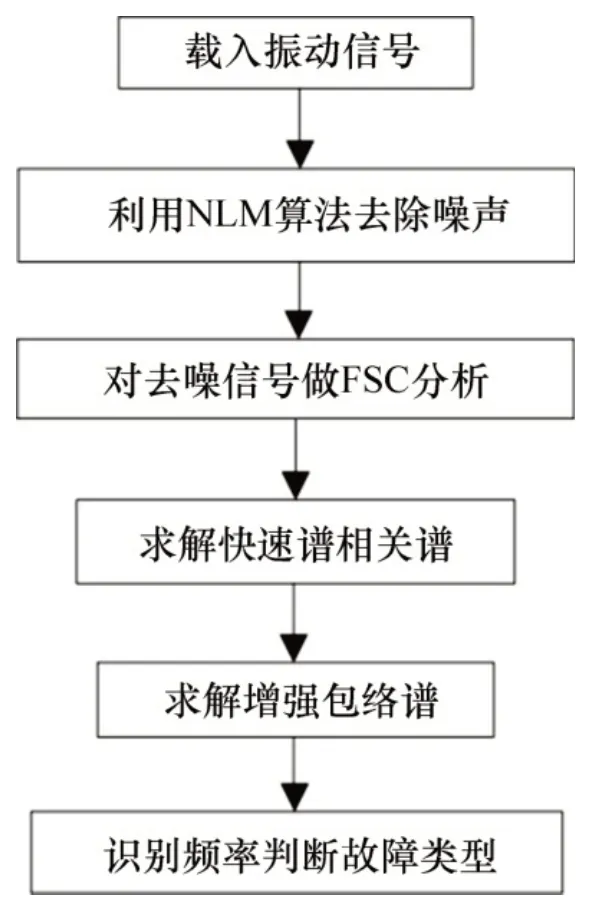
图1 NLM-FSC方法诊断流程图Fig.1 Diagnostic flow chart of NLM-FSC method

3 仿真信号分析

采用滚动轴承故障模型[21]叠加高斯白噪声的方式来仿真内圈早期故障，数学模型如下：

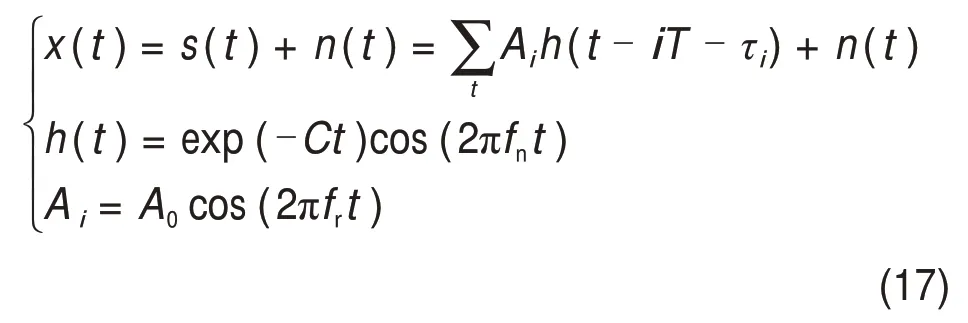
式中：s(t)为内圈缺陷产生的周期性冲击分量；n(t)为高斯白噪声；A0为信号振幅；fn为系统共振频率；fr为轴转动频率；τi为第i次冲击相对于冲击周期T的波动，且服从μ=0，σ2=0.5%×fr的正态分布；fi为内圈故障特征频率，且fi=1/T；C为系统衰减系数。仿真信号所需参数如表1所示。表1中Fs为信号的采样频率；N为信号为采样点数。仿真信号的信噪比(SNR)为-12 dB。

表1 内圈故障仿真信号参数Table 1 Parameter of inner race fault simulation signal

图2(a)所示为滚动轴承内圈早期故障仿真信号的时域波形。从图2(a)可见；周期性冲击分量被强噪声掩盖，不能观察到故障信息。对仿真信号进行包络解调，图2(b)所示为仿真信号的包络谱。从图2(b)可见有3 倍的内圈故障频率(3fi)的谐波出现。

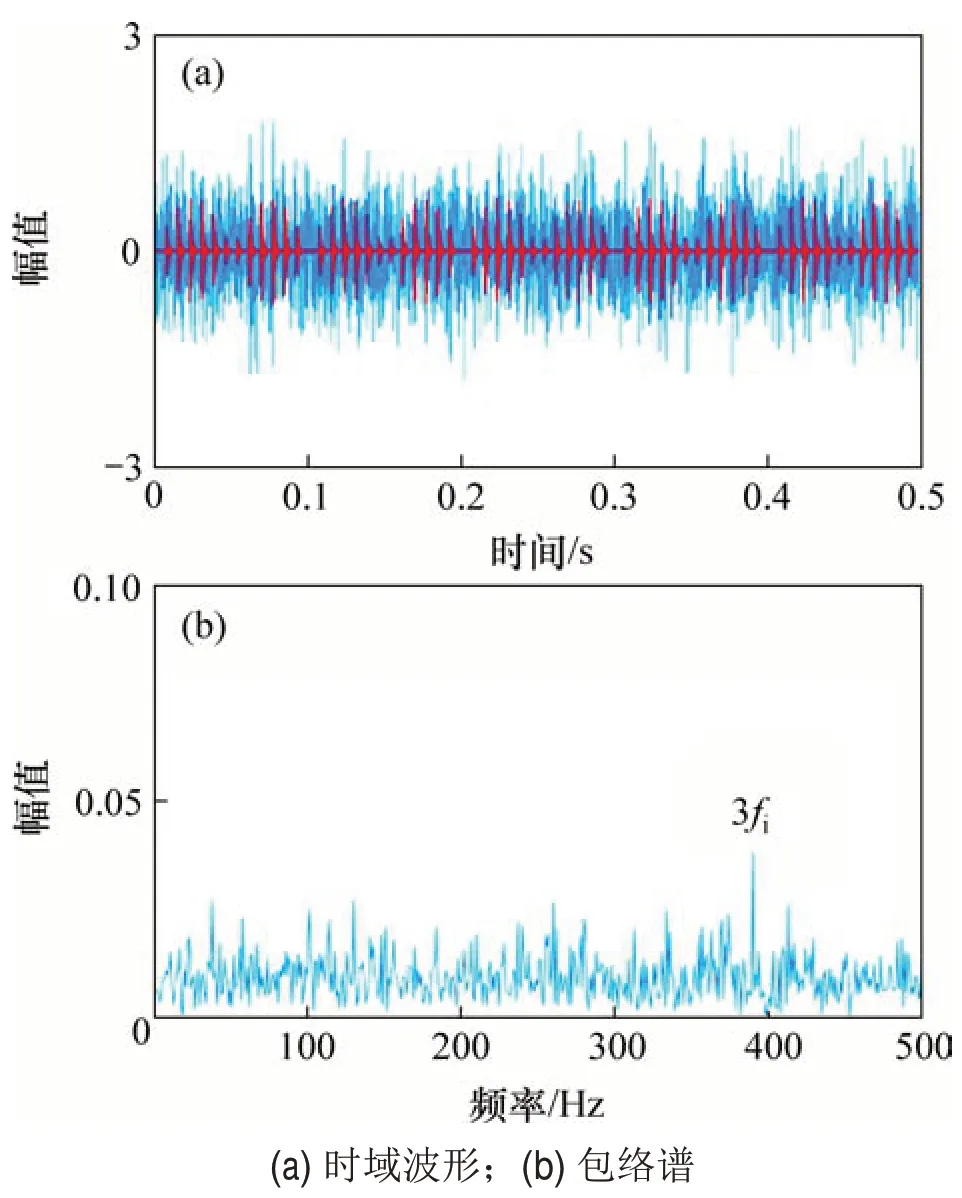
图2 仿真信号时域波形及其包络谱Fig.2 Time domain waveform and envelope spectrum of simulation signal

使用本文方法对仿真信号进行分析。首先，对故障信号进行NLM去噪，去噪后信号时域波形如图3(a)所示。然后，对去噪后信号进行快速谱相关分析，图3(b)所示为去噪信号的快速谱相关谱，在故障特征频率处出现明显的能量集中。图3(c)所示为相关谱对应的增强包络谱，有明显的内圈故障频率(fi)及其2 倍频(2fi)和3 倍频(3fi)的谐波出现，且噪声频率被明显抑制。利用本文方法可以有效地提取信号的故障特征频率，准确判断故障为内圈故障。

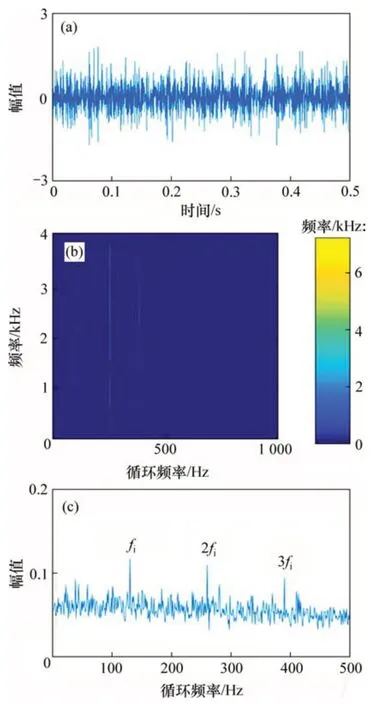
图3 本文提出方法的分析结果Fig.3 Analysis results of proposed method

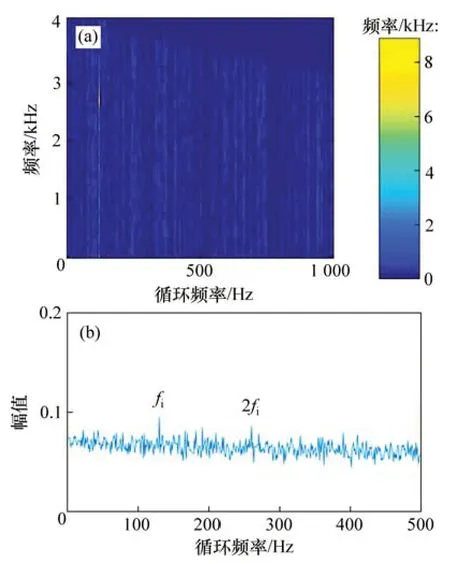
图4 快速谱相关方法的分析结果Fig.4 Analysis results of FSC method

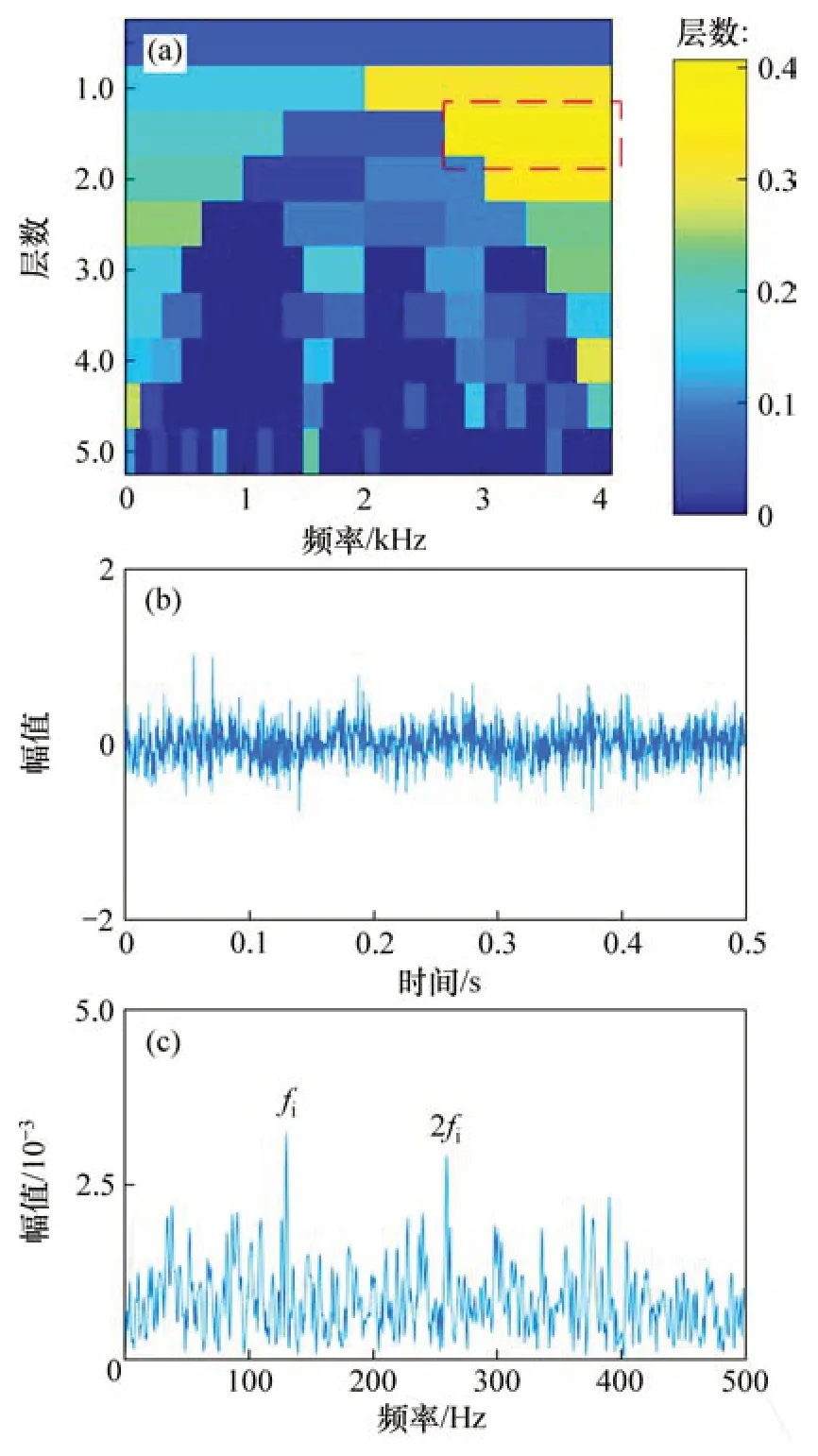
图5 SK-NLM方法的分析结果Fig.5 Analysis results of SK-NLM method

为了验证本文方法的优越性，使用快速谱相关方法，谱峭度结合非局部均值去噪方法(SKNLM)以及非局部均值去噪结合经验模态分解方法(NLM-EMD)分别对内圈故障仿真信号进行分析。图4(a)和图4(b)所示分别为仿真信号的快速谱相关谱及其对应的增强包络谱。从图4可见：内圈故障频率(fi)及其2 倍频(2fi)谐波出现，但特征频率幅值与噪声频率相比并不突出。根据文献[12]中的诊断过程，首先对仿真信号进行谱峭度分析，图5(a)所示为对应的峭度图。根据最大峭度(图5(a)中被虚线圈出)构造出中心频率为3 412 Hz、带宽为1 365 Hz的带通滤波器对仿真信号进行一次去噪。然后，利用NLM方法对信号进行二次降噪。图5(b)和图5(c)所示分别为二次去噪信号的时域波形和包络谱。从图5(b)和5(c)可见：内圈故障频率(fi)及其2 倍频(2fi)谐波出现，但噪声频率没有明显被抑制。根据文献[13]中的诊断过程，首先利用NLM 方法对信号进行降噪处理，结果如图6(a)所示。然后，利用EMD 算法分解降噪后信号得到一系列IMF 分量，选择IMF 1 分量进行包络解调分析。图6(b)和图6(c)所示分别为IMF 1分量的时域波形和包络谱。包络谱中有2 倍和3 倍的内圈故障频率(2fi和3fi)的谐波出现，但谐波幅值与噪声频率幅值接近，容易被误诊为噪声。上述分析结果表明：相较于FSC方法、SK-NLM 方法以及NLM-EMD 方法，本文方法可以抑制噪声干扰，有效提取故障特征，准确诊断故障类型。

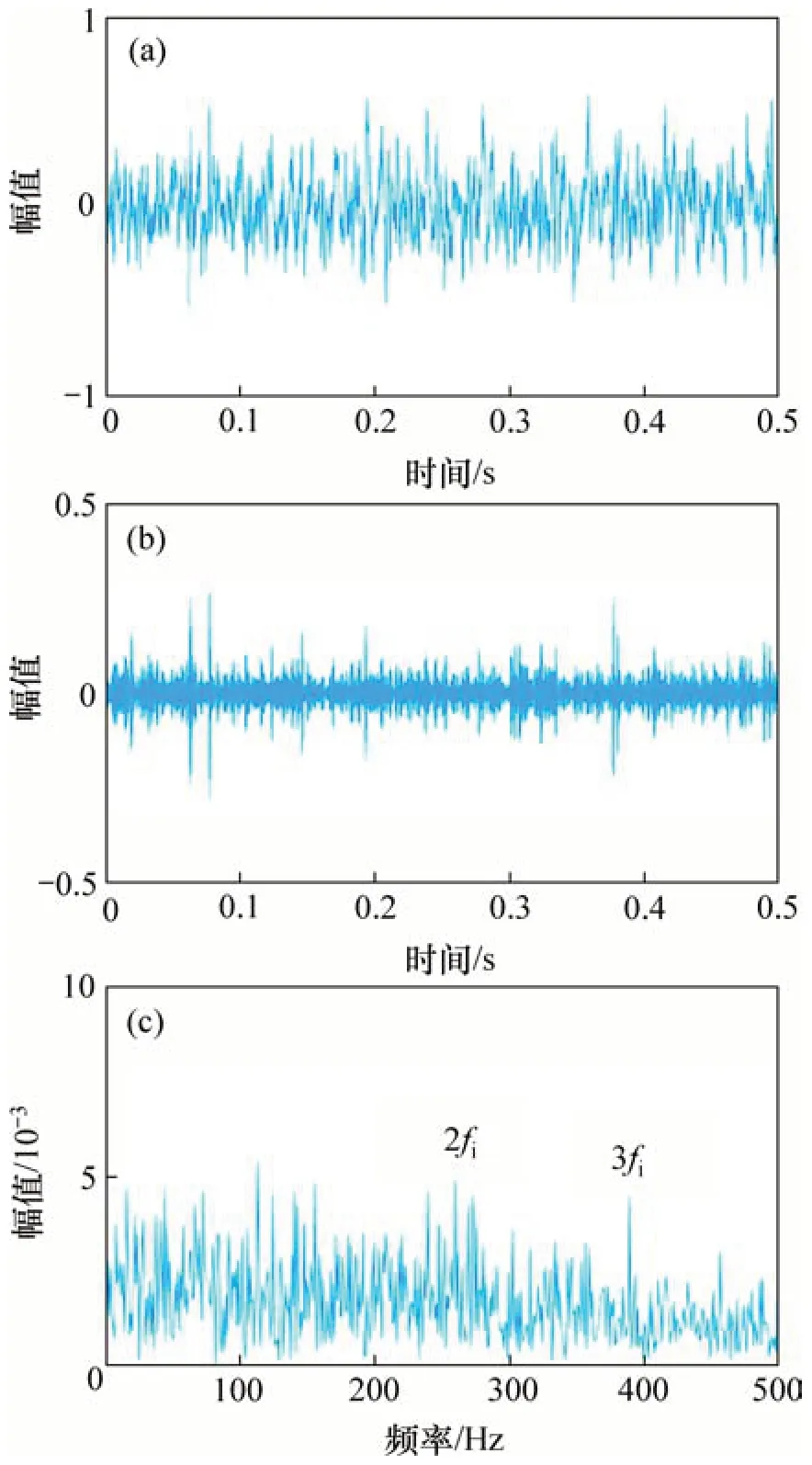
图6 NLM-EMD方法的分析结果Fig.6 Analysis results of NLM-EMD method

4 实验信号分析

为进一步说明本文方法在实际应用中的可行性，在QPZZ-II 型旋转机械故障试验台上开展了滚动轴承外圈微弱故障实验[22]。图7所示为实验台的整体外观。从图7可见：旋转轴通过联轴器和皮带轮与驱动电机连接。压力加载装置和转子盘固定在旋转轴上。正常轴承固定在左侧轴承座上，故障轴承固定在右侧轴承座上。实验对象为SKF 6203型滚动轴承，其结构参数如表2所示。采用线切割技术在外环上加工出宽度为0.1 mm、深度为0.2 mm 的凹槽，模拟滚动轴承的外圈微弱故障，如图8所示。传感器固定在右轴承座上，采集振动信号。实验时，驱动电机转频fr为24 Hz，采样频率fs为12.8 kHz。将表2所示参数和轴转频代入式(18)，计算得到外圈故障特征频率fo≈88 Hz。

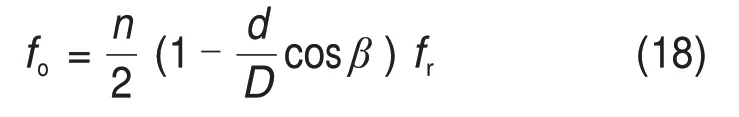
式中：n为滚动体个数；d为滚动体直径；D为节圆直径；β为接触角。

图7 QPZZ-II型实验平台Fig.7 QPZZ-II experiment platform

表2 SKF 6203型轴承结构参数Table 2 Bearing structure parameter of SKF 6203

图8 轴承外圈故障Fig.8 Bearing outer race fault

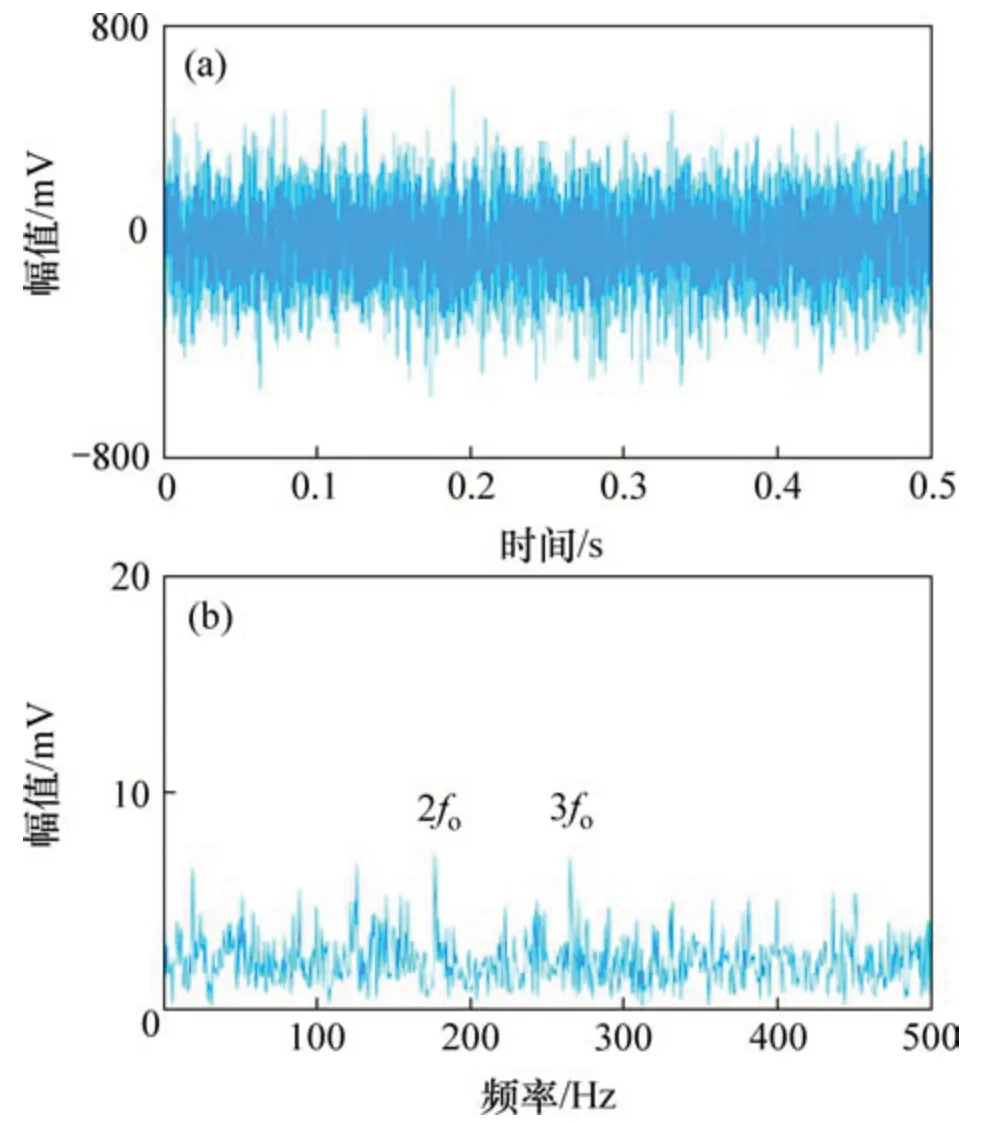
图9 实验信号时域波形及其包络谱Fig.9 Time domain waveform and envelope spectrum of experiment signal

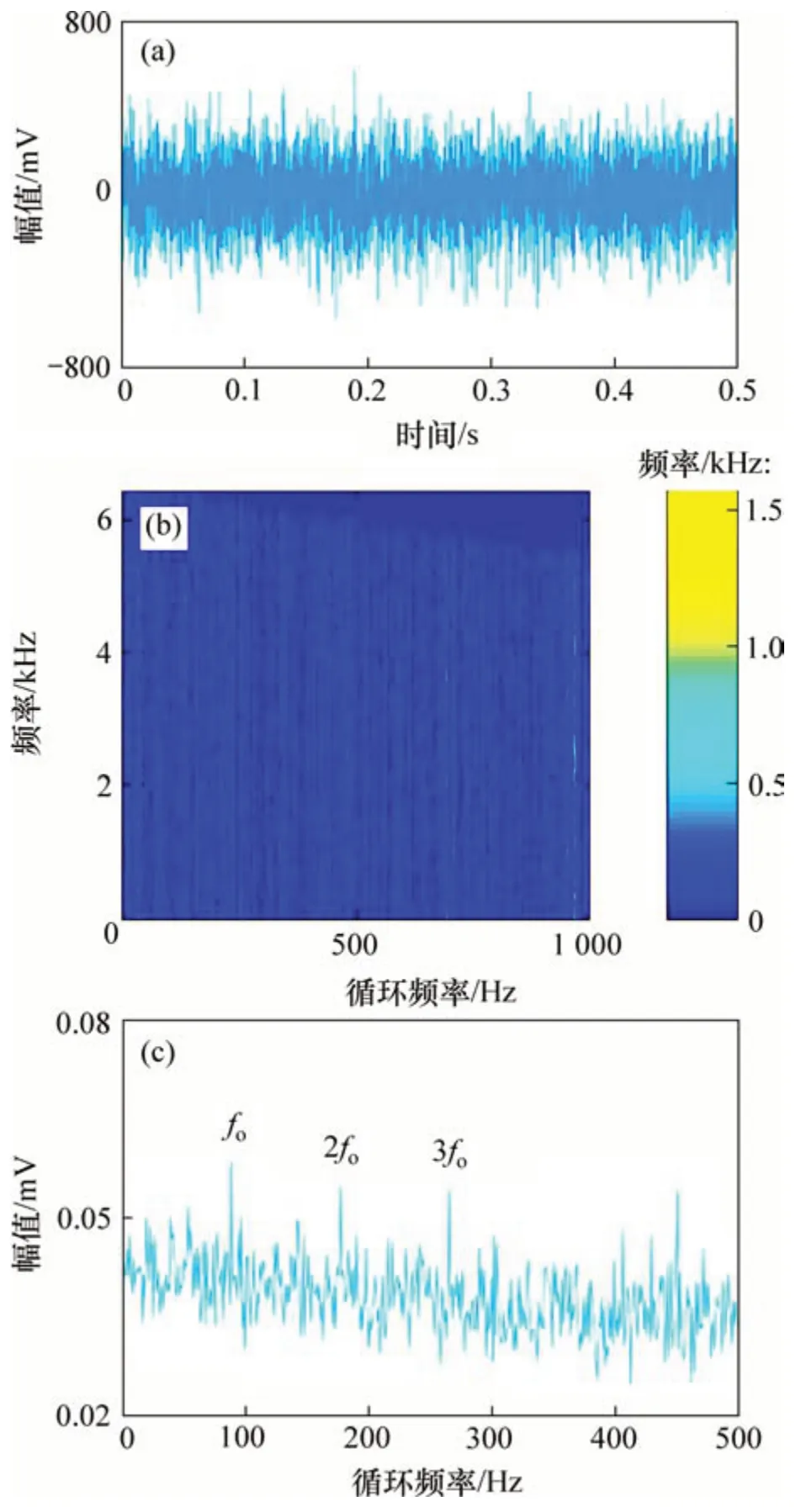
图10 本文提出方法的分析结果Fig.10 Analysis results of proposed method

图9(a)和9(b)所示分别为实验采集的振动信号时域波形及其包络谱。包络谱中有2倍和3倍的外圈故障频率(2fo和3fo)的谐波出现，但谐波幅值不突出，容易误诊为噪声频率。使用本文方法对实验信号进行分析。图10(a)，(b)和(c)所示分别为NLM去噪后信号时域波形、去噪信号的快速谱相关谱以及相关谱对应的增强包络谱。由图10(c)可知：外圈故障频率(fo)、2 倍频(2fo)和3 倍频(3fo)的谐波被有效提取，且幅值突出不会被误诊为噪声频率。分别使用FSC 方法，SK-NLM 方法以及NLMEMD 方法对实验信号进行分析，说明本文方法的优越性，图11、图12和图13所示分别为FSC 方法、SK-NLM方法和NLM-EMD方法的分析结果。由图11(b)可知：FSC方法可以提取出2倍和3倍的外圈故障频率(2fo和3fo)的谐波，但特征频率幅值与噪声频率相比并不突出，容易导致误诊。由图12(c)和图13(c)可知：SK-NLM方法和NLM-EMD方法无法提取出外圈故障频率及其谐波。经分析可知：造成SK-NLM 方法无法提取故障特征是由于谱峭度方法容易受到随机冲击噪声的干扰，构造出的带通滤波器只对随机冲击敏感，不能滤出周期冲击信号。对滤出的窄带信号进行NLM 降噪，也无法提取出故障特征(即周期冲击频率)。造成NLM-EMD方法无法提取故障特征是由于NLM算法对强噪声信号(如轴承早期故障振动信号)的处理效果不理想，加之EMD 算法自身存在模态混叠和端点效应等缺点，导致无法实现特征提取。上述分析结果表明，相较于快速谱相关方法、SKNLM方法以及NLM-EMD方法，本文方法可以抑制噪声干扰，有效提取故障特征，准确诊断故障类型。

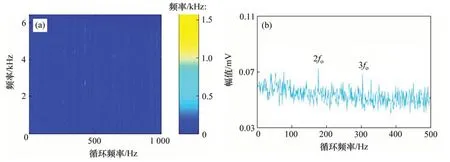
图11 快速谱相关方法的分析结果Fig.11 Analysis results of FSC method

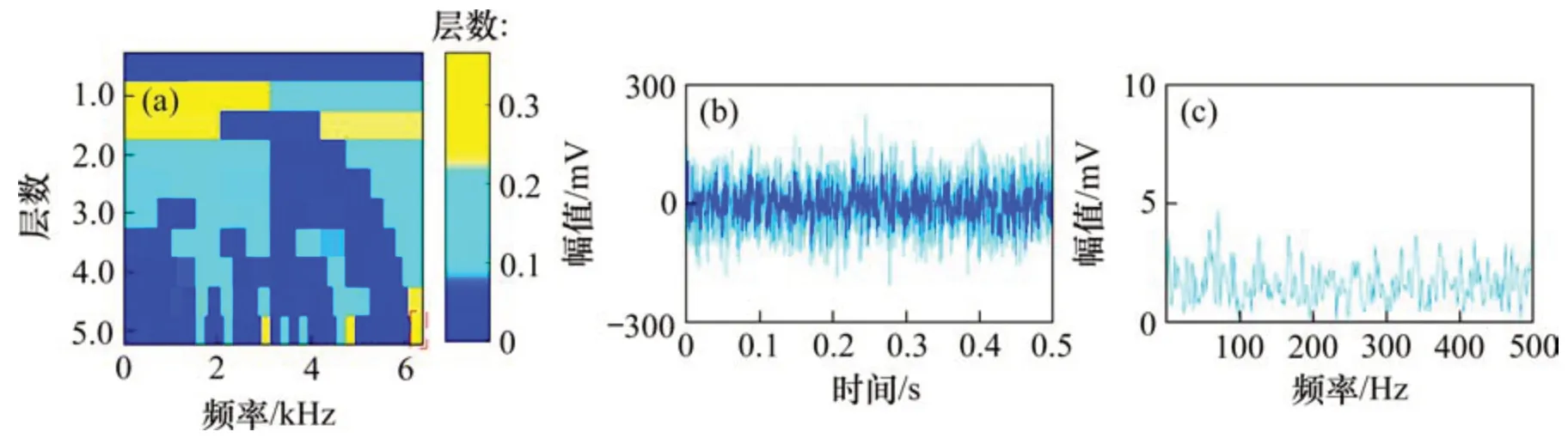
图12 SK-NLM方法的分析结果Fig.12 Analysis results of SK-NLM method

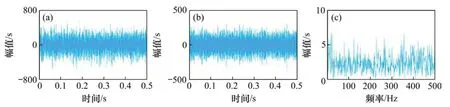
图13 NLM-EMD方法的分析结果Fig.13 Analysis results of NLM-EMD method

5 结论

1)提出基于NLM-FSC的滚动轴承早期故障诊断方法，利用非局部均值去噪算法降低噪声干扰，提高信号信噪比，结合快速谱相关算法增强信号中的周期成分，有效提取出微弱故障特征，准确判断故障类型。

2)使用本文方法对仿真故障信号、实验故障信号进行分析，结果表明所提出的方法是有效的。

3)将FSC 方法、SK-NLM 方法和NLM-EMD方法进行对比分析，结果表明所提出方法的分析效果优于直接使用FSC 方法的分析效果，并且可以避免由于SK 算法易受随机冲击噪声干扰以及NLM 算法处理信噪比低、信号效果差而造成的误诊。