考虑风电不确定性的交直流混联系统同质化能量函数模型

徐明忻，张文军，项 颂，赵 勇，党 伟，顾大可，孙 鹏

（1.国网内蒙古东部电力有限公司经济技术研究院，内蒙古 呼和浩特 010020； 2.国网内蒙古东部电力有限公司，内蒙古 呼和浩特 010020； 3.东北电力大学，吉林 吉林 132012； 4.沈阳工业大学，辽宁 沈阳 110870）

0 引言

我国已建成世界上规模最大、 电压等级最高的交直流混联电网，对国家能源资源优化配置与清洁能源消纳发挥着重要作用，是我国能源安稳运行与可持续利用的有效保障[1]～[3]。交流和直流系统控制特性不同，且发生故障后的交直流混联系统具有时空非线性时变性等特点[4]～[6]。传统以戴维南等效电路的交流系统故障分析方法不能有效评价其暂态过程，寻求新的故障分析方法及暂态评估方法已成为当务之急。 对于含大规模风电的交直流混联电网，当其交流通道或直流通道发生严重暂态故障时，亦会使风电通道功率发生大范围波动，导致整个交直流混联系统产生稳定性问题。因此，须要深入研究含大规模风电的交直流系统的同质化能量函数及稳定性判据。

在保证大规模风火打捆经交直流混合通道送出的送端电力系统安全可靠运行的条件中，交直流混合输电通道稳定性是最重要的指标之一，而直流系统与交流系统间对电网状态变化的响应时间尺度不同，也是交直流系统间稳定影响机理研究的主要问题[7]～[9]。由于交直流混合系统包含直流系统和交流系统的耦合作用，因此交直流混合系统的稳定性问题相较单独的交流系统也更加复杂和突出。

特高压交直流输电可实现大规模、长距离、大容量的能量传输和跨区域异步组网。 随着特高压交直流电网在整个电力系统中所占比例的增加，研究直流电网对整个输电系统的影响，实现对整个交直流系统可靠性的快速评估和薄弱环节判别显得尤为重要。

近年来，研究人员对特高压电网的安全稳定及稳定性评估的关注度逐渐提升。 文献[10]研究了双12 脉冲超高压直流输电系统的稳定性评估模型，但未全面考虑交流系统的影响。文献[11]对比了特高压交流和特高压直流输电的可靠性和经济性，为交直流混合系统规划的安稳约束提供了参考。 文献[12]研究了特高压主网架下全部电压等级的电力网络的稳定性评估，但其在可靠性评估指标方面未对特高压交直流系统建立较为全面模型。 截至目前，特高压交流直流混合系统可靠性评估还没有较为成熟全面的指标体系和评估方法。

本文以交直流混联系统实现风电外送的实际工程为例，提出考虑风电不确定性的交直流混联系统同质化能量模型。 在含大规模风电的交直流混联弱送端系统潮流方程基础上，研究并建立含风电的交直流混联系统支路暂态势能函数。 研究交直流混联系统功角稳定机理，建立惯量坐标下交直流同质化能量函数模型。 在此基础上，建立基于同质化能量函数的电力系统稳定性鲁棒评估模型，提出交直流混联系统稳定性判据。 算例仿真表明，本文所提模型可以有效地识别出影响电网运行稳定的薄弱环节，为含大规模新能源的交直流混联系统的稳定性控制提供理论依据。

1 交直流混联电力系统潮流方程

在交直流混联系统中，依据交流节点是否与换流器相连接的原则可将交流节点分为两类，分别为纯交流节点和交流换流器节点[13]～[15]。 在稳态计算的过程中，后者不仅须要考虑与其相连接的换流器类型与控制方式，还须要考虑换流器的有功和无功。

交直流联合电力系统潮流方程为

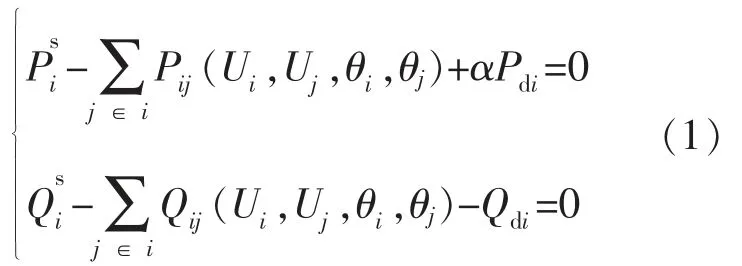
直流输电线路功率约束方程为

式中：PdR为直流输电线路功率；Id为直流输电线路电流；R 为所在线路的电阻。

含风电接入的交直流混联电力系统潮流约束如下所述：

式中：Pm，G和 Qm，G分别为节点 m 上发电机组发出的有功和无功表示机组 i 与节点 m 相连；Pm，D和 Qm，D分别为节点 m 上的有功负荷和无功负荷和 Qm，L分别为节点 i 上电容器和电抗器输入的无功功率；Um和Un分别为节点m，n 的电压幅值；θmn为节点 m，n 的相角差；Gmn为连接节点 m 的支路电导；Bmn为连接节点 m，n 的支路电纳；Pm，W和 Qm，W分别为风电场在节点 m 上的有功出力和无功出力；Udk，Idk，φk分别为与节点m 相连接的线路的电压、电流、功率因数。

如果以节点m 与线路整流侧相连为前提，那么线路 k 直流侧的电压 Ud1，k和电流 Id1，k满足 Udk=Ud1，k，Idk=Id1，k；如果以节点 m 与线路逆变侧相连为前提，那么线路 k 逆变侧的电压 Ud2，k和电流 Id2，k满足 Udk=Ud2，k，Idk=Id2，k。

Pm，W和 Qm，W可由下式确定：

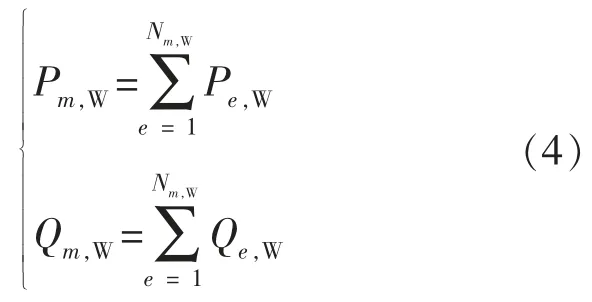
式中：Nm，W为节点 m 上的参数，指的是与该点相连接的风电机组的台数，而且这些机组并联。

Pe，W的 确 定 依 赖 于 对 风 功 率 的 预 测 ，Qe，W的值受限于变流器转子电流。

2 交直流混联系统同质化能量函数

2.1 简单模型下支路暂态势能函数

含风电的交直流混联系统如图1 所示。

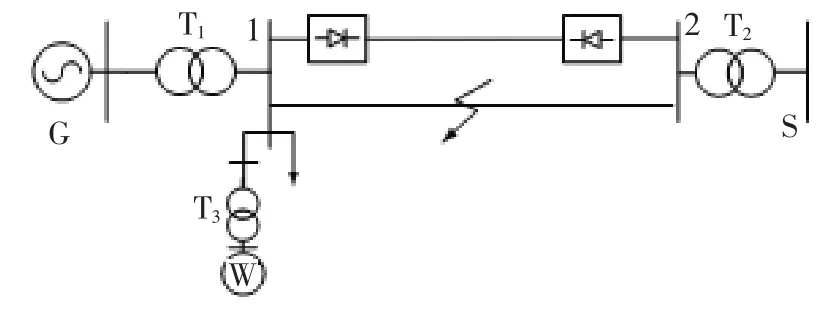
图1 含风电的混联系统Fig.1 Interconnection system with wind power

在复杂交直流混联系统中，取其中一段支路，建立简单模型下交直流混联系统支路暂态势能函数。 定义节点1 暂态势能为

式中：ω1为节点 1 角频率；P1交为节点 1 注入的同步机组交流功率；PW为风机功率；PL为负荷功率；P1直为节点 1 流入支路 1-2 的功率；PS为故障前各功率值。

此时可定义节点2 的暂态势能为

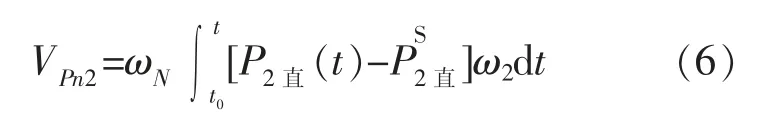
定义负荷L1的暂态势能为

定义支路2 的暂态势能为

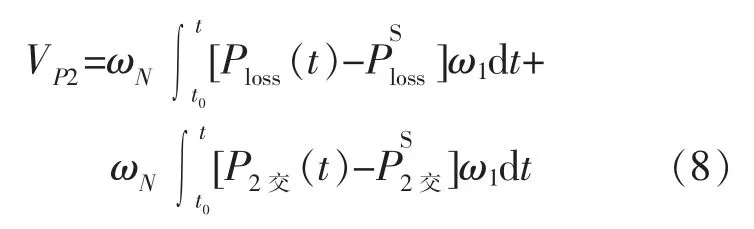
2.2 惯量坐标下的含风电交直流混联系统支路暂态能量函数数学模型

在含风电的多机交直流混联系统中，其惯量中心的等值转子角δcoi为

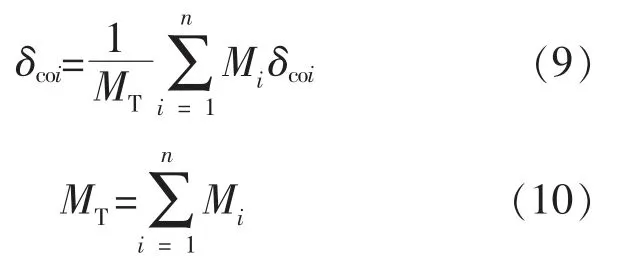
式中：Mi为各同步机的惯性时间常数。

类似的，可以得到惯量中心等值速度ωCOI：

在惯量坐标下，同步机的转角和角速度可计算如下：

对各机运动方程求和，可得系统的惯量中心运动方程：

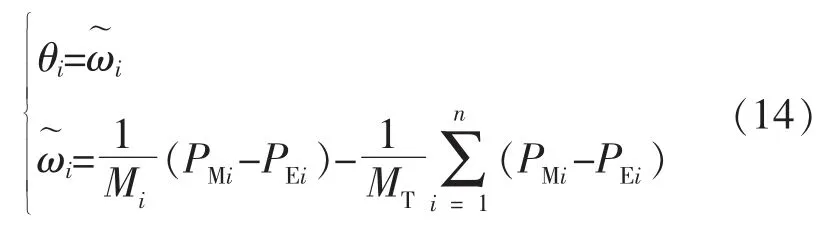
上述公式可以推广到任一节点。

2.3 改进的同质化能量函数

由同质化能量函数可知，在系统发生故障情况下，与采用同步坐标相比，采用惯量坐标时系统总动能减少了该值与负荷动能和支路电阻的动能相关。

由于电阻只与系统的有功功率相关，所以支路电阻的动能不会影响系统的稳定。因此，只有电抗的动能对系统的稳定性有决定性的影响。

另外，系统的稳定性还与各发电机是否同步有关，即与不同的发电机间角度差是否一致有关，因此，可以忽略负荷的影响。 则此时，系统的总能量为

系统的总动能为

系统的总势能为

3 基于改进暂态能量函数的电力系统稳定性评估

研究交直流混联系统的稳定性可从以下两方面进行：一是整个系统的稳定；二是局部系统的稳定。 在此基础上可从两个不同的角度进行分析：一是考虑全部支路的能量；二是考虑部分支路的能量。 当考虑全部支路的能量时，系统体现为割集的稳定。

从能量同质化的角度分析，在交直流混联系统内的动能转化为暂态势能的过程中，其割集上的输电元件可能会承受较多的暂态能量，从而产生“撕裂”现象[16]，[17]。 该割集是交直流混联系统在某一故障下最薄弱环节。 由于故障后系统暂态能量过分集中，会导致交直流混联系统失稳，因此，可将该支路及割集上暂态能量变化量作为识别系统失稳的判据。

定义临界支路指标K：支路在tc至tmk时段内的暂态能量的变化量为

式中：tc，tmk分别为系统故障切除时刻、 支路 k 首次达到最大暂态能量的时刻。

当考虑全部支路的能量时，为在判定系统稳定基础上减少计算量，可将系统支路作简化处理。 本文以交直流混联系统的拓扑树枝连接发电机的最少支路作简化。

本文通过以下方法判别交直流混联系统的临界割集。 设tm为割集的暂态能量首次达到峰值的时刻。 定义临界割集指标KCI，其为某一割集包含的所有支路暂态能量在tc～tm内增量之和：

3.1 交直流混联系统鲁棒性评估模型

研究交直流混联系统的鲁棒性，须要综合考虑交直流混联系统网络节点的连通性能，即暂态故障发生时，在一定时空范围内，系统仍可安稳运行的能力。 通过辨识网络巨簇规模，可以确定当前交直流混联系统各网络节点的连通性能。 交直流混联系统鲁棒评估式如下

式中：Kg为交直流混联系统安稳运行能力；Sc和S分别为交直流混联系统网络巨簇的节点规模和最初时刻网络正常运行的节点数；z 为交直流混联系统网络故障产生情况，取值为0 或1。

计算交直流混联系统鲁棒评估指标K，须要预先辨识暂态能量超载的节点数s 和脱离巨簇的节点数w。 负载阈值表示网络节点自身承载暂态能量限值。

节点故障的负载分配如下：

阈值系数越大的节点，可以更多地承担来自故障节点所分配的负载。根据式（22），（23）节点故障的负载分配方法，节点j 如果具有一定的暂态势能，就可以维持该节点的正常运行，即：

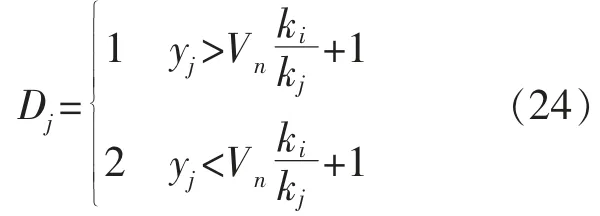
式中：Dj为 0 或 1，1 为超载；yj为阈值系数。

3.2 模型算法

为判断交直流混联系统鲁棒性，提出相应的算法进行求解。以网络节点导纳矩阵、故障概率等为输入参数，以网络鲁棒性指标Kg为输出结果。算法流程如图2 所示。

图2 算法流程图Fig.2 Algorithm flowchart

4 仿真及结果分析

图3 为4 机19 节点电力系统拓扑结构图。其中，2，3 为同步机，1，4 为风机安装节点，节点 6，9为敏感负荷，节点19 为可调负荷，节点13，14，17，18 为可中断负荷。

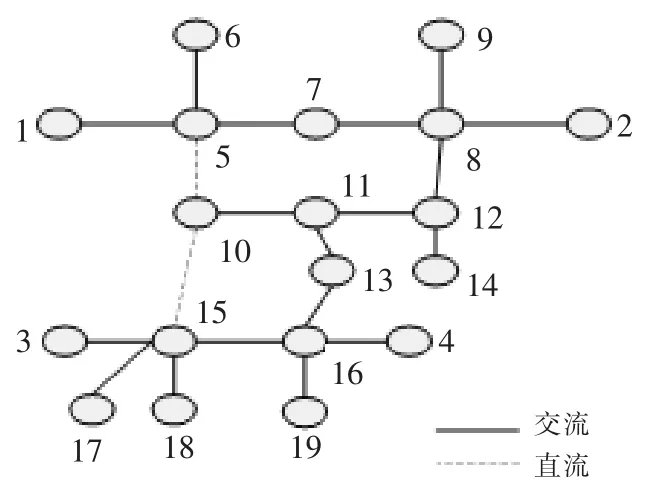
图3 4 机19 节点拓扑结构图Fig.3 4 machine 19-node topology diagram

若节点3 的同步机出口发生三相瞬时性短路，故障切除时间 t 分别为 0.10，0.20，0.30 s，计算各临界支路指标K 如表1 所示。

表1 临界支路指标Table 1 Critical branch indicators

从表1 可见，支路 16-19，15-16 指标 K 较大，且随故障时间的增加而增加，支路16-19，15-16 为发生故障时较薄弱的支路。距离故障点附近割集的KCI如表2 所示。

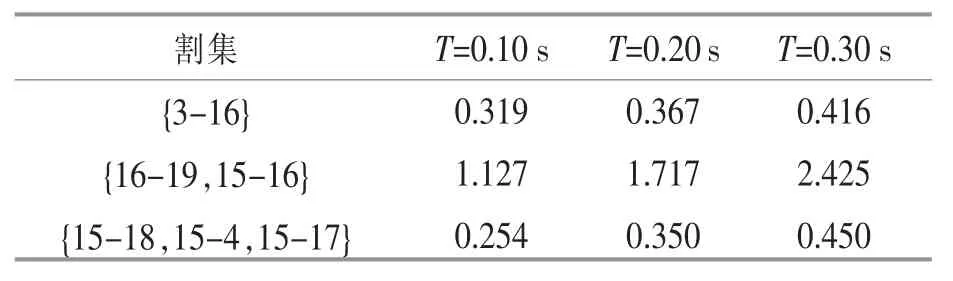
表2 临界割集指标Table 2 Critical cut set indicators

由表2 可以看出，割集{16-19，15-16}的指标KCI随系统故障时间增加而增大，即割集在 {16-19，15-16} 失稳而撕裂开，表现为暂态能量值过高，系统失稳时部分支路的电压相位差如图4 所示。 从支路 3-16，16-19，15-16，15-18，15-4，15-17 的电压相位差的变化曲线看，系统在包含支路16-19，15-16 处断裂，侧面证明了本文临界割集指标的正确性。

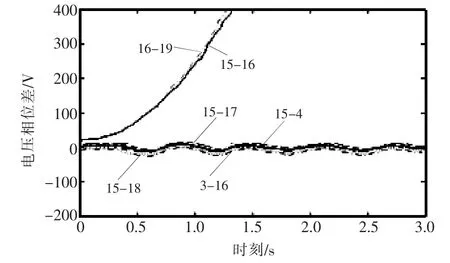
图4 系统失稳时部分支路的电压相位差Fig.4 Voltage phase difference of some branches when the system is unstable

在不同故障概率下进行鲁棒性判别。 由图5可知，故障概率与鲁棒性成反比，阈值系数与鲁棒性强弱成正比，故可从鲁棒性强弱角度分析稳定性判据。

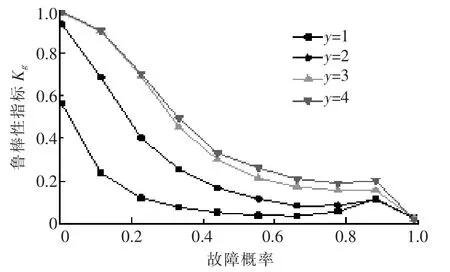
图5 节点故障时的仿真结果Fig.5 Simulation results when a node fails

5 结束语

本文以特高压交直流混联系统为背景，根据传统电力系统网络中暂态能量的变化规律，提出了在惯性中心坐标下的交直流混联系统的能量函数及混联系统的稳定性指标。 利用该函数和稳定性指标可以有效地识别出影响电网运行稳定的薄弱环节，为交直流混联系统暂态稳定评估提供新的思路和手段，为含大规模风电的交直流混联系统动态安全控制提供理论基础。